期末真题检测卷(含解析)-2024-2025学年数学七年级下册北师大版(2024)
文档属性
| 名称 | 期末真题检测卷(含解析)-2024-2025学年数学七年级下册北师大版(2024) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-05 18:13:19 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末真题检测卷-2024-2025学年数学七年级下册北师大版(2024)
一.选择题(共8小题)
1.(2024秋 滨海新区期末)考古学家们破译了玛雅人的天文历,其历法非常精确.他们计算的地球一年天数与现代相比仅差0.000069天.用科学记数法表示0.000069为( )
A.0.69×10﹣4 B.6.9×10﹣5 C.6.9×10﹣4 D.69×10﹣6
2.(2018秋 芝罘区期末)如图,一个可以自由转动的转盘被等分成6个扇形区域,并涂上了相应的颜色,转动转盘,转盘停止后,指针指向黄色区域的概率是( )
A. B. C. D.
3.(2019春 西城区期末)下列计算正确的是( )
A.a2 a3=a6 B.a8÷a2=a4
C.(a2)3=a6 D.(﹣2ab)3=﹣8a3b
4.(2024秋 禅城区期末)如图,直线m∥n,一把含30°角的直角三角尺按所示位置摆放,若∠1=30°,则∠2的度数是( )
A.20° B.25° C.30° D.40°
5.(2024秋 环江县期末)如图,线段AC的垂直平分线交AB于点D,∠A=48°,则∠BDC的度数为( )
A.48° B.96° C.90° D.84°
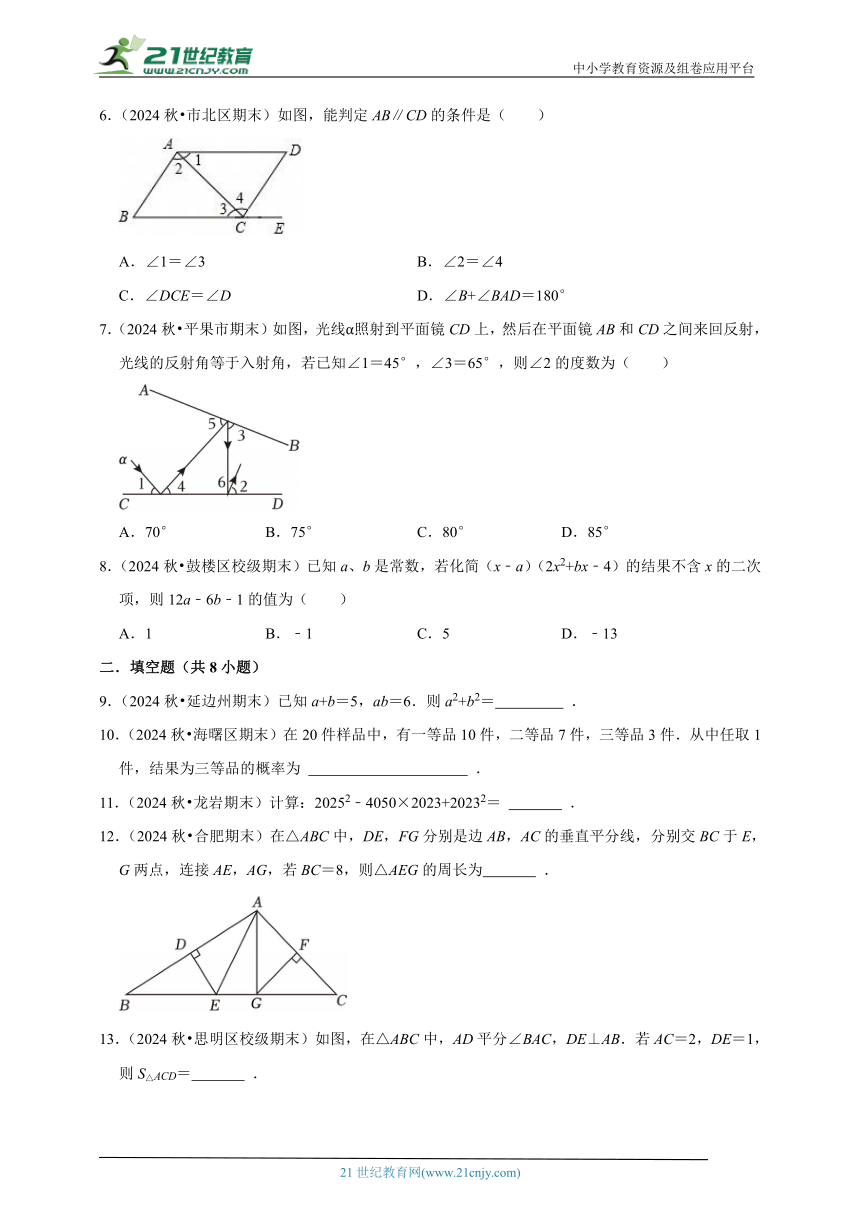
6.(2024秋 市北区期末)如图,能判定AB∥CD的条件是( )
A.∠1=∠3 B.∠2=∠4
C.∠DCE=∠D D.∠B+∠BAD=180°
7.(2024秋 平果市期末)如图,光线α照射到平面镜CD上,然后在平面镜AB和CD之间来回反射,光线的反射角等于入射角,若已知∠1=45°,∠3=65°,则∠2的度数为( )
A.70° B.75° C.80° D.85°
8.(2024秋 鼓楼区校级期末)已知a、b是常数,若化简(x﹣a)(2x2+bx﹣4)的结果不含x的二次项,则12a﹣6b﹣1的值为( )
A.1 B.﹣1 C.5 D.﹣13
二.填空题(共8小题)
9.(2024秋 延边州期末)已知a+b=5,ab=6.则a2+b2= .
10.(2024秋 海曙区期末)在20件样品中,有一等品10件,二等品7件,三等品3件.从中任取1件,结果为三等品的概率为 .
11.(2024秋 龙岩期末)计算:20252﹣4050×2023+20232= .
12.(2024秋 合肥期末)在△ABC中,DE,FG分别是边AB,AC的垂直平分线,分别交BC于E,G两点,连接AE,AG,若BC=8,则△AEG的周长为 .
13.(2024秋 思明区校级期末)如图,在△ABC中,AD平分∠BAC,DE⊥AB.若AC=2,DE=1,则S△ACD= .
14.(2024春 德州期末)光从一种介质射向另一种介质时会发生折射.如图,用直线m,n表示一块玻璃的两个面,且m∥n.现有一束光线AB从空气射向玻璃,BC是折射光线,D为射线AB延长线上一点.若∠1=20°,∠2=145°,则∠3= .
15.(2024秋 高新区期末)一个盒子中装有a个白球和6个红球,这些球除颜色外完全相同,若每次将球充分搅匀后,任意摸出1个球记下颜色再放回盒子,通过大量重复试验,发现摸到白球的频率稳定在60%,估计a的值为 .
16.(2024秋 高坪区期末)如图,在Rt△ABC中,∠C=90°,分别以点A、B为圆心,大于的长为半径画弧,交于点M、N,作直线MN分别交BC、AB于点D、E,连接AD.若∠B=32°,则∠CAD的度数为 °.
三.解答题(共7小题)
17.(2024秋 延边州期末)计算:(y+2)(y﹣2)﹣(y﹣1)(y﹣3).
18.(2024秋 河南期末)如图,点D在AC边上,∠A=∠B,AE=BE,∠1=∠2.
(1)求证:△AEC≌△BED;
(2)若∠1=45°,求∠BDE的度数.
19.(2024秋 呼和浩特期末)如图,在△ABC中,点D在边BA的延长线上,过点D作射线DM∥BC,点E是射线DM上一个定点.
(1)尺规作图:在射线DM上方求作∠DEF,使得∠DEF=∠C,与BA的延长线交于点F.(不用写作图步骤,保留作图痕迹)
(2)在(1)问条件下,若BD=AF,求证:AC∥FE.
请把以下的解题过程补充完整.
证明:∵DM∥BC(已知),
∴∠B=∠FDE(① ),
∵BD=AF(已知),
∴BD﹣AD=② (等式的性质),即AB=FD,
在△ABC和△FDE中,,
∴△ABC≌△FDE(④ ),
∴⑤ (全等三角形的对应角相等),
∴AC∥FE(⑥ ).
20.(2024秋 天门期末)有些大数值问题可以通过用字母代替数转化成整式问题来解决,请先阅读下面的解题过程,再解答下面的问题.
例:若x=6789×6786,y=6788×6787,试比较x,y的大小.
解:设6788=a,
那么x=(a+1)(a﹣2)=a2﹣a﹣2,y=a(a﹣1)=a2﹣a.
因为x﹣y=(a2﹣a﹣2)﹣(a2﹣a)=﹣2<0,即x﹣y<0,所以x<y.
看完后,你学会了这种方法吗?利用上面的方法解答下列问题:
若x=2024×2028﹣2025×2027,y=2025×2029﹣2026×2028,试比较x,y的大小.
21.(2024秋 响水县期末)某商场今年国庆节期间举行有奖促销活动,凡购买一定金额的商品可参与转盘抽奖.如图,转盘分为“A”“B”“C”“D”四个区域,自由转动转盘,若指针落在字母“B”所在的区域内,则顾客中奖(转到公共线位置时重转).若某顾客转动1次转盘,求其中奖的概率.
22.(2024秋 大理州期末)如图,某小区有一块长为(3a+2b)米,宽为(2a﹣3b)米的长方形地块,角上有四个边长为b米的小正方形空地,开发商计划将阴影部分进行绿化.
(1)求该小区绿化的总面积;
(2)若a=10,b=2,绿化成本为50元/平方米,则完成绿化共需要多少钱?
23.(2024秋 高碑店市期末)已知直线AB∥CD,E为平面内一点,点P,Q分别在直线AB,CD上,连接PE,EQ.
(1)如图1,若点E在直线AB,CD之间,求证:∠PEQ=∠BPE+∠DQE.
(2)如图2,若点E在直线AB,CD之间,PF平分∠APE,QF平分∠CQE,当∠PEQ=100°时.求∠PFQ的度数.
(3)如图3,若点E在直线AB的上方,QF平分∠CQE,PH平分∠APE,PH的反向延长线交QF于点F,当∠PEQ=50°时,求∠PFQ的度数.
期末真题检测卷-2024-2025学年数学七年级下册北师大版(2024)
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 B A C C B B D B.
一.选择题(共8小题)
1.(2024秋 滨海新区期末)考古学家们破译了玛雅人的天文历,其历法非常精确.他们计算的地球一年天数与现代相比仅差0.000069天.用科学记数法表示0.000069为( )
A.0.69×10﹣4 B.6.9×10﹣5 C.6.9×10﹣4 D.69×10﹣6
【解答】解:0.000069=6.9×10﹣5;
故选:B.
2.(2018秋 芝罘区期末)如图,一个可以自由转动的转盘被等分成6个扇形区域,并涂上了相应的颜色,转动转盘,转盘停止后,指针指向黄色区域的概率是( )
A. B. C. D.
【解答】解:∵转盘被等分成6个扇形区域,
而黄色区域占其中的一个,
∴指针指向黄色区域的概率.
故选:A.
3.(2019春 西城区期末)下列计算正确的是( )
A.a2 a3=a6 B.a8÷a2=a4
C.(a2)3=a6 D.(﹣2ab)3=﹣8a3b
【解答】解:A、a2 a3=a5,故此选项错误;
B、a8÷a2=a6,故此选项错误;
C、(a2)3=a6,正确;
D、(﹣2ab)3=﹣8a3b3,故此选项错误;
故选:C.
4.(2024秋 禅城区期末)如图,直线m∥n,一把含30°角的直角三角尺按所示位置摆放,若∠1=30°,则∠2的度数是( )
A.20° B.25° C.30° D.40°
【解答】解:如图:
∵∠1=30°,∠4=90°,
∴∠DCB=∠1+∠4=120°,
∵直线m∥n,
∴∠ABC=180°﹣∠BCD=60°,
∵∠3=30°,
∴∠2=∠ABC﹣∠3=30°,
故选:C.
5.(2024秋 环江县期末)如图,线段AC的垂直平分线交AB于点D,∠A=48°,则∠BDC的度数为( )
A.48° B.96° C.90° D.84°
【解答】解:∵DE是线段AC的垂直平分线,
∴DA=DC,
∴∠DCA=∠A=48°,
∴∠BDC=∠DCA+∠A=96°,
故选:B.
6.(2024秋 市北区期末)如图,能判定AB∥CD的条件是( )
A.∠1=∠3 B.∠2=∠4
C.∠DCE=∠D D.∠B+∠BAD=180°
【解答】解:A.当∠1=∠3时,不能得到AB∥CD,故A选项错误;
B.当∠2=∠4时,能得到AB∥CD,故B选项正确;
C.当∠DCE=∠D时,不能得到AB∥CD,故C选项错误;
D.当∠B+∠BAD=180°时,不能得到AB∥CD,故D选项错误;
故选:B.
7.(2024秋 平果市期末)如图,光线α照射到平面镜CD上,然后在平面镜AB和CD之间来回反射,光线的反射角等于入射角,若已知∠1=45°,∠3=65°,则∠2的度数为( )
A.70° B.75° C.80° D.85°
【解答】解:根据题意可得,∠4=∠1=45°,∠5=∠3=65°,∠2=∠6,
由三角形内角和定理和平角的定义得∠2=180°﹣45°﹣(180°﹣65°×2)=85°;
故选:D.
8.(2024秋 鼓楼区校级期末)已知a、b是常数,若化简(x﹣a)(2x2+bx﹣4)的结果不含x的二次项,则12a﹣6b﹣1的值为( )
A.1 B.﹣1 C.5 D.﹣13
【解答】解:∵多项式(x﹣a)(2x2+bx﹣4)=2x3+(﹣2a+b)x2+(﹣ab﹣4)x+4a不含x的二次项,
∴﹣2a+b=0,
解得b=2a,
∴12a﹣6b﹣1=12a﹣6×2a﹣1=﹣1.
故选:B.
二.填空题(共8小题)
9.(2024秋 延边州期末)已知a+b=5,ab=6.则a2+b2= 13 .
【解答】解:∵a+b=5,
∴(a+b)2=25,
∴a2+2ab+b2=25.
∵ab=6,
∴a2+b2+12=25,
∴a2+b2=13.
故答案为:13.
10.(2024秋 海曙区期末)在20件样品中,有一等品10件,二等品7件,三等品3件.从中任取1件,结果为三等品的概率为 .
【解答】解:∵共20件样品,三等品有3件,
∴从中任取1件,结果为三等品的概率为,
故答案为:.
11.(2024秋 龙岩期末)计算:20252﹣4050×2023+20232= 4 .
【解答】解:原式=20252﹣2×2025×2023+20232
=(2025﹣2023)2
=22
=4.
故答案为:4.
12.(2024秋 合肥期末)在△ABC中,DE,FG分别是边AB,AC的垂直平分线,分别交BC于E,G两点,连接AE,AG,若BC=8,则△AEG的周长为 8 .
【解答】解:∵DE,FG分别是边AB,AC的垂直平分线,
∴AE=BE,AG=CG,
∴BC=BE+EG+CG=AE+EG+AG,
∴△AEG的周长=AE+EG+AG=BC=8.
故答案为:8.
13.(2024秋 思明区校级期末)如图,在△ABC中,AD平分∠BAC,DE⊥AB.若AC=2,DE=1,则S△ACD= 1 .
【解答】解:过点D作DF⊥AC,垂足为F,
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF=1,
∵AC=2,
∴S△ACDAC DF
2×1
=1,
故答案为:1.
14.(2024春 德州期末)光从一种介质射向另一种介质时会发生折射.如图,用直线m,n表示一块玻璃的两个面,且m∥n.现有一束光线AB从空气射向玻璃,BC是折射光线,D为射线AB延长线上一点.若∠1=20°,∠2=145°,则∠3= 125° .
【解答】解:∵∠2=145°,∠1=20°,
∴∠DBE=180°﹣145°=35°,
∴∠CBE=∠1+∠DBE=20°+35°=55°,
∵m∥n,
∴∠3=180°﹣55°=125°.
故答案为:125°.
15.(2024秋 高新区期末)一个盒子中装有a个白球和6个红球,这些球除颜色外完全相同,若每次将球充分搅匀后,任意摸出1个球记下颜色再放回盒子,通过大量重复试验,发现摸到白球的频率稳定在60%,估计a的值为 9 .
【解答】解:由题意可得,60%,
解得,a=9.
经检验,a=9是分式方程的解且符合题意,
故答案为:9.
16.(2024秋 高坪区期末)如图,在Rt△ABC中,∠C=90°,分别以点A、B为圆心,大于的长为半径画弧,交于点M、N,作直线MN分别交BC、AB于点D、E,连接AD.若∠B=32°,则∠CAD的度数为 26 °.
【解答】解:由作法得MN垂直平分AB,
∴AD=BD,
∴∠DAB=∠B=32°,
∵∠C=90°,
∴∠BAC=90°﹣∠B=90°﹣32°=58°,
∴∠CAD=∠BAC﹣∠BAD=58°﹣32°=26°.
故答案为:26.
三.解答题(共7小题)
17.(2024秋 延边州期末)计算:(y+2)(y﹣2)﹣(y﹣1)(y﹣3).
【解答】解:(y+2)(y﹣2)﹣(y﹣1)(y﹣3)
=y2﹣4﹣(y2﹣3y﹣y+3)
=y2﹣4﹣y2+3y+y﹣3
=4y﹣7.
18.(2024秋 河南期末)如图,点D在AC边上,∠A=∠B,AE=BE,∠1=∠2.
(1)求证:△AEC≌△BED;
(2)若∠1=45°,求∠BDE的度数.
【解答】(1)证明:∵∠1=∠2,∠2+∠BDE=∠ADE=∠1+∠C,
∴∠BDE=∠C,
在△AEC和△BED中,
,
∴△AEC≌△BED(AAS),
(2)解:∵△AEC≌△BED,
∴ED=EC,
∴∠C=∠EDC,
∵∠1=45°,
∴,
∴∠BDE=67.5°.
19.(2024秋 呼和浩特期末)如图,在△ABC中,点D在边BA的延长线上,过点D作射线DM∥BC,点E是射线DM上一个定点.
(1)尺规作图:在射线DM上方求作∠DEF,使得∠DEF=∠C,与BA的延长线交于点F.(不用写作图步骤,保留作图痕迹)
(2)在(1)问条件下,若BD=AF,求证:AC∥FE.
请把以下的解题过程补充完整.
证明:∵DM∥BC(已知),
∴∠B=∠FDE(① 两直线平行,同位角相等 ),
∵BD=AF(已知),
∴BD﹣AD=② AF﹣AD (等式的性质),即AB=FD,
在△ABC和△FDE中,,
∴△ABC≌△FDE(④ AAS ),
∴⑤ ∠BAC=∠DFE (全等三角形的对应角相等),
∴AC∥FE(⑥ 同位角相等,两直线平行 ).
【解答】(1)解:如图,∠DEF即为所求;
(2)证明:∵DM∥BC(已知),
∴∠B=∠FDE(两直线平行,同位角相等),
∵BD=AF(已知),
∴BD﹣AD=AF﹣AD(等式的性质),
∴AB=FD
在△ABC和△FDE中,
.
∴△ABC≌△FDE(AAS),
∴∠BAC=∠DFE(全等三角形的对应角相等),
∴AC∥FE(同位角相等,两直线平行).
故答案为:两直线平行,同位角相等;AF﹣AD;∠C=∠DEF;AAS;∠BAC=∠DFE;同位角相等,两直线平行.
20.(2024秋 天门期末)有些大数值问题可以通过用字母代替数转化成整式问题来解决,请先阅读下面的解题过程,再解答下面的问题.
例:若x=6789×6786,y=6788×6787,试比较x,y的大小.
解:设6788=a,
那么x=(a+1)(a﹣2)=a2﹣a﹣2,y=a(a﹣1)=a2﹣a.
因为x﹣y=(a2﹣a﹣2)﹣(a2﹣a)=﹣2<0,即x﹣y<0,所以x<y.
看完后,你学会了这种方法吗?利用上面的方法解答下列问题:
若x=2024×2028﹣2025×2027,y=2025×2029﹣2026×2028,试比较x,y的大小.
【解答】解:设2024=a,
则x=a(a+4)﹣(a+1)(a+3)
=a2+4a﹣(a2+3a+a+3)
=a2+4a﹣a2﹣3a﹣a﹣3
=﹣3,
y=(a+1)(a+5)﹣(a+2)(a+4)
=(a2+5a+a+5)﹣(a2+4a+2a+8)
=a2+5a+a+5﹣a2﹣4a﹣2a﹣8
=﹣3,
∴x=y.
21.(2024秋 响水县期末)某商场今年国庆节期间举行有奖促销活动,凡购买一定金额的商品可参与转盘抽奖.如图,转盘分为“A”“B”“C”“D”四个区域,自由转动转盘,若指针落在字母“B”所在的区域内,则顾客中奖(转到公共线位置时重转).若某顾客转动1次转盘,求其中奖的概率.
【解答】解:由图知,字母“B”所在的区域的圆心角度数为360°﹣(60°+135°+90°)=75°,
∴当转盘停止转动后,指针落在字母“B”所在区域内的概率是,即中奖的概率是.
22.(2024秋 大理州期末)如图,某小区有一块长为(3a+2b)米,宽为(2a﹣3b)米的长方形地块,角上有四个边长为b米的小正方形空地,开发商计划将阴影部分进行绿化.
(1)求该小区绿化的总面积;
(2)若a=10,b=2,绿化成本为50元/平方米,则完成绿化共需要多少钱?
【解答】解:(1)(3a+2b)(2a﹣3b)﹣4b2
=6a2+4ab﹣9ab﹣6b2﹣4b2
=6a2﹣5ab﹣10b2,
答:该小区绿化的总面积(6a2﹣5ab﹣10b2)平方米;
(2)当a=10,b=2时,
原式=6×102﹣5×10×2﹣10×22=460,
∴50×460=23000(元).
答:完成绿化共需要23000元.
23.(2024秋 高碑店市期末)已知直线AB∥CD,E为平面内一点,点P,Q分别在直线AB,CD上,连接PE,EQ.
(1)如图1,若点E在直线AB,CD之间,求证:∠PEQ=∠BPE+∠DQE.
(2)如图2,若点E在直线AB,CD之间,PF平分∠APE,QF平分∠CQE,当∠PEQ=100°时.求∠PFQ的度数.
(3)如图3,若点E在直线AB的上方,QF平分∠CQE,PH平分∠APE,PH的反向延长线交QF于点F,当∠PEQ=50°时,求∠PFQ的度数.
【解答】(1)证明:如图1,过点E作EF∥AB,
∴∠BPE=∠PEF,
∵EF∥AB,AB∥CD,
∴EF∥CD,
∴∠DQE=∠QEF,
∵∠PEQ=∠PEF+∠QEF,
∴∠PEQ=∠BPE+∠DQE;
(2)过点F作FG∥AB,
同理(1)可得,∠PEQ=∠BPE+∠DQE=100°,
∵∠APE=180°﹣∠BPE,∠EQC=180°﹣∠DQE,
∴∠APE+∠EQC=360°﹣(∠BPE+∠DQE)=260°,
由题意可得:,,
∴,
同理(1)可得,∠PFQ=∠APF+∠CQF=130°;
(3)过点E作EG∥AB,
∴∠PEQ=∠GEQ﹣∠GEP=50°,
∵EG∥AB,
∴∠GEP=∠EPB,
∵AB∥CD,
∴GE∥CD,
∴∠GEQ=∠DQE,
∴∠DQE﹣∠EPB=50°,
由题意可得:,
∴,
∵∠CQF=∠EQF∠CQE
(180°﹣∠DQE)=90°∠DQE,
由(1)可得,
∠PFQ=∠APF+∠CQF
=90°∠EPB+90°∠DQE
=180°(∠DQE﹣∠EPB)
=180°50°
=155°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末真题检测卷-2024-2025学年数学七年级下册北师大版(2024)
一.选择题(共8小题)
1.(2024秋 滨海新区期末)考古学家们破译了玛雅人的天文历,其历法非常精确.他们计算的地球一年天数与现代相比仅差0.000069天.用科学记数法表示0.000069为( )
A.0.69×10﹣4 B.6.9×10﹣5 C.6.9×10﹣4 D.69×10﹣6
2.(2018秋 芝罘区期末)如图,一个可以自由转动的转盘被等分成6个扇形区域,并涂上了相应的颜色,转动转盘,转盘停止后,指针指向黄色区域的概率是( )
A. B. C. D.
3.(2019春 西城区期末)下列计算正确的是( )
A.a2 a3=a6 B.a8÷a2=a4
C.(a2)3=a6 D.(﹣2ab)3=﹣8a3b
4.(2024秋 禅城区期末)如图,直线m∥n,一把含30°角的直角三角尺按所示位置摆放,若∠1=30°,则∠2的度数是( )
A.20° B.25° C.30° D.40°
5.(2024秋 环江县期末)如图,线段AC的垂直平分线交AB于点D,∠A=48°,则∠BDC的度数为( )
A.48° B.96° C.90° D.84°
6.(2024秋 市北区期末)如图,能判定AB∥CD的条件是( )
A.∠1=∠3 B.∠2=∠4
C.∠DCE=∠D D.∠B+∠BAD=180°
7.(2024秋 平果市期末)如图,光线α照射到平面镜CD上,然后在平面镜AB和CD之间来回反射,光线的反射角等于入射角,若已知∠1=45°,∠3=65°,则∠2的度数为( )
A.70° B.75° C.80° D.85°
8.(2024秋 鼓楼区校级期末)已知a、b是常数,若化简(x﹣a)(2x2+bx﹣4)的结果不含x的二次项,则12a﹣6b﹣1的值为( )
A.1 B.﹣1 C.5 D.﹣13
二.填空题(共8小题)
9.(2024秋 延边州期末)已知a+b=5,ab=6.则a2+b2= .
10.(2024秋 海曙区期末)在20件样品中,有一等品10件,二等品7件,三等品3件.从中任取1件,结果为三等品的概率为 .
11.(2024秋 龙岩期末)计算:20252﹣4050×2023+20232= .
12.(2024秋 合肥期末)在△ABC中,DE,FG分别是边AB,AC的垂直平分线,分别交BC于E,G两点,连接AE,AG,若BC=8,则△AEG的周长为 .
13.(2024秋 思明区校级期末)如图,在△ABC中,AD平分∠BAC,DE⊥AB.若AC=2,DE=1,则S△ACD= .
14.(2024春 德州期末)光从一种介质射向另一种介质时会发生折射.如图,用直线m,n表示一块玻璃的两个面,且m∥n.现有一束光线AB从空气射向玻璃,BC是折射光线,D为射线AB延长线上一点.若∠1=20°,∠2=145°,则∠3= .
15.(2024秋 高新区期末)一个盒子中装有a个白球和6个红球,这些球除颜色外完全相同,若每次将球充分搅匀后,任意摸出1个球记下颜色再放回盒子,通过大量重复试验,发现摸到白球的频率稳定在60%,估计a的值为 .
16.(2024秋 高坪区期末)如图,在Rt△ABC中,∠C=90°,分别以点A、B为圆心,大于的长为半径画弧,交于点M、N,作直线MN分别交BC、AB于点D、E,连接AD.若∠B=32°,则∠CAD的度数为 °.
三.解答题(共7小题)
17.(2024秋 延边州期末)计算:(y+2)(y﹣2)﹣(y﹣1)(y﹣3).
18.(2024秋 河南期末)如图,点D在AC边上,∠A=∠B,AE=BE,∠1=∠2.
(1)求证:△AEC≌△BED;
(2)若∠1=45°,求∠BDE的度数.
19.(2024秋 呼和浩特期末)如图,在△ABC中,点D在边BA的延长线上,过点D作射线DM∥BC,点E是射线DM上一个定点.
(1)尺规作图:在射线DM上方求作∠DEF,使得∠DEF=∠C,与BA的延长线交于点F.(不用写作图步骤,保留作图痕迹)
(2)在(1)问条件下,若BD=AF,求证:AC∥FE.
请把以下的解题过程补充完整.
证明:∵DM∥BC(已知),
∴∠B=∠FDE(① ),
∵BD=AF(已知),
∴BD﹣AD=② (等式的性质),即AB=FD,
在△ABC和△FDE中,,
∴△ABC≌△FDE(④ ),
∴⑤ (全等三角形的对应角相等),
∴AC∥FE(⑥ ).
20.(2024秋 天门期末)有些大数值问题可以通过用字母代替数转化成整式问题来解决,请先阅读下面的解题过程,再解答下面的问题.
例:若x=6789×6786,y=6788×6787,试比较x,y的大小.
解:设6788=a,
那么x=(a+1)(a﹣2)=a2﹣a﹣2,y=a(a﹣1)=a2﹣a.
因为x﹣y=(a2﹣a﹣2)﹣(a2﹣a)=﹣2<0,即x﹣y<0,所以x<y.
看完后,你学会了这种方法吗?利用上面的方法解答下列问题:
若x=2024×2028﹣2025×2027,y=2025×2029﹣2026×2028,试比较x,y的大小.
21.(2024秋 响水县期末)某商场今年国庆节期间举行有奖促销活动,凡购买一定金额的商品可参与转盘抽奖.如图,转盘分为“A”“B”“C”“D”四个区域,自由转动转盘,若指针落在字母“B”所在的区域内,则顾客中奖(转到公共线位置时重转).若某顾客转动1次转盘,求其中奖的概率.
22.(2024秋 大理州期末)如图,某小区有一块长为(3a+2b)米,宽为(2a﹣3b)米的长方形地块,角上有四个边长为b米的小正方形空地,开发商计划将阴影部分进行绿化.
(1)求该小区绿化的总面积;
(2)若a=10,b=2,绿化成本为50元/平方米,则完成绿化共需要多少钱?
23.(2024秋 高碑店市期末)已知直线AB∥CD,E为平面内一点,点P,Q分别在直线AB,CD上,连接PE,EQ.
(1)如图1,若点E在直线AB,CD之间,求证:∠PEQ=∠BPE+∠DQE.
(2)如图2,若点E在直线AB,CD之间,PF平分∠APE,QF平分∠CQE,当∠PEQ=100°时.求∠PFQ的度数.
(3)如图3,若点E在直线AB的上方,QF平分∠CQE,PH平分∠APE,PH的反向延长线交QF于点F,当∠PEQ=50°时,求∠PFQ的度数.
期末真题检测卷-2024-2025学年数学七年级下册北师大版(2024)
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 B A C C B B D B.
一.选择题(共8小题)
1.(2024秋 滨海新区期末)考古学家们破译了玛雅人的天文历,其历法非常精确.他们计算的地球一年天数与现代相比仅差0.000069天.用科学记数法表示0.000069为( )
A.0.69×10﹣4 B.6.9×10﹣5 C.6.9×10﹣4 D.69×10﹣6
【解答】解:0.000069=6.9×10﹣5;
故选:B.
2.(2018秋 芝罘区期末)如图,一个可以自由转动的转盘被等分成6个扇形区域,并涂上了相应的颜色,转动转盘,转盘停止后,指针指向黄色区域的概率是( )
A. B. C. D.
【解答】解:∵转盘被等分成6个扇形区域,
而黄色区域占其中的一个,
∴指针指向黄色区域的概率.
故选:A.
3.(2019春 西城区期末)下列计算正确的是( )
A.a2 a3=a6 B.a8÷a2=a4
C.(a2)3=a6 D.(﹣2ab)3=﹣8a3b
【解答】解:A、a2 a3=a5,故此选项错误;
B、a8÷a2=a6,故此选项错误;
C、(a2)3=a6,正确;
D、(﹣2ab)3=﹣8a3b3,故此选项错误;
故选:C.
4.(2024秋 禅城区期末)如图,直线m∥n,一把含30°角的直角三角尺按所示位置摆放,若∠1=30°,则∠2的度数是( )
A.20° B.25° C.30° D.40°
【解答】解:如图:
∵∠1=30°,∠4=90°,
∴∠DCB=∠1+∠4=120°,
∵直线m∥n,
∴∠ABC=180°﹣∠BCD=60°,
∵∠3=30°,
∴∠2=∠ABC﹣∠3=30°,
故选:C.
5.(2024秋 环江县期末)如图,线段AC的垂直平分线交AB于点D,∠A=48°,则∠BDC的度数为( )
A.48° B.96° C.90° D.84°
【解答】解:∵DE是线段AC的垂直平分线,
∴DA=DC,
∴∠DCA=∠A=48°,
∴∠BDC=∠DCA+∠A=96°,
故选:B.
6.(2024秋 市北区期末)如图,能判定AB∥CD的条件是( )
A.∠1=∠3 B.∠2=∠4
C.∠DCE=∠D D.∠B+∠BAD=180°
【解答】解:A.当∠1=∠3时,不能得到AB∥CD,故A选项错误;
B.当∠2=∠4时,能得到AB∥CD,故B选项正确;
C.当∠DCE=∠D时,不能得到AB∥CD,故C选项错误;
D.当∠B+∠BAD=180°时,不能得到AB∥CD,故D选项错误;
故选:B.
7.(2024秋 平果市期末)如图,光线α照射到平面镜CD上,然后在平面镜AB和CD之间来回反射,光线的反射角等于入射角,若已知∠1=45°,∠3=65°,则∠2的度数为( )
A.70° B.75° C.80° D.85°
【解答】解:根据题意可得,∠4=∠1=45°,∠5=∠3=65°,∠2=∠6,
由三角形内角和定理和平角的定义得∠2=180°﹣45°﹣(180°﹣65°×2)=85°;
故选:D.
8.(2024秋 鼓楼区校级期末)已知a、b是常数,若化简(x﹣a)(2x2+bx﹣4)的结果不含x的二次项,则12a﹣6b﹣1的值为( )
A.1 B.﹣1 C.5 D.﹣13
【解答】解:∵多项式(x﹣a)(2x2+bx﹣4)=2x3+(﹣2a+b)x2+(﹣ab﹣4)x+4a不含x的二次项,
∴﹣2a+b=0,
解得b=2a,
∴12a﹣6b﹣1=12a﹣6×2a﹣1=﹣1.
故选:B.
二.填空题(共8小题)
9.(2024秋 延边州期末)已知a+b=5,ab=6.则a2+b2= 13 .
【解答】解:∵a+b=5,
∴(a+b)2=25,
∴a2+2ab+b2=25.
∵ab=6,
∴a2+b2+12=25,
∴a2+b2=13.
故答案为:13.
10.(2024秋 海曙区期末)在20件样品中,有一等品10件,二等品7件,三等品3件.从中任取1件,结果为三等品的概率为 .
【解答】解:∵共20件样品,三等品有3件,
∴从中任取1件,结果为三等品的概率为,
故答案为:.
11.(2024秋 龙岩期末)计算:20252﹣4050×2023+20232= 4 .
【解答】解:原式=20252﹣2×2025×2023+20232
=(2025﹣2023)2
=22
=4.
故答案为:4.
12.(2024秋 合肥期末)在△ABC中,DE,FG分别是边AB,AC的垂直平分线,分别交BC于E,G两点,连接AE,AG,若BC=8,则△AEG的周长为 8 .
【解答】解:∵DE,FG分别是边AB,AC的垂直平分线,
∴AE=BE,AG=CG,
∴BC=BE+EG+CG=AE+EG+AG,
∴△AEG的周长=AE+EG+AG=BC=8.
故答案为:8.
13.(2024秋 思明区校级期末)如图,在△ABC中,AD平分∠BAC,DE⊥AB.若AC=2,DE=1,则S△ACD= 1 .
【解答】解:过点D作DF⊥AC,垂足为F,
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF=1,
∵AC=2,
∴S△ACDAC DF
2×1
=1,
故答案为:1.
14.(2024春 德州期末)光从一种介质射向另一种介质时会发生折射.如图,用直线m,n表示一块玻璃的两个面,且m∥n.现有一束光线AB从空气射向玻璃,BC是折射光线,D为射线AB延长线上一点.若∠1=20°,∠2=145°,则∠3= 125° .
【解答】解:∵∠2=145°,∠1=20°,
∴∠DBE=180°﹣145°=35°,
∴∠CBE=∠1+∠DBE=20°+35°=55°,
∵m∥n,
∴∠3=180°﹣55°=125°.
故答案为:125°.
15.(2024秋 高新区期末)一个盒子中装有a个白球和6个红球,这些球除颜色外完全相同,若每次将球充分搅匀后,任意摸出1个球记下颜色再放回盒子,通过大量重复试验,发现摸到白球的频率稳定在60%,估计a的值为 9 .
【解答】解:由题意可得,60%,
解得,a=9.
经检验,a=9是分式方程的解且符合题意,
故答案为:9.
16.(2024秋 高坪区期末)如图,在Rt△ABC中,∠C=90°,分别以点A、B为圆心,大于的长为半径画弧,交于点M、N,作直线MN分别交BC、AB于点D、E,连接AD.若∠B=32°,则∠CAD的度数为 26 °.
【解答】解:由作法得MN垂直平分AB,
∴AD=BD,
∴∠DAB=∠B=32°,
∵∠C=90°,
∴∠BAC=90°﹣∠B=90°﹣32°=58°,
∴∠CAD=∠BAC﹣∠BAD=58°﹣32°=26°.
故答案为:26.
三.解答题(共7小题)
17.(2024秋 延边州期末)计算:(y+2)(y﹣2)﹣(y﹣1)(y﹣3).
【解答】解:(y+2)(y﹣2)﹣(y﹣1)(y﹣3)
=y2﹣4﹣(y2﹣3y﹣y+3)
=y2﹣4﹣y2+3y+y﹣3
=4y﹣7.
18.(2024秋 河南期末)如图,点D在AC边上,∠A=∠B,AE=BE,∠1=∠2.
(1)求证:△AEC≌△BED;
(2)若∠1=45°,求∠BDE的度数.
【解答】(1)证明:∵∠1=∠2,∠2+∠BDE=∠ADE=∠1+∠C,
∴∠BDE=∠C,
在△AEC和△BED中,
,
∴△AEC≌△BED(AAS),
(2)解:∵△AEC≌△BED,
∴ED=EC,
∴∠C=∠EDC,
∵∠1=45°,
∴,
∴∠BDE=67.5°.
19.(2024秋 呼和浩特期末)如图,在△ABC中,点D在边BA的延长线上,过点D作射线DM∥BC,点E是射线DM上一个定点.
(1)尺规作图:在射线DM上方求作∠DEF,使得∠DEF=∠C,与BA的延长线交于点F.(不用写作图步骤,保留作图痕迹)
(2)在(1)问条件下,若BD=AF,求证:AC∥FE.
请把以下的解题过程补充完整.
证明:∵DM∥BC(已知),
∴∠B=∠FDE(① 两直线平行,同位角相等 ),
∵BD=AF(已知),
∴BD﹣AD=② AF﹣AD (等式的性质),即AB=FD,
在△ABC和△FDE中,,
∴△ABC≌△FDE(④ AAS ),
∴⑤ ∠BAC=∠DFE (全等三角形的对应角相等),
∴AC∥FE(⑥ 同位角相等,两直线平行 ).
【解答】(1)解:如图,∠DEF即为所求;
(2)证明:∵DM∥BC(已知),
∴∠B=∠FDE(两直线平行,同位角相等),
∵BD=AF(已知),
∴BD﹣AD=AF﹣AD(等式的性质),
∴AB=FD
在△ABC和△FDE中,
.
∴△ABC≌△FDE(AAS),
∴∠BAC=∠DFE(全等三角形的对应角相等),
∴AC∥FE(同位角相等,两直线平行).
故答案为:两直线平行,同位角相等;AF﹣AD;∠C=∠DEF;AAS;∠BAC=∠DFE;同位角相等,两直线平行.
20.(2024秋 天门期末)有些大数值问题可以通过用字母代替数转化成整式问题来解决,请先阅读下面的解题过程,再解答下面的问题.
例:若x=6789×6786,y=6788×6787,试比较x,y的大小.
解:设6788=a,
那么x=(a+1)(a﹣2)=a2﹣a﹣2,y=a(a﹣1)=a2﹣a.
因为x﹣y=(a2﹣a﹣2)﹣(a2﹣a)=﹣2<0,即x﹣y<0,所以x<y.
看完后,你学会了这种方法吗?利用上面的方法解答下列问题:
若x=2024×2028﹣2025×2027,y=2025×2029﹣2026×2028,试比较x,y的大小.
【解答】解:设2024=a,
则x=a(a+4)﹣(a+1)(a+3)
=a2+4a﹣(a2+3a+a+3)
=a2+4a﹣a2﹣3a﹣a﹣3
=﹣3,
y=(a+1)(a+5)﹣(a+2)(a+4)
=(a2+5a+a+5)﹣(a2+4a+2a+8)
=a2+5a+a+5﹣a2﹣4a﹣2a﹣8
=﹣3,
∴x=y.
21.(2024秋 响水县期末)某商场今年国庆节期间举行有奖促销活动,凡购买一定金额的商品可参与转盘抽奖.如图,转盘分为“A”“B”“C”“D”四个区域,自由转动转盘,若指针落在字母“B”所在的区域内,则顾客中奖(转到公共线位置时重转).若某顾客转动1次转盘,求其中奖的概率.
【解答】解:由图知,字母“B”所在的区域的圆心角度数为360°﹣(60°+135°+90°)=75°,
∴当转盘停止转动后,指针落在字母“B”所在区域内的概率是,即中奖的概率是.
22.(2024秋 大理州期末)如图,某小区有一块长为(3a+2b)米,宽为(2a﹣3b)米的长方形地块,角上有四个边长为b米的小正方形空地,开发商计划将阴影部分进行绿化.
(1)求该小区绿化的总面积;
(2)若a=10,b=2,绿化成本为50元/平方米,则完成绿化共需要多少钱?
【解答】解:(1)(3a+2b)(2a﹣3b)﹣4b2
=6a2+4ab﹣9ab﹣6b2﹣4b2
=6a2﹣5ab﹣10b2,
答:该小区绿化的总面积(6a2﹣5ab﹣10b2)平方米;
(2)当a=10,b=2时,
原式=6×102﹣5×10×2﹣10×22=460,
∴50×460=23000(元).
答:完成绿化共需要23000元.
23.(2024秋 高碑店市期末)已知直线AB∥CD,E为平面内一点,点P,Q分别在直线AB,CD上,连接PE,EQ.
(1)如图1,若点E在直线AB,CD之间,求证:∠PEQ=∠BPE+∠DQE.
(2)如图2,若点E在直线AB,CD之间,PF平分∠APE,QF平分∠CQE,当∠PEQ=100°时.求∠PFQ的度数.
(3)如图3,若点E在直线AB的上方,QF平分∠CQE,PH平分∠APE,PH的反向延长线交QF于点F,当∠PEQ=50°时,求∠PFQ的度数.
【解答】(1)证明:如图1,过点E作EF∥AB,
∴∠BPE=∠PEF,
∵EF∥AB,AB∥CD,
∴EF∥CD,
∴∠DQE=∠QEF,
∵∠PEQ=∠PEF+∠QEF,
∴∠PEQ=∠BPE+∠DQE;
(2)过点F作FG∥AB,
同理(1)可得,∠PEQ=∠BPE+∠DQE=100°,
∵∠APE=180°﹣∠BPE,∠EQC=180°﹣∠DQE,
∴∠APE+∠EQC=360°﹣(∠BPE+∠DQE)=260°,
由题意可得:,,
∴,
同理(1)可得,∠PFQ=∠APF+∠CQF=130°;
(3)过点E作EG∥AB,
∴∠PEQ=∠GEQ﹣∠GEP=50°,
∵EG∥AB,
∴∠GEP=∠EPB,
∵AB∥CD,
∴GE∥CD,
∴∠GEQ=∠DQE,
∴∠DQE﹣∠EPB=50°,
由题意可得:,
∴,
∵∠CQF=∠EQF∠CQE
(180°﹣∠DQE)=90°∠DQE,
由(1)可得,
∠PFQ=∠APF+∠CQF
=90°∠EPB+90°∠DQE
=180°(∠DQE﹣∠EPB)
=180°50°
=155°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
