华师大七年级下册第8章8.1认识不等式
文档属性
| 名称 | 华师大七年级下册第8章8.1认识不等式 |  | |
| 格式 | doc | ||
| 文件大小 | 382.5KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-21 17:01:19 | ||
图片预览

文档简介
登陆21世纪教育 助您教考全无忧
华师大版七年级下册第8章第1节8.1认识不等式课时练习
一、单选题(共15小题)
1.下列按条件列出的不等式中,正确的是 ( )
A.a不是负数,则a>0 B.a与3的差不等于1,则a﹣3<1
C.a是不小于0的数,则a>0 D.a与b的和是非负数,则a+b≥0
答案:D
解答:A选项a不是负数表达为,故A错误;B选项a与3的差不等于1,表达为,故B错误;C选项a是不小于0的数表达为,故C错误;唯有D选项表达正确,故选D.
分析:不等式有以下五个符号表达“>、<、、、”,注意区分选项中的描述包括哪些部分,选择正确的表达形式.
2.根据数量关系“x为非负数”所列出的不等式是( )
A.x>0 B.x<0 C.x≥0 D.x≤0
答案:C
解答:根据题目陈述x为非负数,即包含大于和等于0两种情况,用“”符号表达,故不等式的形式是“x≥0”,故选C.
分析:根据题目陈述,选择正确的不等式形式,应包含题目陈述的所有情况.
3.下面列出的不等式中,正确的是( )
A.a不是负数,可表示成a>0
B.x不大于3,可表示成x<3
C.m与4的差是负数,可表示成m﹣4<0
D.x与2的和是非负数,可表示成x+2>0
答案:C
解答:A选项的表达式为,B选项的表达式为,C选项的表达式正确,D选项的表达式为,故选C.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )分析:熟悉不等式表达式的五种基本形式,根据题目陈述所包含的数量关系选择正确的不等号.
4.下面的式子中,不属于不等式的是( ).
A. B. C. D.
答案:B
解答:不等式由五类基本不等号连接“>、<、、、”,没有这些不等号连接的都不是不等式,B选项是个等号连接的代数式,所以B不是不等式,故选B.
分析:理解不等关系的建立,以及基本的不等号形式,明确什么是不等式.
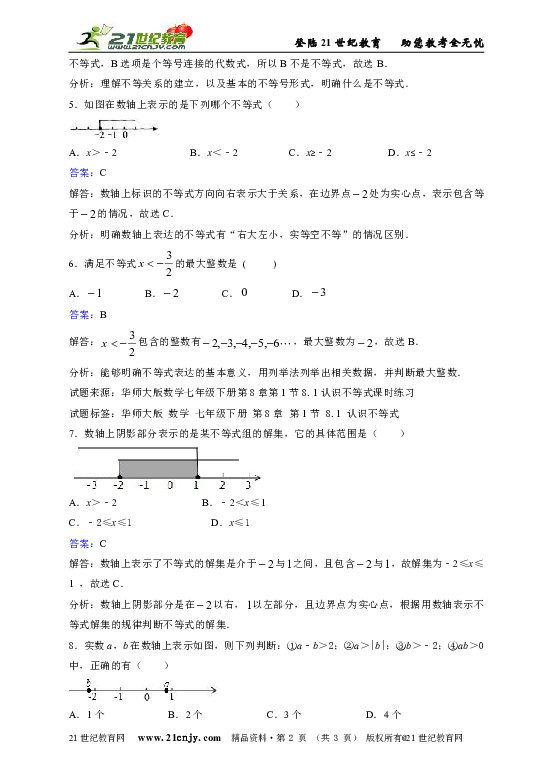
5.如图在数轴上表示的是下列哪个不等式( )
A.x>﹣2 B.x<﹣2 C.x≥﹣2 D.x≤﹣2
答案:C
解答:数轴上标识的不等式方向向右表示大于关系,在边界点处为实心点,表示包含等于的情况,故选C.
分析:明确数轴上表达的不等式有“右大左小,实等空不等”的情况区别.
6.满足不等式的最大整数是 ( )
A. B. C. D.
答案:B
解答:包含的整数有,最大整数为,故选B.
分析:能够明确不等式表达的基本意义,用列举法列举出相关数据,并判断最大整数.
试题来源:华师大版数学七年级下册第8章第1节8.1认识不等式课时练习
试题标签:华师大版 数学 七年级下册 第8章 第1节 8.1 认识不等式
7.数轴上阴影部分表示的是某不等式组的解集,它的具体范围是( )
A.x>﹣2 B.﹣2<x≤1
C.﹣2≤x≤1 D.x≤1
答案:C
解答:数轴上表示了不等式的解集是介于与之间,且包含与,故解集为﹣2≤x≤1 ,故选C.
分析:数轴上阴影部分是在以右,以左部分,且边界点为实心点,根据用数轴表示不等式解集的规律判断不等式的解集.
8.实数a,b在数轴上表示如图,则下列判断:①a﹣b>2;②a>|b|;③b>﹣2;④ab>0中,正确的有( )
A.1个 B.2个 C.3个 D.4个
答案:A
解答:在数轴上在右边两个单位以外,故①a﹣b>2正确;因为,,所以,所以②)a>|b|不正确,③b>﹣2不正确;④ab>0不正确,故只有一个判断正确,故选A.
分析:能够根据数轴上表示点的位置确定点代表的数的大小关系,和与特殊值的大小比较.
9.据丽水气象台"天气预报"报道,今天的最低气温是 17 C ,最高气温是 25 C ,则今天气温 t( C) 的范围是 ( )
A.t<17 B.t>25 C.t=21 D.17≤t≤25
答案:D
解答:今天的气温范围是介于最低气温与最高气温之间的范围,故表达为17≤t≤25,故选D.
分析:能够根据题目陈述,判断不等式的解集范围,是学生学习不等式知识的一个基础知识.
10.下列不等式的解集中,不包括-4 的是 ( )
A.x≤-4 B.x≥-4 C.x≤-5 D.x≥-5
答案:C
解答:选项A与选项B中是边界点,且不等式包含等于边界点的情况,C中由于,故不包含,D中由于,故包含,故选C.
分析:能够根据题目陈述把握某特定值是否在不等式的解集当中,可用比较法或数轴表示法两种方法进行判断.
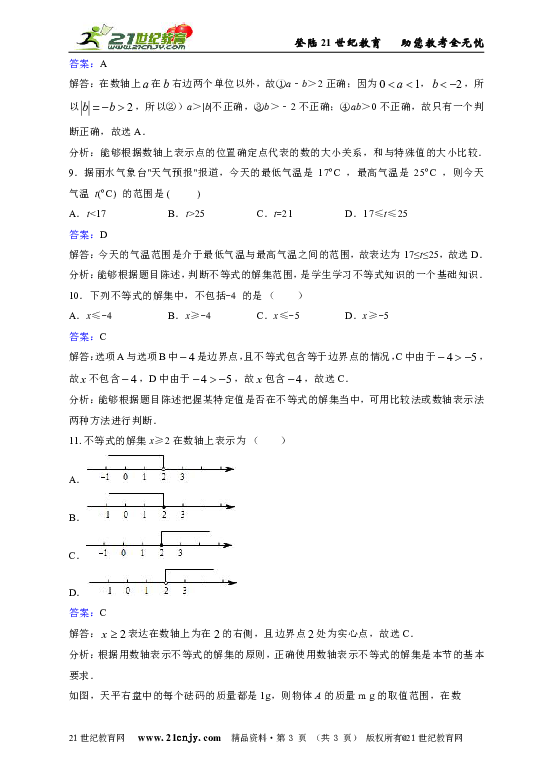
11.不等式的解集x≥2在数轴上表示为 ( )
A.
B.
C.
D.
答案:C
解答:表达在数轴上为在的右侧,且边界点处为实心点,故选C.
分析:根据用数轴表示不等式的解集的原则,正确使用数轴表示不等式的解集是本节的基本要求.
12.如图,天平右盘中的每个砝码的质量都是1g,则物体A的质量m g的取值范围,在数轴上表示为 ( )
A.
B.
C.
D.
答案:A
解答:根据天平的测量,可知物体的质量的不等式表达为,用数轴表示为A,故选A.
分析:根据天平的测量,先判断的不等式表达形式,然后选择正确的数轴表示形式.
13.王芳同学到文具店购买中性笔和笔记本,中性笔每支0.8元,笔记本每本1.2元,王芳同学花了10元钱,则可供她选择的购买方案的个数为(两样都买,余下的钱少于0.8 元) ( )
A.6 B.7 C.8 D.9
答案:B
解答:设王芳同学购买中性笔个,笔记本个,由题意得,化简得,因为、均为正整数,所以为正整数,所以有或,当时,,则为偶数且为3的倍数,故有三种方案(分别为;;);当时,,则为奇数且为3的倍数,故四种方案(分别为;;;;),共故有七种方案,故选B.
分析:理解题目陈述,明确不等式范围,并建立不等式,由隐含条件、均为正整数,先求解代数式的值,进而判断方案个数.
14.在数学表达式①-3<0;②4x+5>0; ③x=3; ④x2+x; ⑤ x -4; ⑥ x+2>x+1是不等式的有 ( )
A.2个 B.3个 C.4个 D.5个
答案:C
解答:由不等式的性质,知①、②、⑤、⑥四项是不等式,故选C.
15.分析:充分理解不等式的性质,明确由不等号连接的式子是不等式.
16.下列由题意列出的不等关系中, 错误的是( )
A.a不是负数可表示为a>0
B. x不大于3可表示为
C.m与4的差是非负数,可表示为x-4≥0
D.代数式 x2+3必大于3x-7,可表示为x2+3>3x-7
答案:A
解答:选项A“a不是负数”应表示为,故选A.
分析:理解不是负数可能是正数或0,不等式应包括这两种情况.
二、填空题(共5小题)
16.选择适当的不等号填空:
(1)﹣1 0;
答案:<
(2) 7;
答案:<
(3) 0;
答案:
(4)|a| a.
答案:
解答:(1)由负数小于0;(2)
(3)由二次方根知,当时,=0,当时<0.
(4)当时,|a|a;当时,|a|>a
分析:含有根号的式子都放在根式内比较大小;含有字母的式子注意取值范围和分情况讨论.
17. 根据题意列出不等式:y的一半与3的差是负数 .
答案:
解答:“y的一半与3的差”表示为,负数即小于0,故表达式为.
分析:根据题目陈述,列出代数式,正负数即与0的大小比较,通过此关系列出不等式.
18.满足﹣1.2<x≤3的整数有 个.
答案: 5
解答:由题意,满足不等式﹣1.2<x≤3的整数有,共5个.
分析:根据题意,求出满足条件的整数解是学习了不等式的性质以后应该熟练掌握的基本能力.
19. 选择适当的不等号填空:
(1)2 ﹣3;
答案:>
(2) .
答案:>
解答:(1)正数大于负数 (2)负数的绝对值越小其数值越大 .
分析:学会正数与负数的大小比较规律,负数与负数的大小比较规律.
20.用适当的不等号填空:
(1) 0;
答案:<
(2)﹣1.8 ;
答案:>
(3)6×4 6×(﹣4);
答案:>
(4)若分式有意义,则x 1;
答案:
(5)y2﹣4y+4 0.
答案:
解答:(1)负数小于0;(2)负数的绝对值越小其数值越大;(3)正数大于负数;(4)分式的分母不等于0;(5).
分析:熟练掌握正数大于0,负数小于0,正数大于负数,负数的绝对值越小其数值越大,分式的分母不等于0,完全平方式大于等于0.
三、解答题(共5小题)
21.根据下列数量关系,列出不等式:
(1)x的3倍大于x;
答案:
解答:的3倍即,用大于号连接,所以x的3倍大于x即.
(2)m与1的相反数的和不小于;
答案:
解答:1的相反数即为,与1的相反数的和为,不小于即用大于等于符号连接,故不等式为.
(3)a与﹣2的差不大于它的3倍;
答案:
解答:与的差即为,它的3倍即为,中间用不大于即小于等于符号连接即为.
(4)a,b两数的平方和不小于它们的积的2倍.
答案:
解答:a,b两数的平方和即为,它们的积的2倍即为,中间用不小于即大于等于符号连接表示为.
分析:注意题目当中包含不大于、不小于等字句时如何用相应的不等号表达.
22.比较下面每小题中两个算式结果的大小(在横线上填“>”、“<”或“=”).
(1) 32+42 2×3×4;
答案:>
解答:因为,,所以
(2)22+22 2×2×2;
答案:=
解答:因为,,所以
(3)12+ 2×1×;
答案:>
解答:因为,,所以
(4)(﹣2)2+52 2×(﹣2)×5;
答案:>
解答:因为,,所以
(5) .
答案:>
解答:因为,,所以
通过观察上面的算式,请你用字母来表示上面算式中反映的一般规律.
答案:(当且仅当时,等号成立)
解答:由上述特例,发现当时,,当时,,故可总结出一般规律为(当且仅当时,等号成立)
分析:根据题目所列举特例,分析数字特征与不等号的方向提炼并总结出一般规律,规律应能体现通用性.
23.某校规定期中考试成绩的40%和期末考试成绩的60%的和作为学生成绩总成绩.该校骆红同学期中数学靠了85分,她希望自己学期总成绩不低于90分,她在期末考试中数学至少应得多少分
答案:94
解答:设她在期末考试中数学考试成绩为,由题意得
,解之得,所以最低取
分析:通过题目陈述列出不等式,并计算不等式的解集,是学习不等式的基础.
24. 某次数学测验,共有16道选择题,评分方法是:答对一题得6分,不答或答错一题扣2分,某同学要想得分为60分以上,他至少应答对多少道题?(只列关系式).
答案:.
解答:设他答对道题,则不答或答错道题,由题意得:
分析:根据题目陈述加分减分规则列出不等式,读懂题意,并用数学表达式正确表达文字陈述是逻辑性的基本体现.
25. 小明存款600元,小李存款1800元,从本月起,小明每月存款400元,小李每月存款100元,试问经过几过月,小明的存款会超过小李?
答案:5
解答:设经过个月后,小明的存款会超过小李,由题意得:
,解之得,取最小正整数为
答:经过5个月后,小明的存款会超过小李.
分析:根据题目陈述列出不等式,并正确求解,是把文字陈述转化成数学语言的一种基本能力的体现,从而实现了数学的方法解答实际问题,充分体现了学以致用的观点.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 9 页 (共 9 页) 版权所有@21世纪教育网
华师大版七年级下册第8章第1节8.1认识不等式课时练习
一、单选题(共15小题)
1.下列按条件列出的不等式中,正确的是 ( )
A.a不是负数,则a>0 B.a与3的差不等于1,则a﹣3<1
C.a是不小于0的数,则a>0 D.a与b的和是非负数,则a+b≥0
答案:D
解答:A选项a不是负数表达为,故A错误;B选项a与3的差不等于1,表达为,故B错误;C选项a是不小于0的数表达为,故C错误;唯有D选项表达正确,故选D.
分析:不等式有以下五个符号表达“>、<、、、”,注意区分选项中的描述包括哪些部分,选择正确的表达形式.
2.根据数量关系“x为非负数”所列出的不等式是( )
A.x>0 B.x<0 C.x≥0 D.x≤0
答案:C
解答:根据题目陈述x为非负数,即包含大于和等于0两种情况,用“”符号表达,故不等式的形式是“x≥0”,故选C.
分析:根据题目陈述,选择正确的不等式形式,应包含题目陈述的所有情况.
3.下面列出的不等式中,正确的是( )
A.a不是负数,可表示成a>0
B.x不大于3,可表示成x<3
C.m与4的差是负数,可表示成m﹣4<0
D.x与2的和是非负数,可表示成x+2>0
答案:C
解答:A选项的表达式为,B选项的表达式为,C选项的表达式正确,D选项的表达式为,故选C.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )分析:熟悉不等式表达式的五种基本形式,根据题目陈述所包含的数量关系选择正确的不等号.
4.下面的式子中,不属于不等式的是( ).
A. B. C. D.
答案:B
解答:不等式由五类基本不等号连接“>、<、、、”,没有这些不等号连接的都不是不等式,B选项是个等号连接的代数式,所以B不是不等式,故选B.
分析:理解不等关系的建立,以及基本的不等号形式,明确什么是不等式.
5.如图在数轴上表示的是下列哪个不等式( )
A.x>﹣2 B.x<﹣2 C.x≥﹣2 D.x≤﹣2
答案:C
解答:数轴上标识的不等式方向向右表示大于关系,在边界点处为实心点,表示包含等于的情况,故选C.
分析:明确数轴上表达的不等式有“右大左小,实等空不等”的情况区别.
6.满足不等式的最大整数是 ( )
A. B. C. D.
答案:B
解答:包含的整数有,最大整数为,故选B.
分析:能够明确不等式表达的基本意义,用列举法列举出相关数据,并判断最大整数.
试题来源:华师大版数学七年级下册第8章第1节8.1认识不等式课时练习
试题标签:华师大版 数学 七年级下册 第8章 第1节 8.1 认识不等式
7.数轴上阴影部分表示的是某不等式组的解集,它的具体范围是( )
A.x>﹣2 B.﹣2<x≤1
C.﹣2≤x≤1 D.x≤1
答案:C
解答:数轴上表示了不等式的解集是介于与之间,且包含与,故解集为﹣2≤x≤1 ,故选C.
分析:数轴上阴影部分是在以右,以左部分,且边界点为实心点,根据用数轴表示不等式解集的规律判断不等式的解集.
8.实数a,b在数轴上表示如图,则下列判断:①a﹣b>2;②a>|b|;③b>﹣2;④ab>0中,正确的有( )
A.1个 B.2个 C.3个 D.4个
答案:A
解答:在数轴上在右边两个单位以外,故①a﹣b>2正确;因为,,所以,所以②)a>|b|不正确,③b>﹣2不正确;④ab>0不正确,故只有一个判断正确,故选A.
分析:能够根据数轴上表示点的位置确定点代表的数的大小关系,和与特殊值的大小比较.
9.据丽水气象台"天气预报"报道,今天的最低气温是 17 C ,最高气温是 25 C ,则今天气温 t( C) 的范围是 ( )
A.t<17 B.t>25 C.t=21 D.17≤t≤25
答案:D
解答:今天的气温范围是介于最低气温与最高气温之间的范围,故表达为17≤t≤25,故选D.
分析:能够根据题目陈述,判断不等式的解集范围,是学生学习不等式知识的一个基础知识.
10.下列不等式的解集中,不包括-4 的是 ( )
A.x≤-4 B.x≥-4 C.x≤-5 D.x≥-5
答案:C
解答:选项A与选项B中是边界点,且不等式包含等于边界点的情况,C中由于,故不包含,D中由于,故包含,故选C.
分析:能够根据题目陈述把握某特定值是否在不等式的解集当中,可用比较法或数轴表示法两种方法进行判断.
11.不等式的解集x≥2在数轴上表示为 ( )
A.
B.
C.
D.
答案:C
解答:表达在数轴上为在的右侧,且边界点处为实心点,故选C.
分析:根据用数轴表示不等式的解集的原则,正确使用数轴表示不等式的解集是本节的基本要求.
12.如图,天平右盘中的每个砝码的质量都是1g,则物体A的质量m g的取值范围,在数轴上表示为 ( )
A.
B.
C.
D.
答案:A
解答:根据天平的测量,可知物体的质量的不等式表达为,用数轴表示为A,故选A.
分析:根据天平的测量,先判断的不等式表达形式,然后选择正确的数轴表示形式.
13.王芳同学到文具店购买中性笔和笔记本,中性笔每支0.8元,笔记本每本1.2元,王芳同学花了10元钱,则可供她选择的购买方案的个数为(两样都买,余下的钱少于0.8 元) ( )
A.6 B.7 C.8 D.9
答案:B
解答:设王芳同学购买中性笔个,笔记本个,由题意得,化简得,因为、均为正整数,所以为正整数,所以有或,当时,,则为偶数且为3的倍数,故有三种方案(分别为;;);当时,,则为奇数且为3的倍数,故四种方案(分别为;;;;),共故有七种方案,故选B.
分析:理解题目陈述,明确不等式范围,并建立不等式,由隐含条件、均为正整数,先求解代数式的值,进而判断方案个数.
14.在数学表达式①-3<0;②4x+5>0; ③x=3; ④x2+x; ⑤ x -4; ⑥ x+2>x+1是不等式的有 ( )
A.2个 B.3个 C.4个 D.5个
答案:C
解答:由不等式的性质,知①、②、⑤、⑥四项是不等式,故选C.
15.分析:充分理解不等式的性质,明确由不等号连接的式子是不等式.
16.下列由题意列出的不等关系中, 错误的是( )
A.a不是负数可表示为a>0
B. x不大于3可表示为
C.m与4的差是非负数,可表示为x-4≥0
D.代数式 x2+3必大于3x-7,可表示为x2+3>3x-7
答案:A
解答:选项A“a不是负数”应表示为,故选A.
分析:理解不是负数可能是正数或0,不等式应包括这两种情况.
二、填空题(共5小题)
16.选择适当的不等号填空:
(1)﹣1 0;
答案:<
(2) 7;
答案:<
(3) 0;
答案:
(4)|a| a.
答案:
解答:(1)由负数小于0;(2)
(3)由二次方根知,当时,=0,当时<0.
(4)当时,|a|a;当时,|a|>a
分析:含有根号的式子都放在根式内比较大小;含有字母的式子注意取值范围和分情况讨论.
17. 根据题意列出不等式:y的一半与3的差是负数 .
答案:
解答:“y的一半与3的差”表示为,负数即小于0,故表达式为.
分析:根据题目陈述,列出代数式,正负数即与0的大小比较,通过此关系列出不等式.
18.满足﹣1.2<x≤3的整数有 个.
答案: 5
解答:由题意,满足不等式﹣1.2<x≤3的整数有,共5个.
分析:根据题意,求出满足条件的整数解是学习了不等式的性质以后应该熟练掌握的基本能力.
19. 选择适当的不等号填空:
(1)2 ﹣3;
答案:>
(2) .
答案:>
解答:(1)正数大于负数 (2)负数的绝对值越小其数值越大 .
分析:学会正数与负数的大小比较规律,负数与负数的大小比较规律.
20.用适当的不等号填空:
(1) 0;
答案:<
(2)﹣1.8 ;
答案:>
(3)6×4 6×(﹣4);
答案:>
(4)若分式有意义,则x 1;
答案:
(5)y2﹣4y+4 0.
答案:
解答:(1)负数小于0;(2)负数的绝对值越小其数值越大;(3)正数大于负数;(4)分式的分母不等于0;(5).
分析:熟练掌握正数大于0,负数小于0,正数大于负数,负数的绝对值越小其数值越大,分式的分母不等于0,完全平方式大于等于0.
三、解答题(共5小题)
21.根据下列数量关系,列出不等式:
(1)x的3倍大于x;
答案:
解答:的3倍即,用大于号连接,所以x的3倍大于x即.
(2)m与1的相反数的和不小于;
答案:
解答:1的相反数即为,与1的相反数的和为,不小于即用大于等于符号连接,故不等式为.
(3)a与﹣2的差不大于它的3倍;
答案:
解答:与的差即为,它的3倍即为,中间用不大于即小于等于符号连接即为.
(4)a,b两数的平方和不小于它们的积的2倍.
答案:
解答:a,b两数的平方和即为,它们的积的2倍即为,中间用不小于即大于等于符号连接表示为.
分析:注意题目当中包含不大于、不小于等字句时如何用相应的不等号表达.
22.比较下面每小题中两个算式结果的大小(在横线上填“>”、“<”或“=”).
(1) 32+42 2×3×4;
答案:>
解答:因为,,所以
(2)22+22 2×2×2;
答案:=
解答:因为,,所以
(3)12+ 2×1×;
答案:>
解答:因为,,所以
(4)(﹣2)2+52 2×(﹣2)×5;
答案:>
解答:因为,,所以
(5) .
答案:>
解答:因为,,所以
通过观察上面的算式,请你用字母来表示上面算式中反映的一般规律.
答案:(当且仅当时,等号成立)
解答:由上述特例,发现当时,,当时,,故可总结出一般规律为(当且仅当时,等号成立)
分析:根据题目所列举特例,分析数字特征与不等号的方向提炼并总结出一般规律,规律应能体现通用性.
23.某校规定期中考试成绩的40%和期末考试成绩的60%的和作为学生成绩总成绩.该校骆红同学期中数学靠了85分,她希望自己学期总成绩不低于90分,她在期末考试中数学至少应得多少分
答案:94
解答:设她在期末考试中数学考试成绩为,由题意得
,解之得,所以最低取
分析:通过题目陈述列出不等式,并计算不等式的解集,是学习不等式的基础.
24. 某次数学测验,共有16道选择题,评分方法是:答对一题得6分,不答或答错一题扣2分,某同学要想得分为60分以上,他至少应答对多少道题?(只列关系式).
答案:.
解答:设他答对道题,则不答或答错道题,由题意得:
分析:根据题目陈述加分减分规则列出不等式,读懂题意,并用数学表达式正确表达文字陈述是逻辑性的基本体现.
25. 小明存款600元,小李存款1800元,从本月起,小明每月存款400元,小李每月存款100元,试问经过几过月,小明的存款会超过小李?
答案:5
解答:设经过个月后,小明的存款会超过小李,由题意得:
,解之得,取最小正整数为
答:经过5个月后,小明的存款会超过小李.
分析:根据题目陈述列出不等式,并正确求解,是把文字陈述转化成数学语言的一种基本能力的体现,从而实现了数学的方法解答实际问题,充分体现了学以致用的观点.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 9 页 (共 9 页) 版权所有@21世纪教育网
