第10章数的开方小结与复习 课件(共27张PPT)
文档属性
| 名称 | 第10章数的开方小结与复习 课件(共27张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 676.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-06 17:37:45 | ||
图片预览








文档简介
(共27张PPT)
一、平方根、算术平方根和立方根的概念与性质
概 念 表示 主要性质
平方根
算术
平方根
立方根
若 ,则 x 叫做 a 的平方根.
正数有两个平方根,互为相反数
0 的平方根是 0.负数没有平方根.
若 则x 的非负数值叫做 a 的算术平方根.
非负性:当 a≥0 时, ≥0.
若 ,则 x叫做的立方根.
正数的立方根是一个正数;
负数的立方根是一个负数;
0 的立方根是 0.
联
系 平方根与算术平方根:(1)具有包含关系:平方根包含算术平方根,算术平方根是平方根中的一种;(2)存在条件相同:平方根和算术平方根都只有 才有;(3)0 的平方根、算术平方根均为 .
平方根与立方根:(1)都与相应的乘方运算互为 运算;(2)都可归结为非负数的非负方根来研究.平方根主要通过算术平方根来研究,而负数的立方根也可通过转化为正数的立方根来研究,即 = ;
(3)0 的平方根和立方根都是 0.
非负数
0
逆
二、开平方与开立方
求一个非负数 a 的 的运算,叫做开平方.
其中 a 叫做 .
求一个数 a 的 的运算,叫做开立方.其中 a 叫做 .
开平方与 、开立方与 都分别互为逆运算.
平方根
被开方数
立方根
被开方数
平方
立方
[点拨] (1)求正数的平方根时,往往先求出其算术平方根,再在求出的数前面加上“±”号;
(2)根据平方(立方)运算与开平方(开立方)运算互为逆运算的关系,我们可以通过平方(立方)运算来求一个数的平方根(立方根).
1. 用计算器求一个正数的算术平方根
三、用计算器求算术平方根、立方根
2. 用计算器求立方根
用计算器求一个数 a 的立方根,只需要按书写顺序在计算器上依次键入 .
SHIFT
a
=
a
=
用计算器求一个正数 a 的算术平方根,只需要按书写顺序在计算器上依次键入 .
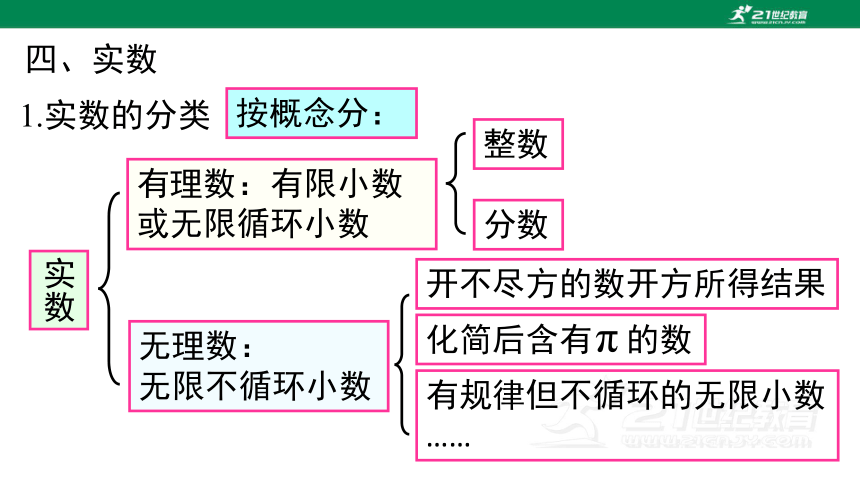
四、实数
1.实数的分类
无理数:
无限不循环小数
有理数:有限小数或无限循环小数
实数
分数
整数
开不尽方的数开方所得结果
有规律但不循环的无限小数
……
化简后含有 的数
按概念分:
正实数
负实数
数实
负有理数
正有理数
按符号分类:
0
负无理数
正无理数
0
正实数
负实数
2. 实数与数轴
(1)实数和数轴上的点是一一对应的关系;
(2)在数轴上表示的两个数,右边的数总比左边的
数大.
3. 在实数范围内,有理数的有关概念、运算法则同样适用.
考点一 平方根、算术平方根及立方根
例1 已知一个正数的两个平方根分别是 a + 3 和 2a - 18,求这个正数.
【解析】根据一个正数的平方根有两个,它们互为相反数,可以得到关于 a 的一元一次方程,解之求得a的值,从而可求出这个正数.
解:根据平方根的性质,有 a + 3 + 2a - 18 = 0,解得 a = 5,a + 3 = 8,8 = 64,所以这个正数是 64.
一个正数的平方根有两个,它们互为相反数.而一个非负数的算术平方根只有一个.另外,一个数的立方根也只有一个,且与它本身的符号相同.
方法总结
2. 的平方根是( )
A. 4 B. 2 C. ±2 D. ±4
1.下列说法正确的有( )
① -64 的立方根是 -4; ② 49 的算术平方根是±7;
③ 的立方根是 ; ④ 的平方根是 .
A. 1 个 B. 2 个 C. 3 个 D. 4 个
B
针对训练
C
例2 若 a,b 为实数且 + |b - 1| = 0,则(ab)2022 = .
【解析】先根据非负数的性质求出 a,b 的值,再根据乘方的定义求出 (ab)2022 的值.
∵ + |b - 1| = 0,
∴ a + 1 = 0,且 b - 1 = 0.
∴ a = -1 ,b = 1.
∴ (ab)2022 = (-1×1)2022 = (-1)2022 = 1. 故填 1.
1
3.若 与 (b - 27)2 互为相反数,则 .
-11
初中阶段主要涉及三种非负数: ≥0,| a |≥0,a2≥0.如果若干个非负数的和为 0,那么这若干个非负数都必为 0.
方法总结
针对训练
例4 在实数 , , 中,分数有 ( )
A. 3 个 B. 2 个 C. 1 个 D. 0 个
C
考点二 无理数的识别
【解析】 是分数; 虽然含有分母 2,但它的分子是无理数 ,所以是无理数;同理 也是无理数. 故选 C.
4 .在实数 π, ,0,-1 中,无理数是( )
A. π B. C. 0 D. -1
A
针对训练
例4 如图,数轴上的点 A,B 分别对应实数 a,b,下列结论正确的是( )
A. a>b B. | a |>| b | C. -a<b D. a + b<0
b
a
0
B
A
C
【解析】数轴上的点表示的数,右边的总比左边的大,故 A 不正确;根据点 A,B 与原点的距离知 | a |<| b |,B 不正确;-a>0,根据 | a |<| b |,知-a<b,C 正确.故选 C.
考点三 实数与数轴上的点的关系
针对训练
5. 若 | a | = -a,则实数 a 在数轴上的对应点一定在( )
A. 原点左侧 B. 原点或原点左侧
C. 原点右侧 D. 原点或原点右侧
B
例5 估计 的值在( )
A. 2 到 3 之间 B. 3 到 4 之间
C. 4 到 5 之间 D. 5 到 6 之间
B
考点四 实数的运算与大小比较
【解析】∵4<6<9,
∴
因此 的值在 3 到 4 之间. 故选 B.
像这类估算无理数的大小的问题,可以将带有根号的无理数的被开方数与已知的平方数作比较,一般的,一个非负数越大,它的算术平方根也越大;也可以利用平方法,将无理数平方后,与已知的平方数作比较.
方法总结
针对训练
6. 满足 的整数 x 是 .
8. 规定用符号 [ x ] 表示一个实数 x 的整数部分,例如:[3.14] = 3, = 0. 按此规定 [ ] 的值为 .
7. 比较大小: .
<
-1,0,1
4
例6 计算 .
【解析】对于被开方数是带分数的,通常需要先将带分数化成假分数,然后再开方.
故填
针对训练
9.计算 .
考点五 本章数学思想和解题方法
分类讨论思想
例7 a 的算术平方根是 3,b 是 16 的平方根,
则 a + b = .
13 或 5
【解析】a 的算术平方根是 3,可知 a = 9;16 的平方根有两个,为±4.由此可以确定 a,b 的值,然后代入计算即可.当 a = 9,b = 4 时,a + b =13;当 a = 9,b = -4 时,a + b = 5.故答案为 13 或 5.
对于该类问题,在求解时,按一定的标准进行分类,并考虑到所有可能的情况,避免漏解或重复.
方法总结
10.若 a 是 16 的平方根,b 是 -27 的立方根,c 的绝对值为 2,求 a - b + c 的值.
针对训练
解:由题意可知 a = 4 或 -4,b = -3,c = 2 或 -2.
(1)当 a = 4,b = -3,c = 2 时,a - b + c = 9;
(2)当 a = -4,b = -3,c = 2 时,a - b + c = 1;
(3)当 a = 4,b = -3,c = -2 时,a - b + c = 5;
(4)当 a = -4,b = -3,c = -2 时,a - b + c = -3.
综上所述,a - b + c 的值为 9 或 1 或 5 或 -3.
数形结合思想
例8 如图,数轴上 A,B 两点对应的实数分别是 1 和 ,若点 A 关于 B 点的对称点为点 C,则点 C 所对应的实数为 .
【解析】设点 C 所对应的实数是 x.根据对称的性质,即对称点到对称中心的距离相等,即可列方程求解即可.设点 C 所对应的实数是 x,则有 x - = -1,解得 x = 2 -1.故答案为 2 -1.
方法总结
数的范围由有理数扩大到实数,实数与数轴上的点建立了一一对应的关系,这样可以通过观察“形”的特点(借助数轴),解答一些关于实数的比较抽象的问题.对于该类问题,运用数形结合思想,先利用数轴表示出三个点的位置,再根据对称的性质解答.
11.数轴上 A,B 两点对应的实数分别是 和 2,若点 A 关于点 B 的对称点为点 C,则点 C 所对应的实数为 .
针对训练
平方根
实 数
数的开方
性质
有理数
整数
无理数
立方根
性质
分数
平方根
算术平方根
立方根
一、平方根、算术平方根和立方根的概念与性质
概 念 表示 主要性质
平方根
算术
平方根
立方根
若 ,则 x 叫做 a 的平方根.
正数有两个平方根,互为相反数
0 的平方根是 0.负数没有平方根.
若 则x 的非负数值叫做 a 的算术平方根.
非负性:当 a≥0 时, ≥0.
若 ,则 x叫做的立方根.
正数的立方根是一个正数;
负数的立方根是一个负数;
0 的立方根是 0.
联
系 平方根与算术平方根:(1)具有包含关系:平方根包含算术平方根,算术平方根是平方根中的一种;(2)存在条件相同:平方根和算术平方根都只有 才有;(3)0 的平方根、算术平方根均为 .
平方根与立方根:(1)都与相应的乘方运算互为 运算;(2)都可归结为非负数的非负方根来研究.平方根主要通过算术平方根来研究,而负数的立方根也可通过转化为正数的立方根来研究,即 = ;
(3)0 的平方根和立方根都是 0.
非负数
0
逆
二、开平方与开立方
求一个非负数 a 的 的运算,叫做开平方.
其中 a 叫做 .
求一个数 a 的 的运算,叫做开立方.其中 a 叫做 .
开平方与 、开立方与 都分别互为逆运算.
平方根
被开方数
立方根
被开方数
平方
立方
[点拨] (1)求正数的平方根时,往往先求出其算术平方根,再在求出的数前面加上“±”号;
(2)根据平方(立方)运算与开平方(开立方)运算互为逆运算的关系,我们可以通过平方(立方)运算来求一个数的平方根(立方根).
1. 用计算器求一个正数的算术平方根
三、用计算器求算术平方根、立方根
2. 用计算器求立方根
用计算器求一个数 a 的立方根,只需要按书写顺序在计算器上依次键入 .
SHIFT
a
=
a
=
用计算器求一个正数 a 的算术平方根,只需要按书写顺序在计算器上依次键入 .
四、实数
1.实数的分类
无理数:
无限不循环小数
有理数:有限小数或无限循环小数
实数
分数
整数
开不尽方的数开方所得结果
有规律但不循环的无限小数
……
化简后含有 的数
按概念分:
正实数
负实数
数实
负有理数
正有理数
按符号分类:
0
负无理数
正无理数
0
正实数
负实数
2. 实数与数轴
(1)实数和数轴上的点是一一对应的关系;
(2)在数轴上表示的两个数,右边的数总比左边的
数大.
3. 在实数范围内,有理数的有关概念、运算法则同样适用.
考点一 平方根、算术平方根及立方根
例1 已知一个正数的两个平方根分别是 a + 3 和 2a - 18,求这个正数.
【解析】根据一个正数的平方根有两个,它们互为相反数,可以得到关于 a 的一元一次方程,解之求得a的值,从而可求出这个正数.
解:根据平方根的性质,有 a + 3 + 2a - 18 = 0,解得 a = 5,a + 3 = 8,8 = 64,所以这个正数是 64.
一个正数的平方根有两个,它们互为相反数.而一个非负数的算术平方根只有一个.另外,一个数的立方根也只有一个,且与它本身的符号相同.
方法总结
2. 的平方根是( )
A. 4 B. 2 C. ±2 D. ±4
1.下列说法正确的有( )
① -64 的立方根是 -4; ② 49 的算术平方根是±7;
③ 的立方根是 ; ④ 的平方根是 .
A. 1 个 B. 2 个 C. 3 个 D. 4 个
B
针对训练
C
例2 若 a,b 为实数且 + |b - 1| = 0,则(ab)2022 = .
【解析】先根据非负数的性质求出 a,b 的值,再根据乘方的定义求出 (ab)2022 的值.
∵ + |b - 1| = 0,
∴ a + 1 = 0,且 b - 1 = 0.
∴ a = -1 ,b = 1.
∴ (ab)2022 = (-1×1)2022 = (-1)2022 = 1. 故填 1.
1
3.若 与 (b - 27)2 互为相反数,则 .
-11
初中阶段主要涉及三种非负数: ≥0,| a |≥0,a2≥0.如果若干个非负数的和为 0,那么这若干个非负数都必为 0.
方法总结
针对训练
例4 在实数 , , 中,分数有 ( )
A. 3 个 B. 2 个 C. 1 个 D. 0 个
C
考点二 无理数的识别
【解析】 是分数; 虽然含有分母 2,但它的分子是无理数 ,所以是无理数;同理 也是无理数. 故选 C.
4 .在实数 π, ,0,-1 中,无理数是( )
A. π B. C. 0 D. -1
A
针对训练
例4 如图,数轴上的点 A,B 分别对应实数 a,b,下列结论正确的是( )
A. a>b B. | a |>| b | C. -a<b D. a + b<0
b
a
0
B
A
C
【解析】数轴上的点表示的数,右边的总比左边的大,故 A 不正确;根据点 A,B 与原点的距离知 | a |<| b |,B 不正确;-a>0,根据 | a |<| b |,知-a<b,C 正确.故选 C.
考点三 实数与数轴上的点的关系
针对训练
5. 若 | a | = -a,则实数 a 在数轴上的对应点一定在( )
A. 原点左侧 B. 原点或原点左侧
C. 原点右侧 D. 原点或原点右侧
B
例5 估计 的值在( )
A. 2 到 3 之间 B. 3 到 4 之间
C. 4 到 5 之间 D. 5 到 6 之间
B
考点四 实数的运算与大小比较
【解析】∵4<6<9,
∴
因此 的值在 3 到 4 之间. 故选 B.
像这类估算无理数的大小的问题,可以将带有根号的无理数的被开方数与已知的平方数作比较,一般的,一个非负数越大,它的算术平方根也越大;也可以利用平方法,将无理数平方后,与已知的平方数作比较.
方法总结
针对训练
6. 满足 的整数 x 是 .
8. 规定用符号 [ x ] 表示一个实数 x 的整数部分,例如:[3.14] = 3, = 0. 按此规定 [ ] 的值为 .
7. 比较大小: .
<
-1,0,1
4
例6 计算 .
【解析】对于被开方数是带分数的,通常需要先将带分数化成假分数,然后再开方.
故填
针对训练
9.计算 .
考点五 本章数学思想和解题方法
分类讨论思想
例7 a 的算术平方根是 3,b 是 16 的平方根,
则 a + b = .
13 或 5
【解析】a 的算术平方根是 3,可知 a = 9;16 的平方根有两个,为±4.由此可以确定 a,b 的值,然后代入计算即可.当 a = 9,b = 4 时,a + b =13;当 a = 9,b = -4 时,a + b = 5.故答案为 13 或 5.
对于该类问题,在求解时,按一定的标准进行分类,并考虑到所有可能的情况,避免漏解或重复.
方法总结
10.若 a 是 16 的平方根,b 是 -27 的立方根,c 的绝对值为 2,求 a - b + c 的值.
针对训练
解:由题意可知 a = 4 或 -4,b = -3,c = 2 或 -2.
(1)当 a = 4,b = -3,c = 2 时,a - b + c = 9;
(2)当 a = -4,b = -3,c = 2 时,a - b + c = 1;
(3)当 a = 4,b = -3,c = -2 时,a - b + c = 5;
(4)当 a = -4,b = -3,c = -2 时,a - b + c = -3.
综上所述,a - b + c 的值为 9 或 1 或 5 或 -3.
数形结合思想
例8 如图,数轴上 A,B 两点对应的实数分别是 1 和 ,若点 A 关于 B 点的对称点为点 C,则点 C 所对应的实数为 .
【解析】设点 C 所对应的实数是 x.根据对称的性质,即对称点到对称中心的距离相等,即可列方程求解即可.设点 C 所对应的实数是 x,则有 x - = -1,解得 x = 2 -1.故答案为 2 -1.
方法总结
数的范围由有理数扩大到实数,实数与数轴上的点建立了一一对应的关系,这样可以通过观察“形”的特点(借助数轴),解答一些关于实数的比较抽象的问题.对于该类问题,运用数形结合思想,先利用数轴表示出三个点的位置,再根据对称的性质解答.
11.数轴上 A,B 两点对应的实数分别是 和 2,若点 A 关于点 B 的对称点为点 C,则点 C 所对应的实数为 .
针对训练
平方根
实 数
数的开方
性质
有理数
整数
无理数
立方根
性质
分数
平方根
算术平方根
立方根
