10.2实数(2) 课件(共22张PPT)
文档属性
| 名称 | 10.2实数(2) 课件(共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 736.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-06 17:39:04 | ||
图片预览








文档简介
(共22张PPT)
(1)用计算器求 ;
(2)利用平方运算验算(1)中所得的结果.
=1.414213562373095048801688724209698078569671875376948073176679737990732478462107038850387534327641572735013846230912297024924836055850737212644121497099935831413222665927505592755799950501152782060571470109559971605970274···
用计算机计算,你可能会大吃一惊:
那么, 是怎样的数呢?
我们知道,有理数包括整数和分数,而任何一个分数写成小数的形式,必定是有限小数或者无限循环小数,例如:
请你随意写出三个分数,将它化成小数,验证这个结论.
在数学上已经证明,没有一个有理数的平方等于 2,也就是说, 不是一个有理数.
不是一个有理数,实际上,它是一个无限不循环小数.
类似地, 、圆周率 等也都不是有理数,它们都是无限不循环小数.
定义:无限不循环的小数叫做无理数.
无理数的概念
例1 判断下列数哪些是有理数?哪些是无理数?
典例精析
有理数是:
无理数是:
解:
1.圆周率 及一些含有 的数
2.开方开不尽的数,如:
3.有一定的规律,但不循环的无限小数,如:
无理数的特征:
注意:带根号的数不一定是无理数
判定一个数是不是无理数:
(1)是看它是不是无限小数;
(2)看它是不是不循环小数;
(3)所有的有理数都能写成分数形式,但无理数则不能.
归纳总结
具体从以下几方面来判断:
(1)开方开不尽的数是无理数;
(2) π 是无理数;
(3)无理数与有理数的和、差一定是无理数;
(4)无理数与有理数(不为 0)的积、商一定是无理数.
有理数和无理数统称为实数.
按概念分类:
无理数:
无限不循环小数
有理数:可以写成
有限小数或无限循环小数
实 数
分数
整数
开不尽方的数开方所得结果;
有规律但不循环的无限小数;
……
化简后含有 π 的数;
实数的概念及分类
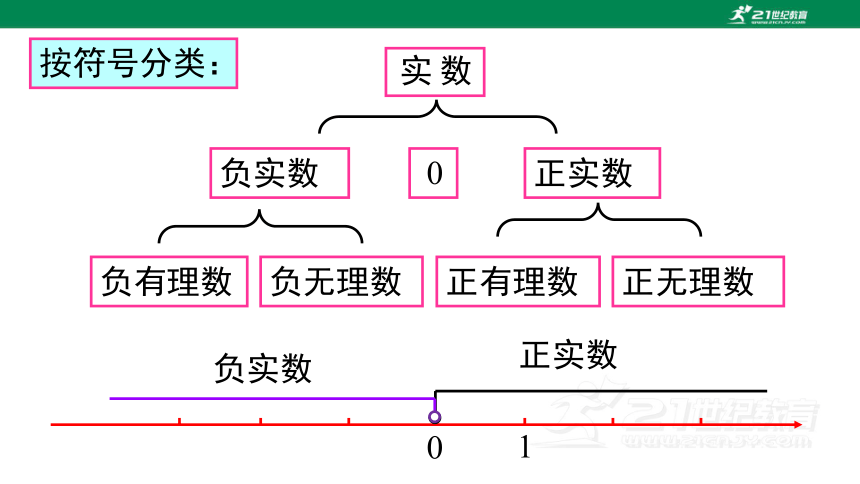
正实数
负实数
数实
负有理数
正有理数
按符号分类:
0
负无理数
正无理数
0
正实数
1
负实数
在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样.有理数的运算法则及运算律对实数仍然适用.例如:
与 互为相反数
与 互为倒数
=?
1
1
将两个边长为 1 的正方形剪拼成一个大正方形.
你能在数轴上找到表示 的点吗?
a
探究:
实数与数轴上点的关系
0
1
-1
在数轴上找表示 的点
数轴上的任一点必定表示一个实数;反过来,每一个实数(有理数或无理数)也都可以用数轴上的一个点来表示.
即:实数与数轴上的点一一对应.
归纳总结
例2 把下列实数表示在数轴上,并比较它们的大小.
(用“<”号连接)
解: 如图所示.
-2
1.5
在数轴上表示的两个数,右边的数总比左边的数大.
例3 试比较 与 π 的大小关系.
解:用计算器求得
而
这样,容易判断
实数的大小比较和运算,通常可取它们的近似值来进行.
例4 计算: . (结果精确到0.01)
解: 用计算器求得
于是
所以
一、判断
1.实数不是有理数就是无理数.( )
2.无理数都是无限不循环小数.( )
3.无理数都是无限小数.( )
4.带根号的数都是无理数.( )
×
5.无理数一定都带根号.( )
6.两个无理数之积不一定是无理数.( )
7.两个无理数之和一定是无理数.( )
8.数轴上的任何一点都可以表示实数.( )
×
×
2. 的相反数是 ,绝对值是 .
3.绝对值等于 的数是 , 的平方是 .
二、填空与选择
1.正实数的绝对值是 ,0 的绝对值是 ,
负实数的绝对值是 .
它本身
0
它的相反数
4.比较大小:-7 .
<
5.一个数的绝对值是 ,则这个数是 .
6.(金华·中考)在 -3,- , -1, 0 这四个实数中,最大的是( )
A. -3 B.- C. -1 D. 0
【解析】因为-3,- ,-1为负数,都小于 0,所以 0 最大.
答案:D
D
7.如图,在数轴上点 A 和点 B 之间的整数是 .
【解析】1< <2,2< <3,在 与 之间
的整数是 2.
答案:2
A
B
2
实数
有理数和无理数统称实数
在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样.
实数与数轴上点的一一对应
(1)用计算器求 ;
(2)利用平方运算验算(1)中所得的结果.
=1.414213562373095048801688724209698078569671875376948073176679737990732478462107038850387534327641572735013846230912297024924836055850737212644121497099935831413222665927505592755799950501152782060571470109559971605970274···
用计算机计算,你可能会大吃一惊:
那么, 是怎样的数呢?
我们知道,有理数包括整数和分数,而任何一个分数写成小数的形式,必定是有限小数或者无限循环小数,例如:
请你随意写出三个分数,将它化成小数,验证这个结论.
在数学上已经证明,没有一个有理数的平方等于 2,也就是说, 不是一个有理数.
不是一个有理数,实际上,它是一个无限不循环小数.
类似地, 、圆周率 等也都不是有理数,它们都是无限不循环小数.
定义:无限不循环的小数叫做无理数.
无理数的概念
例1 判断下列数哪些是有理数?哪些是无理数?
典例精析
有理数是:
无理数是:
解:
1.圆周率 及一些含有 的数
2.开方开不尽的数,如:
3.有一定的规律,但不循环的无限小数,如:
无理数的特征:
注意:带根号的数不一定是无理数
判定一个数是不是无理数:
(1)是看它是不是无限小数;
(2)看它是不是不循环小数;
(3)所有的有理数都能写成分数形式,但无理数则不能.
归纳总结
具体从以下几方面来判断:
(1)开方开不尽的数是无理数;
(2) π 是无理数;
(3)无理数与有理数的和、差一定是无理数;
(4)无理数与有理数(不为 0)的积、商一定是无理数.
有理数和无理数统称为实数.
按概念分类:
无理数:
无限不循环小数
有理数:可以写成
有限小数或无限循环小数
实 数
分数
整数
开不尽方的数开方所得结果;
有规律但不循环的无限小数;
……
化简后含有 π 的数;
实数的概念及分类
正实数
负实数
数实
负有理数
正有理数
按符号分类:
0
负无理数
正无理数
0
正实数
1
负实数
在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样.有理数的运算法则及运算律对实数仍然适用.例如:
与 互为相反数
与 互为倒数
=?
1
1
将两个边长为 1 的正方形剪拼成一个大正方形.
你能在数轴上找到表示 的点吗?
a
探究:
实数与数轴上点的关系
0
1
-1
在数轴上找表示 的点
数轴上的任一点必定表示一个实数;反过来,每一个实数(有理数或无理数)也都可以用数轴上的一个点来表示.
即:实数与数轴上的点一一对应.
归纳总结
例2 把下列实数表示在数轴上,并比较它们的大小.
(用“<”号连接)
解: 如图所示.
-2
1.5
在数轴上表示的两个数,右边的数总比左边的数大.
例3 试比较 与 π 的大小关系.
解:用计算器求得
而
这样,容易判断
实数的大小比较和运算,通常可取它们的近似值来进行.
例4 计算: . (结果精确到0.01)
解: 用计算器求得
于是
所以
一、判断
1.实数不是有理数就是无理数.( )
2.无理数都是无限不循环小数.( )
3.无理数都是无限小数.( )
4.带根号的数都是无理数.( )
×
5.无理数一定都带根号.( )
6.两个无理数之积不一定是无理数.( )
7.两个无理数之和一定是无理数.( )
8.数轴上的任何一点都可以表示实数.( )
×
×
2. 的相反数是 ,绝对值是 .
3.绝对值等于 的数是 , 的平方是 .
二、填空与选择
1.正实数的绝对值是 ,0 的绝对值是 ,
负实数的绝对值是 .
它本身
0
它的相反数
4.比较大小:-7 .
<
5.一个数的绝对值是 ,则这个数是 .
6.(金华·中考)在 -3,- , -1, 0 这四个实数中,最大的是( )
A. -3 B.- C. -1 D. 0
【解析】因为-3,- ,-1为负数,都小于 0,所以 0 最大.
答案:D
D
7.如图,在数轴上点 A 和点 B 之间的整数是 .
【解析】1< <2,2< <3,在 与 之间
的整数是 2.
答案:2
A
B
2
实数
有理数和无理数统称实数
在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样.
实数与数轴上点的一一对应
