12.5.3角平分线(1) 课件(共38张PPT)
文档属性
| 名称 | 12.5.3角平分线(1) 课件(共38张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-06 17:52:21 | ||
图片预览









文档简介
(共38张PPT)
逐点
导讲练
课堂小结
作业提升
课时讲解
1
课时流程
2
角平分线的性质定理
角平分线的判定定理
三角形的角平分线的性质(拓展点)
知1-讲
知识点
角平分线的性质定理
1
1. 性质定理 角平分线上的点到角两边的距离相等 .
角平分线的性质的两个必要条件:
(1)点在角平分线上;
(2)这个点到角两边的距离即点到角两边的垂线段的长度 . 两者缺一不可 .
知1-讲
特别提醒
1. 角平分线的性质是由两个条件(角平分线,垂线)得到一个结论(线段相等).
2. 利用角平分线的性质证明线段相等时,证明的线段是“垂直于角两边的线段”而不是“垂直于角平分线的线段”.
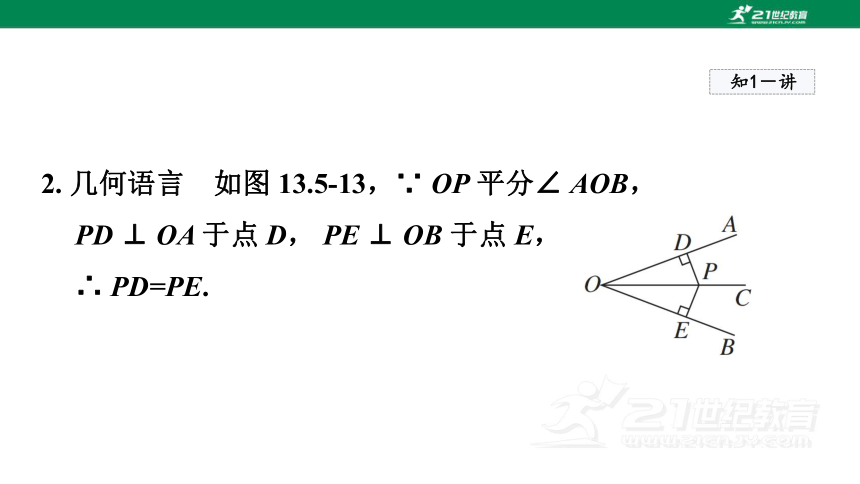
2. 几何语言 如图 13.5-13,∵ OP 平分∠ AOB,
PD ⊥ OA 于点 D, PE ⊥ OB 于点 E,
∴ PD=PE.
知1-讲
知1-练
如图 13.5-14, OD 平分∠ EOF,在 OE、 OF 上分别取点 A、 B, 使 OA=OB, P 为 OD 上 一 点, PM ⊥ BD,PN ⊥ AD,垂足分别为 M、 N.
求证: PM=PN.
例1
知1-练
解题秘方:在图中找出符合角平分线的性质的模型,利用角平分线的性质证线段相等 .
知1-练
知1-练
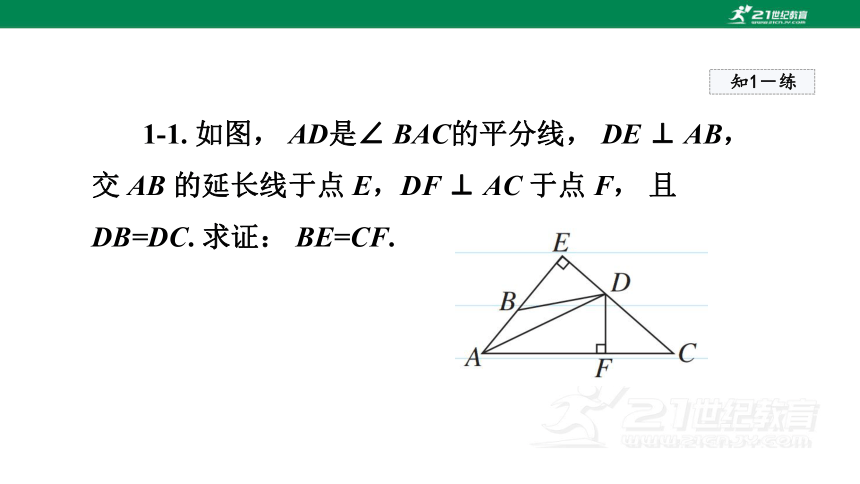
1-1. 如图, AD是∠ BAC的平分线, DE ⊥ AB,交 AB 的延长线于点 E,DF ⊥ AC 于点 F, 且DB=DC. 求证: BE=CF.
知1-练
知1-练
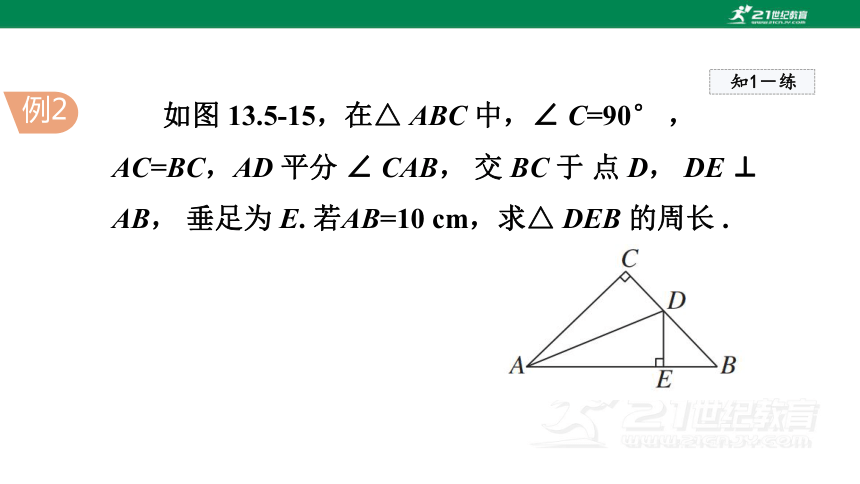
如图 13.5-15,在△ ABC 中,∠ C=90° , AC=BC,AD 平分 ∠ CAB, 交 BC 于 点 D, DE ⊥ AB, 垂足为 E. 若AB=10 cm,求△ DEB 的周长 .
例2
知1-练
解题秘方:运用角平分线的性质及全等三角形的性质,将△ DEB 的周长转化为线段 AB 的长 .
知1-练
知1-练
解法提醒:求三角形的周长时,若三角形各边的长不易求解,可考虑找出题中的相等线段进行等量替换,而角平分线的性质能起到等量替换的作用,使三角形的周长等于一条线段长,从而整体求出 .
知1-练
2-1.如图, 在 △ ABC中, ∠ C=90 ° , AD 平分 ∠ BAC, DE ⊥ AB于点 E.
有下列结论:① CD=ED;② AC+BE=AB;
③∠ BDE= ∠ BAC;④ DA 平分∠ CDE.
其中正确的结论的个数是( )
A. 1 B. 2 C. 3 D. 4
D
知1-练
如图 13.5-16, BD 是△ ABC 的角平分线, DE ⊥ AB于点 E, S △ ABC=90 cm2, AB=18 cm, BC=12 cm,求 DE 的长 .
例3
知1-练
解题秘方:紧扣总面积等于各部分面积的和求解 .
知1-练
3-1. [ 中考·北京 ] 如图,在△ ABC 中, AD 平分∠ BAC, DE ⊥ AB. 若AC=2, DE=1,则
S△ ACD=____________.
1
知2-讲
知识点
角平分线的判定定理
2
1.判定定理 角的内部到角两边距离相等的点在角的平分线上 .
知2-讲
2. 几何语言 如图 13.5-17 所示 .
∵ 点 P 为 ∠ AOB 内 一 点, PD ⊥ OA,
PE ⊥ OB,垂足分别为 D、 E,且 PD=PE,
∴点 P 在∠ AOB 的平分线 OC 上 .
知2-讲
特别提醒
1. 使用该判定定理的前提是这个点必须在角的内部 .
2. 角平分线的判定是由两个条件(垂线,线段相等)得到一个结论(角平分线).
3. 角平分线的判定定理是证明两角相等的重要依据,它比利用三角形全等证两角相等更方便快捷 .
知2-讲
知2-练
如图 13.5-18, BE=CF, BF ⊥ AC 于点 F, CE ⊥ AB于点 E, BF 和 CE 交于点 D.
求证: AD 平分∠ BAC.
例4
知2-练
解题秘方:利用角平分线的判定定理证明角平分线时,紧扣点在角的内部且点到角两边的距离相等进行证明 .
知2-练
知2-练
方法点拨:证明角平分线的方法思路:
1. 从数量上证明被角平分线分成的两个角相等 .
2. 从形状上证明角的内部的点到角两边的距离相等,即只需从要证的线上的某一点向角的两边作垂线段,再证明垂线段相等即可.这样把证“某线是角的平分线”的问题转化为证“垂线段相等”的问题,体现了转化思想 .
知2-练
4-1.如图,在△ ABC中,BD ⊥ AC 于 D, CE ⊥AB 于 E, 且 BO=CO.
求证: AO 平分∠ BAC.
知2-练
知2-练
4-2.如图, D、 E、 F 分别是 △ ABC 三边上的点, CE=BF,△ DCE 和△ DBF 的面积相等 .
求证: AD 平分∠ BAC.
知2-练
知3-讲
知识点
三角形的角平分线的性质(拓展点)
3
1.性质定理 三角形的三条角平分线交于一点,并且这一点到三条边的距离相等 . 这一点叫三角形的内心 .
知3-讲
2. 几何语言 如图 13.5-19, 在 △ ABC 中,
AD、 BM、 CN 分别是 ∠ BAC、 ∠ ABC、
∠ ACB 的平分线, AD、 BM、 CN 交于一点 O,
且点 O 到三边 BC、 AB、 AC 的距离( OE、
OG、 OF 的长)相等,即 OE=OG=OF.
知3-讲
要点解读
三角形的三条角平分线相交于三角形内一点,且该点到三角形三边的距离相等 . 反之,三角形内部到三边距离相等的点是三角形三条角平分线的交点 .
知3-练
如图 13.5-20, 在 △ ABC 中, 点 O 是 ∠ ABC,∠ ACB 的平分线的交点, AB+BC+AC=20. 过 O 作 OD ⊥ BC于点 D,且 OD=3,求△ ABC 的面积 .
例5
知3-练
解题秘方:紧扣三角形内角平分线的性质,即角平分线上的点到角两边的距离相等解题 .
知3-练
知3-练
5-1.如图 . 有一块三角形的空地 ABC,其三边长 AB、 AC、 BC 分别为30m、 40 m、 50 m. 现要把它分成面积比为 3∶ 4∶ 5的三部分种植三种不同的花,请你设计一种方案,并简要说明理由 .
知3-练
解:方案如图所示.(方案不唯一)
分别作∠ABC和∠ACB的平分线,两线交于点P,连结AP,则△ABP,△ACP,△BCP即为所求的三块地.
理由:易知P为△ABC的三个内角平分线的交点,∴点P到AB、AC、BC的距离均相等.
∴△ABP、△ACP、△BCP的面积
比即为它们的底边AB、AC、BC的长度的比.
即△ABP、△ACP、△BCP的面积比为3∶4∶5.
角平分线
三角形的
角平分线
角平
分线
性质
判定
逐点
导讲练
课堂小结
作业提升
课时讲解
1
课时流程
2
角平分线的性质定理
角平分线的判定定理
三角形的角平分线的性质(拓展点)
知1-讲
知识点
角平分线的性质定理
1
1. 性质定理 角平分线上的点到角两边的距离相等 .
角平分线的性质的两个必要条件:
(1)点在角平分线上;
(2)这个点到角两边的距离即点到角两边的垂线段的长度 . 两者缺一不可 .
知1-讲
特别提醒
1. 角平分线的性质是由两个条件(角平分线,垂线)得到一个结论(线段相等).
2. 利用角平分线的性质证明线段相等时,证明的线段是“垂直于角两边的线段”而不是“垂直于角平分线的线段”.
2. 几何语言 如图 13.5-13,∵ OP 平分∠ AOB,
PD ⊥ OA 于点 D, PE ⊥ OB 于点 E,
∴ PD=PE.
知1-讲
知1-练
如图 13.5-14, OD 平分∠ EOF,在 OE、 OF 上分别取点 A、 B, 使 OA=OB, P 为 OD 上 一 点, PM ⊥ BD,PN ⊥ AD,垂足分别为 M、 N.
求证: PM=PN.
例1
知1-练
解题秘方:在图中找出符合角平分线的性质的模型,利用角平分线的性质证线段相等 .
知1-练
知1-练
1-1. 如图, AD是∠ BAC的平分线, DE ⊥ AB,交 AB 的延长线于点 E,DF ⊥ AC 于点 F, 且DB=DC. 求证: BE=CF.
知1-练
知1-练
如图 13.5-15,在△ ABC 中,∠ C=90° , AC=BC,AD 平分 ∠ CAB, 交 BC 于 点 D, DE ⊥ AB, 垂足为 E. 若AB=10 cm,求△ DEB 的周长 .
例2
知1-练
解题秘方:运用角平分线的性质及全等三角形的性质,将△ DEB 的周长转化为线段 AB 的长 .
知1-练
知1-练
解法提醒:求三角形的周长时,若三角形各边的长不易求解,可考虑找出题中的相等线段进行等量替换,而角平分线的性质能起到等量替换的作用,使三角形的周长等于一条线段长,从而整体求出 .
知1-练
2-1.如图, 在 △ ABC中, ∠ C=90 ° , AD 平分 ∠ BAC, DE ⊥ AB于点 E.
有下列结论:① CD=ED;② AC+BE=AB;
③∠ BDE= ∠ BAC;④ DA 平分∠ CDE.
其中正确的结论的个数是( )
A. 1 B. 2 C. 3 D. 4
D
知1-练
如图 13.5-16, BD 是△ ABC 的角平分线, DE ⊥ AB于点 E, S △ ABC=90 cm2, AB=18 cm, BC=12 cm,求 DE 的长 .
例3
知1-练
解题秘方:紧扣总面积等于各部分面积的和求解 .
知1-练
3-1. [ 中考·北京 ] 如图,在△ ABC 中, AD 平分∠ BAC, DE ⊥ AB. 若AC=2, DE=1,则
S△ ACD=____________.
1
知2-讲
知识点
角平分线的判定定理
2
1.判定定理 角的内部到角两边距离相等的点在角的平分线上 .
知2-讲
2. 几何语言 如图 13.5-17 所示 .
∵ 点 P 为 ∠ AOB 内 一 点, PD ⊥ OA,
PE ⊥ OB,垂足分别为 D、 E,且 PD=PE,
∴点 P 在∠ AOB 的平分线 OC 上 .
知2-讲
特别提醒
1. 使用该判定定理的前提是这个点必须在角的内部 .
2. 角平分线的判定是由两个条件(垂线,线段相等)得到一个结论(角平分线).
3. 角平分线的判定定理是证明两角相等的重要依据,它比利用三角形全等证两角相等更方便快捷 .
知2-讲
知2-练
如图 13.5-18, BE=CF, BF ⊥ AC 于点 F, CE ⊥ AB于点 E, BF 和 CE 交于点 D.
求证: AD 平分∠ BAC.
例4
知2-练
解题秘方:利用角平分线的判定定理证明角平分线时,紧扣点在角的内部且点到角两边的距离相等进行证明 .
知2-练
知2-练
方法点拨:证明角平分线的方法思路:
1. 从数量上证明被角平分线分成的两个角相等 .
2. 从形状上证明角的内部的点到角两边的距离相等,即只需从要证的线上的某一点向角的两边作垂线段,再证明垂线段相等即可.这样把证“某线是角的平分线”的问题转化为证“垂线段相等”的问题,体现了转化思想 .
知2-练
4-1.如图,在△ ABC中,BD ⊥ AC 于 D, CE ⊥AB 于 E, 且 BO=CO.
求证: AO 平分∠ BAC.
知2-练
知2-练
4-2.如图, D、 E、 F 分别是 △ ABC 三边上的点, CE=BF,△ DCE 和△ DBF 的面积相等 .
求证: AD 平分∠ BAC.
知2-练
知3-讲
知识点
三角形的角平分线的性质(拓展点)
3
1.性质定理 三角形的三条角平分线交于一点,并且这一点到三条边的距离相等 . 这一点叫三角形的内心 .
知3-讲
2. 几何语言 如图 13.5-19, 在 △ ABC 中,
AD、 BM、 CN 分别是 ∠ BAC、 ∠ ABC、
∠ ACB 的平分线, AD、 BM、 CN 交于一点 O,
且点 O 到三边 BC、 AB、 AC 的距离( OE、
OG、 OF 的长)相等,即 OE=OG=OF.
知3-讲
要点解读
三角形的三条角平分线相交于三角形内一点,且该点到三角形三边的距离相等 . 反之,三角形内部到三边距离相等的点是三角形三条角平分线的交点 .
知3-练
如图 13.5-20, 在 △ ABC 中, 点 O 是 ∠ ABC,∠ ACB 的平分线的交点, AB+BC+AC=20. 过 O 作 OD ⊥ BC于点 D,且 OD=3,求△ ABC 的面积 .
例5
知3-练
解题秘方:紧扣三角形内角平分线的性质,即角平分线上的点到角两边的距离相等解题 .
知3-练
知3-练
5-1.如图 . 有一块三角形的空地 ABC,其三边长 AB、 AC、 BC 分别为30m、 40 m、 50 m. 现要把它分成面积比为 3∶ 4∶ 5的三部分种植三种不同的花,请你设计一种方案,并简要说明理由 .
知3-练
解:方案如图所示.(方案不唯一)
分别作∠ABC和∠ACB的平分线,两线交于点P,连结AP,则△ABP,△ACP,△BCP即为所求的三块地.
理由:易知P为△ABC的三个内角平分线的交点,∴点P到AB、AC、BC的距离均相等.
∴△ABP、△ACP、△BCP的面积
比即为它们的底边AB、AC、BC的长度的比.
即△ABP、△ACP、△BCP的面积比为3∶4∶5.
角平分线
三角形的
角平分线
角平
分线
性质
判定
