14.2数据的表示 课件(共39张PPT)
文档属性
| 名称 | 14.2数据的表示 课件(共39张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-06 17:54:28 | ||
图片预览











文档简介
(共39张PPT)
逐点
导讲练
课堂小结
作业提升
课时讲解
1
课时流程
2
扇形统计图
利用统计图表传递信息
知1-讲
知识点
扇形统计图
1
1.扇形统计图 扇形统计图是用整个圆代表所研究的总体,用圆中各个扇形代表组成总体的各个部分 .
特别提醒: 扇形统计图中各部分在总体中所占百分比之和为 1(有时由于计算过程中四舍五入的原因,实际百分比之和并不刚好等于 1),与圆的大小无关 .
知1-讲
特别解读
1. 在同一个扇形统计图中,扇形圆心角的度数越大,相应的扇形面积也越大,该部分占总体的百分比也就越大;反之,则越小 .
2. 扇形统计图一般有两种形式:一种以百分比的形式出现;另一种以度数的形式出现 . 根据具体题目,可通过百分比求出相应部分的圆心角度数,同样也可根据圆心角度数求出相应的百分比 .
2. 优缺点 扇形统计图的优点是可以看出被统计对象所占总数量的百分比,缺点是不能从统计图中看出具体的数量 .
知1-讲
3. 制作扇形统计图的一般步骤
(1)计算出各部分在总体中所占的百分比;
(2)用 360°乘各部分在总体中所占的百分比,计算出各部分所对应的扇形圆心角的度数;
(3)以适当长为半径画圆,根据算出的各圆心角的度数画出各扇形;
(4)在每个扇形上注明相应的名称和百分比,各部分的名称可以注在图上,也可用图例标明 .
知1-讲
知1-练
[ 中考·达州 ]某校在今年“五· 四”开展了“好书伴我成长”的读书活动.为了解八年级 450 名学生的读书情况,随机调查了八年级 50 名学生本学期读书册数,并将统计数据制成了扇形统计图,如图 15.2-1,则该校八年级学生读书册数等于 3 册的约有_____ 名 .
例1
知1-练
解题秘方:紧扣扇形统计图中的基本特征,求出未知部分的百分比 . 再算出未知部分的数量 .
知1-练
解:由扇形统计图可知,随机调查的八年级 50 名学生中读书册数等于 3 册的学生人数所占的百分比为 1- 6% - 24% - 30% - 6%=34%,即 m%=34%,
所以该校八年级学生读书册数等于 3 册的约有 450×34%=153(名) .
答案:153
知1-练
1-1. [ 中考·温州 ] 某校参加课外兴趣小组的学生人数统计图如图所示 . 若信息技术小组有 60 人,则劳动实践小组有( )
A. 75 人 B. 90 人
C. 108 人 D. 150 人
B
知1-练
某校准备搬迁到新校舍,在迁入新校舍前,同学们就该校 300 名学生如何到校问题进行了一次调查,并得到下列数据:步行 60 人,骑自行车 100 人,坐公共汽车 130 人,其他 10 人,将上面的数据制成扇形统计图 .
例2
知1-练
解题秘方:紧扣绘制扇形统计图的步骤,先求出各部分所占的百分比,再计算各部分所对应扇形的圆心角的度数,最后绘制扇形统计图 .
知1-练
感悟新知
解:由题中数据列表:
由表中数据直接绘制扇形统计图,
如图 15.2-2 所示 .
到校方式 步行 骑自行车 坐公共汽车 其他
人数 60 100 130 10
百分比 20% 33.3% 43.3% 3.4%
圆心角度数 72° 120° 156° 12°
知1-练
2-1.下表是对某中学八(4)班的同学就“父母回家后,你会主动给他们倒一杯水吗”的调查结果 . 请你按要求用扇形统计图表示该调查的结果 .
项目 主动 倒水 偶尔 倒水 不倒水
人数 27 18 15
项目 主动 倒水 偶尔 倒水 不倒水
百分比
圆心角 度数
知1-练
(1)计算各部分人数所占百分比及扇形各个圆心角的度数,并填入下表:
45% 30% 25%
162° 108° 90°
知1-练
(2)制作扇形统计图,并标上百分比 .
解:对某中学八(4)班的同学就“父母回家后,你会主动给他们倒一杯水吗”的调查结果制作扇形统计图如图所示.
知2-讲
知识点
利用统计图表传递信息
2
数据的描述方法有统计表和统计图两种
(1) 统计表的作用:
①使数据更直观、清楚,便于分析;
②用数据把研究对象之间的变化规律清楚地表示出来;
③用数据把研究对象之间的差别清楚地表示出来,以便
于人们分析问题和研究问题 .
知2-讲
(2)统计图的作用:
统计图 条形统计图 折线统计图 扇形统计图
特点 用一个单位长度表示一定的数量,用直条的高低表示数量的多少 用一个单位长度表示一定的数量,用折线的起伏表示数 量的增减变化 用整个圆表示总体,用圆中各个扇形表 示总体的各个部分
知2-讲
图例
知2-讲
作用 能清楚地表示每个项目的具体数目,便于相互比较 能清楚地看出数量增减变化的情况,也能看出各数量的多少 能清楚地表示各部分在总体中所占的百分比
选用 表示数据的数量特征时 表示数据的发展变化趋势时 表示各部分数据占总体的百分比时
知2-讲
特别解读
1. 分析条形统计图、折线统计图时,首先要看统计图的横轴和纵轴分别代表什么量;分析扇形统计图时,根据各部分所占百分比或各部分所对应的扇形的圆心角度数来分析解答.
2. 绘制统计图时,根据绘图的一般步骤进行绘制 .
知2-练
高叔叔在池塘里养了许多鱼,各种鱼的数量如图15.2-3,下列说法正确的是( )
A. 草鱼的条数比鲢鱼多
B. 鲤鱼在所有鱼中所占比例最小
C. 鲢鱼在所有鱼中所占比例最大
D. 鲫鱼的条数最多
例3
知2-练
答案:D
解题秘方:紧扣条形统计图的特点,利用条形统计图提供的数据信息进行判断 .
解:由直条的高度可知鲫鱼条数最多,其次是鲢鱼、鲤鱼,草鱼最少,故草鱼的条数比鲢鱼少,选项 A 错误;在所有鱼中所占比例最小的是草鱼,所占比例最大的是鲫鱼,故选项 B、C 错误 .
知2-练
3-1. [ 中考·徐州 ] 第七次全国人口普查的部分结果如图所示 .根据该统计图,下列判断错误的是( )
A.徐州 0~14 岁人口比重高于全国
B.徐州 15~59 岁人口比重低于江苏
C.徐州 60 岁以上人口比重高于全国
D.徐州 60 岁以上人口比重高于江苏
D
知2-练
如图 15.2-4 是一位发烧病人 4 月 7 日至 4 月 9 日体温变化的折线统计图,请根据折线统计图回答下列问题:
例4
知2-练
(1)护士每隔几小时给病人量一次体温?
(2)这位病人的最高体温是多少?最低体温是多少?
(3)这位病人在 4 月 8 日 12 时的体温是多少?
(4)从图中看,这位病人的病情是严重了还是好转了?
知2-练
解题秘方:紧扣折线统计图的特点,利用折线统计图中提供的信息解决问题 .
解:(1)护士每隔 6 小时给病人量一次体温 .
(2)这位病人的最高体温是 39.5℃,最低体温是 36.8℃ .
(3)这位病人在 4 月 8 日 12 时的体温是 37.5℃ .
(4)从图中看,这位病人的病情总体上是好转了 .
知2-练
4-1. [ 中考·株洲 ] 某月1 日 -10 日,甲、乙两人的手机“微信运动”的步数统计图如图所示,则下列错误的结论是( )
A.1 日 -10 日,甲的步数逐天增加
B.1 日 -6 日,乙的步数逐天减少
C.第 9 日,甲、乙两人的步数正好相等
D.第 11 日,甲的步数不一定比乙的步数多
B
知2-练
某校开展以“了解传统习俗,弘扬民族文化”为主题的实践活动 . 实践小组就“是否知道端午节的由来”这个问题,对部分学生进行了调查,调查结果如图15.2-5,其中“不知道”的学生有 8 人 .
例5
知2-练
下列说法不正确的是( )
A. 被调查的学生共有 50 人
B. 被调查的学生中“知道”的有 32 人
C. 图中“记不清”对应的扇形的圆心角为 60°
D. 全校“知道”的人数约占全校总人数的 64%
知2-练
解题秘方:根据“不知道”的学生的人数及其所占百分比求得总人数 . 根据已知部分求全体用除法,已知全体求部分用乘法进行分析求解 .
知2-练
答案:C
解:被调查的学生共有 8÷16%=50(人),故 A 正确;被
调查的学生中“知道”的有 50×64%=32(人),故 B 正确;“记不清”的学生人数所占的百分比是 1 - 16% - 64%=20%,则图中“记不清”对应的扇形的圆心角为 20%×360° =72°,故 C 错误;全校“知道”的人数约占全校总人数的 64%,故 D 正确 .
知2-练
5-1. [ 期末· 南阳 ] 如图是某种学生快餐(共400 g)营养成分扇形统计图,已知其中表示脂肪的扇形的圆心角为 36° ,维生素和矿物质含量占脂肪的一半,蛋白质含量比碳水化合物多 40 g.
知2-练
有关这份快餐,下列说法正确的是( )
A.表示维生素和矿物质 的扇形的圆心角为 20°
B.脂肪有 44 g,含量超过 10%
C.表示碳水化合物的扇形的圆心角为 135°
D.蛋白质的含量为维生 素和矿物质的 9 倍
C
知2-练
(1)我国五座名山的海拔高度如下表 . 若想根据表中的数据绘制统计图,以便更清楚地比较五座名山的高度,可选用( )
A. 条形统计图 B. 折线统计图 C. 扇形统计图
例6
山名 泰山 华山 衡山 恒山 嵩山
海拔 /m 1 532.7 2 154.9 1 300.2 2 016.1 1 491.7
知2-练
(2)某学校八(3)班的同学订阅了杂志(每人仅订一种),30% 的同学订阅了《科学画报》, 20% 的同学订阅了《作文通讯》, 40% 的同学订阅了《英语周刊》, 10% 的同学订阅了其他杂志,能表示上述数据的统计图是( )
A. 条形统计图 B. 折线统计图 C. 扇形统计图
知2-练
(3)某地上半年每月的平均气温依次是 5 ℃, 8 ℃, 12 ℃,18 ℃, 24 ℃, 30 ℃ . 为了表示出气温的变化情况,可以把上述数据绘制成( )
A. 条形统计图 B. 折线统计图 C. 扇形统计图
知2-练
答案:(1) A (2) C (3) B
解题秘方:根据三种统计图各自的特点和适用情况作出正确选择 .
解:(1)中要清楚地反映出五座名山的高度,宜选用条形统计图;(2)中已知的数据均为各部分占总体的百分比,因此应选用扇形统计图;(3)中要反映出气温的变化情况,折线统计图较为合适 .
知2-练
6-1.要表示一个家庭一年用于“教育”“服装”“食品”“其他”这四项的支出各占家庭本年总支出的百分比,从“扇形统计图”“条形统计图”“折线统计图”中选择一种统计图,最适合的统计图是 __________.
扇形统计图
数据的表示
工具
条形统计图
统计图
数据的
表示
扇形统计图
折线统计图
传递信息
逐点
导讲练
课堂小结
作业提升
课时讲解
1
课时流程
2
扇形统计图
利用统计图表传递信息
知1-讲
知识点
扇形统计图
1
1.扇形统计图 扇形统计图是用整个圆代表所研究的总体,用圆中各个扇形代表组成总体的各个部分 .
特别提醒: 扇形统计图中各部分在总体中所占百分比之和为 1(有时由于计算过程中四舍五入的原因,实际百分比之和并不刚好等于 1),与圆的大小无关 .
知1-讲
特别解读
1. 在同一个扇形统计图中,扇形圆心角的度数越大,相应的扇形面积也越大,该部分占总体的百分比也就越大;反之,则越小 .
2. 扇形统计图一般有两种形式:一种以百分比的形式出现;另一种以度数的形式出现 . 根据具体题目,可通过百分比求出相应部分的圆心角度数,同样也可根据圆心角度数求出相应的百分比 .
2. 优缺点 扇形统计图的优点是可以看出被统计对象所占总数量的百分比,缺点是不能从统计图中看出具体的数量 .
知1-讲
3. 制作扇形统计图的一般步骤
(1)计算出各部分在总体中所占的百分比;
(2)用 360°乘各部分在总体中所占的百分比,计算出各部分所对应的扇形圆心角的度数;
(3)以适当长为半径画圆,根据算出的各圆心角的度数画出各扇形;
(4)在每个扇形上注明相应的名称和百分比,各部分的名称可以注在图上,也可用图例标明 .
知1-讲
知1-练
[ 中考·达州 ]某校在今年“五· 四”开展了“好书伴我成长”的读书活动.为了解八年级 450 名学生的读书情况,随机调查了八年级 50 名学生本学期读书册数,并将统计数据制成了扇形统计图,如图 15.2-1,则该校八年级学生读书册数等于 3 册的约有_____ 名 .
例1
知1-练
解题秘方:紧扣扇形统计图中的基本特征,求出未知部分的百分比 . 再算出未知部分的数量 .
知1-练
解:由扇形统计图可知,随机调查的八年级 50 名学生中读书册数等于 3 册的学生人数所占的百分比为 1- 6% - 24% - 30% - 6%=34%,即 m%=34%,
所以该校八年级学生读书册数等于 3 册的约有 450×34%=153(名) .
答案:153
知1-练
1-1. [ 中考·温州 ] 某校参加课外兴趣小组的学生人数统计图如图所示 . 若信息技术小组有 60 人,则劳动实践小组有( )
A. 75 人 B. 90 人
C. 108 人 D. 150 人
B
知1-练
某校准备搬迁到新校舍,在迁入新校舍前,同学们就该校 300 名学生如何到校问题进行了一次调查,并得到下列数据:步行 60 人,骑自行车 100 人,坐公共汽车 130 人,其他 10 人,将上面的数据制成扇形统计图 .
例2
知1-练
解题秘方:紧扣绘制扇形统计图的步骤,先求出各部分所占的百分比,再计算各部分所对应扇形的圆心角的度数,最后绘制扇形统计图 .
知1-练
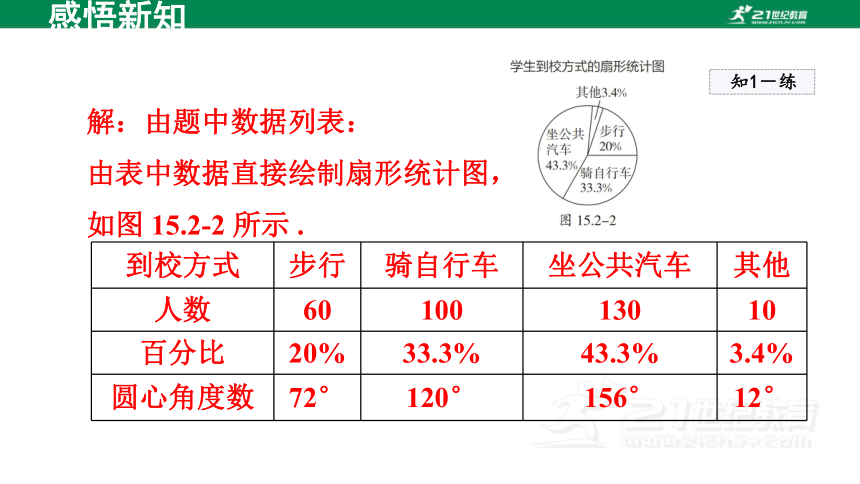
感悟新知
解:由题中数据列表:
由表中数据直接绘制扇形统计图,
如图 15.2-2 所示 .
到校方式 步行 骑自行车 坐公共汽车 其他
人数 60 100 130 10
百分比 20% 33.3% 43.3% 3.4%
圆心角度数 72° 120° 156° 12°
知1-练
2-1.下表是对某中学八(4)班的同学就“父母回家后,你会主动给他们倒一杯水吗”的调查结果 . 请你按要求用扇形统计图表示该调查的结果 .
项目 主动 倒水 偶尔 倒水 不倒水
人数 27 18 15
项目 主动 倒水 偶尔 倒水 不倒水
百分比
圆心角 度数
知1-练
(1)计算各部分人数所占百分比及扇形各个圆心角的度数,并填入下表:
45% 30% 25%
162° 108° 90°
知1-练
(2)制作扇形统计图,并标上百分比 .
解:对某中学八(4)班的同学就“父母回家后,你会主动给他们倒一杯水吗”的调查结果制作扇形统计图如图所示.
知2-讲
知识点
利用统计图表传递信息
2
数据的描述方法有统计表和统计图两种
(1) 统计表的作用:
①使数据更直观、清楚,便于分析;
②用数据把研究对象之间的变化规律清楚地表示出来;
③用数据把研究对象之间的差别清楚地表示出来,以便
于人们分析问题和研究问题 .
知2-讲
(2)统计图的作用:
统计图 条形统计图 折线统计图 扇形统计图
特点 用一个单位长度表示一定的数量,用直条的高低表示数量的多少 用一个单位长度表示一定的数量,用折线的起伏表示数 量的增减变化 用整个圆表示总体,用圆中各个扇形表 示总体的各个部分
知2-讲
图例
知2-讲
作用 能清楚地表示每个项目的具体数目,便于相互比较 能清楚地看出数量增减变化的情况,也能看出各数量的多少 能清楚地表示各部分在总体中所占的百分比
选用 表示数据的数量特征时 表示数据的发展变化趋势时 表示各部分数据占总体的百分比时
知2-讲
特别解读
1. 分析条形统计图、折线统计图时,首先要看统计图的横轴和纵轴分别代表什么量;分析扇形统计图时,根据各部分所占百分比或各部分所对应的扇形的圆心角度数来分析解答.
2. 绘制统计图时,根据绘图的一般步骤进行绘制 .
知2-练
高叔叔在池塘里养了许多鱼,各种鱼的数量如图15.2-3,下列说法正确的是( )
A. 草鱼的条数比鲢鱼多
B. 鲤鱼在所有鱼中所占比例最小
C. 鲢鱼在所有鱼中所占比例最大
D. 鲫鱼的条数最多
例3
知2-练
答案:D
解题秘方:紧扣条形统计图的特点,利用条形统计图提供的数据信息进行判断 .
解:由直条的高度可知鲫鱼条数最多,其次是鲢鱼、鲤鱼,草鱼最少,故草鱼的条数比鲢鱼少,选项 A 错误;在所有鱼中所占比例最小的是草鱼,所占比例最大的是鲫鱼,故选项 B、C 错误 .
知2-练
3-1. [ 中考·徐州 ] 第七次全国人口普查的部分结果如图所示 .根据该统计图,下列判断错误的是( )
A.徐州 0~14 岁人口比重高于全国
B.徐州 15~59 岁人口比重低于江苏
C.徐州 60 岁以上人口比重高于全国
D.徐州 60 岁以上人口比重高于江苏
D
知2-练
如图 15.2-4 是一位发烧病人 4 月 7 日至 4 月 9 日体温变化的折线统计图,请根据折线统计图回答下列问题:
例4
知2-练
(1)护士每隔几小时给病人量一次体温?
(2)这位病人的最高体温是多少?最低体温是多少?
(3)这位病人在 4 月 8 日 12 时的体温是多少?
(4)从图中看,这位病人的病情是严重了还是好转了?
知2-练
解题秘方:紧扣折线统计图的特点,利用折线统计图中提供的信息解决问题 .
解:(1)护士每隔 6 小时给病人量一次体温 .
(2)这位病人的最高体温是 39.5℃,最低体温是 36.8℃ .
(3)这位病人在 4 月 8 日 12 时的体温是 37.5℃ .
(4)从图中看,这位病人的病情总体上是好转了 .
知2-练
4-1. [ 中考·株洲 ] 某月1 日 -10 日,甲、乙两人的手机“微信运动”的步数统计图如图所示,则下列错误的结论是( )
A.1 日 -10 日,甲的步数逐天增加
B.1 日 -6 日,乙的步数逐天减少
C.第 9 日,甲、乙两人的步数正好相等
D.第 11 日,甲的步数不一定比乙的步数多
B
知2-练
某校开展以“了解传统习俗,弘扬民族文化”为主题的实践活动 . 实践小组就“是否知道端午节的由来”这个问题,对部分学生进行了调查,调查结果如图15.2-5,其中“不知道”的学生有 8 人 .
例5
知2-练
下列说法不正确的是( )
A. 被调查的学生共有 50 人
B. 被调查的学生中“知道”的有 32 人
C. 图中“记不清”对应的扇形的圆心角为 60°
D. 全校“知道”的人数约占全校总人数的 64%
知2-练
解题秘方:根据“不知道”的学生的人数及其所占百分比求得总人数 . 根据已知部分求全体用除法,已知全体求部分用乘法进行分析求解 .
知2-练
答案:C
解:被调查的学生共有 8÷16%=50(人),故 A 正确;被
调查的学生中“知道”的有 50×64%=32(人),故 B 正确;“记不清”的学生人数所占的百分比是 1 - 16% - 64%=20%,则图中“记不清”对应的扇形的圆心角为 20%×360° =72°,故 C 错误;全校“知道”的人数约占全校总人数的 64%,故 D 正确 .
知2-练
5-1. [ 期末· 南阳 ] 如图是某种学生快餐(共400 g)营养成分扇形统计图,已知其中表示脂肪的扇形的圆心角为 36° ,维生素和矿物质含量占脂肪的一半,蛋白质含量比碳水化合物多 40 g.
知2-练
有关这份快餐,下列说法正确的是( )
A.表示维生素和矿物质 的扇形的圆心角为 20°
B.脂肪有 44 g,含量超过 10%
C.表示碳水化合物的扇形的圆心角为 135°
D.蛋白质的含量为维生 素和矿物质的 9 倍
C
知2-练
(1)我国五座名山的海拔高度如下表 . 若想根据表中的数据绘制统计图,以便更清楚地比较五座名山的高度,可选用( )
A. 条形统计图 B. 折线统计图 C. 扇形统计图
例6
山名 泰山 华山 衡山 恒山 嵩山
海拔 /m 1 532.7 2 154.9 1 300.2 2 016.1 1 491.7
知2-练
(2)某学校八(3)班的同学订阅了杂志(每人仅订一种),30% 的同学订阅了《科学画报》, 20% 的同学订阅了《作文通讯》, 40% 的同学订阅了《英语周刊》, 10% 的同学订阅了其他杂志,能表示上述数据的统计图是( )
A. 条形统计图 B. 折线统计图 C. 扇形统计图
知2-练
(3)某地上半年每月的平均气温依次是 5 ℃, 8 ℃, 12 ℃,18 ℃, 24 ℃, 30 ℃ . 为了表示出气温的变化情况,可以把上述数据绘制成( )
A. 条形统计图 B. 折线统计图 C. 扇形统计图
知2-练
答案:(1) A (2) C (3) B
解题秘方:根据三种统计图各自的特点和适用情况作出正确选择 .
解:(1)中要清楚地反映出五座名山的高度,宜选用条形统计图;(2)中已知的数据均为各部分占总体的百分比,因此应选用扇形统计图;(3)中要反映出气温的变化情况,折线统计图较为合适 .
知2-练
6-1.要表示一个家庭一年用于“教育”“服装”“食品”“其他”这四项的支出各占家庭本年总支出的百分比,从“扇形统计图”“条形统计图”“折线统计图”中选择一种统计图,最适合的统计图是 __________.
扇形统计图
数据的表示
工具
条形统计图
统计图
数据的
表示
扇形统计图
折线统计图
传递信息
