12.3.2等腰三角形的判定(2) 课件(共19张PPT)
文档属性
| 名称 | 12.3.2等腰三角形的判定(2) 课件(共19张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 509.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-06 18:18:18 | ||
图片预览





文档简介
(共19张PPT)
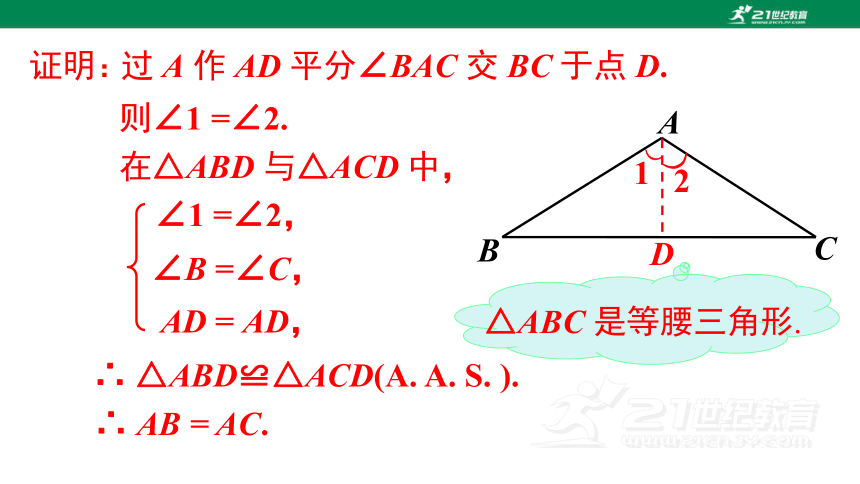
在△ABC 中,AB = AC,倘若不留神,它的一部分被墨水涂没了,只留下一条底边 BC 和一个底角∠C,请问,有没有办法把原来的等腰三角形画出来?
A
B
C
A
已知:如图,在△ABC 中,∠B =∠C,那么它们所对的边 AB 和 AC 有什么数量关系
建立数学模型:
C
A
B
做一做:画一个△ABC,其中∠B =∠C = 30°,请你量一量 AB与 AC 的长度,它们之间有什么数量关系?你能得出什么结论?
AB = AC
你能验证你的结论吗?
等腰三角形的判定
在△ABD 与△ACD 中,
∠1 =∠2,
∴ △ABD≌△ACD(A. A. S. ).
∠B =∠C,
AD = AD,
∴ AB = AC.
过 A 作 AD 平分∠BAC 交 BC 于点 D.
证明:
C
A
B
2
1
D
(
(
△ABC 是等腰三角形.
则∠1 =∠2.
∴ AC = AB ( ),
即△ABC 为等腰三角形.
∵∠B =∠C ( ),
知识要点
等腰三角形的判定方法
如果一个三角形有两个角相等,那么这个两个角所以的边也相等(简写成“等角对等边”).
已知
等角对等边
在△ABC 中,
应用格式:
B
C
A
(
(
等角对等边
等边对等角
例1 如图,在△ABC 中,已知∠A = 40°,∠B = 70°.求证:AB = AC.
A
B
C
证明:∵∠A + ∠B + ∠C = 180°,
∠A = 40°,∠B = 70°,
∴∠C = 180° -∠A -∠B,
= 180° - 40° - 70° = 70°.
∴∠C =∠B.
∴ AB = AC.
典例精析
例2 如图,AD∥BC,∠1 =∠2,求证:AB = AC.
A
B
C
E
(
(
1
2
D
证明:∵ AD∥BC (已知),
∴ ∠B =∠1 (两直线平行,同位角相等).
又∵ ∠1 =∠2,
∴ ∠B =∠2(等量代换).
∴ AC = BC(等角对等边).
一个三角形满足什么条件就是等边三角形?
由等腰三角形的判定定理,可得等边三角形的两个判定定理:
1. 三个角都相等的三角形是等边三角形;
2. 有一个角等于 60° 的等腰三角形是等边三角形.
你能证明这些定理吗?
等边三角形的判定
A
B
C
已知:如图,∠A =∠B =∠C.
求证: AB = AC = BC.
证明:∵ ∠A =∠B,
∴ AC = BC.
∵ ∠B =∠C,
∴ AB = AC.
∴ AB = AC = BC.
判定1:三个角都相等的三角形是等边三角形.
判定2:有一个角等于 60° 的等腰三角形是等边三角形.
证明:如图,在等腰三角形 ABC 中,AB = AC.
由三角形内角和定理得:∠A +∠B +∠C = 180°.
若顶角 ∠A = 60°,
则∠B +∠C = 180° - 60° = 120°.
又 AB = AC,
∴∠B =∠C.
∴∠B =∠C =∠A = 60°.
∴△ABC 是等边三角形.
如果是底角∠B = 60°
(或∠C = 60°) 呢?
例3 如图,在等边三角形 ABC 中,DE∥BC.
求证:△ADE 是等边三角形.
A
C
B
D
E
证明:
∵△ABC 是等边三角形,
∴∠A = ∠B = ∠C.
∵ DE∥BC,
∴∠ADE =∠B,∠AED =∠C.
∴∠A =∠ADE =∠AED .
∴△ADE 是等边三角形.
想一想:本题还有其他证法吗?
变式 上题中,若将条件 DE∥BC 改为 AD = AE,△ADE 还是等边三角形吗?试说明理由.
A
C
B
D
E
证明:
∵ △ABC 是等边三角形,
∴ ∠A = ∠B = ∠C = 60°.
∵ AD = AE,
∴ ∠ADE = ∠B,∠AED = ∠C.
∴ ∠A = ∠ADE = ∠AED = 60°.
∴ △ADE 是等边三角形.
例4 求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
已知:如图,∠CAE 是△ABC 的外角,∠1 =∠2,AD∥BC.
求证:AB = AC.
证明:∵AD∥BC,
∴∠1 =∠B (两直线平行,同位角相等),
∠2 =∠C (两直线平行,内错角相等).
又∵∠1 =∠2,∴∠B =∠C.
∴ AB = AC (等角对等边).
A
B
C
E
(
(
1
2
D
例5 如图,在 Rt△ABC 和 Rt△A'B'C' 中,
∠ACB =∠A'C'B' = 90°,AB = A'B',AC = A'C',
求证:Rt△ABC≌Rt△A'B'C'.
证明:由于直角边 AC = A'C',我们移动 Rt△ABC 使点 A 与点 A' 重合,点 C 和点 C' 重合,且使点 B 和点 B' 分别位于 A'C' 两侧.
A
C
B
B'
A'
C'
B
(A)
(C)
∵ ∠A'C'B =∠A'C'B' = 90° (已知),
∴ ∠B'C'B =∠A'C'B +∠A'C'B' = 180°.
即点 B、C'、B' 在同一条直线上.
在△A'B'B 中,∵AB = A'B' = A'B (已知),
∴ ∠B =∠B' (等边对等角).
在△ABC 和△A'B'C' 中,
∵∠B =∠B' (已证),
∠ACB =∠ A'C'B' (已知),
AC = A'C' (已知),
∴Rt△ABC≌Rt△A'B'C'(A. A. S. ).
B'
A'
A
C
B
C'
B
(A)
(C)
这样我们就证明了前面给出的 H. L. .判定定理
1. 在△ABC 中,已知∠A = 50°,∠B = 65°,判断△ABC 是什么三角形,为什么
△ABC是等腰三角形,因为∠B = 65°,∠A = 50°,所以∠C = 65°,∠B =∠C = 65°,所以△ABC 是等腰三角形.
2. 如图,已知∠A = 36°,∠DBC = 36°,∠C = 72°,则∠DBC = _____°,∠BDC = _____°,
图中的等腰三角形
有_______________________.
36
72
△ABC、
△DBA、
△BCD
A
B
C
D
3. 已知△ABC 中,∠A = ∠B = 60°,AB = 3 cm,则△ABC 的周长为______cm.
9
4.如图,等边三角形 ABC 的三条角平分线交于点 O,DE∥BC,则这个图形中的等腰三角形共有( )
A. 4 个 B. 5 个
C. 6 个 D. 7 个
D
A
C
B
D
E
O
5.如图,等边三角形 ABC 中,BD 是 AC 边上的中线,BD = BE,求∠EDA 的度数.
解:∵ △ABC 是等边三角形,
∴∠CBA = 60°.
∵BD 是 AC 边上的中线,
∴∠BDA = 90°,∠DBA = 30°.
∵ BD = BE,
∴ ∠BDE = (180° -∠DBA)÷2 =(180° - 30°)÷2 = 75°.
∴ ∠EDA = 90° -∠BDE = 90° - 75° = 15°.
B
C
D
A
E
解:∵△OAB 和△OCD 是两个全等的等边三角形,
∴AO = BO,CO = DO,∠AOB =∠COD = 60°.
∵ A,O,D 三点共线,
∴ ∠DOB =∠COA = 120°.
∴ △COA≌△DOB (S. A. S. ).
∴ ∠DBO =∠CAO.
设 OB 与 EA 相交于点 F,
∵ ∠EFB =∠AFO,∴ ∠AEB =∠AOB = 60°.
6.如图,A,O,D 三点共线,△OAB 和△OCD 是两个全等的等边三角形,求∠AEB 的大小.
C
B
O
D
A
E
F
等腰三角形
等腰三角形的判定:等角对等边.
等边三角形的判定:三个角都相等的三角形是等边三角形;有一个角是 60° 的等腰三角形是等边三角形.
在△ABC 中,AB = AC,倘若不留神,它的一部分被墨水涂没了,只留下一条底边 BC 和一个底角∠C,请问,有没有办法把原来的等腰三角形画出来?
A
B
C
A
已知:如图,在△ABC 中,∠B =∠C,那么它们所对的边 AB 和 AC 有什么数量关系
建立数学模型:
C
A
B
做一做:画一个△ABC,其中∠B =∠C = 30°,请你量一量 AB与 AC 的长度,它们之间有什么数量关系?你能得出什么结论?
AB = AC
你能验证你的结论吗?
等腰三角形的判定
在△ABD 与△ACD 中,
∠1 =∠2,
∴ △ABD≌△ACD(A. A. S. ).
∠B =∠C,
AD = AD,
∴ AB = AC.
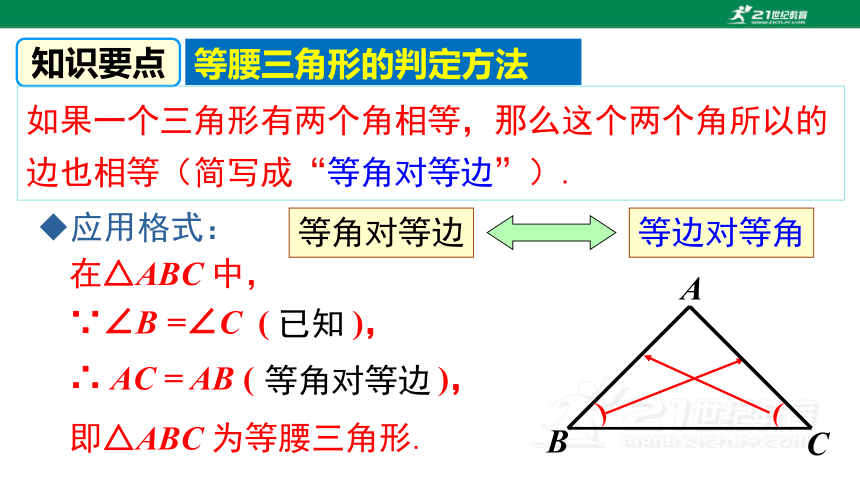
过 A 作 AD 平分∠BAC 交 BC 于点 D.
证明:
C
A
B
2
1
D
(
(
△ABC 是等腰三角形.
则∠1 =∠2.
∴ AC = AB ( ),
即△ABC 为等腰三角形.
∵∠B =∠C ( ),
知识要点
等腰三角形的判定方法
如果一个三角形有两个角相等,那么这个两个角所以的边也相等(简写成“等角对等边”).
已知
等角对等边
在△ABC 中,
应用格式:
B
C
A
(
(
等角对等边
等边对等角
例1 如图,在△ABC 中,已知∠A = 40°,∠B = 70°.求证:AB = AC.
A
B
C
证明:∵∠A + ∠B + ∠C = 180°,
∠A = 40°,∠B = 70°,
∴∠C = 180° -∠A -∠B,
= 180° - 40° - 70° = 70°.
∴∠C =∠B.
∴ AB = AC.
典例精析
例2 如图,AD∥BC,∠1 =∠2,求证:AB = AC.
A
B
C
E
(
(
1
2
D
证明:∵ AD∥BC (已知),
∴ ∠B =∠1 (两直线平行,同位角相等).
又∵ ∠1 =∠2,
∴ ∠B =∠2(等量代换).
∴ AC = BC(等角对等边).
一个三角形满足什么条件就是等边三角形?
由等腰三角形的判定定理,可得等边三角形的两个判定定理:
1. 三个角都相等的三角形是等边三角形;
2. 有一个角等于 60° 的等腰三角形是等边三角形.
你能证明这些定理吗?
等边三角形的判定
A
B
C
已知:如图,∠A =∠B =∠C.
求证: AB = AC = BC.
证明:∵ ∠A =∠B,
∴ AC = BC.
∵ ∠B =∠C,
∴ AB = AC.
∴ AB = AC = BC.
判定1:三个角都相等的三角形是等边三角形.
判定2:有一个角等于 60° 的等腰三角形是等边三角形.
证明:如图,在等腰三角形 ABC 中,AB = AC.
由三角形内角和定理得:∠A +∠B +∠C = 180°.
若顶角 ∠A = 60°,
则∠B +∠C = 180° - 60° = 120°.
又 AB = AC,
∴∠B =∠C.
∴∠B =∠C =∠A = 60°.
∴△ABC 是等边三角形.
如果是底角∠B = 60°
(或∠C = 60°) 呢?
例3 如图,在等边三角形 ABC 中,DE∥BC.
求证:△ADE 是等边三角形.
A
C
B
D
E
证明:
∵△ABC 是等边三角形,
∴∠A = ∠B = ∠C.
∵ DE∥BC,
∴∠ADE =∠B,∠AED =∠C.
∴∠A =∠ADE =∠AED .
∴△ADE 是等边三角形.
想一想:本题还有其他证法吗?
变式 上题中,若将条件 DE∥BC 改为 AD = AE,△ADE 还是等边三角形吗?试说明理由.
A
C
B
D
E
证明:
∵ △ABC 是等边三角形,
∴ ∠A = ∠B = ∠C = 60°.
∵ AD = AE,
∴ ∠ADE = ∠B,∠AED = ∠C.
∴ ∠A = ∠ADE = ∠AED = 60°.
∴ △ADE 是等边三角形.
例4 求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
已知:如图,∠CAE 是△ABC 的外角,∠1 =∠2,AD∥BC.
求证:AB = AC.
证明:∵AD∥BC,
∴∠1 =∠B (两直线平行,同位角相等),
∠2 =∠C (两直线平行,内错角相等).
又∵∠1 =∠2,∴∠B =∠C.
∴ AB = AC (等角对等边).
A
B
C
E
(
(
1
2
D
例5 如图,在 Rt△ABC 和 Rt△A'B'C' 中,
∠ACB =∠A'C'B' = 90°,AB = A'B',AC = A'C',
求证:Rt△ABC≌Rt△A'B'C'.
证明:由于直角边 AC = A'C',我们移动 Rt△ABC 使点 A 与点 A' 重合,点 C 和点 C' 重合,且使点 B 和点 B' 分别位于 A'C' 两侧.
A
C
B
B'
A'
C'
B
(A)
(C)
∵ ∠A'C'B =∠A'C'B' = 90° (已知),
∴ ∠B'C'B =∠A'C'B +∠A'C'B' = 180°.
即点 B、C'、B' 在同一条直线上.
在△A'B'B 中,∵AB = A'B' = A'B (已知),
∴ ∠B =∠B' (等边对等角).
在△ABC 和△A'B'C' 中,
∵∠B =∠B' (已证),
∠ACB =∠ A'C'B' (已知),
AC = A'C' (已知),
∴Rt△ABC≌Rt△A'B'C'(A. A. S. ).
B'
A'
A
C
B
C'
B
(A)
(C)
这样我们就证明了前面给出的 H. L. .判定定理
1. 在△ABC 中,已知∠A = 50°,∠B = 65°,判断△ABC 是什么三角形,为什么
△ABC是等腰三角形,因为∠B = 65°,∠A = 50°,所以∠C = 65°,∠B =∠C = 65°,所以△ABC 是等腰三角形.
2. 如图,已知∠A = 36°,∠DBC = 36°,∠C = 72°,则∠DBC = _____°,∠BDC = _____°,
图中的等腰三角形
有_______________________.
36
72
△ABC、
△DBA、
△BCD
A
B
C
D
3. 已知△ABC 中,∠A = ∠B = 60°,AB = 3 cm,则△ABC 的周长为______cm.
9
4.如图,等边三角形 ABC 的三条角平分线交于点 O,DE∥BC,则这个图形中的等腰三角形共有( )
A. 4 个 B. 5 个
C. 6 个 D. 7 个
D
A
C
B
D
E
O
5.如图,等边三角形 ABC 中,BD 是 AC 边上的中线,BD = BE,求∠EDA 的度数.
解:∵ △ABC 是等边三角形,
∴∠CBA = 60°.
∵BD 是 AC 边上的中线,
∴∠BDA = 90°,∠DBA = 30°.
∵ BD = BE,
∴ ∠BDE = (180° -∠DBA)÷2 =(180° - 30°)÷2 = 75°.
∴ ∠EDA = 90° -∠BDE = 90° - 75° = 15°.
B
C
D
A
E
解:∵△OAB 和△OCD 是两个全等的等边三角形,
∴AO = BO,CO = DO,∠AOB =∠COD = 60°.
∵ A,O,D 三点共线,
∴ ∠DOB =∠COA = 120°.
∴ △COA≌△DOB (S. A. S. ).
∴ ∠DBO =∠CAO.
设 OB 与 EA 相交于点 F,
∵ ∠EFB =∠AFO,∴ ∠AEB =∠AOB = 60°.
6.如图,A,O,D 三点共线,△OAB 和△OCD 是两个全等的等边三角形,求∠AEB 的大小.
C
B
O
D
A
E
F
等腰三角形
等腰三角形的判定:等角对等边.
等边三角形的判定:三个角都相等的三角形是等边三角形;有一个角是 60° 的等腰三角形是等边三角形.
