12.1.1命题 课件(共13张PPT)
文档属性
| 名称 | 12.1.1命题 课件(共13张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 342.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-06 18:19:05 | ||
图片预览





文档简介
(共13张PPT)
我们已经学过一些图形的特性,试判断下列句子是否正确?它们有什么共同点?
(1)三角形的内角和等于 180°;
(2)如果两个角是对顶角,那么这两个角相等;
(3)两直线平行,同旁内角相等;
(4)直角都相等;
(5)经过一点确定一条直线.
依据所学知识可以判断(1)(2)(4)是正确的,(3)(5)是错误的,这几个句子的特点是可以判断一件事情的正确或错误.
概念:它们都是判断某一件事情的语句,像这样表示判断的语句叫做命题.
例1 判断下列语句是不是命题?
(1) 长度相等的两条线段是相等的线段吗
(2) 两条直线相交,有且只有一个交点;
(3) 不相等的两个角不是对顶角;
(4) 欢迎前来参观! (5) 两个锐角的和是钝角;
(6) 取线段 AB 的中点 C.
注意:祈使句、疑问句、感叹句都不是命题
像 (1)、(4)、(6) 这样对某一件事的对错没有给出任何判断就不是命题.
命题
试 一 试
1. 你能举出一些命题吗?
2. 能否举出一些不是命题的语句?
观察下列命题,你能发现这些命题有什么共同的结构特征?与同学交流.
(1) 如果两个三角形的三条边相等,那么这两个三角形 全等;
(2) 如果一个三角形是等腰三角形,那么这个三角形的两个底角相等;
(3) 如果两个角是对顶角,那么这两个角相等.
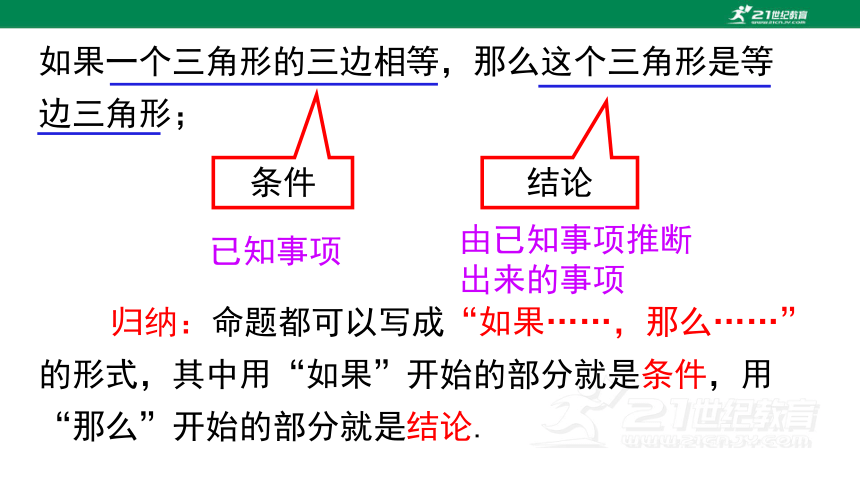
如果一个三角形的三边相等,那么这个三角形是等边三角形;
归纳:命题都可以写成“如果……,那么……”的形式,其中用“如果”开始的部分就是条件,用“那么”开始的部分就是结论.
条件
结论
已知事项
由已知事项推断
出来的事项
例1 指出下列命题的条件和结论,并改写成“如果……,那么……”的形式:
(1) 同位角相等,两直线平行;
(2) 三个角都相等的三角形是等边三角形.
条件:同位角相等
结论:两直线平行
改写成:如果一个三角形的三个角相等,
那么这个三角形是等边三角形.
结论:这个三角形是等边三角形
条件:一个三角形的三个角相等
改写成:两条直线被第三条直线所截,如果同位角相等,那么两直线平行.
典例精析
解析:其中 (1)(2)(4)是正确的,如果条件成立,那么结论一定成立. 像这样的命题,称为真命题. (3)(5)是错误的,当条件成立时,不能保证结论总是正确,也就是说结论不成立. 像这样的命题,称为假命题.
(1) 三角形的内角和等于 180°;
(2) 如果两个角是对顶角,那么这两个角相等;
(3) 两直线平行,同旁内角相等;
(4) 直角都相等;
(5) 经过一点确定一条直线.
判断下列命题是否正确?
真命题与假命题
例2 哪些是真命题,哪些是假命题?
(1)一个角的补角大于这个角;
(2)相等的两个角是对顶角;
(3)两点可以确定一条直线;
(4)若 A = B,则 2A = 2B;
(5)锐角和钝角互为补角;
(6)两点之间线段最短.
(假命题)
(假命题)
(真命题)
(真命题)
(假命题)
(真命题)
1. 要判断一个命题是真命题,可以用演绎推理加以论证;
2. 要判断一个命题是假命题,只要举出一个例子,说明该命题不成立,比如(1)中若∠A = 120°,那么它的补角是 60°,从而它的补角比∠A 小,所以(1)是假命题. 在数学中,这种方法称为“举反例”.
1. 下列句子中,哪些是命题?哪些不是命题?
(1)对顶角相等;
(2)画一个角等于已知角;
(3)两直线平行,同位角相等;
(4)a,b 两条直线平行吗?
(5)温柔的李明明;
(6)玫瑰花是动物;
(7)若 a2=4,求 a 的值;
(8)若 a2= b2,则 a=b.
不是
是
不是
是
是
不是
是
不是
2.把下列命题改写成“如果……,那么……”的形式,并分别指出它们的条件和结论:
(1) 全等三角形的对应边相等;
解:(1) 改写成:如果两个三角形全等,那么它们的对应边相等.
条件:两个三角形全等;
结论:这两个三角形的对应边相等.
(2) 在同一平面内,垂直于同一条直线的两条直线互相平行.
(2) 改写成:如果在同一平面内,有两条直线分别垂直于第三条直线,那么这两条直线互相平行.
条件:在同一平面内,有两条直线分别垂直于第三条直线;
结论:这两条直线互相平行.
3. 指出下列命题中的真命题和假命题:
(1)同位角相等,两直线平行;
(2)多边形的内角和等于 180°;
(3)三角形的外角和等于 360°;
(4)平行于同一条直线的两条直线互相平行.
(真命题)
(假命题)
(真命题)
(真命题)
命 题
命题的概念:表示判断的语句叫做命题
命题的结构:由条件和结论两部分组成,常写成“如果……,那么……”的形式
命题的分类:真命题和假命题
我们已经学过一些图形的特性,试判断下列句子是否正确?它们有什么共同点?
(1)三角形的内角和等于 180°;
(2)如果两个角是对顶角,那么这两个角相等;
(3)两直线平行,同旁内角相等;
(4)直角都相等;
(5)经过一点确定一条直线.
依据所学知识可以判断(1)(2)(4)是正确的,(3)(5)是错误的,这几个句子的特点是可以判断一件事情的正确或错误.
概念:它们都是判断某一件事情的语句,像这样表示判断的语句叫做命题.
例1 判断下列语句是不是命题?
(1) 长度相等的两条线段是相等的线段吗
(2) 两条直线相交,有且只有一个交点;
(3) 不相等的两个角不是对顶角;
(4) 欢迎前来参观! (5) 两个锐角的和是钝角;
(6) 取线段 AB 的中点 C.
注意:祈使句、疑问句、感叹句都不是命题
像 (1)、(4)、(6) 这样对某一件事的对错没有给出任何判断就不是命题.
命题
试 一 试
1. 你能举出一些命题吗?
2. 能否举出一些不是命题的语句?
观察下列命题,你能发现这些命题有什么共同的结构特征?与同学交流.
(1) 如果两个三角形的三条边相等,那么这两个三角形 全等;
(2) 如果一个三角形是等腰三角形,那么这个三角形的两个底角相等;
(3) 如果两个角是对顶角,那么这两个角相等.
如果一个三角形的三边相等,那么这个三角形是等边三角形;
归纳:命题都可以写成“如果……,那么……”的形式,其中用“如果”开始的部分就是条件,用“那么”开始的部分就是结论.
条件
结论
已知事项
由已知事项推断
出来的事项
例1 指出下列命题的条件和结论,并改写成“如果……,那么……”的形式:
(1) 同位角相等,两直线平行;
(2) 三个角都相等的三角形是等边三角形.
条件:同位角相等
结论:两直线平行
改写成:如果一个三角形的三个角相等,
那么这个三角形是等边三角形.
结论:这个三角形是等边三角形
条件:一个三角形的三个角相等
改写成:两条直线被第三条直线所截,如果同位角相等,那么两直线平行.
典例精析
解析:其中 (1)(2)(4)是正确的,如果条件成立,那么结论一定成立. 像这样的命题,称为真命题. (3)(5)是错误的,当条件成立时,不能保证结论总是正确,也就是说结论不成立. 像这样的命题,称为假命题.
(1) 三角形的内角和等于 180°;
(2) 如果两个角是对顶角,那么这两个角相等;
(3) 两直线平行,同旁内角相等;
(4) 直角都相等;
(5) 经过一点确定一条直线.
判断下列命题是否正确?
真命题与假命题
例2 哪些是真命题,哪些是假命题?
(1)一个角的补角大于这个角;
(2)相等的两个角是对顶角;
(3)两点可以确定一条直线;
(4)若 A = B,则 2A = 2B;
(5)锐角和钝角互为补角;
(6)两点之间线段最短.
(假命题)
(假命题)
(真命题)
(真命题)
(假命题)
(真命题)
1. 要判断一个命题是真命题,可以用演绎推理加以论证;
2. 要判断一个命题是假命题,只要举出一个例子,说明该命题不成立,比如(1)中若∠A = 120°,那么它的补角是 60°,从而它的补角比∠A 小,所以(1)是假命题. 在数学中,这种方法称为“举反例”.
1. 下列句子中,哪些是命题?哪些不是命题?
(1)对顶角相等;
(2)画一个角等于已知角;
(3)两直线平行,同位角相等;
(4)a,b 两条直线平行吗?
(5)温柔的李明明;
(6)玫瑰花是动物;
(7)若 a2=4,求 a 的值;
(8)若 a2= b2,则 a=b.
不是
是
不是
是
是
不是
是
不是
2.把下列命题改写成“如果……,那么……”的形式,并分别指出它们的条件和结论:
(1) 全等三角形的对应边相等;
解:(1) 改写成:如果两个三角形全等,那么它们的对应边相等.
条件:两个三角形全等;
结论:这两个三角形的对应边相等.
(2) 在同一平面内,垂直于同一条直线的两条直线互相平行.
(2) 改写成:如果在同一平面内,有两条直线分别垂直于第三条直线,那么这两条直线互相平行.
条件:在同一平面内,有两条直线分别垂直于第三条直线;
结论:这两条直线互相平行.
3. 指出下列命题中的真命题和假命题:
(1)同位角相等,两直线平行;
(2)多边形的内角和等于 180°;
(3)三角形的外角和等于 360°;
(4)平行于同一条直线的两条直线互相平行.
(真命题)
(假命题)
(真命题)
(真命题)
命 题
命题的概念:表示判断的语句叫做命题
命题的结构:由条件和结论两部分组成,常写成“如果……,那么……”的形式
命题的分类:真命题和假命题
