12.3.1等腰三角形的性质(1) 课件(共45张PPT)
文档属性
| 名称 | 12.3.1等腰三角形的性质(1) 课件(共45张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-06 18:22:33 | ||
图片预览










文档简介
(共45张PPT)
逐点
导讲练
课堂小结
作业提升
课时讲解
1
课时流程
2
等腰三角形的定义
等腰三角形的性质
等边三角形的定义及性质
知1-讲
知识点
等腰三角形的定义
1
1.定义 有两条边相等的三角形叫做等腰三角形 .
几何语言: 如图 13.3-1,在△ ABC 中,
∵ AB=AC,∴△ ABC 为等腰三角形 .
知1-讲
特别解读
1. 确定等腰三角形的两条腰时,应找三角形中相等的两边,腰与三角形本身的位置无关.
2. 等腰三角形的顶角可以是锐角、直角或钝角,但底角只能是锐角 .
2. 相关概念 等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角 .
知1-讲
知1-练
若某个等腰三角形的两边长分别为 4 和 6,求这个等腰三角形的周长 .
例1
知1-练
解题秘方:根据等腰三角形的定义确定腰和底边的长,再利用三角形三边关系进行判断并计算 .
知1-练
解: ∵等腰三角形的底边长和腰长不确定,
∴需分两种情况讨论 .
第一种情况:当 4 为腰长时,该等腰三角形的三边长分别为 4、 4、 6,
∵ 4+4>6,满足三角形的三边关系,
∴周长 =4+4+6=14;
知1-练
第二种情况:当 6 为腰长时,该等腰三角形的三边长分别为 4、 6、 6,
∵ 4+6>6,满足三角形的三边关系,
∴周长 =6+6+4=16.
综上可知,这个等腰三角形的周长为 14 或 16.
知1-练
特别提醒 :等腰三角形的边分腰和底边,若没有说明,则必须分类讨论,同时注意三角形的三边关系 .
知1-练
1-1.已知等腰三角形的一边长为 5,周长为20,则该等腰三角形的腰长为 ___________.
7.5
知1-练
1-2.已知三角形的三边长 a、 b、 c 满足( a-b) ·( b - c ) ( a - c ) =0,则三角形的形状是___________ .
等腰三角形
知2-讲
知识点
等腰三角形的性质
2
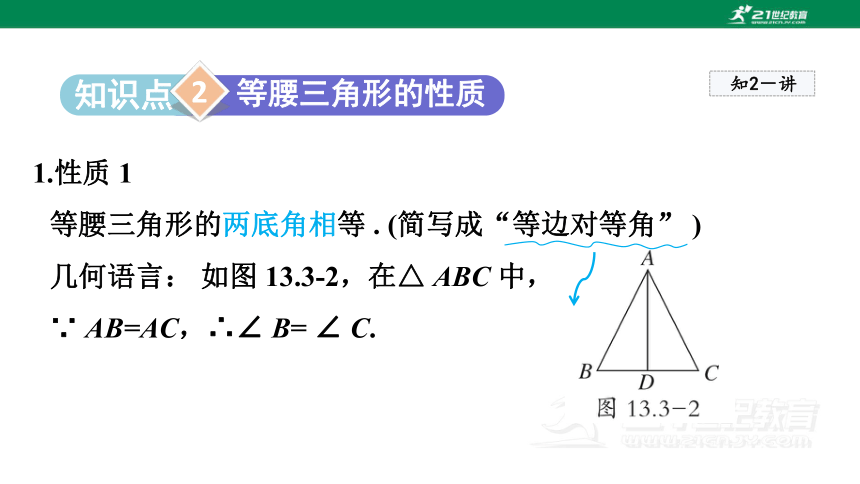
1.性质 1
等腰三角形的两底角相等 . (简写成“等边对等角” )
几何语言: 如图 13.3-2,在△ ABC 中,
∵ AB=AC,∴∠ B= ∠ C.
知2-讲
特别提醒
●适用条件:必须在同一个三角形中 .
●“等边对等角”是证明角相等的常用方法,应用它证角相等时可省去三角形全等的证明,因而更简便.
知2-讲
2. 性质 2 等腰三角形底边上的高、中线及顶角的平分线互相重合 . (简称“三线合一” )
几何语言: 如图 13.3-2,在△ ABC 中,
(1)∵ AB=AC, AD ⊥ BC 于 D,
∴ AD 平分∠ BAC(或 BD=CD);
知2-讲
特别解读
●适用条件:
1.必须是等腰三角形;
2. 必须是底边上的中线、底边上的高和顶角的平分线才互相重合 .
●作用:是证明线段相等、角相等、线段垂直的重要依据 .
知2-讲
(2)∵ AB=AC, BD=DC,
∴ AD ⊥ BC(或 AD 平分∠ BAC);
(3)∵ AB=AC, AD 平分∠ BAC,
∴ BD=DC(或 AD ⊥ BC).
知2-讲
3. 对称性 等腰三角形是轴对称图形,顶角平分线(或底边上的高、底边上的中线)所在的直线是它的对称轴.
知2-练
如图 13.3-3,在△ ABC 中, AB=AC, AD 平分∠ BAC.
(1)求∠ ADB 的度数;
(2)若∠ BAC=100°,求∠ B、∠ C 的度数;
(3)若 BC=3 cm,求 BD 的长 .
例2
知2-练
解题秘方:紧扣等腰三角形的性质进行解答 .
解:(1)∵ AB=AC, AD 平分∠ BAC,
∴ AD ⊥ BC. ∴∠ ADB=90° .
知2-练
知2-练
2-1. [ 中考· 淄博 ] 某城市几条道路的位置关系如图所示, 道路 AB ∥ CD, 道路 AB与 AE 的夹角∠ BAE =50°.城市规划部门想新修一条道路 CE,要求CF = EF,则∠ E 的度数为( )
A. 23° B. 25°
C. 27° D. 30°
B
知2-练
如图 13.3-4,已知 AB=AC, AD=AE.
求证: BD=CE.
例3
知2-练
解题秘方:证明线段相等,可证明其所在的三角形全等;条件中出现两个等腰三角形,也可利用等腰三角形的性质证明 .
知2-练
证明: 方法一 ∵ AB=AC , AD=AE,
∴∠ B= ∠ C,∠ ADE= ∠ AED. ∴∠ BAD= ∠ CAE.
∴△ ABD ≌△ ACE ( A.S.A. ) . ∴ BD=CE.
方法二 如图 13.3-4,过点 A 作 AF ⊥ DE,垂足为 F.
∵ AD=AE,∴ DF=EF.
又∵ AB=AC,∴ BF=CF.
∴ BF - DF=CF - EF,即 BD=CE.
知2-练
3-1. [ 中考· 淄博 ] 如图,△ ABC 是等腰三角形, 点 D, E 分别在腰AC, AB 上, 且 BE =CD,连结 BD, CE.求证: BD = CE.
知2-练
知3-讲
知识点
等边三角形的定义及性质
3
1.定义 三条边都相等的三角形是等边三角形 .
知3-讲
2. 性质 (1)等边三角形的三条边都相等 .
(2)等边三角形的各个角都相等,并且每一个角都等于 60° .
(3)等边三角形是轴对称图形,它有 3 条对称轴,分别为三边的垂直平分线 .
(4)各边上的高、中线、对应的角平分线重合,且长度相等 .
知3-讲
特别解读
等边三角形是特殊的等腰三角形,具备等腰三角形的所有性质:
任意两边都可以作为腰;
任意一个角都可以作为顶角 .
知3-练
如图 13.3-5,△ ABC 是等边三角形, D、 E、 F 分别是三边 AB、 AC、 BC 上 的 点, 且 DE ⊥ AC, EF ⊥ BC,DF ⊥ AB,请计算△ DEF 各个内角的度数 .
例4
知3-练
解题秘方:紧扣等边三角形的三个内角都等于 60° 求解 .
知3-练
解:∵△ ABC 是等边三角形,
∴∠ A= ∠ B= ∠ C=60° .
∵ DE ⊥ AC, EF ⊥ BC, DF ⊥ AB,
∴∠ AED= ∠ EFC= ∠ FDB=90° .
∴∠ ADE=90°-∠ A=90°-60° =30° .
∴∠ EDF=180° -30°-90° =60°,
同理可得∠ DEF= ∠ EFD=60°,
∴△ DEF 各个内角的度数都是 60° .
知3-练
4-1. [ 中考· 鞍山 ] 如图, 直线 a ∥ b, 等边三角形 ABC 的顶点 C 在直线 b 上,∠ 2=40° ,则∠ 1 的度数为( )
A.80° B.70°
C.60° D.50°
A
知3-练
如图 13.3-6,等边三角形 ABC 的边长为 3, D 是 AC的中点,点 E 在 BC 的延长线上 . 若 DE=DB,求 CE 的长 .
例5
知3-练
解题秘方:利用等边三角形“三线合一”的性质将未知线段向已知线段转化 .
知3-练
知3-练
知3-练
5-1.如图,△ ABC 为等边三角形, AD ⊥ BC, AE=AD,则∠ ADE=_________ ° .
75
知3-练
如图 13.3-7,已知△ ABC 为等边三角形,点 D、 E分别在 BC、 AC 边上,且 AE=CD, AD 与 BE 相交于点 F.
例6
知3-练
解题秘方:利用等边三角形中边相等、角相等且为 60°的性质进行解答 .
知3-练
(1)求证:△ ABE ≌△ CAD;
知3-练
解: ∵△ ABE ≌△ CAD,
∴∠ ABE= ∠ CAD.
∵∠ BFD= ∠ ABE+ ∠ BAF,
∴∠ BFD= ∠ DAC+ ∠ BAF= ∠ BAC=60° .
(2)求∠ BFD 的度数 .
知3-练
6-1.如图, △ ABC 为等边三角形, D 为边BA 延长线上一点, 连结 CD, 以 CD 为 边 作等边三角形 CDE,连结AE, 判断 AE 与 BC 的位置关系,并说明理由 .
知5-练
解:AE∥BC.理由如下:
∵△ABC与△CDE都为等边三角形,
∴BC=AC,CD=CE,∠B=∠ACB=∠DCE=60°.
∴∠ACB+∠ACD=∠DCE+∠ACD,
即∠BCD=∠ACE.
∴△BCD≌△ACE(S.A.S.).∴∠B=∠EAC.
又∵∠B=∠ACB,∴∠EAC=∠ACB.∴AE∥BC.
等腰三角形的性质
特殊
两边相等
等腰
三角形
等边三角形
三线合一
性质
特性
三边相等,三个内角相等
等边对等角
都具有
逐点
导讲练
课堂小结
作业提升
课时讲解
1
课时流程
2
等腰三角形的定义
等腰三角形的性质
等边三角形的定义及性质
知1-讲
知识点
等腰三角形的定义
1
1.定义 有两条边相等的三角形叫做等腰三角形 .
几何语言: 如图 13.3-1,在△ ABC 中,
∵ AB=AC,∴△ ABC 为等腰三角形 .
知1-讲
特别解读
1. 确定等腰三角形的两条腰时,应找三角形中相等的两边,腰与三角形本身的位置无关.
2. 等腰三角形的顶角可以是锐角、直角或钝角,但底角只能是锐角 .
2. 相关概念 等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角 .
知1-讲
知1-练
若某个等腰三角形的两边长分别为 4 和 6,求这个等腰三角形的周长 .
例1
知1-练
解题秘方:根据等腰三角形的定义确定腰和底边的长,再利用三角形三边关系进行判断并计算 .
知1-练
解: ∵等腰三角形的底边长和腰长不确定,
∴需分两种情况讨论 .
第一种情况:当 4 为腰长时,该等腰三角形的三边长分别为 4、 4、 6,
∵ 4+4>6,满足三角形的三边关系,
∴周长 =4+4+6=14;
知1-练
第二种情况:当 6 为腰长时,该等腰三角形的三边长分别为 4、 6、 6,
∵ 4+6>6,满足三角形的三边关系,
∴周长 =6+6+4=16.
综上可知,这个等腰三角形的周长为 14 或 16.
知1-练
特别提醒 :等腰三角形的边分腰和底边,若没有说明,则必须分类讨论,同时注意三角形的三边关系 .
知1-练
1-1.已知等腰三角形的一边长为 5,周长为20,则该等腰三角形的腰长为 ___________.
7.5
知1-练
1-2.已知三角形的三边长 a、 b、 c 满足( a-b) ·( b - c ) ( a - c ) =0,则三角形的形状是___________ .
等腰三角形
知2-讲
知识点
等腰三角形的性质
2
1.性质 1
等腰三角形的两底角相等 . (简写成“等边对等角” )
几何语言: 如图 13.3-2,在△ ABC 中,
∵ AB=AC,∴∠ B= ∠ C.
知2-讲
特别提醒
●适用条件:必须在同一个三角形中 .
●“等边对等角”是证明角相等的常用方法,应用它证角相等时可省去三角形全等的证明,因而更简便.
知2-讲
2. 性质 2 等腰三角形底边上的高、中线及顶角的平分线互相重合 . (简称“三线合一” )
几何语言: 如图 13.3-2,在△ ABC 中,
(1)∵ AB=AC, AD ⊥ BC 于 D,
∴ AD 平分∠ BAC(或 BD=CD);
知2-讲
特别解读
●适用条件:
1.必须是等腰三角形;
2. 必须是底边上的中线、底边上的高和顶角的平分线才互相重合 .
●作用:是证明线段相等、角相等、线段垂直的重要依据 .
知2-讲
(2)∵ AB=AC, BD=DC,
∴ AD ⊥ BC(或 AD 平分∠ BAC);
(3)∵ AB=AC, AD 平分∠ BAC,
∴ BD=DC(或 AD ⊥ BC).
知2-讲
3. 对称性 等腰三角形是轴对称图形,顶角平分线(或底边上的高、底边上的中线)所在的直线是它的对称轴.
知2-练
如图 13.3-3,在△ ABC 中, AB=AC, AD 平分∠ BAC.
(1)求∠ ADB 的度数;
(2)若∠ BAC=100°,求∠ B、∠ C 的度数;
(3)若 BC=3 cm,求 BD 的长 .
例2
知2-练
解题秘方:紧扣等腰三角形的性质进行解答 .
解:(1)∵ AB=AC, AD 平分∠ BAC,
∴ AD ⊥ BC. ∴∠ ADB=90° .
知2-练
知2-练
2-1. [ 中考· 淄博 ] 某城市几条道路的位置关系如图所示, 道路 AB ∥ CD, 道路 AB与 AE 的夹角∠ BAE =50°.城市规划部门想新修一条道路 CE,要求CF = EF,则∠ E 的度数为( )
A. 23° B. 25°
C. 27° D. 30°
B
知2-练
如图 13.3-4,已知 AB=AC, AD=AE.
求证: BD=CE.
例3
知2-练
解题秘方:证明线段相等,可证明其所在的三角形全等;条件中出现两个等腰三角形,也可利用等腰三角形的性质证明 .
知2-练
证明: 方法一 ∵ AB=AC , AD=AE,
∴∠ B= ∠ C,∠ ADE= ∠ AED. ∴∠ BAD= ∠ CAE.
∴△ ABD ≌△ ACE ( A.S.A. ) . ∴ BD=CE.
方法二 如图 13.3-4,过点 A 作 AF ⊥ DE,垂足为 F.
∵ AD=AE,∴ DF=EF.
又∵ AB=AC,∴ BF=CF.
∴ BF - DF=CF - EF,即 BD=CE.
知2-练
3-1. [ 中考· 淄博 ] 如图,△ ABC 是等腰三角形, 点 D, E 分别在腰AC, AB 上, 且 BE =CD,连结 BD, CE.求证: BD = CE.
知2-练
知3-讲
知识点
等边三角形的定义及性质
3
1.定义 三条边都相等的三角形是等边三角形 .
知3-讲
2. 性质 (1)等边三角形的三条边都相等 .
(2)等边三角形的各个角都相等,并且每一个角都等于 60° .
(3)等边三角形是轴对称图形,它有 3 条对称轴,分别为三边的垂直平分线 .
(4)各边上的高、中线、对应的角平分线重合,且长度相等 .
知3-讲
特别解读
等边三角形是特殊的等腰三角形,具备等腰三角形的所有性质:
任意两边都可以作为腰;
任意一个角都可以作为顶角 .
知3-练
如图 13.3-5,△ ABC 是等边三角形, D、 E、 F 分别是三边 AB、 AC、 BC 上 的 点, 且 DE ⊥ AC, EF ⊥ BC,DF ⊥ AB,请计算△ DEF 各个内角的度数 .
例4
知3-练
解题秘方:紧扣等边三角形的三个内角都等于 60° 求解 .
知3-练
解:∵△ ABC 是等边三角形,
∴∠ A= ∠ B= ∠ C=60° .
∵ DE ⊥ AC, EF ⊥ BC, DF ⊥ AB,
∴∠ AED= ∠ EFC= ∠ FDB=90° .
∴∠ ADE=90°-∠ A=90°-60° =30° .
∴∠ EDF=180° -30°-90° =60°,
同理可得∠ DEF= ∠ EFD=60°,
∴△ DEF 各个内角的度数都是 60° .
知3-练
4-1. [ 中考· 鞍山 ] 如图, 直线 a ∥ b, 等边三角形 ABC 的顶点 C 在直线 b 上,∠ 2=40° ,则∠ 1 的度数为( )
A.80° B.70°
C.60° D.50°
A
知3-练
如图 13.3-6,等边三角形 ABC 的边长为 3, D 是 AC的中点,点 E 在 BC 的延长线上 . 若 DE=DB,求 CE 的长 .
例5
知3-练
解题秘方:利用等边三角形“三线合一”的性质将未知线段向已知线段转化 .
知3-练
知3-练
知3-练
5-1.如图,△ ABC 为等边三角形, AD ⊥ BC, AE=AD,则∠ ADE=_________ ° .
75
知3-练
如图 13.3-7,已知△ ABC 为等边三角形,点 D、 E分别在 BC、 AC 边上,且 AE=CD, AD 与 BE 相交于点 F.
例6
知3-练
解题秘方:利用等边三角形中边相等、角相等且为 60°的性质进行解答 .
知3-练
(1)求证:△ ABE ≌△ CAD;
知3-练
解: ∵△ ABE ≌△ CAD,
∴∠ ABE= ∠ CAD.
∵∠ BFD= ∠ ABE+ ∠ BAF,
∴∠ BFD= ∠ DAC+ ∠ BAF= ∠ BAC=60° .
(2)求∠ BFD 的度数 .
知3-练
6-1.如图, △ ABC 为等边三角形, D 为边BA 延长线上一点, 连结 CD, 以 CD 为 边 作等边三角形 CDE,连结AE, 判断 AE 与 BC 的位置关系,并说明理由 .
知5-练
解:AE∥BC.理由如下:
∵△ABC与△CDE都为等边三角形,
∴BC=AC,CD=CE,∠B=∠ACB=∠DCE=60°.
∴∠ACB+∠ACD=∠DCE+∠ACD,
即∠BCD=∠ACE.
∴△BCD≌△ACE(S.A.S.).∴∠B=∠EAC.
又∵∠B=∠ACB,∴∠EAC=∠ACB.∴AE∥BC.
等腰三角形的性质
特殊
两边相等
等腰
三角形
等边三角形
三线合一
性质
特性
三边相等,三个内角相等
等边对等角
都具有
