2025年深圳市中考备考百师助学培优课程——第2讲《一线三等角相似》 教学设计
文档属性
| 名称 | 2025年深圳市中考备考百师助学培优课程——第2讲《一线三等角相似》 教学设计 |
|
|
| 格式 | |||
| 文件大小 | 521.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-05 17:53:27 | ||
图片预览



文档简介
《一线三等角相似》教学设计
时间 2025.4.17 授课班级 九年级 7 班 授课教师 侯彦静
科目 数学 课 题 一线三等角相似
在相似三角形的判定中,两角分别相等的两个三角形相似,这种判定方法应用特别广
泛。而“一线三等角”这种特殊图形中,正是因为存在有两组对应角分别相等才会一定出
教材分析 现一对相似三角形。在不同背景中,特别是“一线三直角”这种情况在等边三角形、等腰
三角形、矩形、正方形、直角梯形以及平面直角坐标系中的应用都比较广泛。所以把握住
基本图形对于学生在复杂的图形中迅速准确的解决问题起到了关键的作用。
知识与技能:学生会借助“一线三等角”模型,找出等角,运用两组对应角分别相等的两
个三角形为相似角形的判定方法证明两个三角形相似。
教学目标 过程与方法:学生经历观察、比较、归纳的学习过程,归纳出“一线三等角”图形的基本
特征,并且能够在不同的背景中认识和把握基本模型
情感、态度与价值观:学生在学习过程中感受几何直观图形对几何学习的重要性,建立图
感。
学生在已经学习过三角形相似的基础上,再学习这一部分内容,对于绝大部分学生来
学情分析 说是可以接受的,但是还存在一部分学生基础相对薄弱,所以讲解时也需顾及到。
教学重点:运用判定方法解决“一线三等角”的相关计算与证明
重点难点
教学难点:在不同背景中识别基本模型,灵活应用模型解决问题
教学过程
学生 设计意
课堂过程 教师活动
活动 图
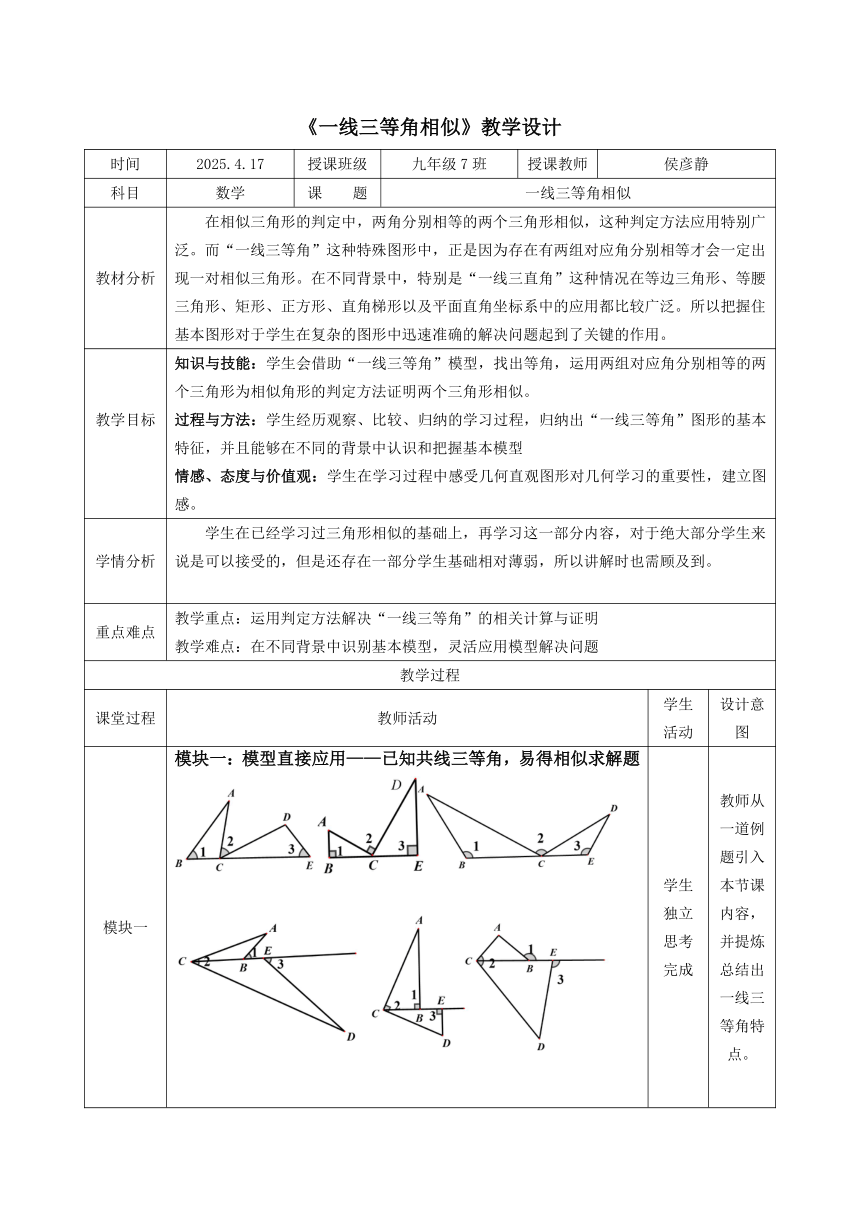
模块一:模型直接应用——已知共线三等角,易得相似求解题
教师从
一道例
题引入
学生 本节课
独立 内容,
模块一
思考 并提炼
完成 总结出
一线三
等角特
点。
(一)典例精讲
例 1:如图,在等边△ABC 中,D 为 BC 边上一点,E为 AC 边上一点,
且∠ADE=60°.
(1)求证:△ABD∽△DCE;
(2)若 BD=3,CE=2,求△ABC的边长.
例 2.(2024·齐齐哈尔中考)综合与实践
综合与实践:如图 1,这个图案是 3 世纪我国汉代的赵爽在注解《周髀
算经》时给出的,人们称它为“赵爽弦图”,受这幅图的启发,数学兴趣
小组建立了“一线三直角模型”.如图 2,在 ABC中, A 90 ,将线
段 BC绕点 B顺时针旋转90 得到线段 BD,作DE AB交 AB的延长线
于点 E.
(1)【观察感知】如图 2,通过观察,线段 AB与DE的数量关系是______;
(2)【问题解决】如图 3,连接CD并延长交 AB的延长线于点 F ,若
AB 2 , AC 6,求 BDF的面积;
(3)【类比迁移】在(2)的条件下,连接CE交 BD于点 N,则
BN
______;
BC
(二)跟进练习
1.在△ABC 中, ACB 90 , AC BC,直线MN经过点C,且
AD MN 于D, BE MN 于 E.
(1)当直线MN绕点C旋转到图 1 位置时,求证:DE AD BE;
(2)当直线MN绕点C旋转到图 2 位置时,试问:DE、 AD、 BE有
怎样的等量关系?请写出这个等量关系,并加以证明;
(3)当直线MN绕点C旋转到图 3 位置时,DE、 AD、 BE之间的等
量关系是___(直接写出答案,不需证明).
模块二:模型半构造——已知两角等值,补全第三角定模型
(一) 典例精讲
例 3 如图,在 Rt△ABC 中,,∠C=90 ∠AEB=135 , BE=3 2 ,DE⊥
BE 交 AB 于点 D ,若 DE= 2 ,则 AE 的长为___.
例 4.如图,在矩形 ABCD中,BC=4,AB=2,Rt△BEF的顶点 E在 学 生
3 教
边 CD BEF 90° EF 1上,且∠ = , = BE,DF= 5 ,则 BE= . 在 理2 4 师 巡
解 了
视,观
一 线
察学生
三 等
做法,
角 的
引导学
模块二 前 提
生 讨
下,先
论,总
(二)跟进练习 独 立
结一线
1.综合与实践 完成,
问题情境:在学习了三角形的相似后,同学们开始了对不同三角形中的 三三等
再 小
相似模型的探究. 角解题
猜想推理: 组 合
思路。
作 讨
论,最
后 展
示。
(1)如图 1,在等边△ABC 中,D为 BC边上一点,E为 AC边上一点,
ADE 60 , AB 6, BD 2,则CE ______.
问题解决:
(2)如图 2,△ABC 是等边三角形,D是 BC的中点,射线DE,DF分
别交 AB, AC于点 E,F,且 EDF 120 ,求证:DE DF.
(3)如图 3, BAC 90 ,AB 6,AC 8,D是 BC的中点,射线DE,
DE
DF分别交 AB, AC于点 E,F,且 EDF 90 ,求 的值.
DF
模块三 :模型全构造——已知单角等值,自主补全双角建体
系
(一)典例精讲
例 5.,在四边形 ABCD中,已知∠ABC=90°,AB=3,BC=4,CD=
10,DA=5 5 ,求 BD的长.
利用中
例 6.如图,在正方形 ABCD中,点 E是边CD的中点,点 F在对角线 AC
上,且 BF EF,连接 BE交 AC于点 G.若 AB 4,则线段 FG的长 考题,
为 . 让学生
学生
感受中
自己
考时如
动手
何考察
尝试,
模块三 一线三
然后
等角
小组
的,在
合作
之前的
交流
(二)跟进练习 基础上
1.【模型探究】 进行巩
如图,正方形 ABCD中,E是对角线 BD上一点,连接 AE,过点 E作
固练。
EF⊥AE,交直线 CB于点 F.
(1)如图 1,若点 F在线段 BC上,写出 EA与 EF的数量关系并加以
证明;
(2)如图 2,若点 F在线段 CB的延长线上,请直接写出线段 BC,BE
和 BF的数量关系.
【模型应用】
(3)如图 3,正方形 ABCD中,AB=4,E为 CD上一动点,连接 AE
交 BD于 F,过 F作 FH⊥AE于 F,过 H作 HG⊥BD于 G.则下列结论:
①AF=FH;②∠HAE=45°;③BD=2FG;④△CEH的周长为 8.正
确的结论有 个.
(4)如图 4,点 E是正方形 ABCD对角线 BD上一点,连接 AE,过点
E作 EF⊥AE,交线段 BC于点 F,交线段 AC于点 M,连接 AF交线段
BD于点 H.给出下列四个结论,①AE=EF;② 2 DE=CF;③S△AEM
=S△MCF;④BE=DE+ 2 BF;正确的结论有 个.
【模型变式】
(5)如图 5,在平面直角坐标系中,四边形 OBCD是正方形,且 D(0,
2),点 E是线段 OB延长线上一点,M是线段 OB上一动点(不包括点
O、B),作 MN⊥DM,垂足为 M,交∠CBE的平分线与点 N,求证:
MD=MN
(6)如图 6,在上一问的条件下,连接 DN交 BC于点 F,连接 FM,
则∠FMN和∠NMB之间有怎样的数量关系?请给出证明.
【拓展延伸】
(7)已知∠MON=90°,点 A是射线 ON上的一个定点,点 B是射线
OM上的一个动点,且满足 OB>OA.点 C在线段 OA的延长线上,且
AC=OB.如图 7,在线段 BO上截取 BE,使 BE=OA,连接 CE.若
∠OBA+∠OCE=β,当点 B在射线 OM上运动时,β的大小是否会发生
变化?如果不变,请求出这个定值;如果变化,请说明理由.
(8)如图 8,正方形 ABCD中,AD=6,点 E是对角线 AC上一点,连
接 DE,过点 E作 EF⊥ED,交 AB于点 F,连接 DF,交 AC于点 G,
将△EFG沿 EF翻折,得到△EFM,连接 DM,交 EF于点 N,若点 F
是 AB边的中点,则△EDM的面积是 .
学生
独立
一线三等角
1.. 识别一线三等角题型:在一条直线上出现了三个相等的角,一组相 完成,
等角的对边也相等(不相等)时,可证两个三角形全等(相似). 将一
巩固一
2.. 一线三等角的应用----“一线三等角”应用的三种情况. 线三
线三等
小结 ⑴ 图形中已经存在“一线三等角”,直接解題; 等角
⑵ 图形中存在“一线二等角”,补上“一等角”构造一线三等角解题; 角知
内化
⑶ 图形中只有直线上一个角,补上“二等角”构造一线三等角解題. 识。
为一
3.. 构造一线三等角的步骤:找角、定线、构全等(相似).
种解
题思
路。
板书设计
时间 2025.4.17 授课班级 九年级 7 班 授课教师 侯彦静
科目 数学 课 题 一线三等角相似
在相似三角形的判定中,两角分别相等的两个三角形相似,这种判定方法应用特别广
泛。而“一线三等角”这种特殊图形中,正是因为存在有两组对应角分别相等才会一定出
教材分析 现一对相似三角形。在不同背景中,特别是“一线三直角”这种情况在等边三角形、等腰
三角形、矩形、正方形、直角梯形以及平面直角坐标系中的应用都比较广泛。所以把握住
基本图形对于学生在复杂的图形中迅速准确的解决问题起到了关键的作用。
知识与技能:学生会借助“一线三等角”模型,找出等角,运用两组对应角分别相等的两
个三角形为相似角形的判定方法证明两个三角形相似。
教学目标 过程与方法:学生经历观察、比较、归纳的学习过程,归纳出“一线三等角”图形的基本
特征,并且能够在不同的背景中认识和把握基本模型
情感、态度与价值观:学生在学习过程中感受几何直观图形对几何学习的重要性,建立图
感。
学生在已经学习过三角形相似的基础上,再学习这一部分内容,对于绝大部分学生来
学情分析 说是可以接受的,但是还存在一部分学生基础相对薄弱,所以讲解时也需顾及到。
教学重点:运用判定方法解决“一线三等角”的相关计算与证明
重点难点
教学难点:在不同背景中识别基本模型,灵活应用模型解决问题
教学过程
学生 设计意
课堂过程 教师活动
活动 图
模块一:模型直接应用——已知共线三等角,易得相似求解题
教师从
一道例
题引入
学生 本节课
独立 内容,
模块一
思考 并提炼
完成 总结出
一线三
等角特
点。
(一)典例精讲
例 1:如图,在等边△ABC 中,D 为 BC 边上一点,E为 AC 边上一点,
且∠ADE=60°.
(1)求证:△ABD∽△DCE;
(2)若 BD=3,CE=2,求△ABC的边长.
例 2.(2024·齐齐哈尔中考)综合与实践
综合与实践:如图 1,这个图案是 3 世纪我国汉代的赵爽在注解《周髀
算经》时给出的,人们称它为“赵爽弦图”,受这幅图的启发,数学兴趣
小组建立了“一线三直角模型”.如图 2,在 ABC中, A 90 ,将线
段 BC绕点 B顺时针旋转90 得到线段 BD,作DE AB交 AB的延长线
于点 E.
(1)【观察感知】如图 2,通过观察,线段 AB与DE的数量关系是______;
(2)【问题解决】如图 3,连接CD并延长交 AB的延长线于点 F ,若
AB 2 , AC 6,求 BDF的面积;
(3)【类比迁移】在(2)的条件下,连接CE交 BD于点 N,则
BN
______;
BC
(二)跟进练习
1.在△ABC 中, ACB 90 , AC BC,直线MN经过点C,且
AD MN 于D, BE MN 于 E.
(1)当直线MN绕点C旋转到图 1 位置时,求证:DE AD BE;
(2)当直线MN绕点C旋转到图 2 位置时,试问:DE、 AD、 BE有
怎样的等量关系?请写出这个等量关系,并加以证明;
(3)当直线MN绕点C旋转到图 3 位置时,DE、 AD、 BE之间的等
量关系是___(直接写出答案,不需证明).
模块二:模型半构造——已知两角等值,补全第三角定模型
(一) 典例精讲
例 3 如图,在 Rt△ABC 中,,∠C=90 ∠AEB=135 , BE=3 2 ,DE⊥
BE 交 AB 于点 D ,若 DE= 2 ,则 AE 的长为___.
例 4.如图,在矩形 ABCD中,BC=4,AB=2,Rt△BEF的顶点 E在 学 生
3 教
边 CD BEF 90° EF 1上,且∠ = , = BE,DF= 5 ,则 BE= . 在 理2 4 师 巡
解 了
视,观
一 线
察学生
三 等
做法,
角 的
引导学
模块二 前 提
生 讨
下,先
论,总
(二)跟进练习 独 立
结一线
1.综合与实践 完成,
问题情境:在学习了三角形的相似后,同学们开始了对不同三角形中的 三三等
再 小
相似模型的探究. 角解题
猜想推理: 组 合
思路。
作 讨
论,最
后 展
示。
(1)如图 1,在等边△ABC 中,D为 BC边上一点,E为 AC边上一点,
ADE 60 , AB 6, BD 2,则CE ______.
问题解决:
(2)如图 2,△ABC 是等边三角形,D是 BC的中点,射线DE,DF分
别交 AB, AC于点 E,F,且 EDF 120 ,求证:DE DF.
(3)如图 3, BAC 90 ,AB 6,AC 8,D是 BC的中点,射线DE,
DE
DF分别交 AB, AC于点 E,F,且 EDF 90 ,求 的值.
DF
模块三 :模型全构造——已知单角等值,自主补全双角建体
系
(一)典例精讲
例 5.,在四边形 ABCD中,已知∠ABC=90°,AB=3,BC=4,CD=
10,DA=5 5 ,求 BD的长.
利用中
例 6.如图,在正方形 ABCD中,点 E是边CD的中点,点 F在对角线 AC
上,且 BF EF,连接 BE交 AC于点 G.若 AB 4,则线段 FG的长 考题,
为 . 让学生
学生
感受中
自己
考时如
动手
何考察
尝试,
模块三 一线三
然后
等角
小组
的,在
合作
之前的
交流
(二)跟进练习 基础上
1.【模型探究】 进行巩
如图,正方形 ABCD中,E是对角线 BD上一点,连接 AE,过点 E作
固练。
EF⊥AE,交直线 CB于点 F.
(1)如图 1,若点 F在线段 BC上,写出 EA与 EF的数量关系并加以
证明;
(2)如图 2,若点 F在线段 CB的延长线上,请直接写出线段 BC,BE
和 BF的数量关系.
【模型应用】
(3)如图 3,正方形 ABCD中,AB=4,E为 CD上一动点,连接 AE
交 BD于 F,过 F作 FH⊥AE于 F,过 H作 HG⊥BD于 G.则下列结论:
①AF=FH;②∠HAE=45°;③BD=2FG;④△CEH的周长为 8.正
确的结论有 个.
(4)如图 4,点 E是正方形 ABCD对角线 BD上一点,连接 AE,过点
E作 EF⊥AE,交线段 BC于点 F,交线段 AC于点 M,连接 AF交线段
BD于点 H.给出下列四个结论,①AE=EF;② 2 DE=CF;③S△AEM
=S△MCF;④BE=DE+ 2 BF;正确的结论有 个.
【模型变式】
(5)如图 5,在平面直角坐标系中,四边形 OBCD是正方形,且 D(0,
2),点 E是线段 OB延长线上一点,M是线段 OB上一动点(不包括点
O、B),作 MN⊥DM,垂足为 M,交∠CBE的平分线与点 N,求证:
MD=MN
(6)如图 6,在上一问的条件下,连接 DN交 BC于点 F,连接 FM,
则∠FMN和∠NMB之间有怎样的数量关系?请给出证明.
【拓展延伸】
(7)已知∠MON=90°,点 A是射线 ON上的一个定点,点 B是射线
OM上的一个动点,且满足 OB>OA.点 C在线段 OA的延长线上,且
AC=OB.如图 7,在线段 BO上截取 BE,使 BE=OA,连接 CE.若
∠OBA+∠OCE=β,当点 B在射线 OM上运动时,β的大小是否会发生
变化?如果不变,请求出这个定值;如果变化,请说明理由.
(8)如图 8,正方形 ABCD中,AD=6,点 E是对角线 AC上一点,连
接 DE,过点 E作 EF⊥ED,交 AB于点 F,连接 DF,交 AC于点 G,
将△EFG沿 EF翻折,得到△EFM,连接 DM,交 EF于点 N,若点 F
是 AB边的中点,则△EDM的面积是 .
学生
独立
一线三等角
1.. 识别一线三等角题型:在一条直线上出现了三个相等的角,一组相 完成,
等角的对边也相等(不相等)时,可证两个三角形全等(相似). 将一
巩固一
2.. 一线三等角的应用----“一线三等角”应用的三种情况. 线三
线三等
小结 ⑴ 图形中已经存在“一线三等角”,直接解題; 等角
⑵ 图形中存在“一线二等角”,补上“一等角”构造一线三等角解题; 角知
内化
⑶ 图形中只有直线上一个角,补上“二等角”构造一线三等角解題. 识。
为一
3.. 构造一线三等角的步骤:找角、定线、构全等(相似).
种解
题思
路。
板书设计
同课章节目录
