2025年罗湖区中考备考百师助学课程之第二十三讲《二次函数线段最值》课件
文档属性
| 名称 | 2025年罗湖区中考备考百师助学课程之第二十三讲《二次函数线段最值》课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-05 17:53:27 | ||
图片预览








文档简介
(共30张PPT)
罗湖区中考备考“百师助学”课程
二次函数中的线段最值问题
执教者:黎幼彦老师 桂园中学
一.知识点梳理
中考题中二次函数的综合题,目的是考查考生的综合能力.一般第(1)问求函数的解析式,考查考生对二次函数概念的理解及基本计算;第(2)问求线段的和、差,比,周长或面积的最值,考查考生对函数的图象和性质、坐标特点的理解,也初步培养考生“解析几何”理念,培养学生转化问题的能力,考查考生对相似和特殊图形的边、角关系的理解能力.
二次函数的一般式
y=ax2+bx+c(a≠0)
顶点坐标为:
对称轴是直线
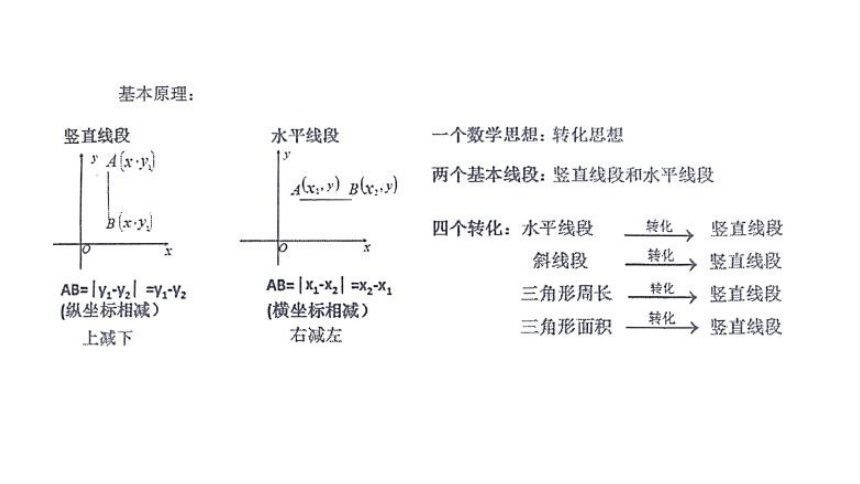
铅垂线段的求法——横坐标相同
水平线段的求法——纵坐标相同
模块一
(1)∵直线L:y=kx﹣1过点A(﹣1,0),
∴0=﹣k﹣1,
解得k=﹣1,
即直线L的解析式为y=﹣x﹣1;
模块二
斜线段的求法——化斜为直
模块三
面积,周长——转化为竖直线段
5
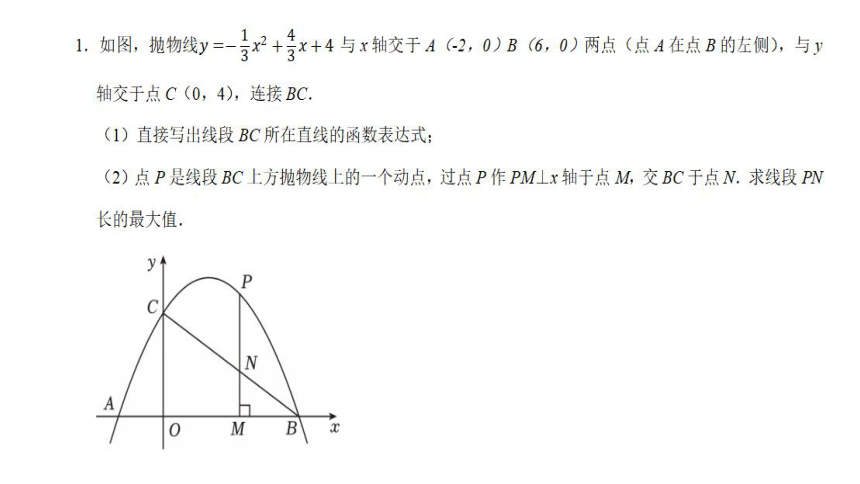
6.如图,在平面直角坐标系中,抛物线y=ax2+bx+2过点(1,3),且交x轴于点A(﹣1,0),B两点,交y轴于点C.
(1)求抛物线的表达式;
(2)点P是直线BC上方抛物线上的一动点,过点P作PD⊥BC于点D,过点P作y轴的平行线交直线BC于点E,求△PDE周长的最大值及此时点P的坐标;
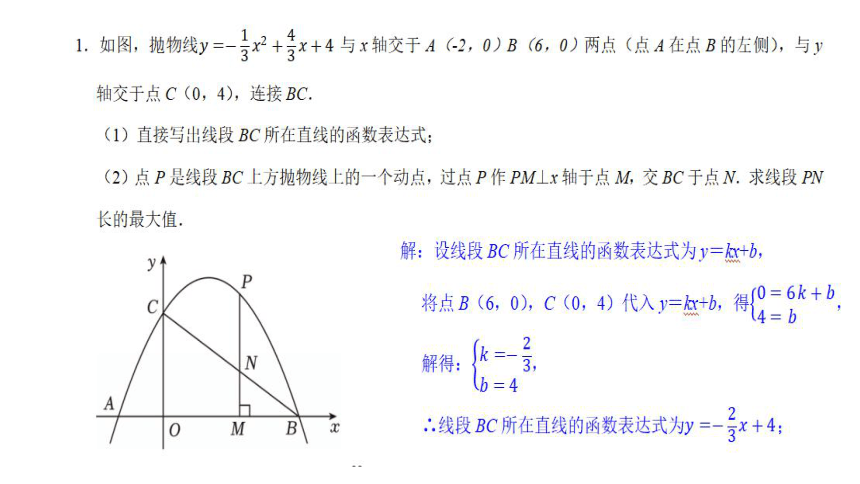
6.如图,在平面直角坐标系中,抛物线y=ax2+bx+2过点(1,3),且交x轴于点A(﹣1,0),B两点,交y轴于点C.
(1)求抛物线的表达式;
(2)点P是直线BC上方抛物线上的一动点,过点P作PD⊥BC于点D,过点P作y轴的平行线交直线BC于点E,求△PDE周长的最大值及此时点P的坐标;
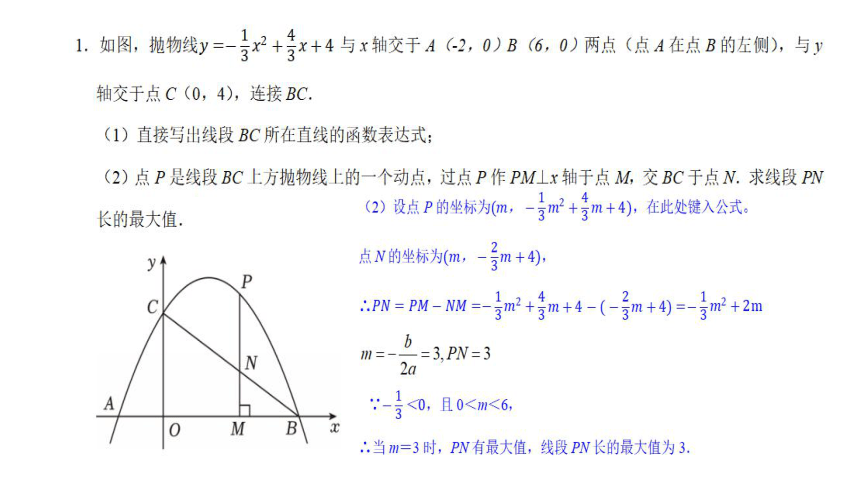
6.如图,在平面直角坐标系中,抛物线y=ax2+bx+2过点(1,3),且交x轴于点A(﹣1,0),B两点,交y轴于点C.
(2)点P是直线BC上方抛物线上的一动点,过点P作PD⊥BC于点D,过点P作y轴的平行线交直线BC于点E,求△PDE周长的最大值及此时点P的坐标;
6.如图,在平面直角坐标系中,抛物线y=ax2+bx+2过点(1,3),且交x轴于点A(﹣1,0),B两点,交y轴于点C.
(2)点P是直线BC上方抛物线上的一动点,过点P作PD⊥BC于点D,过点P作y轴的平行线交直线BC于点E,求△PDE周长的最大值及此时点P的坐标;
1.如图,抛物线 y=﹣0.5x2+x+4与直线y=x+2交于A(-2,0),D(2,4)两点,与x轴交于另外一点B(4,0),与y轴交于点C。AD交于Y轴于点H。点P是直线AD上方抛物线上的动点(不与A,D两点重合),以P为圆心作 P,使得 P与直线AD相切,求圆 P的最大面积。
1.如图,抛物线 y=﹣0.5x2+x+4与直线y=x+2交于A(-2,0),D(2,4)两点,与x轴交于另外一点B(4,0),与y轴交于点C。AD交于Y轴于点H。点P是直线AD上方抛物线上的动点(不与A,D两点重合),以P为圆心作 P,使得 P与直线AD相切,求圆 P的最大面积。
总结
利用二次函数求线段最值
方法步骤:
①根据点在图象上满足函数解析式,设出动点坐标;
②根据宽高公式、两点间距离公式等表示出三角形的面积、周长,线段长度或比等;
③根据表示出的函数关系式和动点范围求出最值.
(借助相似三角形,三角函数进行线段转化)
课后作业
2.如图,抛物线y = ﹣0.5x2 +bx+c与x轴交于点A(﹣1,0)和点B(4,0),
与y轴交于点C,连接BC,点P是线段BC上的动点(与点B,C不重合),连接AP
并延长AP交抛物线于点Q,连接CQ,BQ,设点Q的横坐标为m.
(1)求抛物线的解析式和点C的坐标;
(2)当△BCQ的面积等于2时,求m的值;
(3)在点P运动过程中, 是否存在最大值?若存在,求出最大值;若不存在,请说明理由
罗湖区中考备考“百师助学”课程
二次函数中的线段最值问题
执教者:黎幼彦老师 桂园中学
一.知识点梳理
中考题中二次函数的综合题,目的是考查考生的综合能力.一般第(1)问求函数的解析式,考查考生对二次函数概念的理解及基本计算;第(2)问求线段的和、差,比,周长或面积的最值,考查考生对函数的图象和性质、坐标特点的理解,也初步培养考生“解析几何”理念,培养学生转化问题的能力,考查考生对相似和特殊图形的边、角关系的理解能力.
二次函数的一般式
y=ax2+bx+c(a≠0)
顶点坐标为:
对称轴是直线
铅垂线段的求法——横坐标相同
水平线段的求法——纵坐标相同
模块一
(1)∵直线L:y=kx﹣1过点A(﹣1,0),
∴0=﹣k﹣1,
解得k=﹣1,
即直线L的解析式为y=﹣x﹣1;
模块二
斜线段的求法——化斜为直
模块三
面积,周长——转化为竖直线段
5
6.如图,在平面直角坐标系中,抛物线y=ax2+bx+2过点(1,3),且交x轴于点A(﹣1,0),B两点,交y轴于点C.
(1)求抛物线的表达式;
(2)点P是直线BC上方抛物线上的一动点,过点P作PD⊥BC于点D,过点P作y轴的平行线交直线BC于点E,求△PDE周长的最大值及此时点P的坐标;
6.如图,在平面直角坐标系中,抛物线y=ax2+bx+2过点(1,3),且交x轴于点A(﹣1,0),B两点,交y轴于点C.
(1)求抛物线的表达式;
(2)点P是直线BC上方抛物线上的一动点,过点P作PD⊥BC于点D,过点P作y轴的平行线交直线BC于点E,求△PDE周长的最大值及此时点P的坐标;
6.如图,在平面直角坐标系中,抛物线y=ax2+bx+2过点(1,3),且交x轴于点A(﹣1,0),B两点,交y轴于点C.
(2)点P是直线BC上方抛物线上的一动点,过点P作PD⊥BC于点D,过点P作y轴的平行线交直线BC于点E,求△PDE周长的最大值及此时点P的坐标;
6.如图,在平面直角坐标系中,抛物线y=ax2+bx+2过点(1,3),且交x轴于点A(﹣1,0),B两点,交y轴于点C.
(2)点P是直线BC上方抛物线上的一动点,过点P作PD⊥BC于点D,过点P作y轴的平行线交直线BC于点E,求△PDE周长的最大值及此时点P的坐标;
1.如图,抛物线 y=﹣0.5x2+x+4与直线y=x+2交于A(-2,0),D(2,4)两点,与x轴交于另外一点B(4,0),与y轴交于点C。AD交于Y轴于点H。点P是直线AD上方抛物线上的动点(不与A,D两点重合),以P为圆心作 P,使得 P与直线AD相切,求圆 P的最大面积。
1.如图,抛物线 y=﹣0.5x2+x+4与直线y=x+2交于A(-2,0),D(2,4)两点,与x轴交于另外一点B(4,0),与y轴交于点C。AD交于Y轴于点H。点P是直线AD上方抛物线上的动点(不与A,D两点重合),以P为圆心作 P,使得 P与直线AD相切,求圆 P的最大面积。
总结
利用二次函数求线段最值
方法步骤:
①根据点在图象上满足函数解析式,设出动点坐标;
②根据宽高公式、两点间距离公式等表示出三角形的面积、周长,线段长度或比等;
③根据表示出的函数关系式和动点范围求出最值.
(借助相似三角形,三角函数进行线段转化)
课后作业
2.如图,抛物线y = ﹣0.5x2 +bx+c与x轴交于点A(﹣1,0)和点B(4,0),
与y轴交于点C,连接BC,点P是线段BC上的动点(与点B,C不重合),连接AP
并延长AP交抛物线于点Q,连接CQ,BQ,设点Q的横坐标为m.
(1)求抛物线的解析式和点C的坐标;
(2)当△BCQ的面积等于2时,求m的值;
(3)在点P运动过程中, 是否存在最大值?若存在,求出最大值;若不存在,请说明理由
同课章节目录
