2025年深圳市中考备考百师助学培优课程——第5讲《圆与相似》 模块一 课件
文档属性
| 名称 | 2025年深圳市中考备考百师助学培优课程——第5讲《圆与相似》 模块一 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 488.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-05 00:00:00 | ||
图片预览


文档简介
(共7张PPT)
罗湖区2025中考备考“百师助学”课程
课题:圆与相似
模块一 圆中的A字型相似
南方科技大学附属罗湖中学
曹美玉
模块一: 圆中的A字型相似
内容讲解(A 字模型)
①
②
③
△ADE~△ABC
平行线
共角
方向相同
模块一: 圆中的A字型相似
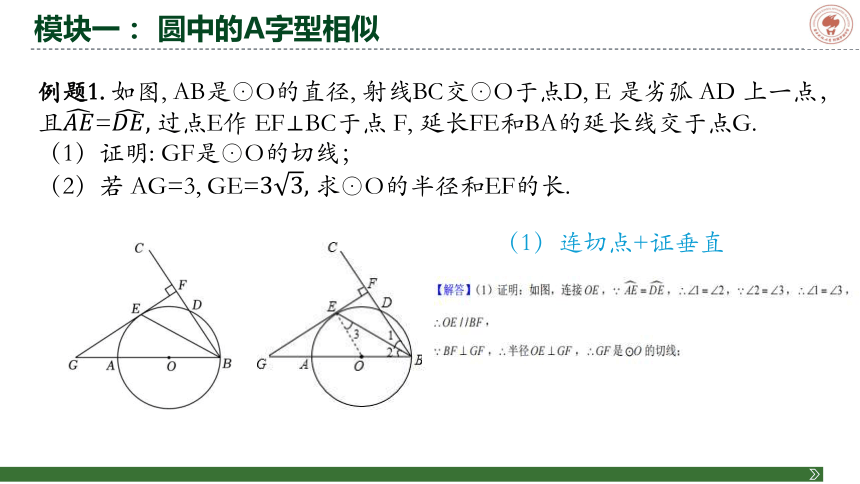
例题1. 如图, AB是⊙O的直径, 射线BC交⊙O于点D, E 是劣弧 AD 上一点,且=过点E作 EF BC于点 F, 延长FE和BA的延长线交于点G.
(1)证明: GF是⊙O的切线;
(2)若 AG=3, GE=求⊙O的半径和EF的长.
(1)连切点+证垂直
模块一: 圆中的A字型相似
例题1. 如图, AB是⊙O的直径, 射线BC交⊙O于点D, E 是劣弧 AD 上一点,且=过点E作 EF BC于点 F, 延长FE和BA的延长线交于点G.
(1)证明: GF是⊙O的切线;
(2)若 AG=3, GE=求⊙O的半径和EF的长.
(2)勾股定理求解半径
A字相似求EF的长
△GEO~△GFB
3
模块一: 圆中的A字型相似
例题2. 如图, 在△ABC中, AB=AC, 以AB为直径的⊙O交BC于点D, 点P在BC 的延长线上, 且 ∠BAC=2∠P.
(1)求证: 直线AP是⊙O的切线;
(2)若BC=6, tanP=, 求⊙O的半径长及 tan∠PAC的值.
(1)证垂直,得切线
模块一: 圆中的A字型相似
例题2. 如图, 在△ABC中, AB=AC, 以AB为直径的⊙O交BC于点D, 点P在BC 的延长线上, 且 ∠BAC=2∠P.
(1)求证: 直线AP是⊙O的切线;
(2)若BC=6, tanP=, 求⊙O的半径长及 tan∠PAC的值.
(2)勾股定理求解半径
A字相似求三角函数的值
△PEC~△PAE
3
4
谢谢!
罗湖区2025中考备考“百师助学”课程
课题:圆与相似
模块一 圆中的A字型相似
南方科技大学附属罗湖中学
曹美玉
模块一: 圆中的A字型相似
内容讲解(A 字模型)
①
②
③
△ADE~△ABC
平行线
共角
方向相同
模块一: 圆中的A字型相似
例题1. 如图, AB是⊙O的直径, 射线BC交⊙O于点D, E 是劣弧 AD 上一点,且=过点E作 EF BC于点 F, 延长FE和BA的延长线交于点G.
(1)证明: GF是⊙O的切线;
(2)若 AG=3, GE=求⊙O的半径和EF的长.
(1)连切点+证垂直
模块一: 圆中的A字型相似
例题1. 如图, AB是⊙O的直径, 射线BC交⊙O于点D, E 是劣弧 AD 上一点,且=过点E作 EF BC于点 F, 延长FE和BA的延长线交于点G.
(1)证明: GF是⊙O的切线;
(2)若 AG=3, GE=求⊙O的半径和EF的长.
(2)勾股定理求解半径
A字相似求EF的长
△GEO~△GFB
3
模块一: 圆中的A字型相似
例题2. 如图, 在△ABC中, AB=AC, 以AB为直径的⊙O交BC于点D, 点P在BC 的延长线上, 且 ∠BAC=2∠P.
(1)求证: 直线AP是⊙O的切线;
(2)若BC=6, tanP=, 求⊙O的半径长及 tan∠PAC的值.
(1)证垂直,得切线
模块一: 圆中的A字型相似
例题2. 如图, 在△ABC中, AB=AC, 以AB为直径的⊙O交BC于点D, 点P在BC 的延长线上, 且 ∠BAC=2∠P.
(1)求证: 直线AP是⊙O的切线;
(2)若BC=6, tanP=, 求⊙O的半径长及 tan∠PAC的值.
(2)勾股定理求解半径
A字相似求三角函数的值
△PEC~△PAE
3
4
谢谢!
同课章节目录
