2025年深圳市中考备考百师助学培优课程——第10讲《全等图形——旋转构造》 课件
文档属性
| 名称 | 2025年深圳市中考备考百师助学培优课程——第10讲《全等图形——旋转构造》 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 235.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-05 17:53:27 | ||
图片预览



文档简介
(共11张PPT)
第10讲 全等图形
——旋转构造
授课人:黄湘升 单位:翠园东晓中学
罗湖区中考备考“百师助学”课程
一、知识梳理
全等图形的旋转向来都是数学中考的热点,它往往以填空题和解答题的压轴题形式出现,此题型涉及知识面广,对学生的综合能力要求高,是我们复习的重点和难点。
旋转的本质是图形的点在同心圆上作同步运动,“集体行动,步调一致”。图形旋转后,对应边、对应角分别对应相等。
通过旋转构造我们构建全等图形、直角三角形或等边三角形等,从而解决线段长短或角度大小等问题。
旋转
“对应边”相等
等腰
等边
构建旋转
对应边相等
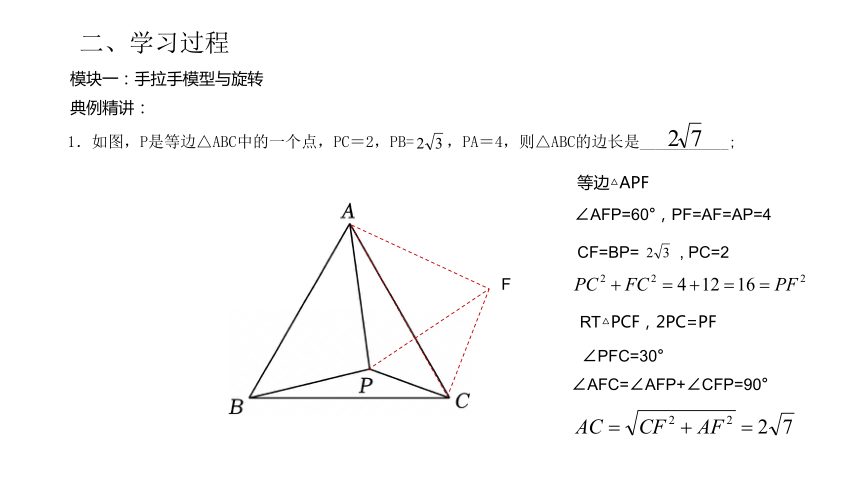
1.如图,P是等边△ABC中的一个点,PC=2,PB= ,PA=4,则△ABC的边长是___________;
模块一:手拉手模型与旋转
二、学习过程
典例精讲:
F
等边△APF
∠AFP=60°,PF=AF=AP=4
CF=BP= , PC=2
RT△PCF,2PC=PF
∠PFC=30°
∠AFC=∠AFP+∠CFP=90°
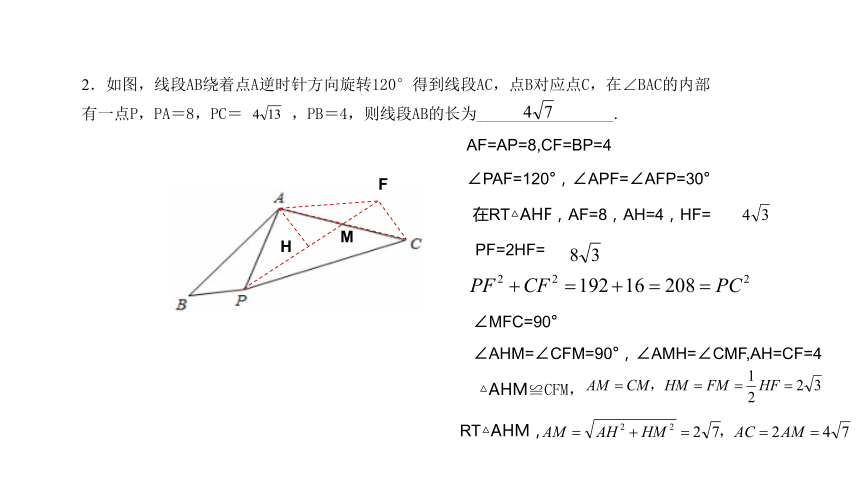
2.如图,线段AB绕着点A逆时针方向旋转120°得到线段AC,点B对应点C,在∠BAC的内部有一点P,PA=8,PC= ,PB=4,则线段AB的长为_________________.
F
M
H
在RT△AHF,AF=8,AH=4,HF=
PF=2HF=
AF=AP=8,CF=BP=4
∠PAF=120°,∠APF=∠AFP=30°
∠MFC=90°
∠AHM=∠CFM=90°,∠AMH=∠CMF,AH=CF=4
△AHM≌CFM,
RT△AHM,
1.如图,在△ABC中,∠BAC=90°,AB=AC,点D和点E 均在边BC上,且∠DAE=45°.若 BD=4,CE=5,则DE=___________________;
典例精讲:
模块二:半角模型与旋转
F
∠FBD=∠FBA+∠ABD=∠C+∠ABD=90°
RT△BFD中,
△AFD≌△FAD
ED=FD=
2.如图,在正方形ABCD中,点E在AB上,连接DE,作等腰直角三角形DEF,∠DEF=90°,连接AC,AC交DE于点G,交DF于点H.若AG=4,CH=3,则DG的长为__________.
K
T
RT△HCK,HK=5
△DGH≌△DKH,GH=KH=5
AC=AG+GH+CH=12
RT△TGD,
典例精讲:
模块三:对角互补与旋转
1.如图,四边形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD的面积为 .
F
12.5
RT△ACF,AC=AF=5
典例精讲:
模块三:全等对角互补与旋转
1.如图,在四边形ABCD中,AB=AD=2,∠DAB=∠DCA=60°,则CD+CB的最大值是 .
F
连接BD,等边△ABD
∠ABD=∠DAB=∠DCA=60°
点A、B、C和D四点共圆
∠ABC+∠ADC=180°
AC=FC,∠ACF=60°,等边△ACF
点F、D和C三点共线
CD+CB=CD+DF=CF=AC
当AC为直径时,CD+CB=AC有最大值
1.见腰(或者等边)想旋转;
2.旋转角度一般为60°、90°或者120°;
小结:
感谢聆听,再见。
第10讲 全等图形
——旋转构造
授课人:黄湘升 单位:翠园东晓中学
罗湖区中考备考“百师助学”课程
一、知识梳理
全等图形的旋转向来都是数学中考的热点,它往往以填空题和解答题的压轴题形式出现,此题型涉及知识面广,对学生的综合能力要求高,是我们复习的重点和难点。
旋转的本质是图形的点在同心圆上作同步运动,“集体行动,步调一致”。图形旋转后,对应边、对应角分别对应相等。
通过旋转构造我们构建全等图形、直角三角形或等边三角形等,从而解决线段长短或角度大小等问题。
旋转
“对应边”相等
等腰
等边
构建旋转
对应边相等
1.如图,P是等边△ABC中的一个点,PC=2,PB= ,PA=4,则△ABC的边长是___________;
模块一:手拉手模型与旋转
二、学习过程
典例精讲:
F
等边△APF
∠AFP=60°,PF=AF=AP=4
CF=BP= , PC=2
RT△PCF,2PC=PF
∠PFC=30°
∠AFC=∠AFP+∠CFP=90°
2.如图,线段AB绕着点A逆时针方向旋转120°得到线段AC,点B对应点C,在∠BAC的内部有一点P,PA=8,PC= ,PB=4,则线段AB的长为_________________.
F
M
H
在RT△AHF,AF=8,AH=4,HF=
PF=2HF=
AF=AP=8,CF=BP=4
∠PAF=120°,∠APF=∠AFP=30°
∠MFC=90°
∠AHM=∠CFM=90°,∠AMH=∠CMF,AH=CF=4
△AHM≌CFM,
RT△AHM,
1.如图,在△ABC中,∠BAC=90°,AB=AC,点D和点E 均在边BC上,且∠DAE=45°.若 BD=4,CE=5,则DE=___________________;
典例精讲:
模块二:半角模型与旋转
F
∠FBD=∠FBA+∠ABD=∠C+∠ABD=90°
RT△BFD中,
△AFD≌△FAD
ED=FD=
2.如图,在正方形ABCD中,点E在AB上,连接DE,作等腰直角三角形DEF,∠DEF=90°,连接AC,AC交DE于点G,交DF于点H.若AG=4,CH=3,则DG的长为__________.
K
T
RT△HCK,HK=5
△DGH≌△DKH,GH=KH=5
AC=AG+GH+CH=12
RT△TGD,
典例精讲:
模块三:对角互补与旋转
1.如图,四边形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD的面积为 .
F
12.5
RT△ACF,AC=AF=5
典例精讲:
模块三:全等对角互补与旋转
1.如图,在四边形ABCD中,AB=AD=2,∠DAB=∠DCA=60°,则CD+CB的最大值是 .
F
连接BD,等边△ABD
∠ABD=∠DAB=∠DCA=60°
点A、B、C和D四点共圆
∠ABC+∠ADC=180°
AC=FC,∠ACF=60°,等边△ACF
点F、D和C三点共线
CD+CB=CD+DF=CF=AC
当AC为直径时,CD+CB=AC有最大值
1.见腰(或者等边)想旋转;
2.旋转角度一般为60°、90°或者120°;
小结:
感谢聆听,再见。
同课章节目录
