2025年深圳市中考备考百师助学培优课程——第17讲《建立平面直角坐标系解决几何问题》课件
文档属性
| 名称 | 2025年深圳市中考备考百师助学培优课程——第17讲《建立平面直角坐标系解决几何问题》课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 767.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-05 17:53:27 | ||
图片预览








文档简介
(共22张PPT)
建立平面直角坐标系 解决几何问题
深圳市罗湖区翠园实验学校 陈浩
罗湖区初中数学2025届中考备考“百师助学”课程
一、知识梳理
《义务教育数学课程标准(2022)年版》指出初中阶段图形与几何领域包括“图形的性质”“图形的变化”和“图形与坐标”三个主题。其中“图形与坐标”强调数形结合,用代数方法研究图形,在平面直角坐标系中用坐标表示图形上点的位置,用坐标法分析和解决实际问题。建立平面直角坐标系是研究函数问题的重要一步,反过来从函数的角度去研究几何问题也是很重要的。初中阶段的几何题里大多是以矩形、正方形、直角三角形、等腰三角形等为背景,而这些几何图形都能通过建立平面直角坐标系来解决问题,从而做到几何问题代数化。这种“建立平面直角坐标系解决几何问题”简称“建系法”的方法既增加了代数推理,又增强了几何直观,从而达到数与形的完美统一。
1.两点间距离公式
2.中点坐标公式
1.知识储备
o
B(x2,y2)
A(x1,y1)
C
y
x
由已知得
3.一次函数求“k”
o
B(x2,y2)
A(x1,y1)
y
x
4.关于一次函数“k”的重要结论
模块一:建系法的认识
二、学习过程
问题1:什么是建系法?
在初中数学中,建系法(即建立坐标系的方法)是一种通过构造平面直角坐标系,将几何问题转化为代数问题来解决的策略。它属于数形结合的思想,常用于简化几何证明或计算。
问题2:什么题型适合建系?
(1)存在直角(题目中有正方形、矩形或直角三角形等)
(2)容易构造直角(题目中有等腰三角形、正三角形、菱形等)
(3)给了一些线段长度(最好是两条直角边的长度,方便表示出坐标)
问题3:坐标原点如何选取?
y
x
o
y
x
o
y
x
o
y
x
o
y
x
o
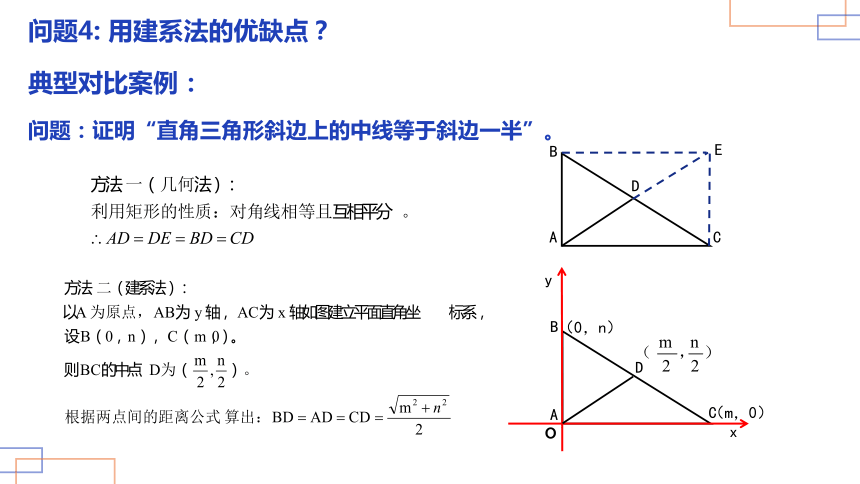
问题4: 用建系法的优缺点?
典型对比案例:
问题:证明“直角三角形斜边上的中线等于斜边一半”。
y
x
o
A
B
C
D
A
B
C
D
(m,0)
(0,n)
E
问题4: 用建系法的优缺点?
优点:
①程序化操作
步骤固定:建系 → 标坐标 → 求解析式 → 计算,适合不擅长几何思维的学生。
②化抽象为具体
将几何图形中的点、线、角等抽象元素用具体的坐标和方程表示,使问题更直观。
③通用性强
适用于大多数规则图形(如三角形、矩形、菱形等),尤其是对称性或垂直性明显的图形。
例如:求非特殊三角形面积时,直接利用顶点坐标和面积公式(如铅锤法)比几何分割更快捷。
④简化动态问题
对动点轨迹、最值问题可通过函数或方程分析,避免复杂几何构造。
例如:求线段最小值时,可转化为求二次函数顶点或两点间距离。
问题4: 用建系法的优缺点?
缺点:
①依赖坐标系的选择
坐标系选取不当(如斜放图形)会导致坐标复杂,计算量增大。
例如:若将三角形的边与坐标轴不平行,坐标表达式会变得繁琐。
②计算易出错
涉及多步代数运算(如距离公式、斜率、联立方程等),容易因粗心出错。
例如:验证两条直线垂直时,需计算斜率乘积是否为-1,符号错误可能导致结论错误。
③丧失几何直观
过度依赖代数可能掩盖几何本质,不利于培养空间想象能力。
例如:用坐标法证明“勾股定理”虽可行,但不如几何拼图法直观。
④不适用于所有问题
对非规则图形(如任意四边形)或求图形的角度关系可能效率低下。
模块一:建系法的认识
二、学习过程
问题1:什么是建系法?
问题2:什么题型适合建系?
问题3:坐标原点如何选取?
问题4: 用建系法的优缺点?
what?
how?
why
模块二:建系法在矩形下的运用
二、学习过程
典例精讲
x
y
(0,0)
(4,0)
(4,4)
(0,4)
(2,4)
(4,2)
建系
标坐标
求解析式
计算
典例精讲
x
y
建系
标坐标
求解析式
计算
(0,0)
(6,0)
(0,6)
(6,6)
(6,2)
(3,3)
典例精讲
x
y
M
P
N
建系
标坐标
求解析式
计算
解答:以B点为原点,AB为y轴,如图建立平面直角坐标系,
则B(0,0),C(6,0),D(6,6),A(0,6),E(2,6),F(1,3)
(0,6)
(6,0)
(6,6)
(0,0)
(2,6)
(1,6)
(5,5)
模块二:建系法在矩形下的运用
二、学习过程
模块三:建系法在三角形下的运用
二、学习过程
典例精讲
x
y
建系
标坐标
计算
(0,0)
(2,0)
(0,1)
(2,2)
(3,2)
典例精讲
典例精讲
x
y
解答:
以D点为原点,DB为y轴建系,如图所示,
建系
标坐标
计算
则A(1,0),E(2,0),B(0,2)
过C点作CF⊥BD,构造三垂直全等,即△ABD≌△BCF,
CF=BD=2,BF=AD=1,
∴C点坐标为(-2,1)
∴由两点间的距离公式可
得CE=
(0,0)
(1,0)
(2,0)
(0,2)
(-2,1)
F
典例精讲
x
y
A
B
C
D
O
K
建系
标坐标
求解析式
计算
(-4,0)
(4,0)
(0,6)
建立平面直角坐标系解决几何问题
深圳市罗湖区翠园实验学校
陈浩
罗湖区初中数学2025届中考备考“百师助学”课程
我思故我在
在中考这场思维坐标系的构建中,愿同学们传承笛卡尔的三种力量:
一是像他病中演算的坚持力(态度):
坐标系不是顿悟,是夜以继日描点的轨迹;
二是学他构建几何代数的整合力(方法):
用横轴串联知识,用纵轴贯通方法;
三是效他打破常规的破界力(创新):
当旧公式解不开新题时,记得你本就是坐标系的原点,
拥有重新定义方向的权利。
建立平面直角坐标系 解决几何问题
深圳市罗湖区翠园实验学校 陈浩
罗湖区初中数学2025届中考备考“百师助学”课程
一、知识梳理
《义务教育数学课程标准(2022)年版》指出初中阶段图形与几何领域包括“图形的性质”“图形的变化”和“图形与坐标”三个主题。其中“图形与坐标”强调数形结合,用代数方法研究图形,在平面直角坐标系中用坐标表示图形上点的位置,用坐标法分析和解决实际问题。建立平面直角坐标系是研究函数问题的重要一步,反过来从函数的角度去研究几何问题也是很重要的。初中阶段的几何题里大多是以矩形、正方形、直角三角形、等腰三角形等为背景,而这些几何图形都能通过建立平面直角坐标系来解决问题,从而做到几何问题代数化。这种“建立平面直角坐标系解决几何问题”简称“建系法”的方法既增加了代数推理,又增强了几何直观,从而达到数与形的完美统一。
1.两点间距离公式
2.中点坐标公式
1.知识储备
o
B(x2,y2)
A(x1,y1)
C
y
x
由已知得
3.一次函数求“k”
o
B(x2,y2)
A(x1,y1)
y
x
4.关于一次函数“k”的重要结论
模块一:建系法的认识
二、学习过程
问题1:什么是建系法?
在初中数学中,建系法(即建立坐标系的方法)是一种通过构造平面直角坐标系,将几何问题转化为代数问题来解决的策略。它属于数形结合的思想,常用于简化几何证明或计算。
问题2:什么题型适合建系?
(1)存在直角(题目中有正方形、矩形或直角三角形等)
(2)容易构造直角(题目中有等腰三角形、正三角形、菱形等)
(3)给了一些线段长度(最好是两条直角边的长度,方便表示出坐标)
问题3:坐标原点如何选取?
y
x
o
y
x
o
y
x
o
y
x
o
y
x
o
问题4: 用建系法的优缺点?
典型对比案例:
问题:证明“直角三角形斜边上的中线等于斜边一半”。
y
x
o
A
B
C
D
A
B
C
D
(m,0)
(0,n)
E
问题4: 用建系法的优缺点?
优点:
①程序化操作
步骤固定:建系 → 标坐标 → 求解析式 → 计算,适合不擅长几何思维的学生。
②化抽象为具体
将几何图形中的点、线、角等抽象元素用具体的坐标和方程表示,使问题更直观。
③通用性强
适用于大多数规则图形(如三角形、矩形、菱形等),尤其是对称性或垂直性明显的图形。
例如:求非特殊三角形面积时,直接利用顶点坐标和面积公式(如铅锤法)比几何分割更快捷。
④简化动态问题
对动点轨迹、最值问题可通过函数或方程分析,避免复杂几何构造。
例如:求线段最小值时,可转化为求二次函数顶点或两点间距离。
问题4: 用建系法的优缺点?
缺点:
①依赖坐标系的选择
坐标系选取不当(如斜放图形)会导致坐标复杂,计算量增大。
例如:若将三角形的边与坐标轴不平行,坐标表达式会变得繁琐。
②计算易出错
涉及多步代数运算(如距离公式、斜率、联立方程等),容易因粗心出错。
例如:验证两条直线垂直时,需计算斜率乘积是否为-1,符号错误可能导致结论错误。
③丧失几何直观
过度依赖代数可能掩盖几何本质,不利于培养空间想象能力。
例如:用坐标法证明“勾股定理”虽可行,但不如几何拼图法直观。
④不适用于所有问题
对非规则图形(如任意四边形)或求图形的角度关系可能效率低下。
模块一:建系法的认识
二、学习过程
问题1:什么是建系法?
问题2:什么题型适合建系?
问题3:坐标原点如何选取?
问题4: 用建系法的优缺点?
what?
how?
why
模块二:建系法在矩形下的运用
二、学习过程
典例精讲
x
y
(0,0)
(4,0)
(4,4)
(0,4)
(2,4)
(4,2)
建系
标坐标
求解析式
计算
典例精讲
x
y
建系
标坐标
求解析式
计算
(0,0)
(6,0)
(0,6)
(6,6)
(6,2)
(3,3)
典例精讲
x
y
M
P
N
建系
标坐标
求解析式
计算
解答:以B点为原点,AB为y轴,如图建立平面直角坐标系,
则B(0,0),C(6,0),D(6,6),A(0,6),E(2,6),F(1,3)
(0,6)
(6,0)
(6,6)
(0,0)
(2,6)
(1,6)
(5,5)
模块二:建系法在矩形下的运用
二、学习过程
模块三:建系法在三角形下的运用
二、学习过程
典例精讲
x
y
建系
标坐标
计算
(0,0)
(2,0)
(0,1)
(2,2)
(3,2)
典例精讲
典例精讲
x
y
解答:
以D点为原点,DB为y轴建系,如图所示,
建系
标坐标
计算
则A(1,0),E(2,0),B(0,2)
过C点作CF⊥BD,构造三垂直全等,即△ABD≌△BCF,
CF=BD=2,BF=AD=1,
∴C点坐标为(-2,1)
∴由两点间的距离公式可
得CE=
(0,0)
(1,0)
(2,0)
(0,2)
(-2,1)
F
典例精讲
x
y
A
B
C
D
O
K
建系
标坐标
求解析式
计算
(-4,0)
(4,0)
(0,6)
建立平面直角坐标系解决几何问题
深圳市罗湖区翠园实验学校
陈浩
罗湖区初中数学2025届中考备考“百师助学”课程
我思故我在
在中考这场思维坐标系的构建中,愿同学们传承笛卡尔的三种力量:
一是像他病中演算的坚持力(态度):
坐标系不是顿悟,是夜以继日描点的轨迹;
二是学他构建几何代数的整合力(方法):
用横轴串联知识,用纵轴贯通方法;
三是效他打破常规的破界力(创新):
当旧公式解不开新题时,记得你本就是坐标系的原点,
拥有重新定义方向的权利。
同课章节目录
