2025年深圳市中考备考百师助学培优课程——第13讲《新函数综合题探究》课件
文档属性
| 名称 | 2025年深圳市中考备考百师助学培优课程——第13讲《新函数综合题探究》课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-05 00:00:00 | ||
图片预览







文档简介
(共31张PPT)
第13讲 新函数图像探究题
罗湖区中考备考“百师助学”课程
深圳市桂园中学 郭培香
中线等分三角形面积
一、知识要点
新函数图像探究题是近些年中考数学的一种新题型,在北京、河南、重庆等地的中考数学试卷中已有出现,近年来越来越频繁地出现在深圳的中考数学试卷中。
新函数图像探究题是建立在学生已经学习的一次函数、反比例函数和二次函数基础之上,将基本函数进行组合、变形、平移等形成新的函数,是对函数图像与性质的综合运用。
在初中阶段的函数学习中,我们经历了“确定函数的表达式﹣﹣利用函数图象研究其性质一一运用函数解决问题”的学习过程.新函数图像的探究题的学习也是同样的过程,作出函数图像是解题的关键。
中线等分三角形面积
一、知识要点
函数图象性质的探究题常见问题:
①求变量的取值范围:根据解析式中分式、二次根式等有意义的条件,列出不等式(组)进行求解;
②描点、连线画函数图象:用平滑的曲线依次连接各点即可;
③写函数的相关性质:根据函数图象,从最值、增减性、对称性、特殊点等方面入手即可;
④函数与方程或不等式综合考查,观察函数图像求值或取值范围,理解函数图像的交点的坐标与方程的解的关系,掌握在同一坐标系中不同函数的值的大小与函数图像的位置关系是解题的关键;
⑤函数与几何综合、函数与实践探究及新定义的考查。
1.作一条线段等于已知线段:
2.作已知角的平分线:
3.作已知线段的垂直平1.作一条线段等于已知线段:
2.作已知角的平分线:
3.作已知线段的垂直平分线:
4.作一个角等于已知角:
5.过一点作已知直线的垂线【点在线上、点在线外】。分线:
4.作一个角等于已知角:
5.过一点作已知直线的垂线【点在线上、点在线外】。
模块一:新函数的四种常见类型
一、绝对值函数
二、分段函数
三、高次函数
四、组合函数
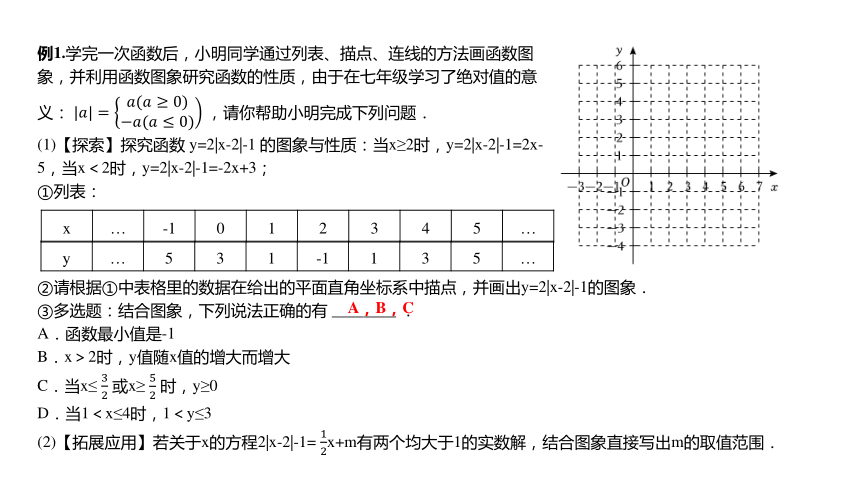
例1.学完一次函数后,小明同学通过列表、描点、连线的方法画函数图象,并利用函数图象研究函数的性质,由于在七年级学习了绝对值的意义: ,请你帮助小明完成下列问题.
(1)【探索】探究函数 y=2|x-2|-1 的图象与性质:当x≥2时,y=2|x-2|-1=2x-5,当x<2时,y=2|x-2|-1=-2x+3;
①列表:
x … -1 0 1 2 3 4 5 …
y … 5 3 1 -1 1 3 5 …
②请根据①中表格里的数据在给出的平面直角坐标系中描点,并画出y=2|x-2|-1的图象.
③多选题:结合图象,下列说法正确的有 ________ .
A.函数最小值是-1
B.x>2时,y值随x值的增大而增大
C.当x≤ 或x≥ 时,y≥0
D.当1<x≤4时,1<y≤3
(2)【拓展应用】若关于x的方程2|x-2|-1= x+m有两个均大于1的实数解,结合图象直接写出m的取值范围.
A,B,C
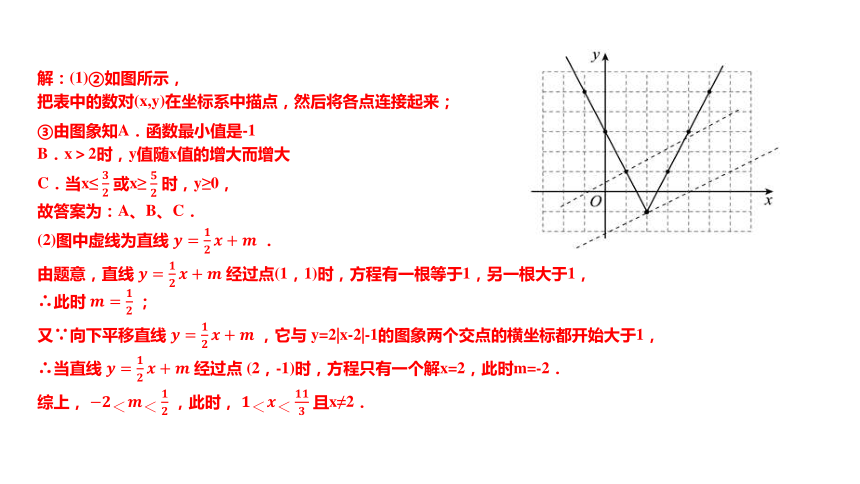
解:(1)②如图所示,
把表中的数对(x,y)在坐标系中描点,然后将各点连接起来;
___
③由图象知A.函数最小值是-1
B.x>2时,y值随x值的增大而增大
C.当x≤ 或x≥ 时,y≥0,
故答案为:A、B、C.
(2)图中虚线为直线 .
由题意,直线 经过点(1,1)时,方程有一根等于1,另一根大于1,
∴此时 ;
又∵向下平移直线 ,它与 y=2|x-2|-1的图象两个交点的横坐标都开始大于1,
∴当直线 经过点 (2,-1)时,方程只有一个解x=2,此时m=-2.
综上, ,此时, 且x≠2.
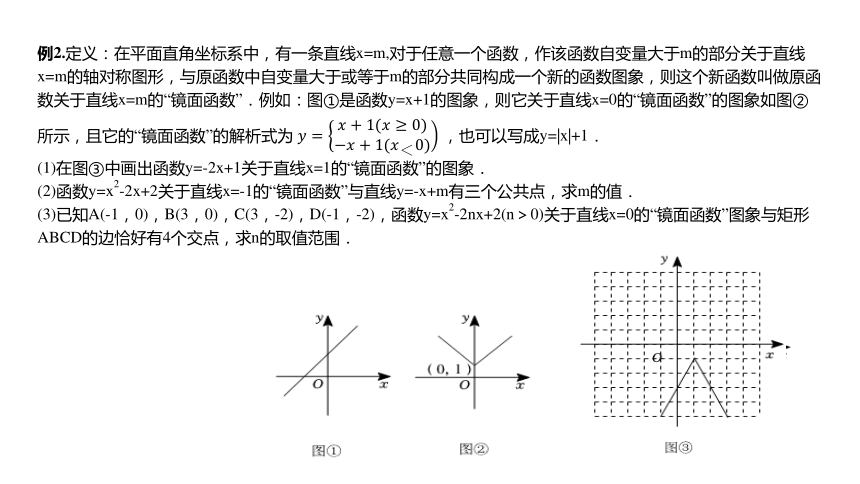
例2.定义:在平面直角坐标系中,有一条直线x=m,对于任意一个函数,作该函数自变量大于m的部分关于直线x=m的轴对称图形,与原函数中自变量大于或等于m的部分共同构成一个新的函数图象,则这个新函数叫做原函数关于直线x=m的“镜面函数”.例如:图①是函数y=x+1的图象,则它关于直线x=0的“镜面函数”的图象如图②所示,且它的“镜面函数”的解析式为 ,也可以写成y=|x|+1.
______
(1)在图③中画出函数y=-2x+1关于直线x=1的“镜面函数”的图象.
(2)函数y=x2-2x+2关于直线x=-1的“镜面函数”与直线y=-x+m有三个公共点,求m的值.
(3)已知A(-1,0),B(3,0),C(3,-2),D(-1,-2),函数y=x2-2nx+2(n>0)关于直线x=0的“镜面函数”图象与矩形ABCD的边恰好有4个交点,求n的取值范围.
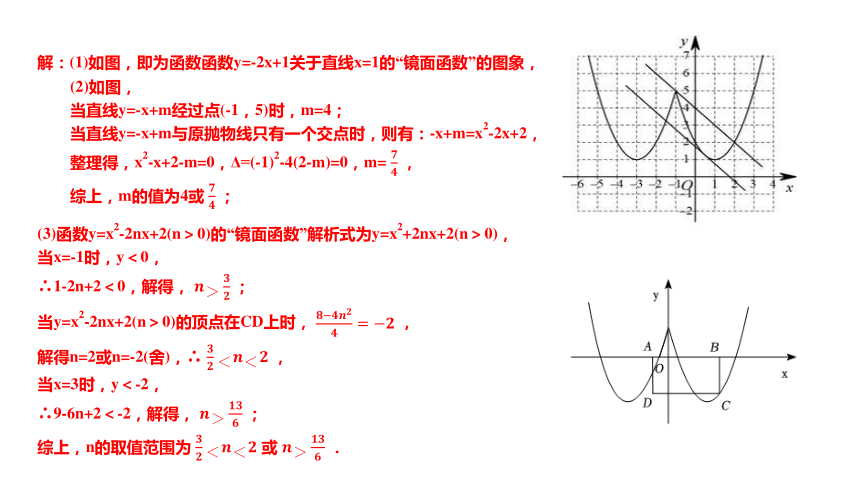
解:(1)如图,即为函数函数y=-2x+1关于直线x=1的“镜面函数”的图象,
_____
(2)如图,
当直线y=-x+m经过点(-1,5)时,m=4;
当直线y=-x+m与原抛物线只有一个交点时,则有:-x+m=x2-2x+2,
整理得,x2-x+2-m=0,Δ=(-1)2-4(2-m)=0,m= ,
综上,m的值为4或 ;
(3)函数y=x2-2nx+2(n>0)的“镜面函数”解析式为y=x2+2nx+2(n>0),
当x=-1时,y<0,
∴1-2n+2<0,解得, ;
当y=x2-2nx+2(n>0)的顶点在CD上时, ,
解得n=2或n=-2(舍),∴ ,
当x=3时,y<-2,
∴9-6n+2<-2,解得, ;
综上,n的取值范围为 或 .
例3.小云在学习过程中遇到一个函数 (x≥-2).下面是小云对其探究的过程,请补充完整:
(1)当-2≤x<0时,对于函数y1=|x|,即y1=-x,当-2≤x<0时,y1随x的增大而 ,且y1>0;对于函数y2=x2-x+1,-2≤x<0当时,y2随x的增大而 ,且y2>0;结合上述分析,进一步探究发现,对于函数y,当-2≤x<0时,y随x的增大而 .
(2)当x≥0时,对于函数y,当x≥0时,y与x的几组对应值如下表:
x 0 1 2 3
y 0 1
综合上表,进一步探究发现,当x≥0时,y随x的增大而增大.在平面直角坐标系xOy中,画出当x≥0时的函数y的图象.
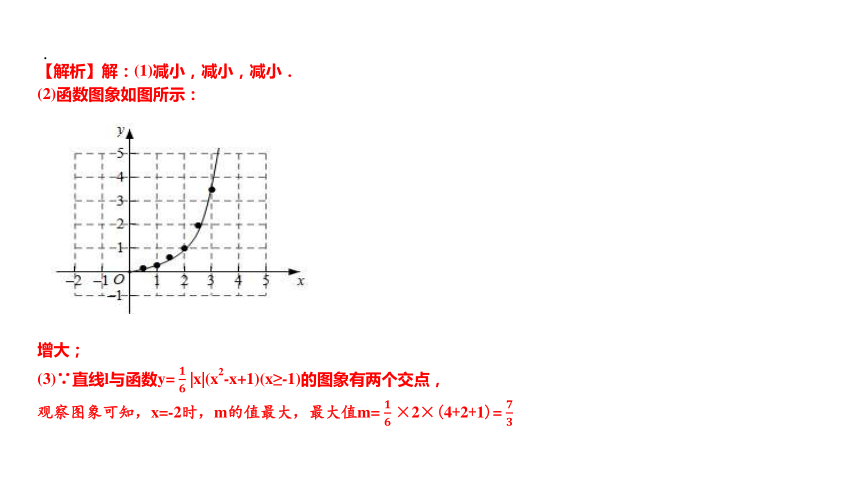
(3)过点(0,m)(m>0)作平行于x轴的直线l,结合(1)(2)的分析,解决问题:若直线l与函数 的图象有两个交点,则m的最大值是 .
.
【解析】解:(1)减小,减小,减小.
(2)函数图象如图所示:
增大;
(3)∵直线l与函数y= |x|(x2-x+1)(x≥-1)的图象有两个交点,
观察图象可知,x=-2时,m的值最大,最大值m= ×2×(4+2+1)=
例4:有这样一个问题:探究函数y= x2+ 的图象与性质,小东根据学习函数的经验,对函数y= x2+ 的图象与性质进行了探究,下面是小东的探究过程,请补充完整:
(1)下表是y与x的几组对应值.
x … -3 -2 -1 1 2 3 …
y … - m …
函数y= x2+ 的自变量x的取值范围是 ,m的值为 ;
(2)在如图所示的平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点.并画出该函数的大致图象;
(3)进一步探究函数图象发现:
①函数图象与x轴有 个交点,所以对应方程 x2+ =0有 个实数根;
②方程 x2+ =2有 个实数根;
③结合函数的图象,写出该函数的一条性质 .
解:(1)x≠0, .
(2)函数图象如图所示.
(3)①1,1.
②3.
③函数没有最大值或这个函数没有最小值,函数图象没有经过第四象限
_
1.作一条线段等于已知线段:
2.作已知角的平分线:
3.作已知线段的垂直平1.作一条线段等于已知线段:
2.作已知角的平分线:
3.作已知线段的垂直平分线:
4.作一个角等于已知角:
5.过一点作已知直线的垂线【点在线上、点在线外】。分线:
4.作一个角等于已知角:
5.过一点作已知直线的垂线【点在线上、点在线外】。
模块二:函数与综合探究
例1. 在综合实践课上,数学探究小组用两个互相垂直的直尺制作了一个“T”形尺,并用它对二次函数图象的相关性质进行研究.
把“T”形尺按图1摆放,水平宽AB的中点为C,图象的顶点为D,测得AB为m厘米时,CD为n厘米.
【猜想】
(1)探究小组先对y=x2的图象进行多次测量,测得m与n的部分数据如表:
m 0 2 3 4 5 6 …
n 0 1 2.25 4 6.25 9 …
描点:以表中各组对应值为点的坐标,在图2的直角坐标系内描出相应的点.
连线:用光滑的曲线顺次连接各点.
猜想:n与m的关系式是
【验证】
(2)探究小组又对多个二次函数的图象进行了测量研究,
发现测得的n与m也存在类似的关系式,并针对二次函数
y=a(x-h)2+k(a>0)的情况进行了推理验证.请从下表中任
选一种方法(在“□”内打“√”)并补全其推理过程;(根据需要,选用字母a,m,n,h,k表示答案)
□方法1 □方法2
___ 如图3,平移二次函数图象,使得顶点D移到原点O的位置,则: A'B'=AB=m,C'O=CD=n, C'B= , 所以点B′坐标为 ; 将点B′坐标代入y=ax2, 得到n与m的关系式是 . ___
如图4,顶点D的横坐标加 个单位,纵坐标加n个单位得到点B的坐标,所以点B坐标为 ;
将点B坐标代入y=a(x-h)2+k,
得到n与m的关系式是 .
【应用】
(3)已知AB∥x轴且AB=4,两个二次函数y=2(x-h)2+k和y=a(x-h)2+d的图象都经过A,B两点.当两个函数图象的顶点之间的距离为10时,求a的值.
___
【解析】解:(1)描点连线绘制函数图象如下:
点B( m,n),,将点B的坐标代入-:n=( m)2= m2;
故答案为:n= m2;
(2)方案一:( m,n),n= am2;
方案二:(h+ m,k+n),n= am2;
(3)①当a>0时,此时抛物线开口方向向上,
由(2)知a= ,n= ,
∵y=2(x-n)2+k,
∴n1= =8,
∵两个函数图象的顶点之间的距离为10,
∴n2=18,
∴a= = ;
②当a<0时,同理可得:n2=-2,此时a=-
综上,a= 或- .
例2. 乒乓球被誉为中国国球.2023年的世界乒乓球锦标赛中,中国队包揽了五个项目的冠军,成绩的取得与平时的刻苦训练和精准的技术分析是分不开的.如图,是乒乓球台的截面示意图,一位运动员从球台边缘正上方以击球高度OA为28.75cm的高度,将乒乓球向正前方击打到对面球台,乒乓球的运行路线近似是抛物线的一部分.
乒乓球到球台的竖直高度记为y(单位:cm),乒乓球运行的水平距离记为x(单位:cm).测得如下数据:
水平距离x/cm 0 10 50 90 130 170 230
竖直高度y/cm 28.75 33 45 49 45 33 0
(1)在平面直角坐标系xOy中,描出图③表格中各组数值所对应的点(x,y),并画出表示乒乓球运行轨迹形状的大致图象;
(2)①当乒乓球到达最高点时,与球台之间的距离是 ____ cm,当乒乓球落在对面球台上时,到起始点的水平距离是 _____ cm;
49
230
②求满足条件的抛物线解析式;
(3)技术分析:如果只上下调整击球高度OA,乒乓球的运行轨迹形状不变,那么为了确保乒乓球既能过网,又能落在对面球台上,需要计算出OA的取值范围,以利于有针对性的训练,如图②.乒乓球台长OB为274cm,球网高CD为15.25cm.现在已经计算出乒乓球恰好过网的击球高度OA的值约为1.27cm.请你计算出乒乓球恰好落在对面球台边缘点B处时,击球高度OA的值(乒乓球大小忽略不计).
【解析】解:(1)如图所示,
(2)49;230;
②设抛物线解析式为y=a(x-90)2+49,将(230,0)代入得,
0=a(230-90)2+49,
解得:a=-0.0025,
∴抛物线解析式为y=-0.0025(x-90)2+49;
(3)设乒乓球恰好落在对面球台边缘点B处时,击球高度OA的值为h,则平移距离为h-28.75(cm),
∴平移后的抛物线的解析式为y=-0.0025(x-90)2+49+h-28.75,
依题意,当x=274时,y=0,
∴-0.0025(274-90)2+49+h-28.75=0,
解得:h=64.39;
答:乒乓球恰好落在对面球台边缘点B处时,击球高度OA的值为64.39cm.
针对训练【项目式学习】
项目主题:安全用电,防患未然.
项目背景:近年来,随着电动自行车保有量不断增多,火灾风险持续上升.据悉,约80%的火灾都在充电时发生.某校九年级数学创新小组,开展以“安全用电,防患未然”为主题的项目式学习,对电动自行车充电车棚的消防设备进行研究.
任务一:调查分析
(1)图1悬挂的是8公斤干粉灭火器,图2为其喷射截面示意图,在△AOB中,OA=OB,喷射角∠AOB=60°,地面有效保护直径AB为 米,喷嘴O距离地面的高度OC为 米;
任务二;模型构建
由于干粉灭火器只能扑灭明火,并不能扑灭电池内部的燃烧,在火灾发生时需要大量的水持续给电池降温,才能保证电池内部自燃熄灭,不会复燃.学校考虑给新建的电动自行车充电车棚安装消防喷淋头.
(2)如图3,喷淋头喷洒的水柱最外层的形状为抛物线.已知学校的停车棚左侧靠墙建造,其截面示意图为矩形OABC,创新小组以点O为坐标原点,墙面OA所在直线为y轴,建立如图4所示的平面直角坐标系.他们查阅资料后,提议消防喷淋头M安装在离地高度为3米,距离墙面水平距离为2米处,即OA=3米,AM=2米,水喷射到墙面D处,且OD=1米.
①求该水柱外层所在抛物线的函数解析式;②按照此安装方式,喷淋头M的地面有效保护直径OE为 米;
任务三:问题解决
(3)已知充电车棚宽度OC为7米,电动车电池的离地高度为0.2米.创新小组想在喷淋头M的同一水平线AB上加装一个喷淋头N,使消防喷淋头喷洒的水柱可以覆盖所有电动车电池,喷淋头N距离喷淋头M至少 米.
____
【解析】解:3;
任务二:(2)①由题意得:点M(2,3)为抛物线的顶点坐标.
∴设抛物线的解析式为:y=a(x-2)2+3(a≠0).
∵经过点(0,1),
∴1=a(0-2)2+3.
解得:a=- .
∴该水柱外层所在抛物线的函数解析式为:y=- (x-2)2+3.
②2+ ;
任务三:(3)由题意得:喷淋头N在喷淋头M右边,设距离喷淋头M有b米.
∴水柱外层所在抛物线的函数抛物线解析式为:y=- (x-2-b)2+3.
∵经过点(7,0.2),
∴- (7-2-b)2+3=0.2.
(5-b)2=5.6.
5-b=± .
∴b1=5+ (超过7米,舍去),b2=5- .
故答案为:5- .
1.作一条线段等于已知线段:
2.作已知角的平分线:
3.作已知线段的垂直平1.作一条线段等于已知线段:
2.作已知角的平分线:
3.作已知线段的垂直平分线:
4.作一个角等于已知角:
5.过一点作已知直线的垂线【点在线上、点在线外】。分线:
4.作一个角等于已知角:
5.过一点作已知直线的垂线【点在线上、点在线外】。
模块三:函数与新定义
13.【概念学习】
在平面直角坐标系中,点M的坐标为(x1,y1),若图形F上存在一点N(x2,y2),且满足当x1=x2时,MN≤2,则称点M为图形F的一个“垂近点”.
【初步理解】
(1)如图1,图形F为线段AB,点A(-1,2),B(3,2).
①试判断点M(1.5,0) ____ (填“是”或“不是”)线段AB的“垂近点”.
②请在图中画出点M所有可能的位置.(用阴影部分表示)
【知识应用】
(2)若图形F为直线y=b,二次函数y=ax2+2ax+a-
图象上仅有一个“垂近点”,求b的值.
(3)如图2,若图形F为抛物线y= -4,正方形ABCD的边长为2,
中心(对角线的交点)为P(a,0),如果正方形ABCD上存在“垂近点”,
求出a的取值范围.
是
【解析】解:(1)①当x=1.5时,|2-0|=2≤2,
∴点M(1.5,0)是线段AB的“垂近点”,
故答案为:是;
②M所有可能的位置,如图所示,
(2)将y=ax2+2ax+a- 化成顶点式,y=a(x+1)2- ,
当a<0时,b=- ,
当a>0时,b=- ,
∴b= 或b=- ,
(3)∵点P(a,0)是正方形的中心,正方形的边长为2,
∴A(a-1,-1),B(a+1,-1),C(a+1,1),D(a-1,1),
设正方形上点M是抛物线y= -4的“垂近点”,抛物线上存在点N(xN,yN),使得当xM=xN时,MN≤2,
当点P在y轴右侧时,a>0,
如图2,当点M与点D重合时, ,
∴MN= -4-1=2,
解得:a=1+2 或a=1-2 (不合题意,舍去),
如图3,当点M与点B重合时, ,
∴MN=-1- +4=2,
解得:a=1或a=-3(舍),
当点P在y轴左侧时,a<0,
如图4,当点M与点C重合时, ,
∴MN= -4-1=2,
解得:a=-1-2 或a=-1+2 (舍),
如图4,当点M与点A重合时, ,
∴MN=-1- +4=2,
解得:a=-1或a=3(舍),
∴当1≤a≤1+2 或-1-2 ≤a≤-1时,正方形上存在抛物线y= -4的“垂近点”.
___
14.定义:若一个函数图象上存在坐标轴距离相等的点,则称该点为这个函数图象的“等距点”.例如,点(1,1)和 是函数图象y= 的“等距点”.
(1)判断函数y=x2+2x的图象是否存在“等距点“?如果存在,求出“等距点”的坐标;如果不存在,说明理由;
(2)设函数y=- 图象的“等距点”为A、B,函数y=-x+b图象的“等距点”为C,若△ABC的面积为2 时,请直接写出满足条件的函数y=-x+b的表达式;
(3)若函数y=-x2+2x+2m+2 图象只存在2个“等距点”,试求出m的取值范围.
【解析】解:(1)存在“等距点”,
令x2+2x=x,
解得x1=0,x2=-1,
∴函数y=x2+2x的图象上有两个“等距点”(0,0)或(-1,-1),
令x2+2x=-x,
解得x1=0,x2=-3,
∴函数y=x2+2x的图象上有两个“等距点”(0,0)或(-3,3),
综上,有三个“等距点”(0,0)或(-1,-1)或(-3,3);
(2)令- =-x,
解得x1=-2,x2=2,
则A(-2,2),B(2,-2),
∴AB=4 ,
令-x+b=x,
解得:x= ,
则点C( , ),
∴CO= |b|,
∵AB⊥OC,
∴S△ABC= AB CO,
即2 = ×4 × |b|,
解得:b=± ,
则y=-x± ;
此外,当b=0 任意C都为等距点,
故:y=-x,
综上,y=-x± 或y=-x;
(3)令x=-x2+2x+2m+2,
整理得:x2-x-2m-2=0,
Δ=1+4(2m+2)=8m+9,
当m>- 时,Δ>0,
此时在一、三象限有2个“等距点”.
令-x=-x2+2x+2m+2,
整理得,x2-3x-2m-2=0,
则Δ=32+4(2m+2)=8m+17,
则当m>- 时,Δ>0,
此时在二四象限有2个“等距点”.
∵函数y=-x2+(2+m)x+2m+2图象恰存在2个“等距点”,
综上,- <m<- .
祝初三学子中考必胜!
第13讲 新函数图像探究题
罗湖区中考备考“百师助学”课程
深圳市桂园中学 郭培香
中线等分三角形面积
一、知识要点
新函数图像探究题是近些年中考数学的一种新题型,在北京、河南、重庆等地的中考数学试卷中已有出现,近年来越来越频繁地出现在深圳的中考数学试卷中。
新函数图像探究题是建立在学生已经学习的一次函数、反比例函数和二次函数基础之上,将基本函数进行组合、变形、平移等形成新的函数,是对函数图像与性质的综合运用。
在初中阶段的函数学习中,我们经历了“确定函数的表达式﹣﹣利用函数图象研究其性质一一运用函数解决问题”的学习过程.新函数图像的探究题的学习也是同样的过程,作出函数图像是解题的关键。
中线等分三角形面积
一、知识要点
函数图象性质的探究题常见问题:
①求变量的取值范围:根据解析式中分式、二次根式等有意义的条件,列出不等式(组)进行求解;
②描点、连线画函数图象:用平滑的曲线依次连接各点即可;
③写函数的相关性质:根据函数图象,从最值、增减性、对称性、特殊点等方面入手即可;
④函数与方程或不等式综合考查,观察函数图像求值或取值范围,理解函数图像的交点的坐标与方程的解的关系,掌握在同一坐标系中不同函数的值的大小与函数图像的位置关系是解题的关键;
⑤函数与几何综合、函数与实践探究及新定义的考查。
1.作一条线段等于已知线段:
2.作已知角的平分线:
3.作已知线段的垂直平1.作一条线段等于已知线段:
2.作已知角的平分线:
3.作已知线段的垂直平分线:
4.作一个角等于已知角:
5.过一点作已知直线的垂线【点在线上、点在线外】。分线:
4.作一个角等于已知角:
5.过一点作已知直线的垂线【点在线上、点在线外】。
模块一:新函数的四种常见类型
一、绝对值函数
二、分段函数
三、高次函数
四、组合函数
例1.学完一次函数后,小明同学通过列表、描点、连线的方法画函数图象,并利用函数图象研究函数的性质,由于在七年级学习了绝对值的意义: ,请你帮助小明完成下列问题.
(1)【探索】探究函数 y=2|x-2|-1 的图象与性质:当x≥2时,y=2|x-2|-1=2x-5,当x<2时,y=2|x-2|-1=-2x+3;
①列表:
x … -1 0 1 2 3 4 5 …
y … 5 3 1 -1 1 3 5 …
②请根据①中表格里的数据在给出的平面直角坐标系中描点,并画出y=2|x-2|-1的图象.
③多选题:结合图象,下列说法正确的有 ________ .
A.函数最小值是-1
B.x>2时,y值随x值的增大而增大
C.当x≤ 或x≥ 时,y≥0
D.当1<x≤4时,1<y≤3
(2)【拓展应用】若关于x的方程2|x-2|-1= x+m有两个均大于1的实数解,结合图象直接写出m的取值范围.
A,B,C
解:(1)②如图所示,
把表中的数对(x,y)在坐标系中描点,然后将各点连接起来;
___
③由图象知A.函数最小值是-1
B.x>2时,y值随x值的增大而增大
C.当x≤ 或x≥ 时,y≥0,
故答案为:A、B、C.
(2)图中虚线为直线 .
由题意,直线 经过点(1,1)时,方程有一根等于1,另一根大于1,
∴此时 ;
又∵向下平移直线 ,它与 y=2|x-2|-1的图象两个交点的横坐标都开始大于1,
∴当直线 经过点 (2,-1)时,方程只有一个解x=2,此时m=-2.
综上, ,此时, 且x≠2.
例2.定义:在平面直角坐标系中,有一条直线x=m,对于任意一个函数,作该函数自变量大于m的部分关于直线x=m的轴对称图形,与原函数中自变量大于或等于m的部分共同构成一个新的函数图象,则这个新函数叫做原函数关于直线x=m的“镜面函数”.例如:图①是函数y=x+1的图象,则它关于直线x=0的“镜面函数”的图象如图②所示,且它的“镜面函数”的解析式为 ,也可以写成y=|x|+1.
______
(1)在图③中画出函数y=-2x+1关于直线x=1的“镜面函数”的图象.
(2)函数y=x2-2x+2关于直线x=-1的“镜面函数”与直线y=-x+m有三个公共点,求m的值.
(3)已知A(-1,0),B(3,0),C(3,-2),D(-1,-2),函数y=x2-2nx+2(n>0)关于直线x=0的“镜面函数”图象与矩形ABCD的边恰好有4个交点,求n的取值范围.
解:(1)如图,即为函数函数y=-2x+1关于直线x=1的“镜面函数”的图象,
_____
(2)如图,
当直线y=-x+m经过点(-1,5)时,m=4;
当直线y=-x+m与原抛物线只有一个交点时,则有:-x+m=x2-2x+2,
整理得,x2-x+2-m=0,Δ=(-1)2-4(2-m)=0,m= ,
综上,m的值为4或 ;
(3)函数y=x2-2nx+2(n>0)的“镜面函数”解析式为y=x2+2nx+2(n>0),
当x=-1时,y<0,
∴1-2n+2<0,解得, ;
当y=x2-2nx+2(n>0)的顶点在CD上时, ,
解得n=2或n=-2(舍),∴ ,
当x=3时,y<-2,
∴9-6n+2<-2,解得, ;
综上,n的取值范围为 或 .
例3.小云在学习过程中遇到一个函数 (x≥-2).下面是小云对其探究的过程,请补充完整:
(1)当-2≤x<0时,对于函数y1=|x|,即y1=-x,当-2≤x<0时,y1随x的增大而 ,且y1>0;对于函数y2=x2-x+1,-2≤x<0当时,y2随x的增大而 ,且y2>0;结合上述分析,进一步探究发现,对于函数y,当-2≤x<0时,y随x的增大而 .
(2)当x≥0时,对于函数y,当x≥0时,y与x的几组对应值如下表:
x 0 1 2 3
y 0 1
综合上表,进一步探究发现,当x≥0时,y随x的增大而增大.在平面直角坐标系xOy中,画出当x≥0时的函数y的图象.
(3)过点(0,m)(m>0)作平行于x轴的直线l,结合(1)(2)的分析,解决问题:若直线l与函数 的图象有两个交点,则m的最大值是 .
.
【解析】解:(1)减小,减小,减小.
(2)函数图象如图所示:
增大;
(3)∵直线l与函数y= |x|(x2-x+1)(x≥-1)的图象有两个交点,
观察图象可知,x=-2时,m的值最大,最大值m= ×2×(4+2+1)=
例4:有这样一个问题:探究函数y= x2+ 的图象与性质,小东根据学习函数的经验,对函数y= x2+ 的图象与性质进行了探究,下面是小东的探究过程,请补充完整:
(1)下表是y与x的几组对应值.
x … -3 -2 -1 1 2 3 …
y … - m …
函数y= x2+ 的自变量x的取值范围是 ,m的值为 ;
(2)在如图所示的平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点.并画出该函数的大致图象;
(3)进一步探究函数图象发现:
①函数图象与x轴有 个交点,所以对应方程 x2+ =0有 个实数根;
②方程 x2+ =2有 个实数根;
③结合函数的图象,写出该函数的一条性质 .
解:(1)x≠0, .
(2)函数图象如图所示.
(3)①1,1.
②3.
③函数没有最大值或这个函数没有最小值,函数图象没有经过第四象限
_
1.作一条线段等于已知线段:
2.作已知角的平分线:
3.作已知线段的垂直平1.作一条线段等于已知线段:
2.作已知角的平分线:
3.作已知线段的垂直平分线:
4.作一个角等于已知角:
5.过一点作已知直线的垂线【点在线上、点在线外】。分线:
4.作一个角等于已知角:
5.过一点作已知直线的垂线【点在线上、点在线外】。
模块二:函数与综合探究
例1. 在综合实践课上,数学探究小组用两个互相垂直的直尺制作了一个“T”形尺,并用它对二次函数图象的相关性质进行研究.
把“T”形尺按图1摆放,水平宽AB的中点为C,图象的顶点为D,测得AB为m厘米时,CD为n厘米.
【猜想】
(1)探究小组先对y=x2的图象进行多次测量,测得m与n的部分数据如表:
m 0 2 3 4 5 6 …
n 0 1 2.25 4 6.25 9 …
描点:以表中各组对应值为点的坐标,在图2的直角坐标系内描出相应的点.
连线:用光滑的曲线顺次连接各点.
猜想:n与m的关系式是
【验证】
(2)探究小组又对多个二次函数的图象进行了测量研究,
发现测得的n与m也存在类似的关系式,并针对二次函数
y=a(x-h)2+k(a>0)的情况进行了推理验证.请从下表中任
选一种方法(在“□”内打“√”)并补全其推理过程;(根据需要,选用字母a,m,n,h,k表示答案)
□方法1 □方法2
___ 如图3,平移二次函数图象,使得顶点D移到原点O的位置,则: A'B'=AB=m,C'O=CD=n, C'B= , 所以点B′坐标为 ; 将点B′坐标代入y=ax2, 得到n与m的关系式是 . ___
如图4,顶点D的横坐标加 个单位,纵坐标加n个单位得到点B的坐标,所以点B坐标为 ;
将点B坐标代入y=a(x-h)2+k,
得到n与m的关系式是 .
【应用】
(3)已知AB∥x轴且AB=4,两个二次函数y=2(x-h)2+k和y=a(x-h)2+d的图象都经过A,B两点.当两个函数图象的顶点之间的距离为10时,求a的值.
___
【解析】解:(1)描点连线绘制函数图象如下:
点B( m,n),,将点B的坐标代入-:n=( m)2= m2;
故答案为:n= m2;
(2)方案一:( m,n),n= am2;
方案二:(h+ m,k+n),n= am2;
(3)①当a>0时,此时抛物线开口方向向上,
由(2)知a= ,n= ,
∵y=2(x-n)2+k,
∴n1= =8,
∵两个函数图象的顶点之间的距离为10,
∴n2=18,
∴a= = ;
②当a<0时,同理可得:n2=-2,此时a=-
综上,a= 或- .
例2. 乒乓球被誉为中国国球.2023年的世界乒乓球锦标赛中,中国队包揽了五个项目的冠军,成绩的取得与平时的刻苦训练和精准的技术分析是分不开的.如图,是乒乓球台的截面示意图,一位运动员从球台边缘正上方以击球高度OA为28.75cm的高度,将乒乓球向正前方击打到对面球台,乒乓球的运行路线近似是抛物线的一部分.
乒乓球到球台的竖直高度记为y(单位:cm),乒乓球运行的水平距离记为x(单位:cm).测得如下数据:
水平距离x/cm 0 10 50 90 130 170 230
竖直高度y/cm 28.75 33 45 49 45 33 0
(1)在平面直角坐标系xOy中,描出图③表格中各组数值所对应的点(x,y),并画出表示乒乓球运行轨迹形状的大致图象;
(2)①当乒乓球到达最高点时,与球台之间的距离是 ____ cm,当乒乓球落在对面球台上时,到起始点的水平距离是 _____ cm;
49
230
②求满足条件的抛物线解析式;
(3)技术分析:如果只上下调整击球高度OA,乒乓球的运行轨迹形状不变,那么为了确保乒乓球既能过网,又能落在对面球台上,需要计算出OA的取值范围,以利于有针对性的训练,如图②.乒乓球台长OB为274cm,球网高CD为15.25cm.现在已经计算出乒乓球恰好过网的击球高度OA的值约为1.27cm.请你计算出乒乓球恰好落在对面球台边缘点B处时,击球高度OA的值(乒乓球大小忽略不计).
【解析】解:(1)如图所示,
(2)49;230;
②设抛物线解析式为y=a(x-90)2+49,将(230,0)代入得,
0=a(230-90)2+49,
解得:a=-0.0025,
∴抛物线解析式为y=-0.0025(x-90)2+49;
(3)设乒乓球恰好落在对面球台边缘点B处时,击球高度OA的值为h,则平移距离为h-28.75(cm),
∴平移后的抛物线的解析式为y=-0.0025(x-90)2+49+h-28.75,
依题意,当x=274时,y=0,
∴-0.0025(274-90)2+49+h-28.75=0,
解得:h=64.39;
答:乒乓球恰好落在对面球台边缘点B处时,击球高度OA的值为64.39cm.
针对训练【项目式学习】
项目主题:安全用电,防患未然.
项目背景:近年来,随着电动自行车保有量不断增多,火灾风险持续上升.据悉,约80%的火灾都在充电时发生.某校九年级数学创新小组,开展以“安全用电,防患未然”为主题的项目式学习,对电动自行车充电车棚的消防设备进行研究.
任务一:调查分析
(1)图1悬挂的是8公斤干粉灭火器,图2为其喷射截面示意图,在△AOB中,OA=OB,喷射角∠AOB=60°,地面有效保护直径AB为 米,喷嘴O距离地面的高度OC为 米;
任务二;模型构建
由于干粉灭火器只能扑灭明火,并不能扑灭电池内部的燃烧,在火灾发生时需要大量的水持续给电池降温,才能保证电池内部自燃熄灭,不会复燃.学校考虑给新建的电动自行车充电车棚安装消防喷淋头.
(2)如图3,喷淋头喷洒的水柱最外层的形状为抛物线.已知学校的停车棚左侧靠墙建造,其截面示意图为矩形OABC,创新小组以点O为坐标原点,墙面OA所在直线为y轴,建立如图4所示的平面直角坐标系.他们查阅资料后,提议消防喷淋头M安装在离地高度为3米,距离墙面水平距离为2米处,即OA=3米,AM=2米,水喷射到墙面D处,且OD=1米.
①求该水柱外层所在抛物线的函数解析式;②按照此安装方式,喷淋头M的地面有效保护直径OE为 米;
任务三:问题解决
(3)已知充电车棚宽度OC为7米,电动车电池的离地高度为0.2米.创新小组想在喷淋头M的同一水平线AB上加装一个喷淋头N,使消防喷淋头喷洒的水柱可以覆盖所有电动车电池,喷淋头N距离喷淋头M至少 米.
____
【解析】解:3;
任务二:(2)①由题意得:点M(2,3)为抛物线的顶点坐标.
∴设抛物线的解析式为:y=a(x-2)2+3(a≠0).
∵经过点(0,1),
∴1=a(0-2)2+3.
解得:a=- .
∴该水柱外层所在抛物线的函数解析式为:y=- (x-2)2+3.
②2+ ;
任务三:(3)由题意得:喷淋头N在喷淋头M右边,设距离喷淋头M有b米.
∴水柱外层所在抛物线的函数抛物线解析式为:y=- (x-2-b)2+3.
∵经过点(7,0.2),
∴- (7-2-b)2+3=0.2.
(5-b)2=5.6.
5-b=± .
∴b1=5+ (超过7米,舍去),b2=5- .
故答案为:5- .
1.作一条线段等于已知线段:
2.作已知角的平分线:
3.作已知线段的垂直平1.作一条线段等于已知线段:
2.作已知角的平分线:
3.作已知线段的垂直平分线:
4.作一个角等于已知角:
5.过一点作已知直线的垂线【点在线上、点在线外】。分线:
4.作一个角等于已知角:
5.过一点作已知直线的垂线【点在线上、点在线外】。
模块三:函数与新定义
13.【概念学习】
在平面直角坐标系中,点M的坐标为(x1,y1),若图形F上存在一点N(x2,y2),且满足当x1=x2时,MN≤2,则称点M为图形F的一个“垂近点”.
【初步理解】
(1)如图1,图形F为线段AB,点A(-1,2),B(3,2).
①试判断点M(1.5,0) ____ (填“是”或“不是”)线段AB的“垂近点”.
②请在图中画出点M所有可能的位置.(用阴影部分表示)
【知识应用】
(2)若图形F为直线y=b,二次函数y=ax2+2ax+a-
图象上仅有一个“垂近点”,求b的值.
(3)如图2,若图形F为抛物线y= -4,正方形ABCD的边长为2,
中心(对角线的交点)为P(a,0),如果正方形ABCD上存在“垂近点”,
求出a的取值范围.
是
【解析】解:(1)①当x=1.5时,|2-0|=2≤2,
∴点M(1.5,0)是线段AB的“垂近点”,
故答案为:是;
②M所有可能的位置,如图所示,
(2)将y=ax2+2ax+a- 化成顶点式,y=a(x+1)2- ,
当a<0时,b=- ,
当a>0时,b=- ,
∴b= 或b=- ,
(3)∵点P(a,0)是正方形的中心,正方形的边长为2,
∴A(a-1,-1),B(a+1,-1),C(a+1,1),D(a-1,1),
设正方形上点M是抛物线y= -4的“垂近点”,抛物线上存在点N(xN,yN),使得当xM=xN时,MN≤2,
当点P在y轴右侧时,a>0,
如图2,当点M与点D重合时, ,
∴MN= -4-1=2,
解得:a=1+2 或a=1-2 (不合题意,舍去),
如图3,当点M与点B重合时, ,
∴MN=-1- +4=2,
解得:a=1或a=-3(舍),
当点P在y轴左侧时,a<0,
如图4,当点M与点C重合时, ,
∴MN= -4-1=2,
解得:a=-1-2 或a=-1+2 (舍),
如图4,当点M与点A重合时, ,
∴MN=-1- +4=2,
解得:a=-1或a=3(舍),
∴当1≤a≤1+2 或-1-2 ≤a≤-1时,正方形上存在抛物线y= -4的“垂近点”.
___
14.定义:若一个函数图象上存在坐标轴距离相等的点,则称该点为这个函数图象的“等距点”.例如,点(1,1)和 是函数图象y= 的“等距点”.
(1)判断函数y=x2+2x的图象是否存在“等距点“?如果存在,求出“等距点”的坐标;如果不存在,说明理由;
(2)设函数y=- 图象的“等距点”为A、B,函数y=-x+b图象的“等距点”为C,若△ABC的面积为2 时,请直接写出满足条件的函数y=-x+b的表达式;
(3)若函数y=-x2+2x+2m+2 图象只存在2个“等距点”,试求出m的取值范围.
【解析】解:(1)存在“等距点”,
令x2+2x=x,
解得x1=0,x2=-1,
∴函数y=x2+2x的图象上有两个“等距点”(0,0)或(-1,-1),
令x2+2x=-x,
解得x1=0,x2=-3,
∴函数y=x2+2x的图象上有两个“等距点”(0,0)或(-3,3),
综上,有三个“等距点”(0,0)或(-1,-1)或(-3,3);
(2)令- =-x,
解得x1=-2,x2=2,
则A(-2,2),B(2,-2),
∴AB=4 ,
令-x+b=x,
解得:x= ,
则点C( , ),
∴CO= |b|,
∵AB⊥OC,
∴S△ABC= AB CO,
即2 = ×4 × |b|,
解得:b=± ,
则y=-x± ;
此外,当b=0 任意C都为等距点,
故:y=-x,
综上,y=-x± 或y=-x;
(3)令x=-x2+2x+2m+2,
整理得:x2-x-2m-2=0,
Δ=1+4(2m+2)=8m+9,
当m>- 时,Δ>0,
此时在一、三象限有2个“等距点”.
令-x=-x2+2x+2m+2,
整理得,x2-3x-2m-2=0,
则Δ=32+4(2m+2)=8m+17,
则当m>- 时,Δ>0,
此时在二四象限有2个“等距点”.
∵函数y=-x2+(2+m)x+2m+2图象恰存在2个“等距点”,
综上,- <m<- .
祝初三学子中考必胜!
同课章节目录
