2025年深圳市中考备考百师助学培优课程——第14讲45度角解题策略 自主学习单(含答案)
文档属性
| 名称 | 2025年深圳市中考备考百师助学培优课程——第14讲45度角解题策略 自主学习单(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-05 18:03:19 | ||
图片预览


文档简介
自主学习单
一、前置学习
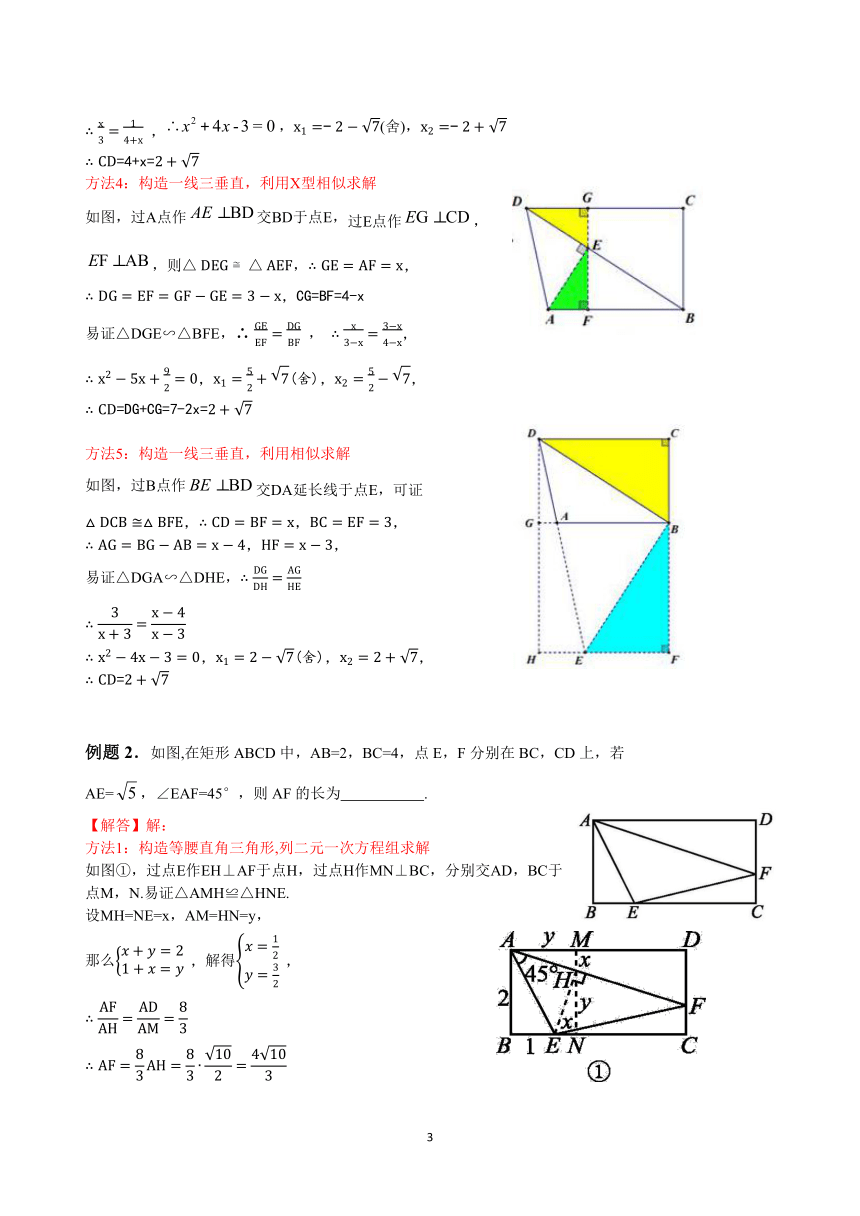
1、一线三等角
如图1,,,过点B作于点C,过点D作于点E.由,得.又,可以推理得到.进而得到DE,.我们把这个数学模型称为“K字”模型或“一线三等角”模型
2、正方形内半角模型
如图2,在正方形ABCD中,点E、F分别在边BC、CD上,∠EAF=45°,连接AE、AF、EF。则可将△ADF绕点A点顺时针旋转90°至△ABG处,使得AD和AB重合,即△ADF ≌△ABG,则有以下结论成立:
①△AEG ≌△AEF;
②BE+DF=EF;
③∠AEF=∠AEB,∠AFE=∠AFD;
图2 图3
3、方法归纳
(1)遇到45°→构造直角三角形→构造“一线三直角”
遇到45°→构造半角模型
遇到45°→构造圆心角为90度的圆
学习过程
模块一: 45度角问题初探
1、例题精讲
例题1.四边形 ABCD 中,AB∥CD,AB=4,BC=3,∠ABC=90°,∠ADB=45°.
求 CD 的长.
【解答】解:
方法1:构造一线三等角,利用相似求CD的长
如图,作,延长CD到点F,连接AF,使得∠CFA=45°,延长DC到点G,连接BG,使得∠BGD=45°,可证△ADF∽△DBG,,,在Rt△BCG中,,
△ADF∽△DBG
,即
,(舍),
方法2:构造直角三角形,构造母子型相似
如图,延长BA到点E,作
以E点为直角,作等腰直角三角形DEF,则△BAD∽△BDF,
, 设AE=x,BF=7+x,
在Rt△BED中,
,(舍),
=BE=4+x=
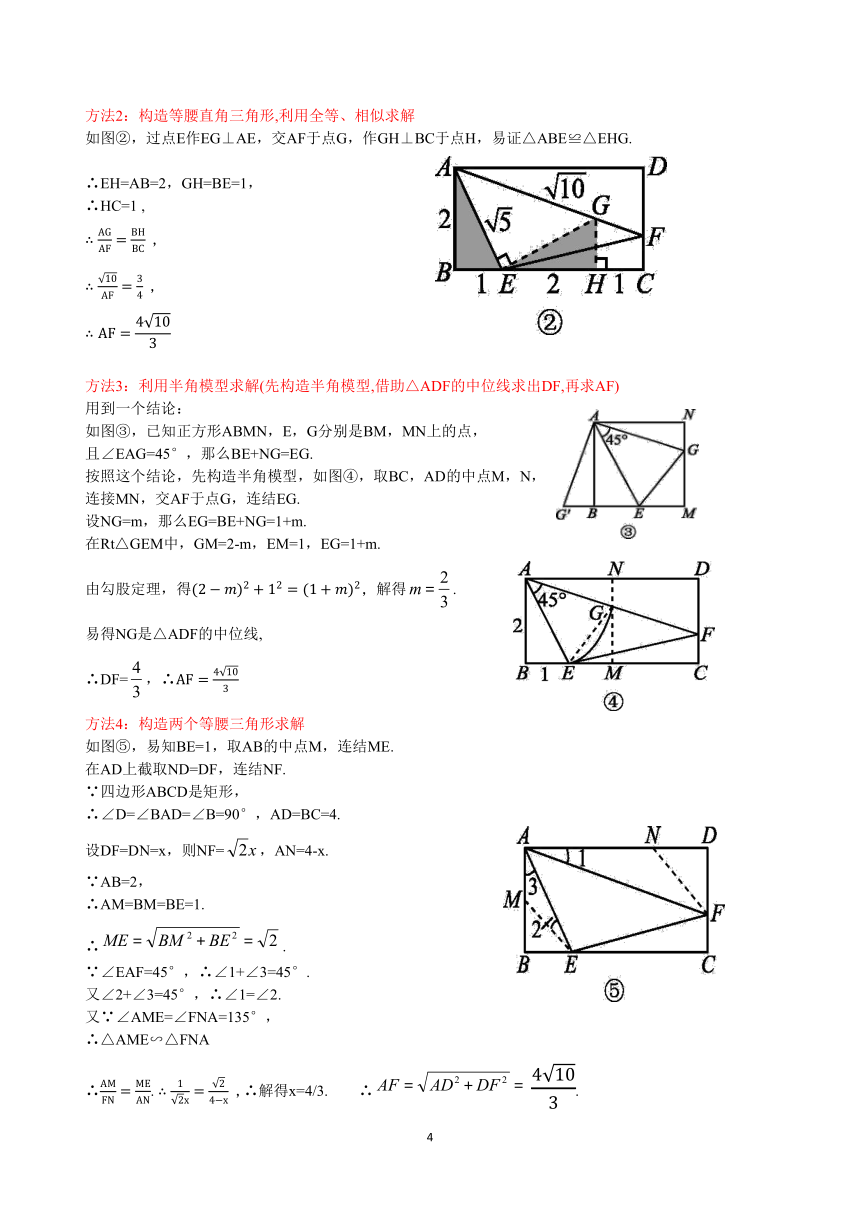
方法3:构造一线三垂直,利用A型相似求解
如图,延长BA到点F,作
过A点作交BD于点E,过E点作
则,
易证△EGB∽△DFB, ,设EG=x,
,,(舍),
=4+x=
方法4:构造一线三垂直,利用X型相似求解
如图,过A点作交BD于点E,过E点作,
,则,,
,CG=BF=4-x
易证△DGE∽△BFE, , ,
,(舍),,
=DG+CG=7-2x=
方法5:构造一线三垂直,利用相似求解
如图,过B点作交DA延长线于点E,可证
,,,
,
易证△DGA∽△DHE,
,(舍),,
=
例题2.如图,在矩形ABCD中,AB=2,BC=4,点E,F分别在BC,CD上,若
AE=,∠EAF=45°,则AF的长为 .
【解答】解:
方法1:构造等腰直角三角形,列二元一次方程组求解
如图①,过点E作EH⊥AF于点H,过点H作MN⊥BC,分别交AD,BC于点M,N.易证△AMH≌△HNE.
设MH=NE=x,AM=HN=y,
那么,解得 ,
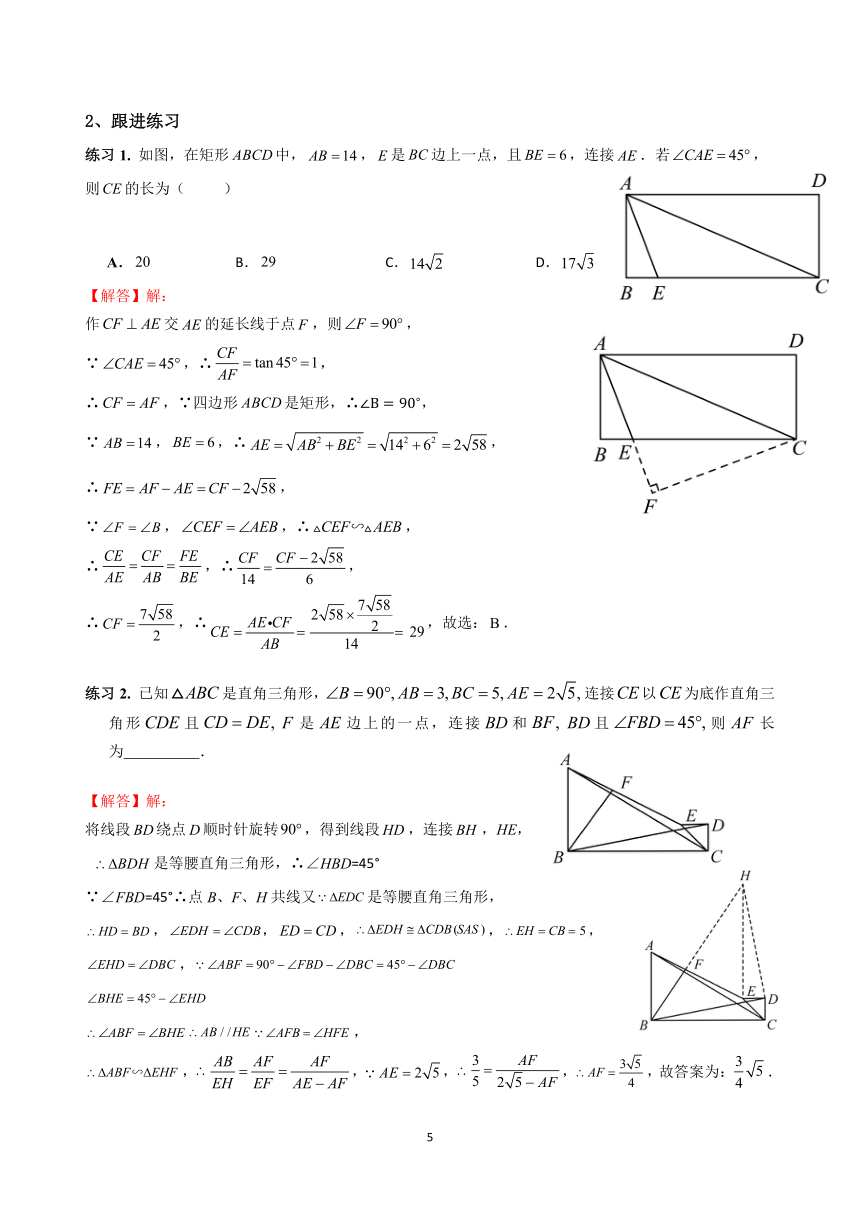
方法2:构造等腰直角三角形,利用全等、相似求解
如图②,过点E作EG⊥AE,交AF于点G,作GH⊥BC于点H,易证△ABE≌△EHG.
∴EH=AB=2,GH=BE=1,
∴HC=1 ,
,
,
方法3:利用半角模型求解(先构造半角模型,借助△ADF的中位线求出DF,再求AF)
用到一个结论:
如图③,已知正方形ABMN,E,G分别是BM,MN上的点,
且∠EAG=45°,那么BE+NG=EG.
按照这个结论,先构造半角模型,如图④,取BC,AD的中点M,N,
连接MN,交AF于点G,连结EG.
设NG=m,那么EG=BE+NG=1+m.
在Rt△GEM中,GM=2-m,EM=1,EG=1+m.
由勾股定理,得,解得.
易得NG是△ADF的中位线,
∴DF=,∴
方法4:构造两个等腰三角形求解
如图⑤,易知BE=1,取AB的中点M,连结ME.
在AD上截取ND=DF,连结NF.
∵四边形ABCD是矩形,
∴∠D=∠BAD=∠B=90°,AD=BC=4.
设DF=DN=x,则NF=,AN=4-x.
∵AB=2,
∴AM=BM=BE=1.
∴.
∵∠EAF=45°,∴∠1+∠3=45°.
又∠2+∠3=45°,∴∠1=∠2.
又∵∠AME=∠FNA=135°,
∴△AME∽△FNA
∴. ,∴解得x=4/3. ∴.
2、跟进练习
练习1. 如图,在矩形中,,是边上一点,且,连接.若,则的长为( )
B. C. D.
【解答】解:
作交的延长线于点,则,
∵,∴,
∴,∵四边形是矩形,∴,
∵,,∴,
∴,
∵,,∴,
∴,∴,
∴,∴,故选:.
练习2. 已知是直角三角形,连接以为底作直角三角形且是边上的一点,连接和且则长为 .
【解答】解:
将线段绕点顺时针旋转,得到线段,连接,HE,
是等腰直角三角形,∴∠HBD=45°
∵∠FBD=45°∴点B、F、H共线又是等腰直角三角形,
,,,,,,
,
,,,,,故答案为:.
练习3. 如图,△ABC为等腰直角三角形,,是上一点,交直线于点,且,,点为的中点,连接,则的长为( )
A. B. C. D.
【解答】解:如图,过点作交延长线于,
∵,∴, ∵,∴,
∴是等腰直角三角形, ∴,
设,则,由勾股定理得,,,
,∴,
整理得,
解得,(不合,舍去),
∴,∴,∵点为的中点,∴,故选:.
模块二: 45度角与一次函数、反比例函数结合
1、例题精讲
例题1.如图,在平面直角坐标系中,一次函数的图象分别交轴于点,直线与轴交于点,若,则直线的函数表达式是( )
【解答】解:方法1 构造等腰直角三角形,构造一线三垂直
易得A(1,0),B(0,-2),∴OA=1,OB=2.
如图①,过点A作AF⊥AB交BC于点F,过点F作FE⊥x轴于点E.
∵∠ABC=45°,∴△ABF是等腰直角三角形.∴AB=AF.
∵∠OAB+∠ABO=∠OAB+∠EAF=90°,
∴∠ABO=∠EAF.
∴△ABO≌△FAE(AAS).
∴AE=OB=2,EF=OA=1. ∴F(3,-1).
设直线BC的函数表达式为y=kx+b.将点B(0,-2),F(3,-1)的坐标分别代入,
得,解得
∴直线BC的函数表达式为.
方法2 构造等腰直角三角形,利用勾股定理列方程
易得A(1,0),B(0,-2),∴OA=1,OB=2,AB=.
如图②,过点A作AD⊥BC于点D.
∵∠ABC=45°,∴AD=AB=.
根据等面积法可得AC·OB=BC·AD,
设AC长为m,则2m=,
整理得,解得m=5或m=(舍去).
∴OC=6,则C(6,0).
∵直线BC过点B(0,-2),C(6,0),∴直线BC的函数表达式为.
例题2.如图,已知反比例函数(x>0)的图象经过点A(3,4),在该图象上找一点P,使∠POA=45°,则点P的坐标为 .
【解答】解:
方法1:作AE⊥y轴于E,将线段OA绕点O顺时针旋转90°得到OA′,作A′F⊥x轴于F,则△AOE≌△A′OF,可得OF=OE=4,A′F=AE=3,
即A′(4,-3),∵反比例函数y=(x>0)的图象经过点A(3,4),
所以由勾股定理可知:OA=5,
∴4=,OA=5,∴k=12,∴y=,
∴AA′的中点K(,),∴直线OK的解析式为y=x,
由,解得或,
∵点P在第一象限,∴P(2,),
故答案为(2,).
方法2 思路提示:如图②,构造一线三直角,易得C(7,1),再求点P的坐标.
方法3 思路提示:如图③,构造半角模型,设DE=x,利用1+(4-x)2=(x+3)2先求点E的坐标,再求点P的坐标.
2、跟进练习
练习1. 如图,在平面直角坐标系中,A(0,4)、B(6,0)为坐标轴上的点,点C为线段AB的中点,过点C作DC⊥x轴,垂足为D,点E为y轴负半轴上一点,连结CE交x轴于点F,且CF=FE.
(1)直接写出E点的坐标________;
(2)过点B作BG∥CE,交y轴于点G,交直线CD于点H,求四边形ECBG的面积;
(3)直线CD上是否存在点Q使得∠ABQ=45°,若存在,请求出点Q的坐标,若不存在,请说明理由.
【解答】:(1)∵CD⊥x轴,∴∠CDF=90°=∠EOF,又∵∠CFD=∠EFO,CF=EF,
∴△CDF≌△EOF(AAS),∴CD=OE,又∵A(0,4),B(6,0),∴OA=4,OB=6,
∵点C为AB的中点,CD∥y轴,∴CDOA=2,∴OE=2,∴E(0,﹣2);
(2)设直线CE的解析式为y=kx+b,∵C为AB的中点,A(0,4),B(6,0),
∴C(3,2),∴,解得,∴直线CE的解析式为yx﹣2,
∵BG∥CE,∴设直线BG的解析式为yx+m,∴6+m=0,∴m=﹣8,
∴G点的坐标为(0,﹣8),∴AG=12,
∴S四边形ECBG=S△ABG﹣S△ACE
AE×OD
6×3
=27.
(3)直线CD上存在点Q使得∠ABQ=45°,分两种情况:
如图1,当点Q在x轴的上方时,∠ABQ=45°,
过点A作AM⊥AB,交BQ于点M,过点M作MH⊥y轴于点H,
则△ABM为等腰直角三角形,
∴AM=AB,∵∠HAM+∠OAB=∠OAB+∠ABO=90°,
∴∠HAM=∠ABO,∵∠AHM=∠AOB=90°,∴△AMH≌△BAO(AAS),
∴MH=AO=4,AH=BO=6,∴OH=AH+OA=6+4=10,∴M(4,10),
∵B(6,0),∴直线BM的解析式为y=﹣5x+30,∵C(3,2),CD∥y轴,∴C点的横坐标为3,
∴y=﹣5×3+30=15,∴Q(3,15).
如图2,当点Q在x轴下方时,∠ABQ=45°,
过点A作AN⊥AB,交BQ于点N,过点N作NG⊥y轴于点G,
同理可得△ANG≌△BAO,∴NG=AO=4,AG=OB=6,
∴N(﹣4,﹣2),∴直线BN的解析式为yx,∴Q(3,).
综上所述,点Q的坐标为(3,15)或(3,).
练习2. 如图1,在平面直角坐标系中,已知直线AO与直线AC的表达式分别为:y=x、y=2x﹣6.
(1)直接写出点A的坐标为________.
(2)若点M在直线AC上,点N在直线OA上,且MN∥y轴,MN=OA,求点N的坐标.
(3)如图2,若点B在x轴正半轴上,当△BOC的面积等于△AOC面积的一半时,求∠ACO+∠BCO的大小.
【解答】(1)联立和得:
解得
A点的坐标为(4,2);
(2)∵A点的坐标为(4,2)
∴OA=,∴MN=OA=2,∵点M在直线AC上,点N在直线OA上,且MN//y轴,
∴设M的坐标为(a,2a-6),则N的坐标为(a,),
则存在以下两种情况:
①当M在N点下方时,如图3,
则MN=-(2a-6)=2,解得a=,∴N点的坐标为();
②当M在N点上方时,如图4,
则MN=(2a-6)-=2,解得a=,∴N点的坐标为();
综上所述,N的坐标为(),()
(3)∵△BOC与△AOC有相同的底边OC,
∴当△BOC的面积等于△AOC的面积一半时,△BOC的高OB的长度是△AOC的高的一半,∴OB=2,
设直线AC与x轴的交点为点D,则D(3,0),
作点B关于y轴的对称点G,则OG=0B=2,GD=5,∠BCO=∠GCO,
则∠ACO+∠BCO=∠ACO+∠GCO=∠ACG,连接GC,作DE⊥GC于点E,如图5
由勾股定理可得:GC=,DC=,
在△CGD中,由等面积法可得:OC DG=DE GC,可得DE=,
在Rt△DEC中,由勾股定理可得EC=,
∴ED=EC,∴∠ECD=45°,即∠ACO+∠BCO=45°.
练习3.综合与实践:
数学实践活动,是一种非常有效的学习方式,通过活动可以激发我们的学习兴趣,提高动手动脑能力,拓展思维空间,丰富数学体验,让我们一起动手来折一折、转一转、剪一剪,体会活动带给我们的乐趣.
折一折:将正方形纸片ABCD折叠,使边AB,AD都落在对角线AC上,展开得折痕AE,AF,连接EF,如图①.
(1)∠EAF=______°,写出图中两个等腰三角形:__________(不需要添加字母);
转一转:将图①中的∠EAF绕点A旋转,使它的两边分别交边BC,CD于点P,Q,连接PQ,如图②.
(2)判断线段BP,PQ,DQ之间的数量关系并证明;
(3)连接正方形对角线BD,若图②中的∠PAQ的边AP,AQ分别交对角线BD于点M,点N,如图③,求的值.
【解答】(1)∵四边形ABCD是正方形,∴AB=AD=BC=CD,∠BAD=90°,
∴ABC,△ADC都是等腰三角形,∵∠BAE=∠CAE,∠DAF=∠CAF,
∴∠EAF=(∠BAC+∠DAC)=45°,
∵∠BAE=∠DAF=22.5°,∠B=∠D=90°,AB=AD,∴△BAE≌△DAF(ASA),
∴BE=DF,AE=AF,∵CB=CD,∴CE=CF,∴△AEF,△CEF都是等腰三角形,
故答案为:45;△AEF,△EFC,△ABC,△ADC
(2)PQ=BP+DQ.
证明:如图②中,延长CB到T,使得BT=DQ.
∵AD=AB,∠ADQ=∠ABT=90°,DQ=BT,
∴△ADQ≌△ABT(SAS),∴AT=AQ,∠DAQ=∠BAT,
∵∠PAQ=45°,∴∠PAT=∠BAP+∠BAT=∠BAP+∠DAQ=45°,∴∠PAT=∠PAQ=45°,∵AP=AP,∴△PAT≌△PAQ(SAS),∴PQ=PT,
∵PT=PB+BT=PB+DQ,∴PQ=BP+DQ
(3)∵四边形ABCD是正方形,
∴∠ABM=∠ACQ=∠BAC=45°,AC=AB,∵∠BAC=∠PAQ=45°,∴∠BAM=∠CAQ,
∴△CAQ∽△BAM,∴.
模块三: 45度角与二次函数、圆结合
1、例题精讲
例题1.如图,抛物线与x轴交于、B两点,与y轴交于点C,对称轴为.
(1)求抛物线的解析式;
(2)点D在抛物线的对称轴上,若, 求点D的坐标;
(3)点M在抛物线上,若中有一个内角为,请直接写出点M 的坐标.
【解答】
(1)解:抛物线与x轴交于、B两点,对称轴为.
∴,将,代入得:,解得:,
∴抛物线的解析式为;
(2)当时,,即,设直线的解析式为,代入,得:,解得:,∴直线的解析式为,令中边上的高为,中边上的高为,∵,即,则,∴,∴直线的解析式为,将代入,可得,解得,
∴直线的解析式为,∵点在抛物线的对称轴上,∴当时,,
∴点的坐标为;
(3)以为斜边,在上方作等腰,则,设,
过点作轴,,则,而,
∴,∴,∴,,
∵,即:,∴,则,即,
①当时,点为直线与抛物线的交点,
同(2)可得直线的解析式为:,
联立得直线与抛物线得,解得:或(舍去),
即:点的坐标为;
②当时,点为直线与抛物线的交点,
同上,可得点的坐标为;
③当时,
∵,∴点以点为圆心,为半径的圆上,
即点为与抛物线的交点,
设,∴,
即:,整理得:,
,,,
,,解得:(舍去)或或或(舍去),当时,点的坐标为,当时,点的坐标为,
即:点的坐标为或;
综上:点的坐标为或或或
例题2.如图,已知在平面直角坐标系xOy中,抛物线与x轴交于点A、B(点A在点B右侧),与y轴交于点C(0,-3),且OA=2OC.
(1)求这条抛物线的表达式及顶点M的坐标;
(2)求的值;
(3)如果点D在这条抛物线的对称轴上,且∠CAD=45 ,求点D的坐标.
【解答】
(1)∵C(0,-3),∴OC=3.y=x2+bx-3.∵OA=2OC,∴OA=6.
∵a=>0,点A在点B右侧,抛物线与y轴交点C(0,-3).∴A(6,0).∴0=×36+6b-3,∴b=-1.
∴y=x2-x-3,∴y=(x-2)2-4,∴M(2,-4).
(2)如图1,过点M作MH⊥x轴,垂足为点H,交AC于点N,过点N作NE⊥AM于点E,垂足为点E.
∴∠AHM=∠NEM=90°.在Rt△AHM中,HM=AH=4,由勾股定理,得
AM=4,∴∠AMH=∠HAM=45°.
设直线AC的解析式为y=kx+b,由题意,得
,解得:,∴直线AC的表达式为y=x-3.
当x=2时,y=-2,∴N(2,-2).∴MN=2.∵∠NEM=90°,∠NME=45°,∴∠MNE=∠NME=45°,
∴NE=ME.在Rt△MNE中,∴NE2+ME2=NM2,∴ME=NE=.∴AE=AM-ME=3
在Rt△AEN中,tan∠MAC=.
(3)如图2,
①当D点在AC上方时,
∵∠CAD1=∠D1AH+∠HAC=45°,且∠HAM=∠HAC+∠CAM=45°,
∴∠D1AH=∠CAM,∴tan∠D1AH=tan∠MAC=.
∵点D1在抛物线的对称轴直线x=2上,∴D1H⊥AH,
∴AH=4.在Rt△AHD1中,
D1H=AH tan∠D1AH=4×=.∴D1(2,);
②当D点在AC下方时,
∵∠D2AC=∠D2AM+∠MAC=45°,且∠AMH=∠D2AM+∠AD2M=45°,
∴∠MAC=∠AD2M.∴tan∠AD2H=tan∠MAC=.在Rt△D2AH中,D2H=.
∴D2(2,-12).
综上所述:D1(2,);D2(2,-12).
2、跟进练习
练习1.如图,在平面直角坐标系xOy中,抛物线y=ax2+bx﹣3(a≠0)与x轴交于点A(﹣1,0)和点B,且OB=3OA,与y轴交于点C,此抛物线顶点为点D.
(1)求抛物线的表达式及点D的坐标;
(2)如果点E是y轴上的一点(点E与点C不重合),当BE⊥DE时,求点E的坐标;
(3)如果点F是抛物线上的一点.且∠FBD=135°,求点F的坐标.
【解答】解:
⑴ ,∴D(1,-4);
⑵ 设E(0,t),则,∴E(0,-1);
⑶ 又⑵得∠BCD=90°,∴△BCD≌△BEG,EG=CD=,BE=BC=,∠DBG=135°,
∴G(,),又B(3,0),∴BF:,∴.
故答案为(1)D(1,-4);(2)E(0,1);(3)(-4,21)
练习2. 在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,2),它的顶点为D(1,m),且tan∠COD=.
(1)求m的值及抛物线的表达式;
(2)将此抛物线向上平移后与x轴正半轴交于点A,与y轴交于点B,且OA=OB.若点A是由原抛物线上的点E平移所得,求点E的坐标;
(3)在(2)的条件下,点P是抛物线对称轴上的一点(位于x轴上方),且∠APB=45°.求P点的坐标.
【解答】解:(1)作DH⊥y轴,垂足为H,∵D(1,m)(),∴DH= m,HO=1.∵,∴,∴m=3. ∴抛物线的顶点为D(1,3).
又∵抛物线与y轴交于点C(0,2),∴(2∴∴抛物线的表达式为.
(2)∵将此抛物线向上平移,∴设平移后的抛物线表达式为.
则它与y轴交点B(0,2+k).∵平移后的抛物线与x轴正半轴交于点A,且OA=OB,
∴A点的坐标为(2+k,0). ∴.∴.
∵,∴.∴A(3,0),抛物线向上平移了1个单位.
∵点A由点E向上平移了1个单位所得,∴E(3,-1).
(3)由(2)得A(3,0),B(0, 3),∴.
∵点P是抛物线对称轴上的一点(位于x轴上方),且∠APB=45°,原顶点D(1,3),
∴设P(1,y),设对称轴与AB的交点为M,与x轴的交点为H,则H(1,0).
∵A(3,0),B(0, 3),∴∠OAB=45°, ∴∠AMH=45°.
∴M(1,2). ∴.∵∠BMP=∠AMH, ∴∠BMP=45°.
∵∠APB=45°, ∴∠BMP=∠APB.∵∠B=∠B,∴△BMP∽△BPA.
∴.∴
∴.∴(舍).
∴
练习3.已知:如图,在中,是直径,点C在圆上,且满足弧弧.
(1)如图1,求证:;
(2)如图2,点D、E,⊙O上,连接、、、、,.求证:;
(3)在(2)的条件下,点F在上,且满足,M、G分别是、与的交点,连接交于点H,若tan∠,,求的长.
【解答】解:(1)证明:如图1中,
∵AB是直径,∴∠ACB=90°,∵,∴BC=AC,∴∠A=∠B=45°;
(2)证明:
∵CE=BD,∴,∵,∴,∴CD=AE;
(3)解:如图3中,设BC=AC=12m.延长BF交⊙O于点K,连接AK.
∵EC=BD,AC=BC,AE=CD,∴△AEC≌△CDB(SSS),
∴∠ACE=∠CBD,∵∠DBF=∠BAE=∠ECB,
∴∠DBF+∠CBF=∠ECB+∠BCA,∴∠CBF=∠ACB=90°,
∵∠K=∠CBK=∠ACB=90°,∴四边形AKBC是矩形,
∵CA=CB,∴四边形AKBC是正方形,∴BK=BC=12m,
将△ACM绕点A逆时针旋转90°得到△AKN,∵,∴,
∴∠EAD=∠CAB=45°,∵∠KAF+∠CAM=∠KAF+∠KAM=45°,
∴∠FAM=∠FAN=45°,∵AF=AF,AM=AN,∴△FAM≌△FAN(SAS),
∴MF=FN=FK+KN=FK+CM,∵tan∠BFM==,∴可以假设BM=3k,BF=4k,则FM=5k,
∵CM=12m 3k,FK=12m 4k,∴24m 7k=5k,∴k=2m,∴BM=CM=6m,
∵,∴∠BCD=∠CAE,∵∠BCD+∠ACG=90°,∴∠CAE+∠ACG=90°,∴∠CGA=90°,
∴CH⊥AM,∵AC=CB,∠ACM=∠CBH=90°,∠BCH=∠CAM,∴△CBH≌△ACM(ASA),
∴CH=AM,∴tan∠CAM===,∵AG=4,∴CG=2,∵tan∠MCG==,
∴MG=1,
∴AM=CH=5,
∴GH=CH CG=5 2=3.
一、前置学习
1、一线三等角
如图1,,,过点B作于点C,过点D作于点E.由,得.又,可以推理得到.进而得到DE,.我们把这个数学模型称为“K字”模型或“一线三等角”模型
2、正方形内半角模型
如图2,在正方形ABCD中,点E、F分别在边BC、CD上,∠EAF=45°,连接AE、AF、EF。则可将△ADF绕点A点顺时针旋转90°至△ABG处,使得AD和AB重合,即△ADF ≌△ABG,则有以下结论成立:
①△AEG ≌△AEF;
②BE+DF=EF;
③∠AEF=∠AEB,∠AFE=∠AFD;
图2 图3
3、方法归纳
(1)遇到45°→构造直角三角形→构造“一线三直角”
遇到45°→构造半角模型
遇到45°→构造圆心角为90度的圆
学习过程
模块一: 45度角问题初探
1、例题精讲
例题1.四边形 ABCD 中,AB∥CD,AB=4,BC=3,∠ABC=90°,∠ADB=45°.
求 CD 的长.
【解答】解:
方法1:构造一线三等角,利用相似求CD的长
如图,作,延长CD到点F,连接AF,使得∠CFA=45°,延长DC到点G,连接BG,使得∠BGD=45°,可证△ADF∽△DBG,,,在Rt△BCG中,,
△ADF∽△DBG
,即
,(舍),
方法2:构造直角三角形,构造母子型相似
如图,延长BA到点E,作
以E点为直角,作等腰直角三角形DEF,则△BAD∽△BDF,
, 设AE=x,BF=7+x,
在Rt△BED中,
,(舍),
=BE=4+x=
方法3:构造一线三垂直,利用A型相似求解
如图,延长BA到点F,作
过A点作交BD于点E,过E点作
则,
易证△EGB∽△DFB, ,设EG=x,
,,(舍),
=4+x=
方法4:构造一线三垂直,利用X型相似求解
如图,过A点作交BD于点E,过E点作,
,则,,
,CG=BF=4-x
易证△DGE∽△BFE, , ,
,(舍),,
=DG+CG=7-2x=
方法5:构造一线三垂直,利用相似求解
如图,过B点作交DA延长线于点E,可证
,,,
,
易证△DGA∽△DHE,
,(舍),,
=
例题2.如图,在矩形ABCD中,AB=2,BC=4,点E,F分别在BC,CD上,若
AE=,∠EAF=45°,则AF的长为 .
【解答】解:
方法1:构造等腰直角三角形,列二元一次方程组求解
如图①,过点E作EH⊥AF于点H,过点H作MN⊥BC,分别交AD,BC于点M,N.易证△AMH≌△HNE.
设MH=NE=x,AM=HN=y,
那么,解得 ,
方法2:构造等腰直角三角形,利用全等、相似求解
如图②,过点E作EG⊥AE,交AF于点G,作GH⊥BC于点H,易证△ABE≌△EHG.
∴EH=AB=2,GH=BE=1,
∴HC=1 ,
,
,
方法3:利用半角模型求解(先构造半角模型,借助△ADF的中位线求出DF,再求AF)
用到一个结论:
如图③,已知正方形ABMN,E,G分别是BM,MN上的点,
且∠EAG=45°,那么BE+NG=EG.
按照这个结论,先构造半角模型,如图④,取BC,AD的中点M,N,
连接MN,交AF于点G,连结EG.
设NG=m,那么EG=BE+NG=1+m.
在Rt△GEM中,GM=2-m,EM=1,EG=1+m.
由勾股定理,得,解得.
易得NG是△ADF的中位线,
∴DF=,∴
方法4:构造两个等腰三角形求解
如图⑤,易知BE=1,取AB的中点M,连结ME.
在AD上截取ND=DF,连结NF.
∵四边形ABCD是矩形,
∴∠D=∠BAD=∠B=90°,AD=BC=4.
设DF=DN=x,则NF=,AN=4-x.
∵AB=2,
∴AM=BM=BE=1.
∴.
∵∠EAF=45°,∴∠1+∠3=45°.
又∠2+∠3=45°,∴∠1=∠2.
又∵∠AME=∠FNA=135°,
∴△AME∽△FNA
∴. ,∴解得x=4/3. ∴.
2、跟进练习
练习1. 如图,在矩形中,,是边上一点,且,连接.若,则的长为( )
B. C. D.
【解答】解:
作交的延长线于点,则,
∵,∴,
∴,∵四边形是矩形,∴,
∵,,∴,
∴,
∵,,∴,
∴,∴,
∴,∴,故选:.
练习2. 已知是直角三角形,连接以为底作直角三角形且是边上的一点,连接和且则长为 .
【解答】解:
将线段绕点顺时针旋转,得到线段,连接,HE,
是等腰直角三角形,∴∠HBD=45°
∵∠FBD=45°∴点B、F、H共线又是等腰直角三角形,
,,,,,,
,
,,,,,故答案为:.
练习3. 如图,△ABC为等腰直角三角形,,是上一点,交直线于点,且,,点为的中点,连接,则的长为( )
A. B. C. D.
【解答】解:如图,过点作交延长线于,
∵,∴, ∵,∴,
∴是等腰直角三角形, ∴,
设,则,由勾股定理得,,,
,∴,
整理得,
解得,(不合,舍去),
∴,∴,∵点为的中点,∴,故选:.
模块二: 45度角与一次函数、反比例函数结合
1、例题精讲
例题1.如图,在平面直角坐标系中,一次函数的图象分别交轴于点,直线与轴交于点,若,则直线的函数表达式是( )
【解答】解:方法1 构造等腰直角三角形,构造一线三垂直
易得A(1,0),B(0,-2),∴OA=1,OB=2.
如图①,过点A作AF⊥AB交BC于点F,过点F作FE⊥x轴于点E.
∵∠ABC=45°,∴△ABF是等腰直角三角形.∴AB=AF.
∵∠OAB+∠ABO=∠OAB+∠EAF=90°,
∴∠ABO=∠EAF.
∴△ABO≌△FAE(AAS).
∴AE=OB=2,EF=OA=1. ∴F(3,-1).
设直线BC的函数表达式为y=kx+b.将点B(0,-2),F(3,-1)的坐标分别代入,
得,解得
∴直线BC的函数表达式为.
方法2 构造等腰直角三角形,利用勾股定理列方程
易得A(1,0),B(0,-2),∴OA=1,OB=2,AB=.
如图②,过点A作AD⊥BC于点D.
∵∠ABC=45°,∴AD=AB=.
根据等面积法可得AC·OB=BC·AD,
设AC长为m,则2m=,
整理得,解得m=5或m=(舍去).
∴OC=6,则C(6,0).
∵直线BC过点B(0,-2),C(6,0),∴直线BC的函数表达式为.
例题2.如图,已知反比例函数(x>0)的图象经过点A(3,4),在该图象上找一点P,使∠POA=45°,则点P的坐标为 .
【解答】解:
方法1:作AE⊥y轴于E,将线段OA绕点O顺时针旋转90°得到OA′,作A′F⊥x轴于F,则△AOE≌△A′OF,可得OF=OE=4,A′F=AE=3,
即A′(4,-3),∵反比例函数y=(x>0)的图象经过点A(3,4),
所以由勾股定理可知:OA=5,
∴4=,OA=5,∴k=12,∴y=,
∴AA′的中点K(,),∴直线OK的解析式为y=x,
由,解得或,
∵点P在第一象限,∴P(2,),
故答案为(2,).
方法2 思路提示:如图②,构造一线三直角,易得C(7,1),再求点P的坐标.
方法3 思路提示:如图③,构造半角模型,设DE=x,利用1+(4-x)2=(x+3)2先求点E的坐标,再求点P的坐标.
2、跟进练习
练习1. 如图,在平面直角坐标系中,A(0,4)、B(6,0)为坐标轴上的点,点C为线段AB的中点,过点C作DC⊥x轴,垂足为D,点E为y轴负半轴上一点,连结CE交x轴于点F,且CF=FE.
(1)直接写出E点的坐标________;
(2)过点B作BG∥CE,交y轴于点G,交直线CD于点H,求四边形ECBG的面积;
(3)直线CD上是否存在点Q使得∠ABQ=45°,若存在,请求出点Q的坐标,若不存在,请说明理由.
【解答】:(1)∵CD⊥x轴,∴∠CDF=90°=∠EOF,又∵∠CFD=∠EFO,CF=EF,
∴△CDF≌△EOF(AAS),∴CD=OE,又∵A(0,4),B(6,0),∴OA=4,OB=6,
∵点C为AB的中点,CD∥y轴,∴CDOA=2,∴OE=2,∴E(0,﹣2);
(2)设直线CE的解析式为y=kx+b,∵C为AB的中点,A(0,4),B(6,0),
∴C(3,2),∴,解得,∴直线CE的解析式为yx﹣2,
∵BG∥CE,∴设直线BG的解析式为yx+m,∴6+m=0,∴m=﹣8,
∴G点的坐标为(0,﹣8),∴AG=12,
∴S四边形ECBG=S△ABG﹣S△ACE
AE×OD
6×3
=27.
(3)直线CD上存在点Q使得∠ABQ=45°,分两种情况:
如图1,当点Q在x轴的上方时,∠ABQ=45°,
过点A作AM⊥AB,交BQ于点M,过点M作MH⊥y轴于点H,
则△ABM为等腰直角三角形,
∴AM=AB,∵∠HAM+∠OAB=∠OAB+∠ABO=90°,
∴∠HAM=∠ABO,∵∠AHM=∠AOB=90°,∴△AMH≌△BAO(AAS),
∴MH=AO=4,AH=BO=6,∴OH=AH+OA=6+4=10,∴M(4,10),
∵B(6,0),∴直线BM的解析式为y=﹣5x+30,∵C(3,2),CD∥y轴,∴C点的横坐标为3,
∴y=﹣5×3+30=15,∴Q(3,15).
如图2,当点Q在x轴下方时,∠ABQ=45°,
过点A作AN⊥AB,交BQ于点N,过点N作NG⊥y轴于点G,
同理可得△ANG≌△BAO,∴NG=AO=4,AG=OB=6,
∴N(﹣4,﹣2),∴直线BN的解析式为yx,∴Q(3,).
综上所述,点Q的坐标为(3,15)或(3,).
练习2. 如图1,在平面直角坐标系中,已知直线AO与直线AC的表达式分别为:y=x、y=2x﹣6.
(1)直接写出点A的坐标为________.
(2)若点M在直线AC上,点N在直线OA上,且MN∥y轴,MN=OA,求点N的坐标.
(3)如图2,若点B在x轴正半轴上,当△BOC的面积等于△AOC面积的一半时,求∠ACO+∠BCO的大小.
【解答】(1)联立和得:
解得
A点的坐标为(4,2);
(2)∵A点的坐标为(4,2)
∴OA=,∴MN=OA=2,∵点M在直线AC上,点N在直线OA上,且MN//y轴,
∴设M的坐标为(a,2a-6),则N的坐标为(a,),
则存在以下两种情况:
①当M在N点下方时,如图3,
则MN=-(2a-6)=2,解得a=,∴N点的坐标为();
②当M在N点上方时,如图4,
则MN=(2a-6)-=2,解得a=,∴N点的坐标为();
综上所述,N的坐标为(),()
(3)∵△BOC与△AOC有相同的底边OC,
∴当△BOC的面积等于△AOC的面积一半时,△BOC的高OB的长度是△AOC的高的一半,∴OB=2,
设直线AC与x轴的交点为点D,则D(3,0),
作点B关于y轴的对称点G,则OG=0B=2,GD=5,∠BCO=∠GCO,
则∠ACO+∠BCO=∠ACO+∠GCO=∠ACG,连接GC,作DE⊥GC于点E,如图5
由勾股定理可得:GC=,DC=,
在△CGD中,由等面积法可得:OC DG=DE GC,可得DE=,
在Rt△DEC中,由勾股定理可得EC=,
∴ED=EC,∴∠ECD=45°,即∠ACO+∠BCO=45°.
练习3.综合与实践:
数学实践活动,是一种非常有效的学习方式,通过活动可以激发我们的学习兴趣,提高动手动脑能力,拓展思维空间,丰富数学体验,让我们一起动手来折一折、转一转、剪一剪,体会活动带给我们的乐趣.
折一折:将正方形纸片ABCD折叠,使边AB,AD都落在对角线AC上,展开得折痕AE,AF,连接EF,如图①.
(1)∠EAF=______°,写出图中两个等腰三角形:__________(不需要添加字母);
转一转:将图①中的∠EAF绕点A旋转,使它的两边分别交边BC,CD于点P,Q,连接PQ,如图②.
(2)判断线段BP,PQ,DQ之间的数量关系并证明;
(3)连接正方形对角线BD,若图②中的∠PAQ的边AP,AQ分别交对角线BD于点M,点N,如图③,求的值.
【解答】(1)∵四边形ABCD是正方形,∴AB=AD=BC=CD,∠BAD=90°,
∴ABC,△ADC都是等腰三角形,∵∠BAE=∠CAE,∠DAF=∠CAF,
∴∠EAF=(∠BAC+∠DAC)=45°,
∵∠BAE=∠DAF=22.5°,∠B=∠D=90°,AB=AD,∴△BAE≌△DAF(ASA),
∴BE=DF,AE=AF,∵CB=CD,∴CE=CF,∴△AEF,△CEF都是等腰三角形,
故答案为:45;△AEF,△EFC,△ABC,△ADC
(2)PQ=BP+DQ.
证明:如图②中,延长CB到T,使得BT=DQ.
∵AD=AB,∠ADQ=∠ABT=90°,DQ=BT,
∴△ADQ≌△ABT(SAS),∴AT=AQ,∠DAQ=∠BAT,
∵∠PAQ=45°,∴∠PAT=∠BAP+∠BAT=∠BAP+∠DAQ=45°,∴∠PAT=∠PAQ=45°,∵AP=AP,∴△PAT≌△PAQ(SAS),∴PQ=PT,
∵PT=PB+BT=PB+DQ,∴PQ=BP+DQ
(3)∵四边形ABCD是正方形,
∴∠ABM=∠ACQ=∠BAC=45°,AC=AB,∵∠BAC=∠PAQ=45°,∴∠BAM=∠CAQ,
∴△CAQ∽△BAM,∴.
模块三: 45度角与二次函数、圆结合
1、例题精讲
例题1.如图,抛物线与x轴交于、B两点,与y轴交于点C,对称轴为.
(1)求抛物线的解析式;
(2)点D在抛物线的对称轴上,若, 求点D的坐标;
(3)点M在抛物线上,若中有一个内角为,请直接写出点M 的坐标.
【解答】
(1)解:抛物线与x轴交于、B两点,对称轴为.
∴,将,代入得:,解得:,
∴抛物线的解析式为;
(2)当时,,即,设直线的解析式为,代入,得:,解得:,∴直线的解析式为,令中边上的高为,中边上的高为,∵,即,则,∴,∴直线的解析式为,将代入,可得,解得,
∴直线的解析式为,∵点在抛物线的对称轴上,∴当时,,
∴点的坐标为;
(3)以为斜边,在上方作等腰,则,设,
过点作轴,,则,而,
∴,∴,∴,,
∵,即:,∴,则,即,
①当时,点为直线与抛物线的交点,
同(2)可得直线的解析式为:,
联立得直线与抛物线得,解得:或(舍去),
即:点的坐标为;
②当时,点为直线与抛物线的交点,
同上,可得点的坐标为;
③当时,
∵,∴点以点为圆心,为半径的圆上,
即点为与抛物线的交点,
设,∴,
即:,整理得:,
,,,
,,解得:(舍去)或或或(舍去),当时,点的坐标为,当时,点的坐标为,
即:点的坐标为或;
综上:点的坐标为或或或
例题2.如图,已知在平面直角坐标系xOy中,抛物线与x轴交于点A、B(点A在点B右侧),与y轴交于点C(0,-3),且OA=2OC.
(1)求这条抛物线的表达式及顶点M的坐标;
(2)求的值;
(3)如果点D在这条抛物线的对称轴上,且∠CAD=45 ,求点D的坐标.
【解答】
(1)∵C(0,-3),∴OC=3.y=x2+bx-3.∵OA=2OC,∴OA=6.
∵a=>0,点A在点B右侧,抛物线与y轴交点C(0,-3).∴A(6,0).∴0=×36+6b-3,∴b=-1.
∴y=x2-x-3,∴y=(x-2)2-4,∴M(2,-4).
(2)如图1,过点M作MH⊥x轴,垂足为点H,交AC于点N,过点N作NE⊥AM于点E,垂足为点E.
∴∠AHM=∠NEM=90°.在Rt△AHM中,HM=AH=4,由勾股定理,得
AM=4,∴∠AMH=∠HAM=45°.
设直线AC的解析式为y=kx+b,由题意,得
,解得:,∴直线AC的表达式为y=x-3.
当x=2时,y=-2,∴N(2,-2).∴MN=2.∵∠NEM=90°,∠NME=45°,∴∠MNE=∠NME=45°,
∴NE=ME.在Rt△MNE中,∴NE2+ME2=NM2,∴ME=NE=.∴AE=AM-ME=3
在Rt△AEN中,tan∠MAC=.
(3)如图2,
①当D点在AC上方时,
∵∠CAD1=∠D1AH+∠HAC=45°,且∠HAM=∠HAC+∠CAM=45°,
∴∠D1AH=∠CAM,∴tan∠D1AH=tan∠MAC=.
∵点D1在抛物线的对称轴直线x=2上,∴D1H⊥AH,
∴AH=4.在Rt△AHD1中,
D1H=AH tan∠D1AH=4×=.∴D1(2,);
②当D点在AC下方时,
∵∠D2AC=∠D2AM+∠MAC=45°,且∠AMH=∠D2AM+∠AD2M=45°,
∴∠MAC=∠AD2M.∴tan∠AD2H=tan∠MAC=.在Rt△D2AH中,D2H=.
∴D2(2,-12).
综上所述:D1(2,);D2(2,-12).
2、跟进练习
练习1.如图,在平面直角坐标系xOy中,抛物线y=ax2+bx﹣3(a≠0)与x轴交于点A(﹣1,0)和点B,且OB=3OA,与y轴交于点C,此抛物线顶点为点D.
(1)求抛物线的表达式及点D的坐标;
(2)如果点E是y轴上的一点(点E与点C不重合),当BE⊥DE时,求点E的坐标;
(3)如果点F是抛物线上的一点.且∠FBD=135°,求点F的坐标.
【解答】解:
⑴ ,∴D(1,-4);
⑵ 设E(0,t),则,∴E(0,-1);
⑶ 又⑵得∠BCD=90°,∴△BCD≌△BEG,EG=CD=,BE=BC=,∠DBG=135°,
∴G(,),又B(3,0),∴BF:,∴.
故答案为(1)D(1,-4);(2)E(0,1);(3)(-4,21)
练习2. 在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,2),它的顶点为D(1,m),且tan∠COD=.
(1)求m的值及抛物线的表达式;
(2)将此抛物线向上平移后与x轴正半轴交于点A,与y轴交于点B,且OA=OB.若点A是由原抛物线上的点E平移所得,求点E的坐标;
(3)在(2)的条件下,点P是抛物线对称轴上的一点(位于x轴上方),且∠APB=45°.求P点的坐标.
【解答】解:(1)作DH⊥y轴,垂足为H,∵D(1,m)(),∴DH= m,HO=1.∵,∴,∴m=3. ∴抛物线的顶点为D(1,3).
又∵抛物线与y轴交于点C(0,2),∴(2∴∴抛物线的表达式为.
(2)∵将此抛物线向上平移,∴设平移后的抛物线表达式为.
则它与y轴交点B(0,2+k).∵平移后的抛物线与x轴正半轴交于点A,且OA=OB,
∴A点的坐标为(2+k,0). ∴.∴.
∵,∴.∴A(3,0),抛物线向上平移了1个单位.
∵点A由点E向上平移了1个单位所得,∴E(3,-1).
(3)由(2)得A(3,0),B(0, 3),∴.
∵点P是抛物线对称轴上的一点(位于x轴上方),且∠APB=45°,原顶点D(1,3),
∴设P(1,y),设对称轴与AB的交点为M,与x轴的交点为H,则H(1,0).
∵A(3,0),B(0, 3),∴∠OAB=45°, ∴∠AMH=45°.
∴M(1,2). ∴.∵∠BMP=∠AMH, ∴∠BMP=45°.
∵∠APB=45°, ∴∠BMP=∠APB.∵∠B=∠B,∴△BMP∽△BPA.
∴.∴
∴.∴(舍).
∴
练习3.已知:如图,在中,是直径,点C在圆上,且满足弧弧.
(1)如图1,求证:;
(2)如图2,点D、E,⊙O上,连接、、、、,.求证:;
(3)在(2)的条件下,点F在上,且满足,M、G分别是、与的交点,连接交于点H,若tan∠,,求的长.
【解答】解:(1)证明:如图1中,
∵AB是直径,∴∠ACB=90°,∵,∴BC=AC,∴∠A=∠B=45°;
(2)证明:
∵CE=BD,∴,∵,∴,∴CD=AE;
(3)解:如图3中,设BC=AC=12m.延长BF交⊙O于点K,连接AK.
∵EC=BD,AC=BC,AE=CD,∴△AEC≌△CDB(SSS),
∴∠ACE=∠CBD,∵∠DBF=∠BAE=∠ECB,
∴∠DBF+∠CBF=∠ECB+∠BCA,∴∠CBF=∠ACB=90°,
∵∠K=∠CBK=∠ACB=90°,∴四边形AKBC是矩形,
∵CA=CB,∴四边形AKBC是正方形,∴BK=BC=12m,
将△ACM绕点A逆时针旋转90°得到△AKN,∵,∴,
∴∠EAD=∠CAB=45°,∵∠KAF+∠CAM=∠KAF+∠KAM=45°,
∴∠FAM=∠FAN=45°,∵AF=AF,AM=AN,∴△FAM≌△FAN(SAS),
∴MF=FN=FK+KN=FK+CM,∵tan∠BFM==,∴可以假设BM=3k,BF=4k,则FM=5k,
∵CM=12m 3k,FK=12m 4k,∴24m 7k=5k,∴k=2m,∴BM=CM=6m,
∵,∴∠BCD=∠CAE,∵∠BCD+∠ACG=90°,∴∠CAE+∠ACG=90°,∴∠CGA=90°,
∴CH⊥AM,∵AC=CB,∠ACM=∠CBH=90°,∠BCH=∠CAM,∴△CBH≌△ACM(ASA),
∴CH=AM,∴tan∠CAM===,∵AG=4,∴CG=2,∵tan∠MCG==,
∴MG=1,
∴AM=CH=5,
∴GH=CH CG=5 2=3.
同课章节目录
