华师大八年级上册第14章14.1勾股定理1直角三角形三边的关系
文档属性
| 名称 | 华师大八年级上册第14章14.1勾股定理1直角三角形三边的关系 |  | |
| 格式 | doc | ||
| 文件大小 | 230.0KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-21 17:06:59 | ||
图片预览


文档简介
登陆21世纪教育 助您教考全无忧
华师大版八年级上册第14章第1节14.1.1直角三角形三边的关系课时练习
一、单选题(共15小题)
1.下列说法正确的是( )
A.若 a、b、c是△ABC的三边,则a2+b2=c2
B.若 a、b、c是Rt△ABC的三边,则a2+b2=c2
C.若 a、b、c是Rt△ABC的三边, ,则a2+b2=c2
D.若 a、b、c是Rt△ABC的三边, ,则a2+b2=c2
答案:D
解答:两直角边的平方和等于斜边的平方,所以D正确.
分析:利用勾股定理正确书写三角形三边关系的关键是看清谁是直角.
2.Rt△ABC的三条边长分别是、、,则下列各式成立的是( )
A. B. C. D.
答案:B
解答:由三角形三边关系得B正确,A、C错误,因为没有确定哪个角是直角,所以D不一定正确.
分析:本题考察三角形的三边关系和勾股定理.
3.如果直角三角形的两直角边长分别为k2-1,2k(k >1),那么它的斜边长是( )
A.2k B.k+1 C.k2-1 D.k2+1
答案:D
解答:由勾股定理,斜边长为
分析:能运用勾股定理解决有字母的代数式问题.
4.已知a,b,c为△ABC三边,且满足(a2-b2)(a2+b2-c2)=0,则它的形状为( )
A.直角三角形 B.等腰三角形
C.等腰直角三角形 D.等腰三角形或直角三角形
答案:D
解答:由关系式得或,因为,所以或,所以三角形的形状为等腰三角形或直角三角形.
分析:综合分析解析式得到的结论,并判断三角形的形状.
5.直角三角形中一直角边的长为9,另两边为连续自然数,则直角三角形的周长为( )
A.121 B.120 C.90 D.不能确定
答案:C
解答:设直角三角形的另一条直角边为,则斜边为,由勾股定理得,解之得,则其周长为,故选C.
分析:能够运用代数式求解勾股定理产生的方程,并得出正确结论.
6.△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长为( )
A.42 B.32 C.42 或 32 D.37 或 33
答案:C
解答:当高AD是在三角形的内部时,BD=,CD=,所以,所以△ABC的周长为15+13+14=42;当高AD是在三角形的外部时,BC=,所以△ABC的周长为15+13+4=32,故选C.
分析:能够分情况讨论问题是培养学生思辨能力的基本方法.
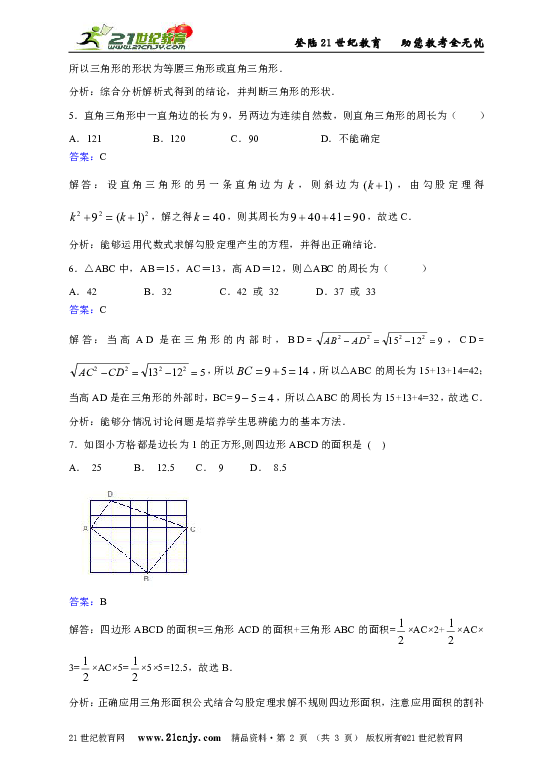
7.如图小方格都是边长为1的正方形,则四边形ABCD的面积是 ( )
A. 25 B. 12.5 C. 9 D. 8.5
答案:B
解答:四边形ABCD的面积=三角形ACD的面积+三角形ABC的面积=×AC×2+×AC×3=×AC×5=×5×5=12.5,故选B.
分析:正确应用三角形面积公式结合勾股定理求解不规则四边形面积,注意应用面积的割补法.
8.在平面直角坐标系中,已知点P的坐标是(3,4),则OP的长为( ) A.3 B.4 C.5 D.
答案:C
解答:
分析:利用平面直角坐标系,点的坐标的垂直特征,求解直角三角形的斜边.
9.若△ABC中,AB=25cm,AC=26cm,高AD=24,则BC的长为( )
A.17 B.3 C.17或3 D.以上都不对
答案:C
解答:当高AD是在三角形的内部时,BD=,CD=,所以,;当高AD是在三角形的外部时,BC=,故选C.
分析:三角形的高把三角形分为两个直角三角形,这个高可能在三角形的内部或在外部,分情况讨论求解,是培养学生矛盾的两面性的逻辑思维的方法.
10.已知a、b、c是三角形的三边长,如果满足则三角形的
形状是( )
A.底与边不相等的等腰三角形 B.等边三角形
C.钝角三角形 D.直角三角形
答案:D
解答:由题意,,,,所以,,,所以,所以三角形是直角三角形.
分析:由非负和为零,确定、、的值,并用勾股定理的逆定理判断三角形的形状.
11.下列各组数中,能构成直角三角形的是( )
A.4,5,6 B.1,1, C.6,8,11 D.5,12,23
答案:B
解答:符合的三角形是直角三角形,题目当中只有B符合此关系式,故选B.
分析:利用判断直角三角形的方法,即勾股定理的逆定理进行判断.
12.在Rt△ABC中,∠C=90°,a=12,b=16,则c的长为( )
A.26 B.18 C.20 D.21
答案:C
解答:由勾股定理,,故选C.
分析:运用勾股定理进行计算.
13.等边三角形的边长为2,则该三角形的面积为( )
A. B. C. D.3
答案:B
解答:等边三角形的高为,面积为,故选B.
分析:利用等边三角形三线合一,构造直角三角形,并用勾股定理求出高长,最后求出面积.
14.在Rt△ABC中,∠C=90°,∠B=45°,c=10,则a的长为( )
A.5 B. C. D.
答案:C
解答:由题意,则,所以,所以,故选C.
分析:关于特殊的直角三角形,如等腰直角三角形有特殊的性质,应该能够开发联想.
15.△ABC中,∠A、∠B、∠C的对边分别是a、b、c,AB=8,BC=15,CA=17,则下列结论不正确的是( )
A.△ABC是直角三角形,且AC为斜边 B.△ABC是直角三角形,且∠ABC=90°
C.△ABC的面积是60 D.△ABC是直角三角形,且∠A=60°
答案:D
解答:由题意,所以A、B正确,,故C正确,故不正确的选项是D.
分析:如果不能运用三角函数判断角A的大小,也可以利用单选题的排除法求解此题.
二、填空题(共5小题)
16、斜边的边长为17cm,一条直角边长为8cm的直角三角形的面积是 .
答案:60cm2
解答:由题意,此三角形的另一条直角边为(cm),所以面积为(cm2).
分析:由勾股定理求出直角三角形的另一边长,由面积公式求出直角三角形的面积.
17.一个直角三角形的三边长的平方和为200,则斜边长为 .
答案:10
解答:设直角三角形的三边为、、,则由勾股定理,由题意,所以,所以.
分析:利用代数式列出勾股定理的表达式,并正确求解.
18.一个三角形的三边之比为5∶12∶13,它的周长为60,则它的面积是 .
答案:120
解答:设三角形三边为,,,由题意,解之得,则三角形的三边国10,24,26,因为,所以此三角形为直角三角形,所以它的面积是.
分析:利用比的关系列出三边的代数式,求解三边,判断三角形的形状,并根据形状求出其面积.
19.在Rt△ABC中,斜边AB=4,则AB2+BC2+AC2=_____.
答案:32
解答:由勾股定理,所以.
分析:由勾股定理列出所求代数式关于斜边的关系式,从而直接求解.
20.一长方形的一边长为3cm,面积为12cm2,那么它的一条对角线长是 .
答案:5cm
解答:此长方形的另一边长为,则其一条对角线长为
分析:在长方形中,充分应用垂直关系构造直角三角形,并用勾股定理求解.
三、解答题(共5小题)
21.小明将一幅三角板如图所示摆放在一起,发现只要知道其中一边的长就可以求出其它各边的长,若已知,求的长.
答案:
解答:BC=BD+CD=2CD=8,设AC=x,则AB=x,由勾股定理得()+8=x,解之得x=.
分析:运用勾股定理求解三角板的边长是典型的特殊直角三角形的应用,学生应牢固掌握.
22.如图,∠OAB=∠OBC=∠OCD=90°, AB=BC=CD=1,OA=2,求OD2.
答案:7
解答:因为∠OAB=∠OBC=∠OCD=90°,所以,所以,所以.
分析:反复利用垂直确定直角三角形,并利用勾股定理求解直角三角形的斜边.
23.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形边长是7cm,则正方形A、B、C、D的面积和是多少?
答案:49cm2
解答:由题意,正方形A、B、C、D的面积和等于最大正方形的边长的平方,所以为cm2.
分析:利用正方形各边长相等,并反复利用直角三角形勾股定理,推出正方形A、B、C、D的面积和的公式,运用结论求解.
24.已知等腰三角形ABC的腰长为13cm,另一边长是10cm,由顶点作高AD.
求:(1)高AD的长;
答案:12cm
解答:因为BC=10,所以BD=5,所以在直角三角形ABD中,;
(2)△ABC的面积
答案: 60cm2
解答:
分析:利用等腰三角形三线合一,得到直角三角形,并应用勾股定理求解各边及面积.
25.如图,将长为13米的梯子AC斜靠在墙上,BC长为5米,求梯子顶端A到墙的底边的垂直距离AB.
答案:12米
解答:在直角三角形ABC中,.
分析:运用勾股定理求解有垂直关系的实际问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 8 页 (共 8 页) 版权所有@21世纪教育网
华师大版八年级上册第14章第1节14.1.1直角三角形三边的关系课时练习
一、单选题(共15小题)
1.下列说法正确的是( )
A.若 a、b、c是△ABC的三边,则a2+b2=c2
B.若 a、b、c是Rt△ABC的三边,则a2+b2=c2
C.若 a、b、c是Rt△ABC的三边, ,则a2+b2=c2
D.若 a、b、c是Rt△ABC的三边, ,则a2+b2=c2
答案:D
解答:两直角边的平方和等于斜边的平方,所以D正确.
分析:利用勾股定理正确书写三角形三边关系的关键是看清谁是直角.
2.Rt△ABC的三条边长分别是、、,则下列各式成立的是( )
A. B. C. D.
答案:B
解答:由三角形三边关系得B正确,A、C错误,因为没有确定哪个角是直角,所以D不一定正确.
分析:本题考察三角形的三边关系和勾股定理.
3.如果直角三角形的两直角边长分别为k2-1,2k(k >1),那么它的斜边长是( )
A.2k B.k+1 C.k2-1 D.k2+1
答案:D
解答:由勾股定理,斜边长为
分析:能运用勾股定理解决有字母的代数式问题.
4.已知a,b,c为△ABC三边,且满足(a2-b2)(a2+b2-c2)=0,则它的形状为( )
A.直角三角形 B.等腰三角形
C.等腰直角三角形 D.等腰三角形或直角三角形
答案:D
解答:由关系式得或,因为,所以或,所以三角形的形状为等腰三角形或直角三角形.
分析:综合分析解析式得到的结论,并判断三角形的形状.
5.直角三角形中一直角边的长为9,另两边为连续自然数,则直角三角形的周长为( )
A.121 B.120 C.90 D.不能确定
答案:C
解答:设直角三角形的另一条直角边为,则斜边为,由勾股定理得,解之得,则其周长为,故选C.
分析:能够运用代数式求解勾股定理产生的方程,并得出正确结论.
6.△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长为( )
A.42 B.32 C.42 或 32 D.37 或 33
答案:C
解答:当高AD是在三角形的内部时,BD=,CD=,所以,所以△ABC的周长为15+13+14=42;当高AD是在三角形的外部时,BC=,所以△ABC的周长为15+13+4=32,故选C.
分析:能够分情况讨论问题是培养学生思辨能力的基本方法.
7.如图小方格都是边长为1的正方形,则四边形ABCD的面积是 ( )
A. 25 B. 12.5 C. 9 D. 8.5
答案:B
解答:四边形ABCD的面积=三角形ACD的面积+三角形ABC的面积=×AC×2+×AC×3=×AC×5=×5×5=12.5,故选B.
分析:正确应用三角形面积公式结合勾股定理求解不规则四边形面积,注意应用面积的割补法.
8.在平面直角坐标系中,已知点P的坐标是(3,4),则OP的长为( ) A.3 B.4 C.5 D.
答案:C
解答:
分析:利用平面直角坐标系,点的坐标的垂直特征,求解直角三角形的斜边.
9.若△ABC中,AB=25cm,AC=26cm,高AD=24,则BC的长为( )
A.17 B.3 C.17或3 D.以上都不对
答案:C
解答:当高AD是在三角形的内部时,BD=,CD=,所以,;当高AD是在三角形的外部时,BC=,故选C.
分析:三角形的高把三角形分为两个直角三角形,这个高可能在三角形的内部或在外部,分情况讨论求解,是培养学生矛盾的两面性的逻辑思维的方法.
10.已知a、b、c是三角形的三边长,如果满足则三角形的
形状是( )
A.底与边不相等的等腰三角形 B.等边三角形
C.钝角三角形 D.直角三角形
答案:D
解答:由题意,,,,所以,,,所以,所以三角形是直角三角形.
分析:由非负和为零,确定、、的值,并用勾股定理的逆定理判断三角形的形状.
11.下列各组数中,能构成直角三角形的是( )
A.4,5,6 B.1,1, C.6,8,11 D.5,12,23
答案:B
解答:符合的三角形是直角三角形,题目当中只有B符合此关系式,故选B.
分析:利用判断直角三角形的方法,即勾股定理的逆定理进行判断.
12.在Rt△ABC中,∠C=90°,a=12,b=16,则c的长为( )
A.26 B.18 C.20 D.21
答案:C
解答:由勾股定理,,故选C.
分析:运用勾股定理进行计算.
13.等边三角形的边长为2,则该三角形的面积为( )
A. B. C. D.3
答案:B
解答:等边三角形的高为,面积为,故选B.
分析:利用等边三角形三线合一,构造直角三角形,并用勾股定理求出高长,最后求出面积.
14.在Rt△ABC中,∠C=90°,∠B=45°,c=10,则a的长为( )
A.5 B. C. D.
答案:C
解答:由题意,则,所以,所以,故选C.
分析:关于特殊的直角三角形,如等腰直角三角形有特殊的性质,应该能够开发联想.
15.△ABC中,∠A、∠B、∠C的对边分别是a、b、c,AB=8,BC=15,CA=17,则下列结论不正确的是( )
A.△ABC是直角三角形,且AC为斜边 B.△ABC是直角三角形,且∠ABC=90°
C.△ABC的面积是60 D.△ABC是直角三角形,且∠A=60°
答案:D
解答:由题意,所以A、B正确,,故C正确,故不正确的选项是D.
分析:如果不能运用三角函数判断角A的大小,也可以利用单选题的排除法求解此题.
二、填空题(共5小题)
16、斜边的边长为17cm,一条直角边长为8cm的直角三角形的面积是 .
答案:60cm2
解答:由题意,此三角形的另一条直角边为(cm),所以面积为(cm2).
分析:由勾股定理求出直角三角形的另一边长,由面积公式求出直角三角形的面积.
17.一个直角三角形的三边长的平方和为200,则斜边长为 .
答案:10
解答:设直角三角形的三边为、、,则由勾股定理,由题意,所以,所以.
分析:利用代数式列出勾股定理的表达式,并正确求解.
18.一个三角形的三边之比为5∶12∶13,它的周长为60,则它的面积是 .
答案:120
解答:设三角形三边为,,,由题意,解之得,则三角形的三边国10,24,26,因为,所以此三角形为直角三角形,所以它的面积是.
分析:利用比的关系列出三边的代数式,求解三边,判断三角形的形状,并根据形状求出其面积.
19.在Rt△ABC中,斜边AB=4,则AB2+BC2+AC2=_____.
答案:32
解答:由勾股定理,所以.
分析:由勾股定理列出所求代数式关于斜边的关系式,从而直接求解.
20.一长方形的一边长为3cm,面积为12cm2,那么它的一条对角线长是 .
答案:5cm
解答:此长方形的另一边长为,则其一条对角线长为
分析:在长方形中,充分应用垂直关系构造直角三角形,并用勾股定理求解.
三、解答题(共5小题)
21.小明将一幅三角板如图所示摆放在一起,发现只要知道其中一边的长就可以求出其它各边的长,若已知,求的长.
答案:
解答:BC=BD+CD=2CD=8,设AC=x,则AB=x,由勾股定理得()+8=x,解之得x=.
分析:运用勾股定理求解三角板的边长是典型的特殊直角三角形的应用,学生应牢固掌握.
22.如图,∠OAB=∠OBC=∠OCD=90°, AB=BC=CD=1,OA=2,求OD2.
答案:7
解答:因为∠OAB=∠OBC=∠OCD=90°,所以,所以,所以.
分析:反复利用垂直确定直角三角形,并利用勾股定理求解直角三角形的斜边.
23.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形边长是7cm,则正方形A、B、C、D的面积和是多少?
答案:49cm2
解答:由题意,正方形A、B、C、D的面积和等于最大正方形的边长的平方,所以为cm2.
分析:利用正方形各边长相等,并反复利用直角三角形勾股定理,推出正方形A、B、C、D的面积和的公式,运用结论求解.
24.已知等腰三角形ABC的腰长为13cm,另一边长是10cm,由顶点作高AD.
求:(1)高AD的长;
答案:12cm
解答:因为BC=10,所以BD=5,所以在直角三角形ABD中,;
(2)△ABC的面积
答案: 60cm2
解答:
分析:利用等腰三角形三线合一,得到直角三角形,并应用勾股定理求解各边及面积.
25.如图,将长为13米的梯子AC斜靠在墙上,BC长为5米,求梯子顶端A到墙的底边的垂直距离AB.
答案:12米
解答:在直角三角形ABC中,.
分析:运用勾股定理求解有垂直关系的实际问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 8 页 (共 8 页) 版权所有@21世纪教育网
