华师大八年级上册第14章14.1勾股定理3反证法
文档属性
| 名称 | 华师大八年级上册第14章14.1勾股定理3反证法 |

|
|
| 格式 | doc | ||
| 文件大小 | 237.5KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-21 17:13:50 | ||
图片预览


文档简介
登陆21世纪教育 助您教考全无忧
华师大版八年级上册第14章第1节14.1.3反证法课时练习
一、单选题(共15小题)
1、用反证法证明一个命题时,下列说法正确的是( )
A.将结论与条件同时否定,推出矛盾
B.肯定条件,否定结论,推出矛盾
C.将被否定的结论当条件,经过推理得出的结论只与原题条件矛盾,才是反证法的正确运用
D.将被否定的结论当条件,原题的条件不能当条件
答案:B
解答:反证法的证明过程是首先假设某命题不成立(即在原命题的题设下,结论不成立),然后推理出明显矛盾的结果,从而下结论说原假设不成立,原命题得证,故选B.
分析:明确反证法的过程是一个否定结论、推出矛盾的过程.
2.否定“自然数a、b、c中恰有一个偶数”时的正确反证假设为( )
A.a、b、c都是奇数 B.a、b、c或都是奇数或至少有两个偶数
C.a、b、c都是偶数 D.a、b、c中至少有两个偶数
答案:B
解答:、、三个数的奇偶性有以下几种情况(1)全是奇数(2)有两个奇数一个偶数(3)有一个奇数两个偶数(4)全是偶数,所以命题的否定应包含(1)、(3)、(4),故选B.
分析:反证法否定结论后得到的结论的相反面,要包括各种相反的情况,不能有漏缺,适应于矛盾的排中律.
3.用反证法证明命题“三角形的内角中至少有一个不大于60°”时,反证假设正确的是( )
A.假设三内角都不大于60° B.假设三内角都大于60°
C.假设三内角至多有一个大于60° D.假设三内角至多有两个大于60°
答案:B
解答:否定结论“三角形的内角中至少有一个不大于60°”,即“三角形的内角全都大于60°”,故选B.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )分析:运用反证法证明时要求学生掌握什么是结论表述的概念,什么是概念的全部,什么是结论表述的概念的相反面,并注意字句的推敲,其思想适用于逻辑和哲学的通用原理.
4.设a,b,c都小于零,则三数a+,c+,b+中( )
A.都不大于-2 B.都不小于-2
C.至少有一个不大于-2 D.至少有一个不小于-2
答案:C
解答:假设三个数,都大于-2,则
,
而,
故与矛盾,假设不成立,这三个数中至少有一个数不大于,故选C.
分析:用反证法证明时首先假设结论不成立,从而推导出与已知条件或公理、定理、定义相矛盾的事实,从而假设不成立,结论正确.
5.“aA.a≠b B.a>b C.a=b D.a=b或a>b
答案:D
解答:与的关系共有三种,即,,,所以的反面是或,故选D.
分析:运用反证法时应弄清与所有的大小关系,找出对立面.
6.用反证法证明“三角形的三个外角中至少有两个钝角”时,应假设( )
A.假设三个外角都是锐角
B.假设至少有一个钝角
C.假设三个外角都是钝角
D.假设三个外角中只有一个钝角
答案:D
解答:“至少有两个”的反面是“至多有一个”,所以应假设三角形的三个外角至多有一个钝角,其含义也可以表述为“三个外角中只有一个钝角”,故选D.
分析:确定反证法习惯用语“至少有个”的反面是“至多有个”,其逻辑思想可以证明,在选择题当中可以直接运用此结论,另外注意同意句的汉语言不同表述.
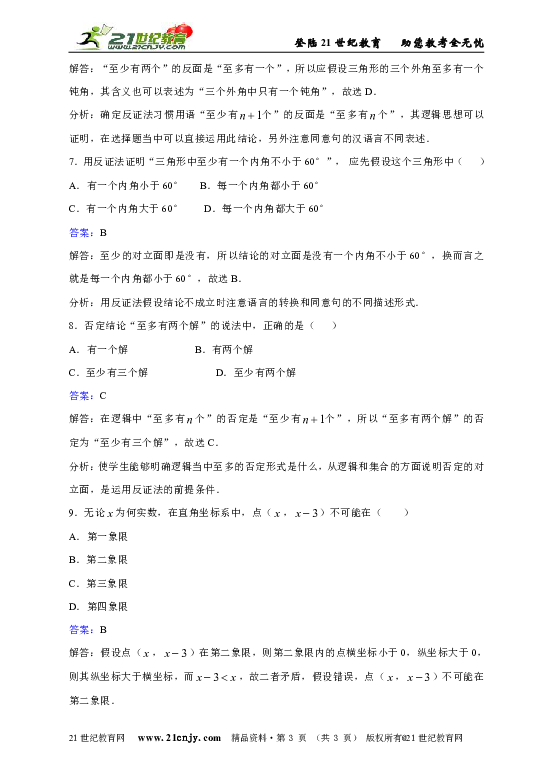
7.用反证法证明“三角形中至少有一个内角不小于60°”,应先假设这个三角形中( ) A.有一个内角小于60° B.每一个内角都小于60°
C.有一个内角大于60° D.每一个内角都大于60°
答案:B
解答:至少的对立面即是没有,所以结论的对立面是没有一个内角不小于60°,换而言之就是每一个内角都小于60°,故选B.
分析:用反证法假设结论不成立时注意语言的转换和同意句的不同描述形式.
8.否定结论“至多有两个解”的说法中,正确的是( )
A.有一个解 B.有两个解
C.至少有三个解 D.至少有两个解
答案:C
解答:在逻辑中“至多有个”的否定是“至少有个”,所以“至多有两个解”的否定为“至少有三个解”,故选C.
分析:使学生能够明确逻辑当中至多的否定形式是什么,从逻辑和集合的方面说明否定的对立面,是运用反证法的前提条件.
9.无论为何实数,在直角坐标系中,点(,)不可能在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
答案:B
解答:假设点(,)在第二象限,则第二象限内的点横坐标小于0,纵坐标大于0,则其纵坐标大于横坐标,而,故二者矛盾,假设错误,点(,)不可能在第二象限.
分析:运用反证法可以解答用直接证明较为困难的题目,反证法为学生的解题提供了新的思维方式.
10. 用反证法证明命题“自然数、、中至少有一个是偶数”,下列假设正确的是( ).
A.假设、、都是偶数
B.假设、、都不是偶数
C.假设、、至多有一个偶数
D.假设、、至多有两个偶数
答案:B
解答:“至少有一个”的反设词应为“没有一个”,故应假设、、都不是偶数,故选B.
分析:学生应有辨析“至少”的意义为“有一个或一个以上”,其对立面即为“没有一个”的能力,做好假设,正确运用反证法.
11. 命题“中,若,则”的结论的否定应该是( )
A.
B.
C.
D.
答案:B
解答:“”的否定应为“”或“”,综合为“”,故选B.
分析:否定应包含概念的所有否定,注意细节及等号的特殊情况.
12.有甲、乙、丙、丁四位歌手参加比赛,其中只有一位获奖,有人走访了四位歌手,甲说:“是乙或丙获奖”,乙说:“甲、丙都未获奖”,丙说:“我获奖了”,丁说:“是乙获奖了”,四位歌手的话只有两句是对的,则获奖的歌手是( )
A.甲 B.乙
C.丙 D.丁
答案:C
解答:因为只有一人获奖,所以丙、丁只有一人说对了,同时甲、乙中只有一人说对了,假设乙说的对,这样丙就错了,丁就对了,也就是甲也对了,与甲错矛盾了,所以乙说错了,从而知甲、丙对,丙是获奖歌手,故选C.
分析:学生应能根据题意进行逻辑假设和逻辑判断,运用反证法的知识进行正确推理.
13. 用反证法证明“是无理数”,最恰当的证法是先假设( )
A.是分数
B.是整数
C.是有理数
D.是实数
答案:C
解答:实数可以分为有理数和无理数,无理数的对立面即是有理数,故选C.
分析:学生应能运用数的分类的知识,把实数分有两大类,无理数的对立面即为有理数,充分运用反证法假设.
14.用反证法证明命题“若,,则时”,应先假设( )
A.不垂直于
B.、都不垂直于
C.
D.与相交
答案:D
解答:在同一平面内,两条直线的位置关系只有两种,即平行或相交,则与平行的否定为与相交,故选D.
分析:学生应结合平面几何的知识分清同一平面内直线的两种位置关系,并找到题设的否定形式.
15.用反证法证明命题“若,则”的第一步是( ).
A.假设
B.假设
C.假设
D.假设
答案:A
解答:用反证法证明时,第一点应是假设命题不成立,即先找到“”的反面,而“”的反面即是“”,故选A.
分析:学生学习了反证法之后,应能够掌握反证法证明的几个关键步骤,并正确解决用直接证明方法较难证明的数学或逻辑问题,反证法应成为培养学生发散思维和逻辑能力的一个有效手段.
二、填空题(共5小题)
16.用反证法证明命题“在一个三角形中,如果两条边不相等,那么它们所对的角也不相等”时,应假设 .
答案:它们所对的角相等
解答:两个角的大小关系有相等和不相等两种可以涵盖所有关系,不相等的对立面即是相等.
分析:根据题意找出结论的对立面,注意要涵盖所有范畴,做出假设.
17.用反证法证明“若│a│<2,则a2<4”时,应假设__________.
答案:
解答:和4的关系只有三种,即,,,故的对立面是.
分析:用反证法要分清结论所包含的所有关系,找出结论的对立面,不能缺失一部分.
18.若用反证法证明命题“在直角三角形中,至少有一个锐角不大于45°”时,
应假设 .
答案:在直角三角形中,两个锐角都大于45°
解答:至少的反面是没有,没有和不大于构成双重否定,即肯定,即两个锐角都大于45°.
分析:运用反证法时注意语言的准确分析,可以运用否定之否定等逻辑进行语言的重新整合.
19.命题“任意多面体的面至少有一个是三角形或四边形或五边形”的结论的否定是 .
答案:没有一个是三角形或四边形或五边形
解答:“至少有一个”的反面即是“没有一个”,所以答案是“没有一个是三角形或四边形或五边形”.
分析:学生应能根据题意正确找出命题结论的对立面,熟悉反证法用语习惯.
20.用反证法证明命题“、都是自然数,可被5整除,那么、中至少有一个能被5整除”,那么反设的内容是 .
答案:、都不能被5整除
解答:“至少”的否定即是“没有一个”,故答案为“、都不能被5整除”.
分析:学生应更多熟悉反证法的逻辑规律和常用语,明晰逻辑条理,正确运用反证法.
三、解答题(共5小题)
21.在△ABC中,已知AB=c,BC=a,CA=b,且∠C≠90°.
求证:a2+b2≠c2
答案:证明:假设在三角形ABC中,,则由勾股定理的逆定理,三角形ABC为直角三角形,且∠C=90°,与已知∠C≠90°矛盾,故假设不成立,三角形ABC中a2+b2≠c2.
分析:运用反证法时要把握好假设命题结论不成立,并且推出矛盾,从而说明假设错误,结论成立.
22.求证两条直线相交只有一个交点.
答案:证明:假设两条直线相交有两个或两个以上的交点,由定理,过两点有且只有一条直线,故与已知两条直线相矛盾,故假设错误,原命题的结论成立,即两条直线相交只有一个交点.
分析:分析题目已知和结论,假设结论不成立,推出与定理相矛盾的关系,从而判断假设错误,原命题成立.
23.求证如果两条直线都与第三条直线平行,那么这两条直线也平行.
答案:证明:假设这两条直线相交,且交点为P,则过P点有两条直线与第三条直线平行,与定理过直线外一点有且只有一条直线与已知直线平行相矛盾,故假设错误,原命题成立,故得证.
分析:熟记已学过的公理、定理、定义,因为它们是推出矛盾的关键.
24.求证:在一个三角形中,如果两个角不等,那么他们所对的边也不等.
答案:证明:假设他们所对的边相等,那么这个三角形是等腰三角形,所以他们所对的角是等腰三角形的两个底角,则这两个角相等,与已知两个角不等矛盾,故假设错误,原命题成立,故得证.
分析:假设结论错误,通过正确的逻辑推理推出矛盾是解决问题的关键.
25.求证:一个三角形中不能有两个直角..
答案:证明:假设三角形中有两个直角,则第三个角的度数为,则不能构成三角形,故假设错误,原命题成立,故得证.
分析:运用反证法推出矛盾可以是多种形式的,只要和公理、定理、定义、已知相矛盾,即可证明假设错误,原命题成立.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 3 页 (共 8 页) 版权所有@21世纪教育网
华师大版八年级上册第14章第1节14.1.3反证法课时练习
一、单选题(共15小题)
1、用反证法证明一个命题时,下列说法正确的是( )
A.将结论与条件同时否定,推出矛盾
B.肯定条件,否定结论,推出矛盾
C.将被否定的结论当条件,经过推理得出的结论只与原题条件矛盾,才是反证法的正确运用
D.将被否定的结论当条件,原题的条件不能当条件
答案:B
解答:反证法的证明过程是首先假设某命题不成立(即在原命题的题设下,结论不成立),然后推理出明显矛盾的结果,从而下结论说原假设不成立,原命题得证,故选B.
分析:明确反证法的过程是一个否定结论、推出矛盾的过程.
2.否定“自然数a、b、c中恰有一个偶数”时的正确反证假设为( )
A.a、b、c都是奇数 B.a、b、c或都是奇数或至少有两个偶数
C.a、b、c都是偶数 D.a、b、c中至少有两个偶数
答案:B
解答:、、三个数的奇偶性有以下几种情况(1)全是奇数(2)有两个奇数一个偶数(3)有一个奇数两个偶数(4)全是偶数,所以命题的否定应包含(1)、(3)、(4),故选B.
分析:反证法否定结论后得到的结论的相反面,要包括各种相反的情况,不能有漏缺,适应于矛盾的排中律.
3.用反证法证明命题“三角形的内角中至少有一个不大于60°”时,反证假设正确的是( )
A.假设三内角都不大于60° B.假设三内角都大于60°
C.假设三内角至多有一个大于60° D.假设三内角至多有两个大于60°
答案:B
解答:否定结论“三角形的内角中至少有一个不大于60°”,即“三角形的内角全都大于60°”,故选B.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )分析:运用反证法证明时要求学生掌握什么是结论表述的概念,什么是概念的全部,什么是结论表述的概念的相反面,并注意字句的推敲,其思想适用于逻辑和哲学的通用原理.
4.设a,b,c都小于零,则三数a+,c+,b+中( )
A.都不大于-2 B.都不小于-2
C.至少有一个不大于-2 D.至少有一个不小于-2
答案:C
解答:假设三个数,都大于-2,则
,
而,
故与矛盾,假设不成立,这三个数中至少有一个数不大于,故选C.
分析:用反证法证明时首先假设结论不成立,从而推导出与已知条件或公理、定理、定义相矛盾的事实,从而假设不成立,结论正确.
5.“a
答案:D
解答:与的关系共有三种,即,,,所以的反面是或,故选D.
分析:运用反证法时应弄清与所有的大小关系,找出对立面.
6.用反证法证明“三角形的三个外角中至少有两个钝角”时,应假设( )
A.假设三个外角都是锐角
B.假设至少有一个钝角
C.假设三个外角都是钝角
D.假设三个外角中只有一个钝角
答案:D
解答:“至少有两个”的反面是“至多有一个”,所以应假设三角形的三个外角至多有一个钝角,其含义也可以表述为“三个外角中只有一个钝角”,故选D.
分析:确定反证法习惯用语“至少有个”的反面是“至多有个”,其逻辑思想可以证明,在选择题当中可以直接运用此结论,另外注意同意句的汉语言不同表述.
7.用反证法证明“三角形中至少有一个内角不小于60°”,应先假设这个三角形中( ) A.有一个内角小于60° B.每一个内角都小于60°
C.有一个内角大于60° D.每一个内角都大于60°
答案:B
解答:至少的对立面即是没有,所以结论的对立面是没有一个内角不小于60°,换而言之就是每一个内角都小于60°,故选B.
分析:用反证法假设结论不成立时注意语言的转换和同意句的不同描述形式.
8.否定结论“至多有两个解”的说法中,正确的是( )
A.有一个解 B.有两个解
C.至少有三个解 D.至少有两个解
答案:C
解答:在逻辑中“至多有个”的否定是“至少有个”,所以“至多有两个解”的否定为“至少有三个解”,故选C.
分析:使学生能够明确逻辑当中至多的否定形式是什么,从逻辑和集合的方面说明否定的对立面,是运用反证法的前提条件.
9.无论为何实数,在直角坐标系中,点(,)不可能在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
答案:B
解答:假设点(,)在第二象限,则第二象限内的点横坐标小于0,纵坐标大于0,则其纵坐标大于横坐标,而,故二者矛盾,假设错误,点(,)不可能在第二象限.
分析:运用反证法可以解答用直接证明较为困难的题目,反证法为学生的解题提供了新的思维方式.
10. 用反证法证明命题“自然数、、中至少有一个是偶数”,下列假设正确的是( ).
A.假设、、都是偶数
B.假设、、都不是偶数
C.假设、、至多有一个偶数
D.假设、、至多有两个偶数
答案:B
解答:“至少有一个”的反设词应为“没有一个”,故应假设、、都不是偶数,故选B.
分析:学生应有辨析“至少”的意义为“有一个或一个以上”,其对立面即为“没有一个”的能力,做好假设,正确运用反证法.
11. 命题“中,若,则”的结论的否定应该是( )
A.
B.
C.
D.
答案:B
解答:“”的否定应为“”或“”,综合为“”,故选B.
分析:否定应包含概念的所有否定,注意细节及等号的特殊情况.
12.有甲、乙、丙、丁四位歌手参加比赛,其中只有一位获奖,有人走访了四位歌手,甲说:“是乙或丙获奖”,乙说:“甲、丙都未获奖”,丙说:“我获奖了”,丁说:“是乙获奖了”,四位歌手的话只有两句是对的,则获奖的歌手是( )
A.甲 B.乙
C.丙 D.丁
答案:C
解答:因为只有一人获奖,所以丙、丁只有一人说对了,同时甲、乙中只有一人说对了,假设乙说的对,这样丙就错了,丁就对了,也就是甲也对了,与甲错矛盾了,所以乙说错了,从而知甲、丙对,丙是获奖歌手,故选C.
分析:学生应能根据题意进行逻辑假设和逻辑判断,运用反证法的知识进行正确推理.
13. 用反证法证明“是无理数”,最恰当的证法是先假设( )
A.是分数
B.是整数
C.是有理数
D.是实数
答案:C
解答:实数可以分为有理数和无理数,无理数的对立面即是有理数,故选C.
分析:学生应能运用数的分类的知识,把实数分有两大类,无理数的对立面即为有理数,充分运用反证法假设.
14.用反证法证明命题“若,,则时”,应先假设( )
A.不垂直于
B.、都不垂直于
C.
D.与相交
答案:D
解答:在同一平面内,两条直线的位置关系只有两种,即平行或相交,则与平行的否定为与相交,故选D.
分析:学生应结合平面几何的知识分清同一平面内直线的两种位置关系,并找到题设的否定形式.
15.用反证法证明命题“若,则”的第一步是( ).
A.假设
B.假设
C.假设
D.假设
答案:A
解答:用反证法证明时,第一点应是假设命题不成立,即先找到“”的反面,而“”的反面即是“”,故选A.
分析:学生学习了反证法之后,应能够掌握反证法证明的几个关键步骤,并正确解决用直接证明方法较难证明的数学或逻辑问题,反证法应成为培养学生发散思维和逻辑能力的一个有效手段.
二、填空题(共5小题)
16.用反证法证明命题“在一个三角形中,如果两条边不相等,那么它们所对的角也不相等”时,应假设 .
答案:它们所对的角相等
解答:两个角的大小关系有相等和不相等两种可以涵盖所有关系,不相等的对立面即是相等.
分析:根据题意找出结论的对立面,注意要涵盖所有范畴,做出假设.
17.用反证法证明“若│a│<2,则a2<4”时,应假设__________.
答案:
解答:和4的关系只有三种,即,,,故的对立面是.
分析:用反证法要分清结论所包含的所有关系,找出结论的对立面,不能缺失一部分.
18.若用反证法证明命题“在直角三角形中,至少有一个锐角不大于45°”时,
应假设 .
答案:在直角三角形中,两个锐角都大于45°
解答:至少的反面是没有,没有和不大于构成双重否定,即肯定,即两个锐角都大于45°.
分析:运用反证法时注意语言的准确分析,可以运用否定之否定等逻辑进行语言的重新整合.
19.命题“任意多面体的面至少有一个是三角形或四边形或五边形”的结论的否定是 .
答案:没有一个是三角形或四边形或五边形
解答:“至少有一个”的反面即是“没有一个”,所以答案是“没有一个是三角形或四边形或五边形”.
分析:学生应能根据题意正确找出命题结论的对立面,熟悉反证法用语习惯.
20.用反证法证明命题“、都是自然数,可被5整除,那么、中至少有一个能被5整除”,那么反设的内容是 .
答案:、都不能被5整除
解答:“至少”的否定即是“没有一个”,故答案为“、都不能被5整除”.
分析:学生应更多熟悉反证法的逻辑规律和常用语,明晰逻辑条理,正确运用反证法.
三、解答题(共5小题)
21.在△ABC中,已知AB=c,BC=a,CA=b,且∠C≠90°.
求证:a2+b2≠c2
答案:证明:假设在三角形ABC中,,则由勾股定理的逆定理,三角形ABC为直角三角形,且∠C=90°,与已知∠C≠90°矛盾,故假设不成立,三角形ABC中a2+b2≠c2.
分析:运用反证法时要把握好假设命题结论不成立,并且推出矛盾,从而说明假设错误,结论成立.
22.求证两条直线相交只有一个交点.
答案:证明:假设两条直线相交有两个或两个以上的交点,由定理,过两点有且只有一条直线,故与已知两条直线相矛盾,故假设错误,原命题的结论成立,即两条直线相交只有一个交点.
分析:分析题目已知和结论,假设结论不成立,推出与定理相矛盾的关系,从而判断假设错误,原命题成立.
23.求证如果两条直线都与第三条直线平行,那么这两条直线也平行.
答案:证明:假设这两条直线相交,且交点为P,则过P点有两条直线与第三条直线平行,与定理过直线外一点有且只有一条直线与已知直线平行相矛盾,故假设错误,原命题成立,故得证.
分析:熟记已学过的公理、定理、定义,因为它们是推出矛盾的关键.
24.求证:在一个三角形中,如果两个角不等,那么他们所对的边也不等.
答案:证明:假设他们所对的边相等,那么这个三角形是等腰三角形,所以他们所对的角是等腰三角形的两个底角,则这两个角相等,与已知两个角不等矛盾,故假设错误,原命题成立,故得证.
分析:假设结论错误,通过正确的逻辑推理推出矛盾是解决问题的关键.
25.求证:一个三角形中不能有两个直角..
答案:证明:假设三角形中有两个直角,则第三个角的度数为,则不能构成三角形,故假设错误,原命题成立,故得证.
分析:运用反证法推出矛盾可以是多种形式的,只要和公理、定理、定义、已知相矛盾,即可证明假设错误,原命题成立.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 3 页 (共 8 页) 版权所有@21世纪教育网
