华师大八年级上册第14章14.2勾股定理的应用
文档属性
| 名称 | 华师大八年级上册第14章14.2勾股定理的应用 |

|
|
| 格式 | doc | ||
| 文件大小 | 225.5KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-21 17:15:48 | ||
图片预览


文档简介
登陆21世纪教育 助您教考全无忧
华师大版八年级上册第14章第2节14.2勾股定理的应用课时练习
一、单选题(共15小题)
1.分别以下列四组为一个三角形的三边的长:①6、8、10;②5、12、13;③8、15、17;④7、8、9,其中能构成直角三角形的有( ).
A.4组 B.3组 C.2组 D.1组
答案:B
解答:按照勾股数可知①、②、③可构成直角三角形,故选B.
分析:牢记勾股数,并能灵活应用于解题之中.
2.等腰三角形底边上高是8,周长为32,则这个等腰三角形的面积为( ).
A.56 B.48 C.40 D.30
答案:B
解答:由题意,这个等腰三角形的半周长为16,和底边上的高8构成直角三角形,由勾股数易知腰长为10,底边的一半为6,故其面积为,故选B.
分析:按照等腰三角形的特性将等腰三角形分成两个全等的直角三角形,运用勾股定理求出边长及面积.
3.要从电杆离地面5m处向地面拉一条长为13m的电缆,则地面电缆固定点与电线杆底部的距离应为( )
A.10m B.11m C.12m D.13m
答案:C
解答:13m与5m与所求距离构成直角三角形的三边,由勾股定理及勾股数,易知,所求距离为12m,故选C.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )分析:要求学生能在实际应用问题当中构建直角三角形,并通过勾股定理求解实际问题.
4.一海轮以24n mile/h的速度从港口A出发向东南方向航行,另一海轮以18n mile/h的速度同时从港口A出发向西南方向航行,离开港口2h后,两海轮之间的距离为( ).
A.84n mile B.60n mile C.48n mile D.36 n mile
答案:B
解答:由题意,两海轮的航向构成直角三角形,则2小时后,两海轮的距离为直角三角形的斜边,其距离为(n mile ),故选B.
分析:利用航向方位得到直角三角形,并利用勾股定理求解所求距离.
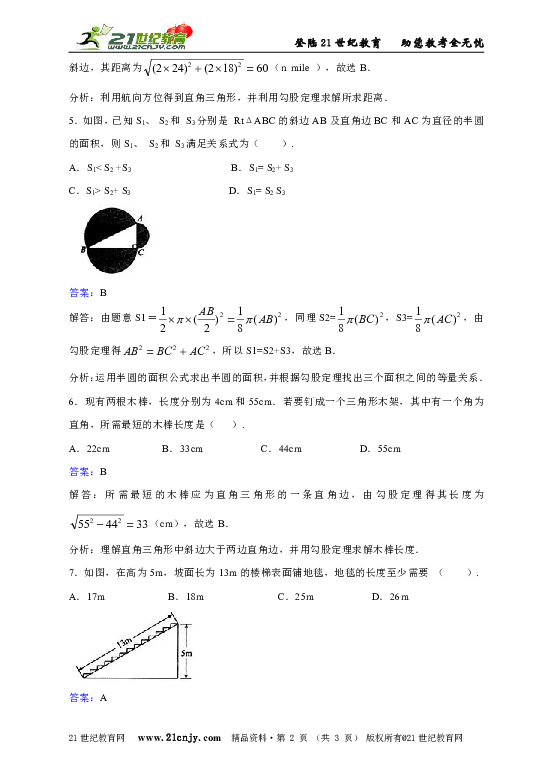
5.如图,已知S1、 S2和 S3分别是 RtΔABC的斜边AB及直角边BC和AC为直径的半圆的面积,则S1、 S2和 S3满足关系式为( ).
A.S1< S2 +S3 B.S1= S2+ S3
C.S1> S2+ S3 D.S1= S2 S3
答案:B
解答:由题意S1=,同理S2=,S3=,由勾股定理得,所以S1=S2+S3,故选B.
分析:运用半圆的面积公式求出半圆的面积,并根据勾股定理找出三个面积之间的等量关系.
6.现有两根木棒,长度分别为4cm和55cm.若要钉成一个三角形木架,其中有一个角为直角,所需最短的木棒长度是( ).
A.22cm B.33cm C.44cm D.55cm
答案:B
解答:所需最短的木棒应为直角三角形的一条直角边,由勾股定理得其长度为(cm),故选B.
分析:理解直角三角形中斜边大于两边直角边,并用勾股定理求解木棒长度.
7.如图,在高为5m,坡面长为13m的楼梯表面铺地毯,地毯的长度至少需要 ( ).
A.17m B.18m C.25m D.26m
答案:A
解答:在所构成的直角三角形中,两直角边分别为5m和(m),地毯的长度展开后为这两条直角边的和5+12=17(m),故选A.
分析:灵活应用勾股定理求解实际问题,并把握实际地毯的铺设方法求出正确的数值.
8.直角三角形的两直角边长分别为3和4,则斜边上的高是( )
A.5 B.1
C. D.
答案:D
解答:由勾股定理,此直角三角形的斜边为5,斜边上的高为,故选D.
分析:先运用勾股定理求出斜边,然后运用面积法求出斜边上的高.
9.三角形的三边长满足,则这个三角形是( )
A.等边三角形
B.钝角三角形
C.直角三角形
D.锐角三角形
答案:C
解答:由,得,即,所以这个三角形是直角三角形.
分析:充分化简关系式,得出勾股定理逆定理的条件,从而判定三角形的形状.
10.如果直角三角形两直角边的比为5:12,则斜边上的高与斜边的比为( ).
A.60:13 B.5:12 C.12:13 D.60:169
答案:D
解答:设直角三角形两直角边为和,由勾股定理得斜边为,则由面积法知斜边上的高为=,则斜边上的高与斜边的比为:=:,故选D.
分析:已知比的关系,应能设比例项,分别求解斜边和斜边上的高,最后消去参数,得到比值.
11. 如果直角三角形的两直角边长分别为,,那么它的斜边长为( )
A. B. C. D.
答案:D
解答:由勾股定理,得斜边长为,故选D.
分析:正确运用勾股定理,并做代数式的化简运算,求出正确答案.
12.已知直角三角形ABC中, ,,,则直角三角形ABC的面积为( )
A.24 B.36
C.48 D.60
答案:A
解答:由题意,此直角三角形的三边满足勾股数6、8、10,故其面积为故选A.
分析:熟记勾股数,并且能够根据题意得出勾股数,算出边长及面积,是学生做选择题的一个快速方法.
13. 已知如图,长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则三角形ABE的面积为( )
A.6cm2 B.8 cm2
C.10cm2 D.12cm2
答案:A
解答:由题意BE=DE,则在直角三角形ABE中,,即,解之得AE=4,所以三角形ABE的面积为(cm2),故选A.
分析:学生应能根据折叠关系找出等量关系,并运用勾股定理求解边长,最后求出面积.
14.如图,在直角三角形ABC中,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
A.2cm B.3cm
C.4cm D.5cm
答案:B
解答:因为直角三角形的两直角边为6cm和8cm,由勾股数知其斜边为10cm,且由折叠关系知CD=DE,则在直角三角形DEB中由勾股定理,得,即为,代入数值得,解之得CD=3cm,故选B.
分析:学生应能根据题意把包含等量关系的数值放入一个直角三角形当中,运用勾股定理列出方程,并正确求解.
15.若三角形ABC的三边、、满足,则三角形ABC的面积为( ).
A.338 B.24
C.26 D.30
答案:D
解答:原式可化,所以,,,满足一组勾股数,所以三角形ABC为直角三角形,其面积为,故选D.
分析:学生应能根据配方法原则进行代数式的整理,化成平方和的形式,从而利用平方的非负性求解三边数值,最后判断三角形是直角三角形,并据此求出三角形ABC的面积.
二、填空题(共5小题)
16.等腰三角形ABC的面积为12cm2,底上的高AD=3cm,则它的周长为 .
答案:18cm
解答:由三角形的面积公式易知,其底边长为=8(cm),底边的一半为4cm,腰长和底边的一半及底上的高构成直角三角形,由勾股数知其腰长为5cm,故其周长为(cm).
分析:利用等腰三角形三线合一,并构建直角三角形,运用勾股定理求解相应边长.
17.轮船在大海中航行,它从A点出发,向正北方向航行20km,遇到冰山后,又折向东航行15km,则此时轮船与A点的距离为 ㎞.
答案:25km
解答:由轮船的航向知正北方向和正东方向构成直角三角形,由勾股定理得此时轮船与A点的距离为(km).
分析:根据方位构建直角三角形,并根据直角三角形勾股定理求距离.
18.如图,为测湖两岸A、B间的距离,小兰在C点设桩,使△ABC为直角三角形,并测得BC=12m,AC=15m,则A、B两点间的距离是 m.
答案:9m
解答:由直角三角形勾股定理可得AB=(m).
分析:利用勾股定理进行间接求解直接法测量不到的边长,这是勾股定理的一个重要应用.
19.如果梯子的底端离建筑物7m,则25m的消防梯可到达建筑物的高度是 m.
答案:24
解答:梯长、梯子底端距离建筑物的距离、可到达建筑物的高度构成直角三角形,由勾股数易知可到达建筑物的高度是24m.
分析:由生活常识探求题目当中包含的直角三角形,并利用勾股数求解.
20.如图,一透明的直圆柱状的玻璃杯,由内部测得其底部半径为3cm,高为8cm,今有一支12cm的吸管任意斜放于杯中,若不考虑吸管的粗细,则吸管露出杯口外的长度至少为 ㎝.
答案:3
解答:由圆柱体的底面直径6㎝和高8㎝构成的直角三角形的斜边是杯中可放吸管的最大长度,由勾股数易知斜边为10㎝,所以吸管露出杯口外的长度至少为13-10=3㎝.
分析:充分利用空间想象能力构建包含最大吸管长度的直角三角形.并用勾股数求解.
三、解答题(共5小题)
21.如图,某人欲横渡一条河,由于水流的影响,实际上岸地点C偏离欲到达点B200m,结果他在水中实际游了520m,求该河流的宽度。
答案:480m
解答:由题意,三角形ABC是直角三角形,且AC=m,BC=200m,则由勾股定理得河流宽度AB=(m).
分析:根据题意构建直角三角形,并用勾股求解题目答案.
22.如图,铁路上A、B两点相距25km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上修建一个土特产收购站E,使得C、D两村到E站的距离相等,则E站应修建在离A站多少千米处?
答案:10 km
解答:由题意知DE=CE,由勾股定理得:,即,解之得AE=10(km).
分析:由等量关系列出关于AE的方程,正确应用勾股定理求解.
23.如图,圆柱的高为10cm,底面半径为2cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,它需要爬行的最短路程是多少厘米?
答案:11.8cm
解答:将圆柱体侧面展开,AB的最短距离为以圆柱体底面半周长和圆柱体的高为两条直角边构成的直角三角形的斜边长,由勾股定理得AB=(cm).
分析:运用空间想象能力,将圆柱体侧面展开图画出来,并构建直角三角形,运用勾股定理求解.
24.在一棵树的10m高处有两只猩猩,其中一只爬下树走向离树20m的池塘,而另一只爬到树顶后直扑池塘。如果两只猩猩经过的距离相等,问这一棵树有多高?
答案:15m
解答:设这一棵树高m,则由题意,整理得,方程两边平方得,化简得,解之得(m).
分析:根据题意,设出未知数,列出相关方程,并正确求解.
25.如下图,根据图上条件,求矩形ABCD的面积.
答案:51cm2
解答:因为直角三角形ADE的两条直角边为15cm和8cm,所以斜边AD=(cm),所以ABCD的面积为=51cm2.
分析:根据题图找出直角三角形,并根据勾股定理求出斜边之长,最后用矩形面积公式求解矩形面积.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 9 页 (共 9 页) 版权所有@21世纪教育网
华师大版八年级上册第14章第2节14.2勾股定理的应用课时练习
一、单选题(共15小题)
1.分别以下列四组为一个三角形的三边的长:①6、8、10;②5、12、13;③8、15、17;④7、8、9,其中能构成直角三角形的有( ).
A.4组 B.3组 C.2组 D.1组
答案:B
解答:按照勾股数可知①、②、③可构成直角三角形,故选B.
分析:牢记勾股数,并能灵活应用于解题之中.
2.等腰三角形底边上高是8,周长为32,则这个等腰三角形的面积为( ).
A.56 B.48 C.40 D.30
答案:B
解答:由题意,这个等腰三角形的半周长为16,和底边上的高8构成直角三角形,由勾股数易知腰长为10,底边的一半为6,故其面积为,故选B.
分析:按照等腰三角形的特性将等腰三角形分成两个全等的直角三角形,运用勾股定理求出边长及面积.
3.要从电杆离地面5m处向地面拉一条长为13m的电缆,则地面电缆固定点与电线杆底部的距离应为( )
A.10m B.11m C.12m D.13m
答案:C
解答:13m与5m与所求距离构成直角三角形的三边,由勾股定理及勾股数,易知,所求距离为12m,故选C.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )分析:要求学生能在实际应用问题当中构建直角三角形,并通过勾股定理求解实际问题.
4.一海轮以24n mile/h的速度从港口A出发向东南方向航行,另一海轮以18n mile/h的速度同时从港口A出发向西南方向航行,离开港口2h后,两海轮之间的距离为( ).
A.84n mile B.60n mile C.48n mile D.36 n mile
答案:B
解答:由题意,两海轮的航向构成直角三角形,则2小时后,两海轮的距离为直角三角形的斜边,其距离为(n mile ),故选B.
分析:利用航向方位得到直角三角形,并利用勾股定理求解所求距离.
5.如图,已知S1、 S2和 S3分别是 RtΔABC的斜边AB及直角边BC和AC为直径的半圆的面积,则S1、 S2和 S3满足关系式为( ).
A.S1< S2 +S3 B.S1= S2+ S3
C.S1> S2+ S3 D.S1= S2 S3
答案:B
解答:由题意S1=,同理S2=,S3=,由勾股定理得,所以S1=S2+S3,故选B.
分析:运用半圆的面积公式求出半圆的面积,并根据勾股定理找出三个面积之间的等量关系.
6.现有两根木棒,长度分别为4cm和55cm.若要钉成一个三角形木架,其中有一个角为直角,所需最短的木棒长度是( ).
A.22cm B.33cm C.44cm D.55cm
答案:B
解答:所需最短的木棒应为直角三角形的一条直角边,由勾股定理得其长度为(cm),故选B.
分析:理解直角三角形中斜边大于两边直角边,并用勾股定理求解木棒长度.
7.如图,在高为5m,坡面长为13m的楼梯表面铺地毯,地毯的长度至少需要 ( ).
A.17m B.18m C.25m D.26m
答案:A
解答:在所构成的直角三角形中,两直角边分别为5m和(m),地毯的长度展开后为这两条直角边的和5+12=17(m),故选A.
分析:灵活应用勾股定理求解实际问题,并把握实际地毯的铺设方法求出正确的数值.
8.直角三角形的两直角边长分别为3和4,则斜边上的高是( )
A.5 B.1
C. D.
答案:D
解答:由勾股定理,此直角三角形的斜边为5,斜边上的高为,故选D.
分析:先运用勾股定理求出斜边,然后运用面积法求出斜边上的高.
9.三角形的三边长满足,则这个三角形是( )
A.等边三角形
B.钝角三角形
C.直角三角形
D.锐角三角形
答案:C
解答:由,得,即,所以这个三角形是直角三角形.
分析:充分化简关系式,得出勾股定理逆定理的条件,从而判定三角形的形状.
10.如果直角三角形两直角边的比为5:12,则斜边上的高与斜边的比为( ).
A.60:13 B.5:12 C.12:13 D.60:169
答案:D
解答:设直角三角形两直角边为和,由勾股定理得斜边为,则由面积法知斜边上的高为=,则斜边上的高与斜边的比为:=:,故选D.
分析:已知比的关系,应能设比例项,分别求解斜边和斜边上的高,最后消去参数,得到比值.
11. 如果直角三角形的两直角边长分别为,,那么它的斜边长为( )
A. B. C. D.
答案:D
解答:由勾股定理,得斜边长为,故选D.
分析:正确运用勾股定理,并做代数式的化简运算,求出正确答案.
12.已知直角三角形ABC中, ,,,则直角三角形ABC的面积为( )
A.24 B.36
C.48 D.60
答案:A
解答:由题意,此直角三角形的三边满足勾股数6、8、10,故其面积为故选A.
分析:熟记勾股数,并且能够根据题意得出勾股数,算出边长及面积,是学生做选择题的一个快速方法.
13. 已知如图,长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则三角形ABE的面积为( )
A.6cm2 B.8 cm2
C.10cm2 D.12cm2
答案:A
解答:由题意BE=DE,则在直角三角形ABE中,,即,解之得AE=4,所以三角形ABE的面积为(cm2),故选A.
分析:学生应能根据折叠关系找出等量关系,并运用勾股定理求解边长,最后求出面积.
14.如图,在直角三角形ABC中,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
A.2cm B.3cm
C.4cm D.5cm
答案:B
解答:因为直角三角形的两直角边为6cm和8cm,由勾股数知其斜边为10cm,且由折叠关系知CD=DE,则在直角三角形DEB中由勾股定理,得,即为,代入数值得,解之得CD=3cm,故选B.
分析:学生应能根据题意把包含等量关系的数值放入一个直角三角形当中,运用勾股定理列出方程,并正确求解.
15.若三角形ABC的三边、、满足,则三角形ABC的面积为( ).
A.338 B.24
C.26 D.30
答案:D
解答:原式可化,所以,,,满足一组勾股数,所以三角形ABC为直角三角形,其面积为,故选D.
分析:学生应能根据配方法原则进行代数式的整理,化成平方和的形式,从而利用平方的非负性求解三边数值,最后判断三角形是直角三角形,并据此求出三角形ABC的面积.
二、填空题(共5小题)
16.等腰三角形ABC的面积为12cm2,底上的高AD=3cm,则它的周长为 .
答案:18cm
解答:由三角形的面积公式易知,其底边长为=8(cm),底边的一半为4cm,腰长和底边的一半及底上的高构成直角三角形,由勾股数知其腰长为5cm,故其周长为(cm).
分析:利用等腰三角形三线合一,并构建直角三角形,运用勾股定理求解相应边长.
17.轮船在大海中航行,它从A点出发,向正北方向航行20km,遇到冰山后,又折向东航行15km,则此时轮船与A点的距离为 ㎞.
答案:25km
解答:由轮船的航向知正北方向和正东方向构成直角三角形,由勾股定理得此时轮船与A点的距离为(km).
分析:根据方位构建直角三角形,并根据直角三角形勾股定理求距离.
18.如图,为测湖两岸A、B间的距离,小兰在C点设桩,使△ABC为直角三角形,并测得BC=12m,AC=15m,则A、B两点间的距离是 m.
答案:9m
解答:由直角三角形勾股定理可得AB=(m).
分析:利用勾股定理进行间接求解直接法测量不到的边长,这是勾股定理的一个重要应用.
19.如果梯子的底端离建筑物7m,则25m的消防梯可到达建筑物的高度是 m.
答案:24
解答:梯长、梯子底端距离建筑物的距离、可到达建筑物的高度构成直角三角形,由勾股数易知可到达建筑物的高度是24m.
分析:由生活常识探求题目当中包含的直角三角形,并利用勾股数求解.
20.如图,一透明的直圆柱状的玻璃杯,由内部测得其底部半径为3cm,高为8cm,今有一支12cm的吸管任意斜放于杯中,若不考虑吸管的粗细,则吸管露出杯口外的长度至少为 ㎝.
答案:3
解答:由圆柱体的底面直径6㎝和高8㎝构成的直角三角形的斜边是杯中可放吸管的最大长度,由勾股数易知斜边为10㎝,所以吸管露出杯口外的长度至少为13-10=3㎝.
分析:充分利用空间想象能力构建包含最大吸管长度的直角三角形.并用勾股数求解.
三、解答题(共5小题)
21.如图,某人欲横渡一条河,由于水流的影响,实际上岸地点C偏离欲到达点B200m,结果他在水中实际游了520m,求该河流的宽度。
答案:480m
解答:由题意,三角形ABC是直角三角形,且AC=m,BC=200m,则由勾股定理得河流宽度AB=(m).
分析:根据题意构建直角三角形,并用勾股求解题目答案.
22.如图,铁路上A、B两点相距25km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上修建一个土特产收购站E,使得C、D两村到E站的距离相等,则E站应修建在离A站多少千米处?
答案:10 km
解答:由题意知DE=CE,由勾股定理得:,即,解之得AE=10(km).
分析:由等量关系列出关于AE的方程,正确应用勾股定理求解.
23.如图,圆柱的高为10cm,底面半径为2cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,它需要爬行的最短路程是多少厘米?
答案:11.8cm
解答:将圆柱体侧面展开,AB的最短距离为以圆柱体底面半周长和圆柱体的高为两条直角边构成的直角三角形的斜边长,由勾股定理得AB=(cm).
分析:运用空间想象能力,将圆柱体侧面展开图画出来,并构建直角三角形,运用勾股定理求解.
24.在一棵树的10m高处有两只猩猩,其中一只爬下树走向离树20m的池塘,而另一只爬到树顶后直扑池塘。如果两只猩猩经过的距离相等,问这一棵树有多高?
答案:15m
解答:设这一棵树高m,则由题意,整理得,方程两边平方得,化简得,解之得(m).
分析:根据题意,设出未知数,列出相关方程,并正确求解.
25.如下图,根据图上条件,求矩形ABCD的面积.
答案:51cm2
解答:因为直角三角形ADE的两条直角边为15cm和8cm,所以斜边AD=(cm),所以ABCD的面积为=51cm2.
分析:根据题图找出直角三角形,并根据勾股定理求出斜边之长,最后用矩形面积公式求解矩形面积.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 9 页 (共 9 页) 版权所有@21世纪教育网
