苏教版五年级数学上册2.6 简单组合图形的面积 课件(共17张PPT)
文档属性
| 名称 | 苏教版五年级数学上册2.6 简单组合图形的面积 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 938.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-06 06:26:08 | ||
图片预览



文档简介
(共17张PPT)
苏教版五年级数学上册
2.6 简单组合图形的面积
学习目标
1、使学生结合生活实际认识组合图形,会把组合图形分解成学过的平面图形并计算出面积。
2、能运用所学知识解决生活中组合图形的实际问题;培养学生认真思考,团结协作的能力。
3、通过找一找、分一分、拼一拼,培养学生识图的能力和综合运用有关知识的能力,能合理地
运用“割”“补”等方法来计算组合图形的面积。
重点:探索并掌握组合图形的面积计算方法。
难点:理解并掌握组合图形的组合及分解方法。
一、复习引入:
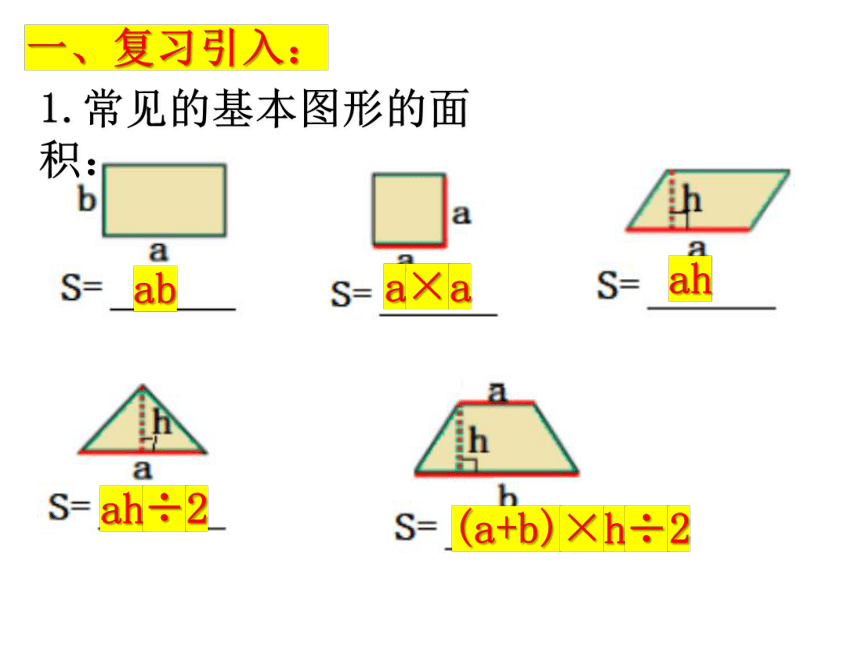
1.常见的基本图形的面积:
ab
a×a
ah
ah÷2
(a+b)×h÷2
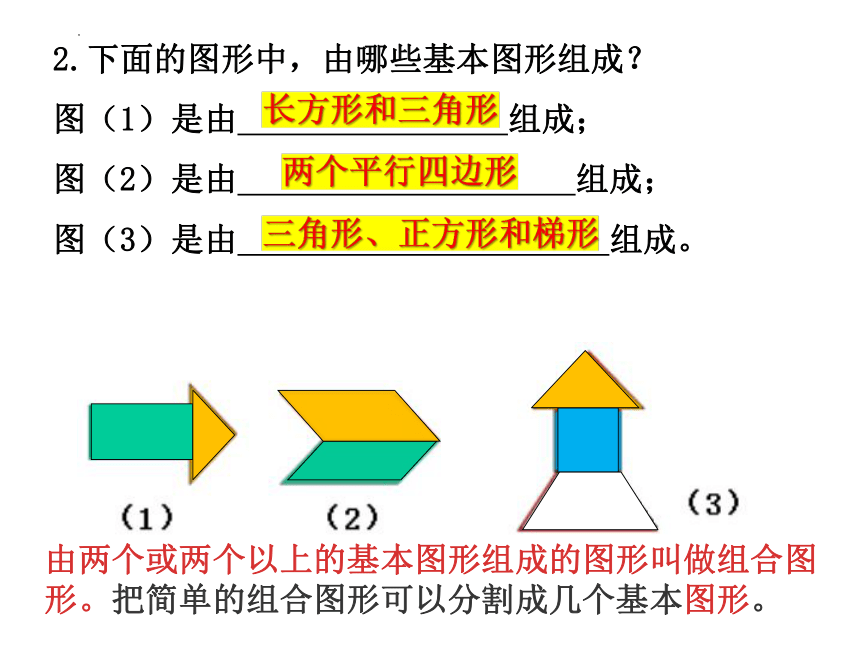
2.下面的图形中,由哪些基本图形组成?
图(1)是由 组成;
图(2)是由 组成;
图(3)是由 组成。
长方形和三角形
两个平行四边形
三角形、正方形和梯形
由两个或两个以上的基本图形组成的图形叫做组合图形。把简单的组合图形可以分割成几个基本图形。
二、探究新知:
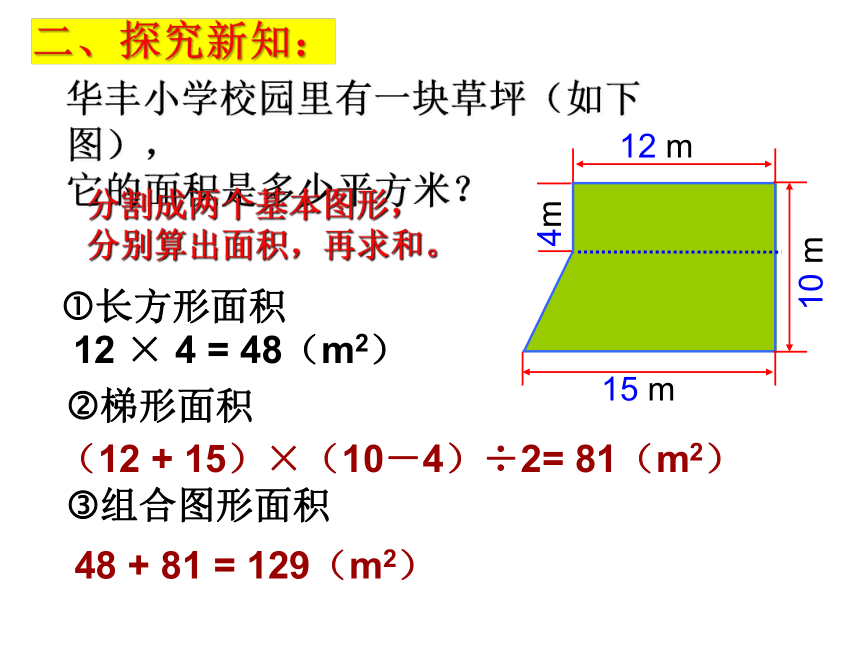
华丰小学校园里有一块草坪(如下图),
它的面积是多少平方米?
12 m
15 m
10 m
4m
分割成两个基本图形,
分别算出面积,再求和。
12 × 4 = 48(m2)
(12 + 15)×(10-4)÷2= 81(m2)
48 + 81 = 129(m2)
长方形面积
梯形面积
组合图形面积
12 m
15 m
10 m
4 m
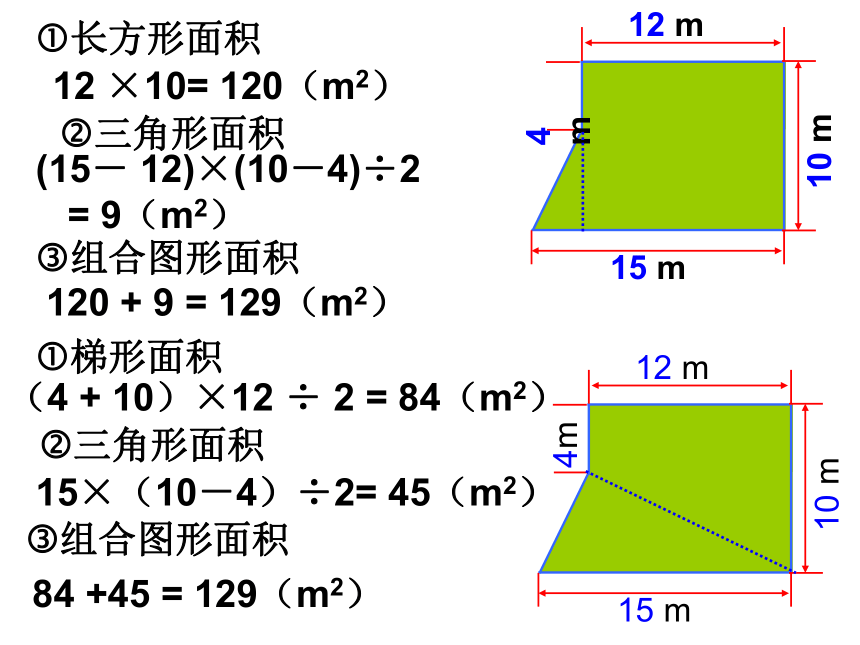
长方形面积
三角形面积
组合图形面积
12 ×10= 120(m2)
(15- 12)×(10-4)÷2
= 9(m2)
120 + 9 = 129(m2)
12 m
15 m
10 m
4m
组合图形面积
梯形面积
三角形面积
(4 + 10)×12 ÷ 2 = 84(m2)
15×(10-4)÷2= 45(m2)
84 +45 = 129(m2)
华丰小学校园里有一块草坪(如下图),
它的面积是多少平方米?
补成一个简单的图形,再去掉补上去的那部分。
12 m
15 m
10 m
4m
长方形面积
梯形面积
组合图形面积
15 ×10= 150(m2)
(4 + 10)×(15-12 )÷ 2 = 21(m2)
150-21 = 129(m2)
归纳:
将一个组合图形分割成几个基本图形,
分别算出面积,再求和。
将一个组合图形添补上一个基本图形,得到
一个大的规则图形,计算大的图形面积与所
补上的图形面积的差。
尝试:
校园里有一个花圃(如图),你能算出它的面积是多少平方米吗?(用两种不同的的割补方法)
6 m
2 m
2 m
5 m
6 m
2 m
2 m
5 m
例题讲解:
例1.计算下面图形的面积。(单位:厘米)
例2、某公园管理员准备靠花圃的矮墙修建一个儿童
乐园(如图)。他用54米长的围栏把这块地围了起来,要洗间的儿童乐园的面积是多少?
三、独立训练
1、计算下图的面积,下列选项中( )方法
与算式80×60-60×20÷2相对应。
2、计算下面图形的面积,列式错误的是( )。
(单位:cm)
A、(12-6)×(10-5)÷2+12×5
B、(5+10)×(12-6)÷2-6×5
C、(5+10)×(12-6)÷2+6×5
D、10×(12-6)÷2+(6+12)×5 ÷2
3、如图,正方形的周长是16厘米,
A和B分别是两条 边的中点。
涂色部分的面积是( )平方厘米。
4、把一张直角梯形的纸按下图这样折叠,
求涂色部分的面积。(单位:cm)
四、拓展提高
如图,大的正方形边长是12dm,小正方形的边长
是6dm,求涂色部分的面积是多少?
五、总结反思
1、计算组合图形的面积的一般步骤:
(1)分析原图能分成哪些基本图形;
(2)寻找求每个基本图形面积需要的数据。
(3)根据公式计算出每个基本图形的面积;
(4)根据关系再(割)相加或(补)相减。
六、随堂检测
1、计算下列组合图形的面积。(单位:米)
2、如图,两个正方形的边长分别是10厘米和6厘米,求阴影部分的面积。
苏教版五年级数学上册
2.6 简单组合图形的面积
学习目标
1、使学生结合生活实际认识组合图形,会把组合图形分解成学过的平面图形并计算出面积。
2、能运用所学知识解决生活中组合图形的实际问题;培养学生认真思考,团结协作的能力。
3、通过找一找、分一分、拼一拼,培养学生识图的能力和综合运用有关知识的能力,能合理地
运用“割”“补”等方法来计算组合图形的面积。
重点:探索并掌握组合图形的面积计算方法。
难点:理解并掌握组合图形的组合及分解方法。
一、复习引入:
1.常见的基本图形的面积:
ab
a×a
ah
ah÷2
(a+b)×h÷2
2.下面的图形中,由哪些基本图形组成?
图(1)是由 组成;
图(2)是由 组成;
图(3)是由 组成。
长方形和三角形
两个平行四边形
三角形、正方形和梯形
由两个或两个以上的基本图形组成的图形叫做组合图形。把简单的组合图形可以分割成几个基本图形。
二、探究新知:
华丰小学校园里有一块草坪(如下图),
它的面积是多少平方米?
12 m
15 m
10 m
4m
分割成两个基本图形,
分别算出面积,再求和。
12 × 4 = 48(m2)
(12 + 15)×(10-4)÷2= 81(m2)
48 + 81 = 129(m2)
长方形面积
梯形面积
组合图形面积
12 m
15 m
10 m
4 m
长方形面积
三角形面积
组合图形面积
12 ×10= 120(m2)
(15- 12)×(10-4)÷2
= 9(m2)
120 + 9 = 129(m2)
12 m
15 m
10 m
4m
组合图形面积
梯形面积
三角形面积
(4 + 10)×12 ÷ 2 = 84(m2)
15×(10-4)÷2= 45(m2)
84 +45 = 129(m2)
华丰小学校园里有一块草坪(如下图),
它的面积是多少平方米?
补成一个简单的图形,再去掉补上去的那部分。
12 m
15 m
10 m
4m
长方形面积
梯形面积
组合图形面积
15 ×10= 150(m2)
(4 + 10)×(15-12 )÷ 2 = 21(m2)
150-21 = 129(m2)
归纳:
将一个组合图形分割成几个基本图形,
分别算出面积,再求和。
将一个组合图形添补上一个基本图形,得到
一个大的规则图形,计算大的图形面积与所
补上的图形面积的差。
尝试:
校园里有一个花圃(如图),你能算出它的面积是多少平方米吗?(用两种不同的的割补方法)
6 m
2 m
2 m
5 m
6 m
2 m
2 m
5 m
例题讲解:
例1.计算下面图形的面积。(单位:厘米)
例2、某公园管理员准备靠花圃的矮墙修建一个儿童
乐园(如图)。他用54米长的围栏把这块地围了起来,要洗间的儿童乐园的面积是多少?
三、独立训练
1、计算下图的面积,下列选项中( )方法
与算式80×60-60×20÷2相对应。
2、计算下面图形的面积,列式错误的是( )。
(单位:cm)
A、(12-6)×(10-5)÷2+12×5
B、(5+10)×(12-6)÷2-6×5
C、(5+10)×(12-6)÷2+6×5
D、10×(12-6)÷2+(6+12)×5 ÷2
3、如图,正方形的周长是16厘米,
A和B分别是两条 边的中点。
涂色部分的面积是( )平方厘米。
4、把一张直角梯形的纸按下图这样折叠,
求涂色部分的面积。(单位:cm)
四、拓展提高
如图,大的正方形边长是12dm,小正方形的边长
是6dm,求涂色部分的面积是多少?
五、总结反思
1、计算组合图形的面积的一般步骤:
(1)分析原图能分成哪些基本图形;
(2)寻找求每个基本图形面积需要的数据。
(3)根据公式计算出每个基本图形的面积;
(4)根据关系再(割)相加或(补)相减。
六、随堂检测
1、计算下列组合图形的面积。(单位:米)
2、如图,两个正方形的边长分别是10厘米和6厘米,求阴影部分的面积。
