湖北省部分高中2024-2025学年高二下学期4月期中联考数学试题(含解析)
文档属性
| 名称 | 湖北省部分高中2024-2025学年高二下学期4月期中联考数学试题(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 776.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-08 00:00:00 | ||
图片预览





文档简介
湖北省部分高中2024 2025学年高二下学期4月期中联考数学试题
一、单选题(本大题共8小题)
1.已知函数,则( )
A. B. C. D.
2.5名同学分别报名参加书法、绘画、摄影、编程四个社团,每个社团至少1人,不同的报名方法有( )
A.种 B.种 C.种 D.种
3.曲线在处的切线方程为( )
A. B. C. D.
4.若,则( )
A. B. C. D.0
5.设,若为函数的极小值点,则( )
A. B. C. D.
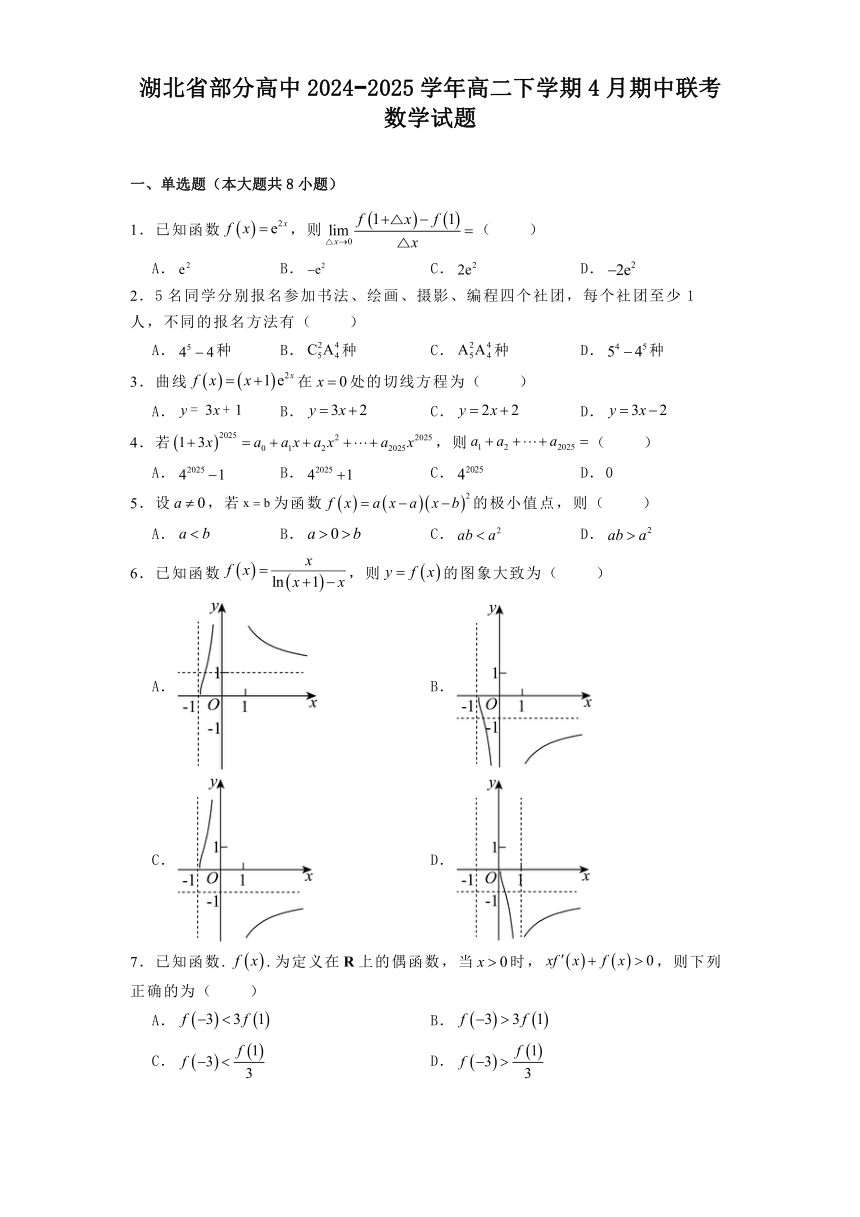
6.已知函数,则的图象大致为( )
A. B.
C. D.
7.已知函数..为定义在上的偶函数,当时,,则下列正确的为( )
A. B.
C. D.
8.已知函数有3个零点,则实数的取值范围为( )
A. B. C. D.
二、多选题(本大题共3小题)
9.下列结论正确的有( )
A.若,则
B.若,则
C.若,则
D.若,则
10.下列说法正确的是( )
A.甲、乙、丙、丁、戊5人站成一排,甲不在最左端,则共有96种排法
B.2名男生和5名女生站成一排,则2名男生相邻的排法共有1280种
C.2名男生和5名女生站成一排,则2名男生互不相邻的排法共有4800种
D.2名男生和5名女生站成一排,2名男生互不相邻且女生甲不能排在最左端的排法共有3120种
11.已知定义在上的函数满足,且当时,.若在上恒成立,则k的可能取值为( )
A.1 B.0 C. D.
三、填空题(本大题共3小题)
12.已知函数在点处的切线方程为,则 .
13.已知,的二项式系数的最大值分别为a,b,若,则正整数 .
14.已知,若对于,不等式恒成立,则的取值范围为 .
四、解答题(本大题共5小题)
15.从装有3个红球、2个白球、1个黑球的袋中任取3个球,求:
(1)恰好取到2个红球的概率;
(2)至少取到1个红球的概率.
16.已知函数,且.
(1)求的解析式;
(2)求函数的单调区间.
17.在的展开式中,
(1)求有理项的个数;
(2)系数最大的项是第几项
18.已知函数.
(1)当时,求在点处的切线方程;
(2)若对,都有恒成立,求的取值范围;
(3)已知,若存在,使得,求证:.
19.已知函数,其中.
(1)若是偶函数,求;
(2)当时,讨论函数在上的零点个数;
(3)若对,求的取值范围.
(注:记,可用含的表达式表示)
参考答案
1.【答案】C
【详解】由,则,
.
故选C.
2.【答案】B
【详解】由题,先将5人分成四组有种,再将四组分配给4个社团有种,
所以不同的报名方法有种.
故选B.
3.【答案】A
【详解】,
则斜率,又,
所以函数在处的切线方程为,即.
故选A.
4.【答案】A
【详解】令,可得,
令,可得,
所以,
故选A.
5.【答案】D
【详解】∵,
∴.
令,解得或.
若,即时,
当时,
令,解得或;令,解得,
∴函数在,上单调递增,在上单调递减,
此时是函数的极大值点,不符合题意;
当时,
令,解得;令,解得或,
∴函数在上单调递增,在,上单调递减,
此时是函数的极小值点,满足题意,
此时由,可得;
若,即时,
当时,
令,解得或;令,解得,
∴函数在,上单调递增,在上单调递减,
此时是函数的极小值点,满足题意,
此时由,可得;
当时,
令,解得;令,解得或,
∴函数在上单调递增,在,上单调递减,
此时是函数的极大值点,不符合题意,
综上,一定成立.
故选D.
6.【答案】C
【详解】由题意可得,解得且,即定义域为,可排除D,
设,则,
所以当时,;当时,,即,
所以当时,,可排除A;当,,可排除A,
综上,C为正确选项.
故选C.
7.【答案】D
【详解】令函数,而函数是偶函数,则,
即函数是奇函数,当时,求导得,
即函数在上递增,则在上递增,
因为,所以,即,
所以,虽然,但不能确定与的大小,故ABC错误,D正确.
故选D.
8.【答案】B
【详解】函数的定义域满足:,解得,
则函数的定义域为:,
,
要使得函数有3个零点,则在有两个变号零点,
令整理得,所以,
解得,故实数的取值范围为.
故选B.
9.【答案】ACD
【详解】对于A,若,则,故选项A正确;
对于B,若,则,故选项B错误;
对于C,若,则,故选项C正确;
对于D,若,则,故选项D正确.
故选ACD.
10.【答案】AD
【详解】对于A:先排最左端,有种排法,再排剩余4个位置,有种排法,则共有种排法,故A正确;
对于B:2名男生相邻,有种排法,和剩余5名女生排列,相当于6人作排列,有种排法,所以共有种排法,故B错误;
对于C:先排5名女生,共有种排法,且形成6个空位,再排2名男生,共有种排法,所以共有种排法,故C错误;
对于D:由C选项可得2名男生和5名女生站成一排,则2名男生互不相邻的排法共有种排法,若女生甲在最左端,且男生互不相邻的排法有种排法,所以2名男生互不相邻且女生甲不能排在最左端的排法共有种,故D正确.
故选AD.
11.【答案】CD
【详解】定义在上的函数满足,则为奇函数,
所以,所以,
则当时,,则恒成立,
所以函数在上单调递增,则函数在上单调递减,
所以在上递增,
不等式转化为:,
所以,即,
因为,所以,则,故
故选CD.
12.【答案】3
【详解】∵,∴,.
∵函数在点处的切线方程为,
∴,,
解得,,∴.
13.【答案】5
【详解】因为为偶数,为奇数,结合二项式系数的最值可得,
又因为,即,
可得,整理可得,解得.
14.【答案】
【详解】不等式,可化为,,
令,则,
所以在上单调递增,
因为,,所以,,则,
所以不等式,即为,
,即对恒成立,
令,则,
当时,,即单调递增,
当时,,即单调递减,
,则,即的取值范围为.
15.【答案】(1)
(2)
【详解】(1)设“恰好取到2个红球”为事件A,则;
(2)设“至少取到1个红球”为事件B,则.
16.【答案】(1)
(2)的单调增区间为,单调减区间.
【详解】(1)由题意知,,
所以,
又,所以,
故函数解析式为.
(2)由(1)知,,
令,得,(舍),
当时,;当时,,
故在上单调递增,在上单调递减.
17.【答案】(1)4个
(2)第8项
【详解】(1)由二项式定理知,
要为有理项则,因为,且,
所以,故有理项有4个;
(2)设第项的系数最大,则
解得,
又,故.
所以系数最大的项为第8项
18.【答案】(1)
(2)
(3)证明见解析
【详解】(1)当时,所以,所以
又,故所求切线方程为,即
(2)方法一:原命题等价于对恒成立,
令,则,
∵,令∴
∴在单调递增,在单调递减
又,,又,所以
故的取值范围为.
方法二:由题意知,当时,,又,
①当时,恒成立,即在上单调递减,
所以恒成立,所以,
②当时,由,得到,由,得到,
所以在区间上单调递减,在区间上单调递增,
当,即时,在区间上单调递增,,
所以,(舍去),
当即时,在上单调递减,,所以
当即时,在区间上单调递减,在区间上单调递增,
所以,得到,所以,
综上,的取值范围为.
(3)∵,令,得
则在单调递减,在单调递增
又且,所以
要证,只需证明,
因为,,且函数在区间上单调递增,
所以只需证明,又因为,即证,
令,
即,注意到,
因为,
则在上单调递减,所以在恒成立,
所以.
19.【答案】(1)
(2)2个
(3)
【详解】(1)由题意可知,即
即,即
则,又,故.
(2)当时,,则,
令,则恒成立,
故在上单调递增,
又,,故使得,
则得;得,
故在单调递减,在单调递增,
又因,则,
又,则在上存在一个零点,
故在上有2个零点.
(3)因对恒成立,
则当时,上式必然成立,此时,又因,则;
当时,,
令,则,
则在上单调递增,则,
(i)若,则,则在上单调递增,
则,符合题意;
(ii)若,则,,
则由零点存在性定理可知,使得,即①,
则得,得,
则在上单调递减,在上单调递增,
则②,
因,,则,
若,②式显然成立,
若,即,
则联立,得,得或(舍),
因,则,即,
则,则,
因,则,则,
则
综上可知,的取值范围是.
一、单选题(本大题共8小题)
1.已知函数,则( )
A. B. C. D.
2.5名同学分别报名参加书法、绘画、摄影、编程四个社团,每个社团至少1人,不同的报名方法有( )
A.种 B.种 C.种 D.种
3.曲线在处的切线方程为( )
A. B. C. D.
4.若,则( )
A. B. C. D.0
5.设,若为函数的极小值点,则( )
A. B. C. D.
6.已知函数,则的图象大致为( )
A. B.
C. D.
7.已知函数..为定义在上的偶函数,当时,,则下列正确的为( )
A. B.
C. D.
8.已知函数有3个零点,则实数的取值范围为( )
A. B. C. D.
二、多选题(本大题共3小题)
9.下列结论正确的有( )
A.若,则
B.若,则
C.若,则
D.若,则
10.下列说法正确的是( )
A.甲、乙、丙、丁、戊5人站成一排,甲不在最左端,则共有96种排法
B.2名男生和5名女生站成一排,则2名男生相邻的排法共有1280种
C.2名男生和5名女生站成一排,则2名男生互不相邻的排法共有4800种
D.2名男生和5名女生站成一排,2名男生互不相邻且女生甲不能排在最左端的排法共有3120种
11.已知定义在上的函数满足,且当时,.若在上恒成立,则k的可能取值为( )
A.1 B.0 C. D.
三、填空题(本大题共3小题)
12.已知函数在点处的切线方程为,则 .
13.已知,的二项式系数的最大值分别为a,b,若,则正整数 .
14.已知,若对于,不等式恒成立,则的取值范围为 .
四、解答题(本大题共5小题)
15.从装有3个红球、2个白球、1个黑球的袋中任取3个球,求:
(1)恰好取到2个红球的概率;
(2)至少取到1个红球的概率.
16.已知函数,且.
(1)求的解析式;
(2)求函数的单调区间.
17.在的展开式中,
(1)求有理项的个数;
(2)系数最大的项是第几项
18.已知函数.
(1)当时,求在点处的切线方程;
(2)若对,都有恒成立,求的取值范围;
(3)已知,若存在,使得,求证:.
19.已知函数,其中.
(1)若是偶函数,求;
(2)当时,讨论函数在上的零点个数;
(3)若对,求的取值范围.
(注:记,可用含的表达式表示)
参考答案
1.【答案】C
【详解】由,则,
.
故选C.
2.【答案】B
【详解】由题,先将5人分成四组有种,再将四组分配给4个社团有种,
所以不同的报名方法有种.
故选B.
3.【答案】A
【详解】,
则斜率,又,
所以函数在处的切线方程为,即.
故选A.
4.【答案】A
【详解】令,可得,
令,可得,
所以,
故选A.
5.【答案】D
【详解】∵,
∴.
令,解得或.
若,即时,
当时,
令,解得或;令,解得,
∴函数在,上单调递增,在上单调递减,
此时是函数的极大值点,不符合题意;
当时,
令,解得;令,解得或,
∴函数在上单调递增,在,上单调递减,
此时是函数的极小值点,满足题意,
此时由,可得;
若,即时,
当时,
令,解得或;令,解得,
∴函数在,上单调递增,在上单调递减,
此时是函数的极小值点,满足题意,
此时由,可得;
当时,
令,解得;令,解得或,
∴函数在上单调递增,在,上单调递减,
此时是函数的极大值点,不符合题意,
综上,一定成立.
故选D.
6.【答案】C
【详解】由题意可得,解得且,即定义域为,可排除D,
设,则,
所以当时,;当时,,即,
所以当时,,可排除A;当,,可排除A,
综上,C为正确选项.
故选C.
7.【答案】D
【详解】令函数,而函数是偶函数,则,
即函数是奇函数,当时,求导得,
即函数在上递增,则在上递增,
因为,所以,即,
所以,虽然,但不能确定与的大小,故ABC错误,D正确.
故选D.
8.【答案】B
【详解】函数的定义域满足:,解得,
则函数的定义域为:,
,
要使得函数有3个零点,则在有两个变号零点,
令整理得,所以,
解得,故实数的取值范围为.
故选B.
9.【答案】ACD
【详解】对于A,若,则,故选项A正确;
对于B,若,则,故选项B错误;
对于C,若,则,故选项C正确;
对于D,若,则,故选项D正确.
故选ACD.
10.【答案】AD
【详解】对于A:先排最左端,有种排法,再排剩余4个位置,有种排法,则共有种排法,故A正确;
对于B:2名男生相邻,有种排法,和剩余5名女生排列,相当于6人作排列,有种排法,所以共有种排法,故B错误;
对于C:先排5名女生,共有种排法,且形成6个空位,再排2名男生,共有种排法,所以共有种排法,故C错误;
对于D:由C选项可得2名男生和5名女生站成一排,则2名男生互不相邻的排法共有种排法,若女生甲在最左端,且男生互不相邻的排法有种排法,所以2名男生互不相邻且女生甲不能排在最左端的排法共有种,故D正确.
故选AD.
11.【答案】CD
【详解】定义在上的函数满足,则为奇函数,
所以,所以,
则当时,,则恒成立,
所以函数在上单调递增,则函数在上单调递减,
所以在上递增,
不等式转化为:,
所以,即,
因为,所以,则,故
故选CD.
12.【答案】3
【详解】∵,∴,.
∵函数在点处的切线方程为,
∴,,
解得,,∴.
13.【答案】5
【详解】因为为偶数,为奇数,结合二项式系数的最值可得,
又因为,即,
可得,整理可得,解得.
14.【答案】
【详解】不等式,可化为,,
令,则,
所以在上单调递增,
因为,,所以,,则,
所以不等式,即为,
,即对恒成立,
令,则,
当时,,即单调递增,
当时,,即单调递减,
,则,即的取值范围为.
15.【答案】(1)
(2)
【详解】(1)设“恰好取到2个红球”为事件A,则;
(2)设“至少取到1个红球”为事件B,则.
16.【答案】(1)
(2)的单调增区间为,单调减区间.
【详解】(1)由题意知,,
所以,
又,所以,
故函数解析式为.
(2)由(1)知,,
令,得,(舍),
当时,;当时,,
故在上单调递增,在上单调递减.
17.【答案】(1)4个
(2)第8项
【详解】(1)由二项式定理知,
要为有理项则,因为,且,
所以,故有理项有4个;
(2)设第项的系数最大,则
解得,
又,故.
所以系数最大的项为第8项
18.【答案】(1)
(2)
(3)证明见解析
【详解】(1)当时,所以,所以
又,故所求切线方程为,即
(2)方法一:原命题等价于对恒成立,
令,则,
∵,令∴
∴在单调递增,在单调递减
又,,又,所以
故的取值范围为.
方法二:由题意知,当时,,又,
①当时,恒成立,即在上单调递减,
所以恒成立,所以,
②当时,由,得到,由,得到,
所以在区间上单调递减,在区间上单调递增,
当,即时,在区间上单调递增,,
所以,(舍去),
当即时,在上单调递减,,所以
当即时,在区间上单调递减,在区间上单调递增,
所以,得到,所以,
综上,的取值范围为.
(3)∵,令,得
则在单调递减,在单调递增
又且,所以
要证,只需证明,
因为,,且函数在区间上单调递增,
所以只需证明,又因为,即证,
令,
即,注意到,
因为,
则在上单调递减,所以在恒成立,
所以.
19.【答案】(1)
(2)2个
(3)
【详解】(1)由题意可知,即
即,即
则,又,故.
(2)当时,,则,
令,则恒成立,
故在上单调递增,
又,,故使得,
则得;得,
故在单调递减,在单调递增,
又因,则,
又,则在上存在一个零点,
故在上有2个零点.
(3)因对恒成立,
则当时,上式必然成立,此时,又因,则;
当时,,
令,则,
则在上单调递增,则,
(i)若,则,则在上单调递增,
则,符合题意;
(ii)若,则,,
则由零点存在性定理可知,使得,即①,
则得,得,
则在上单调递减,在上单调递增,
则②,
因,,则,
若,②式显然成立,
若,即,
则联立,得,得或(舍),
因,则,即,
则,则,
因,则,则,
则
综上可知,的取值范围是.
同课章节目录
