期末测试(含解析)2024-2025学年五年级下册数学苏教版
文档属性
| 名称 | 期末测试(含解析)2024-2025学年五年级下册数学苏教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 277.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-06 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末测试
一、选择题
1.车轮做成圆的,车轴应装在( )。
A.圆心位置 B.圆上任何位置 C.圆内任何位置 D.圆的直径上
2.如果是假分数,那么符合条件的x值有( )个。
A.3 B.4 C.5 D.无数
3.圆周率π是一个( )。
A.近似数 B.两位小数 C.无限不循环小数
4.甲绳比乙绳长米,丙绳比乙绳短米。甲绳与丙绳相比,( )。
A.甲绳长 B.甲绳短 C.一样长 D.无法确定哪根长
5.a、b是两个相邻自然数(a、b都不为0),a和b的最大公因数是( ),最小公倍数是( )。
A.1;ab B.ab;b C.a;ab D.b;b
6.把一个边长为12厘米的正方形铁丝改围成一个长方形,长方形的长是宽的3倍,设宽为厘米,则下列方程中,( )是正确的。
A. B.
C. D.
7.小军要用一张纸片,从中剪下一个面积是16π平方厘米的圆形纸片,应该选择下面的( )纸片。
A.边长是4厘米的正方形
B.长是8厘米,宽是6厘米的长方形
C.周长是28厘米的正方形
D.长是10厘米,宽是8厘米的长方形
8.105名同学参加团体操表演,如果要求每排人数必须相等,并且每排不能少于10人,不能多于30人,符合条件的队列一共有( )种。
A.1 B.2 C.3 D.4
9.算式“1×3×5×…×99×2”的积是( )。
A.质数 B.奇数 C.偶数 D.无法确定
10.一个圆形射击靶的周长是2.826米,射中靶心代表是10环,一个运动员射击时得了4环,他射中的位置距离靶心可能是( )厘米。
A.900 B.90 C.50 D.30
二、填空题
11.在①14-x=8;②7×5=35;③x÷0.9=1.8;④100a;⑤79<83x;⑥15y=6+x中,方程有( ),等式有( )。
12.分数加减混合运算的运算顺序和( )混合运算的运算顺序相同。
13.端午节期间,小明和爸爸去大洋湾观看龙舟赛。入住酒店后,小明问爸爸:“我们的房间号是多少?”爸爸说:“房间号由三个数字组成,第一个数字代表楼层,它既是质数又是偶数;后面两个数字代表房间顺序,它是20以内最大的奇数。”小明和爸爸的房间号是( )。
14.一根a米长的彩带,如果用去它的,还剩下它的 ;如果用去米,还剩下 米。
15.的分数单位是( ),它有( )个这样的分数单位。
16.五年级一班学生中,会打乒乓球的占,这里是把( )看作单位“1”,平均分成了( )份,会打乒乓球的学生占( )份。
17.把一根3米长的木料锯成相等的5小段,每段是这根木料的,是米。
18.在横线上填写最简分数。
18角= 元 18厘米 米 380千克= 吨
42分= 时 125平方分米= 平方米 32平方米= 公顷
19.先把数量关系补充完整,再列出方程。
(1)公交车上原有15人,到站后下车x人,又上车12人,车上现在18人。
数量关系:
方程:
(2)女儿今年x岁,妈妈今年年龄是女儿的3倍,比女儿大30岁。
数量关系:
方程:
20.数形结合是数学上常用的思想方法。观察图中小正方形的数量,其中灰白相间的小正方形的个数依次对应着奇数组成的算式中的每一个数。请你找出其中规律,用最简便的方法计算下面的算式。
(1)( )( )( )
(2)( )( )( )
三、判断题
21.一个圆的半径是3厘米,它的直径是6厘米。( )
22.把60分解质因数是60=2×3×10。( )
23.扇形是由圆的两条半径和一段曲线围成的。( )
24.打开数学书,左右两边页码的积是奇数。( )
25.两个不同的非0自然数的最小公倍数总是大于这两个数的最大公因数。( )
四、计算题
26.解方程。
1.3x-0.44=0.6 x-+2=5 -x=
27.直接写出得数。
五、解答题
28.在一块草地的木柱上拴着一头牛,拴牛的绳长为5米(拴在木桩上的绳子忽略不计),牛最多可吃到草的面积是多少平方米?
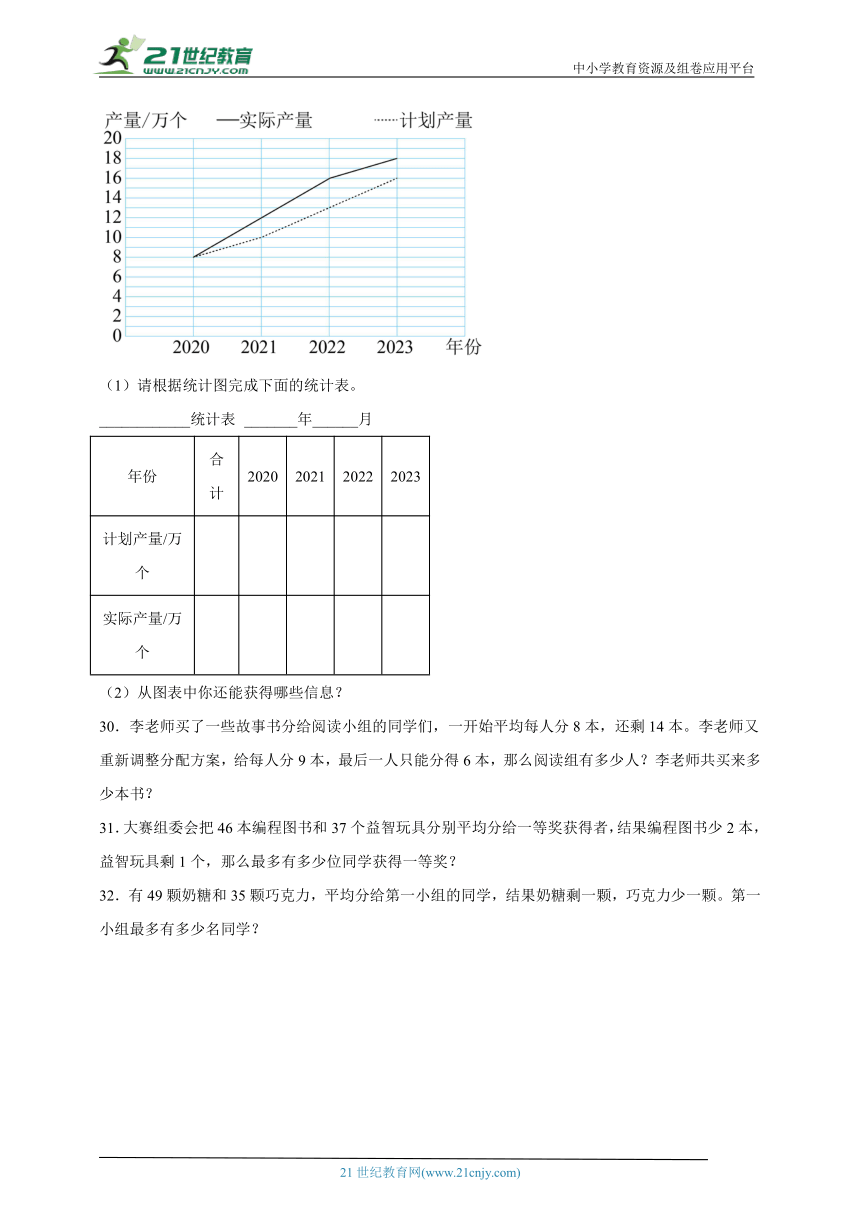
29.下面是某电子厂2020~2023年一种电子元件的产量统计图。
(1)请根据统计图完成下面的统计表。
____________统计表 _______年______月
年份 合计 2020 2021 2022 2023
计划产量/万个
实际产量/万个
(2)从图表中你还能获得哪些信息?
30.李老师买了一些故事书分给阅读小组的同学们,一开始平均每人分8本,还剩14本。李老师又重新调整分配方案,给每人分9本,最后一人只能分得6本,那么阅读组有多少人?李老师共买来多少本书?
31.大赛组委会把46本编程图书和37个益智玩具分别平均分给一等奖获得者,结果编程图书少2本,益智玩具剩1个,那么最多有多少位同学获得一等奖?
32.有49颗奶糖和35颗巧克力,平均分给第一小组的同学,结果奶糖剩一颗,巧克力少一颗。第一小组最多有多少名同学?
《期末测试》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A D C A A D D B C D
1.A
【分析】连接圆心和圆上任意一点的线段叫做半径。半径决定圆的大小,在同一个圆内有无数条半径,同一个圆内所有的半径都相等。
把车轴安装在车轮的圆心处,车开起来更平稳,是利用了同一个圆的半径都相等的特性。
【详解】车轮做成圆的,车轴应装在圆心位置。
故答案为:A
2.D
【分析】分子比分母大或者分子和分母相等的分数叫假分数,据此求解。
【详解】根据假分数的概念,只要,该数就是假分数,所以x的值有无数个。
故答案为:D
【点睛】本题主要考查假分数的概念。
3.C
【分析】圆周率π是圆的周长与直径的比值,在实际应用中,为了便于计算,我们常取π的近似值3.14 ,但实际上它的小数位无穷无尽且不存在循环节。
【详解】A.圆周率π是圆周长与直径的精确比值,并非近似数,只是计算时常用近似值,原题说法错误;
B.π=3.1415926…,小数位无限且无循环规律,不是两位小数,原题说法错误;
C.π小数点后数字无限且无循环节,符合无限不循环小数特征,原题说法正确。
故答案为:C
4.A
【分析】甲绳比乙绳长米,则甲绳的长度>乙绳的长度;丙绳比乙绳短米,则乙绳的长度>丙绳的长度,据此解答。
【详解】甲绳的长度>乙绳的长度,乙绳的长度>丙绳的长度,因此甲绳的长度>乙绳的长度>丙绳的长度,所以甲绳的长度>丙绳的长度,所以甲绳与丙绳相比,甲绳长。
故答案为:A
5.A
【分析】a、b是两个相邻自然数,如2和3,它们是互质数;根据“两个数是互质数时,它们的最大公因数是1,最小公倍数是两数的乘积”进行解答。
公因数只有1的两个非零自然数,叫做互质数。
【详解】a、b是两个相邻自然数(a、b都不为0),则a和b是互质数,a和b的最大公因数是(1),最小公倍数是(ab)。
故答案为:A
6.D
【分析】根据题意,找出数量关系:即正方形的周长等于长方形的周长;由正方形的周长=边长×4,长方形的周长=(长+宽)×2,代入相应数值即可列出方程。
【详解】解:设长方形的宽为厘米,则长方形的长为3x。
因此列出方程正确的是:。
故答案为:D
7.D
【分析】根据题意可知,要在一个长方形纸片上剪一个面积是16π平方厘米的圆,这个长方形的边长等于圆的直径(半径的2倍),首先根据圆的面积公式:S=πr2,已知圆的面积可以求出半径的平方,进而求出半径,然后进行选择即可。
【详解】解:设圆的半径为r厘米
πr2=16π
r2=16
因为4的平方是16,所以圆的半径是4厘米。
这张长方形纸片的长与宽不小于8厘米。
D的长与宽符合题意。
故答案为:D
【点睛】本题主要考查圆的面积公式的灵活运用,关键是熟记公式。
8.B
【分析】根据题意可知,每排人数×排数=总人数,要求每排人数必须相等,说明每排人数是105的因数;先列举出105的所有因数,再从中找出每排不少于10人,不多于30人的因数,即是符合条件的队列。
【详解】105的因数:1,3,5,7,15,21,35,105;
在10~30之间的因数是:15,21;
符合条件的队列是:
①每排15人,共7排;
②每排21人,共5排;
符合条件的队列一共有2种。
故答案为:B
9.C
【分析】奇数:不能被2整除的数是奇数;能被2整除的数是偶数;
质数:除了1和它本身,没有其它因数的数是质数;合数:除了1和它本身,还有其它因数的数是合数;
由于奇数×奇数=奇数,奇数×偶数=偶数,偶数×偶数=偶数,可知在乘法算式里,只有要偶数,那么结果一定是偶数,据此即可选择。
【详解】由分析可知:1×3×5×…×99×2里最后乘了2,2是偶数,所以它的积是偶数。
故答案为:C
10.D
【分析】根据圆的周长公式:C=2πr,计算其半径,再把半径平均分成10份,4环与靶心的距离应该在(10-4)份到(10-3)份之间。
【详解】2.826米=282.6厘米
282.6÷3.14÷2=45(厘米)
45÷10×(10-4)
=45÷10×6
=27(厘米)
45÷10×(10-3)
=45÷10×7
=31.5(厘米)
A.900>31.5,不符合题意;
B.90>31.5,不符合题意;
C.50>31.5,不符合题意;
D.27<30<31.5,符合题意;
他射中的位置距离靶心可能是30厘米。
故答案为:D
【点睛】本题关键是熟练掌握圆的周长公式,明确4环与靶心的距离范围。
11. ①③⑥ ①②③⑥
【分析】含有等号的式子叫等式;含有未知数的等式叫方程。据此判断。
【详解】14-x=8、x÷0.9=1.8、15y=6+x,即含有未知数又是等式,它们是方程。
14-x=8、x÷0.9=1.8、15y=6+x,7×5=35,含有等号,它们是等式。
方程有(①③⑥),等式有(①②③⑥)
【点睛】掌握等式、方程的概念是解答本题的关键。
12.整数
【详解】分数加减混合运算的运算顺序和(整数)混合运算的运算顺序相同。
如:
13.219
【分析】一个数,如果只有1和它本身两个因数,那么这样的数叫做质数;
一个数,如果除了1和它本身还有别的因数,那么这样的数叫做合数;
整数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数。
【详解】第一个数字代表楼层,它既是质数又是偶数,即2;
后面两个数字代表房间顺序,它是20以内最大的奇数,即19;
小明和爸爸的房间号是219。
【点睛】本题考查质数、偶数与奇数的意义及应用,明确2是最小的质数,也是偶数中唯一的质数。
14. a-
【分析】根据题意可知,把这根彩带看作单位“1”,由于用去它的,还剩下它的:1-,算出结果即可;由于用去米,即剩下的米数=总米数-用去的米数,由此即可求解。
【详解】1-=
用去米,还剩下:(a-)米。
【点睛】本题主要考查单位“1”的判断,要注意分数后面加单位表示具体的数。
15. 10
【分析】把单位“1”平均分成若干份取一份的数,叫做分数单位;分数的分子是几里面就有几个这样的分数单位。
【详解】由分析可得:
的分数单位是,的分子是10,所以有10个这样的分数单位。
16. 五年级一班总人数 9 5
【分析】根据分数的意义,由“五年级一班学生中,会打乒乓球的占”知:把五一班全部学生当作单位“1”,平均分成了9份,打乒乓球的点其中的5份。据此解答。
【详解】五年级一班学生中,会打乒乓球的占,这里是把(五年级一班总人数)看作单位“1”,平均分成了(9)份,会打乒乓球的学生占(5)份。
【点睛】此题主要考查了单位“1”的确定及分数的意义。
17.;
【分析】把这根木料的长度看作单位“1”,把它平均锯成5段,每段是总长度的;一根长3米的木料平均锯成5段,求每段长度,用这根木料的长度除以平均锯成的段数;据此解答。
【详解】1÷5=
3÷5=(米)
把一根3米长的木料锯成相等的5小段,每段是这根木料的,是米。
【点睛】解决此题关键是弄清求的是“分率”还是“具体的数量”,求分率:平均分的是单位“1”;求具体的数量:平均分的是具体的数量,要注意:分率不能带单位名称,而具体的数量要带单位名称。
18.
【分析】1元=10角;1米=100厘米;1吨=1000千克;1时=60分;1平方米=100平方分米;1公顷=10000平方米;低级单位换算成高级单位,除以进率;最简分数的意义:分子和分母只有公因数1,像这样的分数叫作最简分数,据此解答。
【详解】18角=元
18厘米=米
380千克=吨
42分=时
125平方分米=平方米
32平方米=时
【点睛】熟记进率以及最简分数的意义是解答本题的关键、
19.(1) 原来车上的人数-下车的人数+上车的人数=此时车上的人数 15-x+12=18
(2) 女儿年龄+30=女儿的年龄×3 x+30=3x
【分析】(1)由于下车的话,人数减少,上车人数增加,那么可知:原来车上的人数-下车的人数+上车的人数=此时车上的人数,据此即可列方程;
(2)由于妈妈今年年龄是女儿的3倍,那么女儿的年龄×3=妈妈的年龄,由于妈妈比女儿大30岁,那么女儿年龄+30=女儿的年龄×3,据此即可列方程。
【详解】(1)由分析可知:
数量关系:原来车上的人数-下车的人数+上车的人数=此时车上的人数
方程:15-x+12=18
(2)数量关系:女儿年龄+30=女儿的年龄×3
方程:x+30=3x
【点睛】本题主要考查列方程,找准等量关系是解题的关键。
20.(1) 100 10 10
(2) 2500 50 50
【分析】根据题干中给出的算式可以得到规律是:差是2,首项是1的等差数列的和等于项数乘项数。
【详解】(1)根据等差数列中项数=(末项+1)÷2可得:
(19+1)÷2
=20÷2
=10
因此。
(2)根据等差数列中项数=(末项+1)÷2可得:
(99+1)÷2
=100÷2
=50
因此。
【点睛】仔细观察给出的算式,找到规律是解决本题的关键。
21.√
【分析】在同一个圆或等圆中,直径是半径的2倍,半径是直径的一半,由此解答问题。
【详解】3×2=6(厘米)
一个圆的半径是3厘米,它的直径是6厘米。原说法正确。
故答案为:√
22.×
【分析】分解质因数是把合数分解成若干个质因数相乘的形式。
【详解】60=2×3×10中10不是质数,把60分解质因数应是60=2×2×3×5。
原题说法错误。
故答案为:×
23.√
【分析】根据扇形的意义:扇形是由圆的两条半径和一段曲线围成的图形,判断即可。
【详解】据分析可知,扇形是由圆的两条半径和一段曲线围成的。原题说法正确。
故答案为:√
24.×
【分析】书的左右两页页码是相邻的自然数,相邻自然数一个是奇数一个是偶数,根据奇数和偶数的运算性质来判断它们乘积的奇偶性。
【详解】打开书,左右两页的页码必然是相邻的两个数,而相邻的两个自然数必定是一个奇数一个偶数。
根据奇数和偶数的运算性质,奇数×偶数=偶数。所以这两个相邻页码(一奇一偶)的乘积必然是偶数,而不是奇数。
所以原题说法错误。
故答案为:×
25.√
【分析】本题涉及最小公倍数和最大公因数的概念。最小公倍数是两个数公有的倍数中最小的那个数,最大公因数是两个数公有的因数中最大的那个数。我们可以通过举例或者从概念的性质来进行判断。
【详解】1. 考虑特殊情况
假设两个数是倍数关系,比如2和4 。
先求最大公因数, 2的因数有1 、2 ,4 的因数有1 、2 、 4,它们公有的因数中最大的是2 ,所以2 和 4的最大公因数是 2。
再求最小公倍数, 2的倍数有2 、4 ,4 的倍数有4 、8 ,它们公有的倍数中最小的是4 ,所以2 和 4的最小公倍数是 4。
此时最小公倍数大于最大公因数 。
2. 一般情况分析
对于任意两个不同的非0自然数,最大公因数是这两个数公有的因数的乘积,而最小公倍数不仅包含了公有的因数,还包含了各自独有的因数。所以从概念本质上来说,最小公倍数一定包含了最大公因数,并且还有其他因数,所以最小公倍数总是大于这两个数的最大公因数。原题干说法正确。
故答案为:√
26.x=0.8;x=3.5;x=
【分析】(1)根据等式的基本性质:方程两边同时加上0.44,然后两边再同时除以1.3即可;
(2)根据等式的基本性质:方程两边同时减去1.5;
(3)根据等式的基本性质:方程两边同时加上x,两边再同时减去 。
【详解】(1)1.3x-0.44=0.6
解:1.3x-0.44+0.44=0.6+0.44
1.3x=1.04
1.3x÷1.3=1.04÷1.3
x=0.8
(2)x- +2=5
解:x+ -1.5=5-1.5
x=3.5
(3) -x=
解:
27.1;;;;
;;0.56;0.36
【解析】略
28.78.5平方米
【分析】牛最多可吃到草的面积就是以木桩为圆心,绳长为半径的圆的面积。
【详解】
(平方米)
答:牛所能吃到草的最大面积是78.5平方米。
【点睛】本题主要考查圆的面积公式。能理解牛最多可吃到草的面积就是以木桩为圆心,绳长为半径的圆的面积是解题的关键。
29.(1)见详解
(2)2020年计划产量和实际产量相等(答案不唯一)
【分析】(1)由图可知,实线表示实际产量,虚线表示计划产量,2020、2021、2022、2023年的计划产量分别为8万个、10万个、13万个、16万个,实际产量分别为8万个、12万个、16万个、18万个;用算式8+10+13+16求得计划产量合计,用算式8+12+16+18求得实际产量合计。据此解答即可。
(2)从图表中,可以看到2020年计划产量和实际产量都是8万元,也就是计划产量和实际产量相等。(答案不唯一)
【详解】(1)8+10+13+16
=31+16
=47(万个)
8+12+16+18
=36+18
=54(万个)
所以:
某电子厂2020~2023年一种电子元件的产量统计表 2024年12月
年份 合计 2020 2021 2022 2023
计划产量/万个 47 8 10 13 16
实际产量/万个 54 8 12 16 18
(2)从图表中,我知道了2020年计划产量和实际产量相等。(答案不唯一)
30.17人;150本
【分析】由于买来的书的本数不变,设阅读组有x人;平均每人份8本,x人分8x本,还剩14本,用8x+14=买来书的本数;给每人分9本,最后一人只能分得6本;(x-1)人分9本书,1人分6本书,(x-1)人分9×(x-1)本,(x-1)人分的本数+1人分的6本书=买来书的本数,列方程:8x+14=9×(x-1)+6,解方程,求出阅读组的人数,进而求出买书的本数,据此解答。
【详解】解:设阅读组有x人。
8x+14=9×(x-1)+6
8x+14=9x-9+6
8x+14-8x+9-6=9x-9+6+9-6-8x
x=14+9-6
x=17
17×8+14
=136+14
=150(本)
答:阅读组有17人,李老师共买来150本书。
31.12位
【分析】由题意可知,图书和益智玩具如果分的没有剩余,则图书有46+2=48(套),益智玩具有37-1=36(个),要想每人分得的数量相等,最多有多少位同学获得一等奖,就是求48和36的最大公因数。据此解答。
【详解】46+2=48(套)
37-1=36(个)
48=2×2×2×2×3
36=2×2×3×3
48和36的最大公因数是:2×2×3=12
答:最多有12位同学获得一等奖。
【点睛】此题考查的是最大公因数的应用,求两个数的最大公因数的方法是把两个数共有的因数相乘。
32.12名
【分析】由于奶糖剩1颗,则奶糖分了:49-1=48(颗),48是第一小组人数的倍数;巧克力少一颗,如果巧克力再多一颗,就是这些学生的倍数,即35+1=36(棵),由此可知这组学生的人数是48和36的公因数,由于最多有多少名同学,则求48和36的最大公因数即可。
【详解】49-1=48(颗)
35+1=36(颗)
48=2×2×2×2×3
36=2×2×3×3
48和36的最大公因数:2×2×3=12
答:第一小组最多有12名同学。
【点睛】本题主要考查最大公因数的求法,熟练掌握最大公因数的求法是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末测试
一、选择题
1.车轮做成圆的,车轴应装在( )。
A.圆心位置 B.圆上任何位置 C.圆内任何位置 D.圆的直径上
2.如果是假分数,那么符合条件的x值有( )个。
A.3 B.4 C.5 D.无数
3.圆周率π是一个( )。
A.近似数 B.两位小数 C.无限不循环小数
4.甲绳比乙绳长米,丙绳比乙绳短米。甲绳与丙绳相比,( )。
A.甲绳长 B.甲绳短 C.一样长 D.无法确定哪根长
5.a、b是两个相邻自然数(a、b都不为0),a和b的最大公因数是( ),最小公倍数是( )。
A.1;ab B.ab;b C.a;ab D.b;b
6.把一个边长为12厘米的正方形铁丝改围成一个长方形,长方形的长是宽的3倍,设宽为厘米,则下列方程中,( )是正确的。
A. B.
C. D.
7.小军要用一张纸片,从中剪下一个面积是16π平方厘米的圆形纸片,应该选择下面的( )纸片。
A.边长是4厘米的正方形
B.长是8厘米,宽是6厘米的长方形
C.周长是28厘米的正方形
D.长是10厘米,宽是8厘米的长方形
8.105名同学参加团体操表演,如果要求每排人数必须相等,并且每排不能少于10人,不能多于30人,符合条件的队列一共有( )种。
A.1 B.2 C.3 D.4
9.算式“1×3×5×…×99×2”的积是( )。
A.质数 B.奇数 C.偶数 D.无法确定
10.一个圆形射击靶的周长是2.826米,射中靶心代表是10环,一个运动员射击时得了4环,他射中的位置距离靶心可能是( )厘米。
A.900 B.90 C.50 D.30
二、填空题
11.在①14-x=8;②7×5=35;③x÷0.9=1.8;④100a;⑤79<83x;⑥15y=6+x中,方程有( ),等式有( )。
12.分数加减混合运算的运算顺序和( )混合运算的运算顺序相同。
13.端午节期间,小明和爸爸去大洋湾观看龙舟赛。入住酒店后,小明问爸爸:“我们的房间号是多少?”爸爸说:“房间号由三个数字组成,第一个数字代表楼层,它既是质数又是偶数;后面两个数字代表房间顺序,它是20以内最大的奇数。”小明和爸爸的房间号是( )。
14.一根a米长的彩带,如果用去它的,还剩下它的 ;如果用去米,还剩下 米。
15.的分数单位是( ),它有( )个这样的分数单位。
16.五年级一班学生中,会打乒乓球的占,这里是把( )看作单位“1”,平均分成了( )份,会打乒乓球的学生占( )份。
17.把一根3米长的木料锯成相等的5小段,每段是这根木料的,是米。
18.在横线上填写最简分数。
18角= 元 18厘米 米 380千克= 吨
42分= 时 125平方分米= 平方米 32平方米= 公顷
19.先把数量关系补充完整,再列出方程。
(1)公交车上原有15人,到站后下车x人,又上车12人,车上现在18人。
数量关系:
方程:
(2)女儿今年x岁,妈妈今年年龄是女儿的3倍,比女儿大30岁。
数量关系:
方程:
20.数形结合是数学上常用的思想方法。观察图中小正方形的数量,其中灰白相间的小正方形的个数依次对应着奇数组成的算式中的每一个数。请你找出其中规律,用最简便的方法计算下面的算式。
(1)( )( )( )
(2)( )( )( )
三、判断题
21.一个圆的半径是3厘米,它的直径是6厘米。( )
22.把60分解质因数是60=2×3×10。( )
23.扇形是由圆的两条半径和一段曲线围成的。( )
24.打开数学书,左右两边页码的积是奇数。( )
25.两个不同的非0自然数的最小公倍数总是大于这两个数的最大公因数。( )
四、计算题
26.解方程。
1.3x-0.44=0.6 x-+2=5 -x=
27.直接写出得数。
五、解答题
28.在一块草地的木柱上拴着一头牛,拴牛的绳长为5米(拴在木桩上的绳子忽略不计),牛最多可吃到草的面积是多少平方米?
29.下面是某电子厂2020~2023年一种电子元件的产量统计图。
(1)请根据统计图完成下面的统计表。
____________统计表 _______年______月
年份 合计 2020 2021 2022 2023
计划产量/万个
实际产量/万个
(2)从图表中你还能获得哪些信息?
30.李老师买了一些故事书分给阅读小组的同学们,一开始平均每人分8本,还剩14本。李老师又重新调整分配方案,给每人分9本,最后一人只能分得6本,那么阅读组有多少人?李老师共买来多少本书?
31.大赛组委会把46本编程图书和37个益智玩具分别平均分给一等奖获得者,结果编程图书少2本,益智玩具剩1个,那么最多有多少位同学获得一等奖?
32.有49颗奶糖和35颗巧克力,平均分给第一小组的同学,结果奶糖剩一颗,巧克力少一颗。第一小组最多有多少名同学?
《期末测试》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A D C A A D D B C D
1.A
【分析】连接圆心和圆上任意一点的线段叫做半径。半径决定圆的大小,在同一个圆内有无数条半径,同一个圆内所有的半径都相等。
把车轴安装在车轮的圆心处,车开起来更平稳,是利用了同一个圆的半径都相等的特性。
【详解】车轮做成圆的,车轴应装在圆心位置。
故答案为:A
2.D
【分析】分子比分母大或者分子和分母相等的分数叫假分数,据此求解。
【详解】根据假分数的概念,只要,该数就是假分数,所以x的值有无数个。
故答案为:D
【点睛】本题主要考查假分数的概念。
3.C
【分析】圆周率π是圆的周长与直径的比值,在实际应用中,为了便于计算,我们常取π的近似值3.14 ,但实际上它的小数位无穷无尽且不存在循环节。
【详解】A.圆周率π是圆周长与直径的精确比值,并非近似数,只是计算时常用近似值,原题说法错误;
B.π=3.1415926…,小数位无限且无循环规律,不是两位小数,原题说法错误;
C.π小数点后数字无限且无循环节,符合无限不循环小数特征,原题说法正确。
故答案为:C
4.A
【分析】甲绳比乙绳长米,则甲绳的长度>乙绳的长度;丙绳比乙绳短米,则乙绳的长度>丙绳的长度,据此解答。
【详解】甲绳的长度>乙绳的长度,乙绳的长度>丙绳的长度,因此甲绳的长度>乙绳的长度>丙绳的长度,所以甲绳的长度>丙绳的长度,所以甲绳与丙绳相比,甲绳长。
故答案为:A
5.A
【分析】a、b是两个相邻自然数,如2和3,它们是互质数;根据“两个数是互质数时,它们的最大公因数是1,最小公倍数是两数的乘积”进行解答。
公因数只有1的两个非零自然数,叫做互质数。
【详解】a、b是两个相邻自然数(a、b都不为0),则a和b是互质数,a和b的最大公因数是(1),最小公倍数是(ab)。
故答案为:A
6.D
【分析】根据题意,找出数量关系:即正方形的周长等于长方形的周长;由正方形的周长=边长×4,长方形的周长=(长+宽)×2,代入相应数值即可列出方程。
【详解】解:设长方形的宽为厘米,则长方形的长为3x。
因此列出方程正确的是:。
故答案为:D
7.D
【分析】根据题意可知,要在一个长方形纸片上剪一个面积是16π平方厘米的圆,这个长方形的边长等于圆的直径(半径的2倍),首先根据圆的面积公式:S=πr2,已知圆的面积可以求出半径的平方,进而求出半径,然后进行选择即可。
【详解】解:设圆的半径为r厘米
πr2=16π
r2=16
因为4的平方是16,所以圆的半径是4厘米。
这张长方形纸片的长与宽不小于8厘米。
D的长与宽符合题意。
故答案为:D
【点睛】本题主要考查圆的面积公式的灵活运用,关键是熟记公式。
8.B
【分析】根据题意可知,每排人数×排数=总人数,要求每排人数必须相等,说明每排人数是105的因数;先列举出105的所有因数,再从中找出每排不少于10人,不多于30人的因数,即是符合条件的队列。
【详解】105的因数:1,3,5,7,15,21,35,105;
在10~30之间的因数是:15,21;
符合条件的队列是:
①每排15人,共7排;
②每排21人,共5排;
符合条件的队列一共有2种。
故答案为:B
9.C
【分析】奇数:不能被2整除的数是奇数;能被2整除的数是偶数;
质数:除了1和它本身,没有其它因数的数是质数;合数:除了1和它本身,还有其它因数的数是合数;
由于奇数×奇数=奇数,奇数×偶数=偶数,偶数×偶数=偶数,可知在乘法算式里,只有要偶数,那么结果一定是偶数,据此即可选择。
【详解】由分析可知:1×3×5×…×99×2里最后乘了2,2是偶数,所以它的积是偶数。
故答案为:C
10.D
【分析】根据圆的周长公式:C=2πr,计算其半径,再把半径平均分成10份,4环与靶心的距离应该在(10-4)份到(10-3)份之间。
【详解】2.826米=282.6厘米
282.6÷3.14÷2=45(厘米)
45÷10×(10-4)
=45÷10×6
=27(厘米)
45÷10×(10-3)
=45÷10×7
=31.5(厘米)
A.900>31.5,不符合题意;
B.90>31.5,不符合题意;
C.50>31.5,不符合题意;
D.27<30<31.5,符合题意;
他射中的位置距离靶心可能是30厘米。
故答案为:D
【点睛】本题关键是熟练掌握圆的周长公式,明确4环与靶心的距离范围。
11. ①③⑥ ①②③⑥
【分析】含有等号的式子叫等式;含有未知数的等式叫方程。据此判断。
【详解】14-x=8、x÷0.9=1.8、15y=6+x,即含有未知数又是等式,它们是方程。
14-x=8、x÷0.9=1.8、15y=6+x,7×5=35,含有等号,它们是等式。
方程有(①③⑥),等式有(①②③⑥)
【点睛】掌握等式、方程的概念是解答本题的关键。
12.整数
【详解】分数加减混合运算的运算顺序和(整数)混合运算的运算顺序相同。
如:
13.219
【分析】一个数,如果只有1和它本身两个因数,那么这样的数叫做质数;
一个数,如果除了1和它本身还有别的因数,那么这样的数叫做合数;
整数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数。
【详解】第一个数字代表楼层,它既是质数又是偶数,即2;
后面两个数字代表房间顺序,它是20以内最大的奇数,即19;
小明和爸爸的房间号是219。
【点睛】本题考查质数、偶数与奇数的意义及应用,明确2是最小的质数,也是偶数中唯一的质数。
14. a-
【分析】根据题意可知,把这根彩带看作单位“1”,由于用去它的,还剩下它的:1-,算出结果即可;由于用去米,即剩下的米数=总米数-用去的米数,由此即可求解。
【详解】1-=
用去米,还剩下:(a-)米。
【点睛】本题主要考查单位“1”的判断,要注意分数后面加单位表示具体的数。
15. 10
【分析】把单位“1”平均分成若干份取一份的数,叫做分数单位;分数的分子是几里面就有几个这样的分数单位。
【详解】由分析可得:
的分数单位是,的分子是10,所以有10个这样的分数单位。
16. 五年级一班总人数 9 5
【分析】根据分数的意义,由“五年级一班学生中,会打乒乓球的占”知:把五一班全部学生当作单位“1”,平均分成了9份,打乒乓球的点其中的5份。据此解答。
【详解】五年级一班学生中,会打乒乓球的占,这里是把(五年级一班总人数)看作单位“1”,平均分成了(9)份,会打乒乓球的学生占(5)份。
【点睛】此题主要考查了单位“1”的确定及分数的意义。
17.;
【分析】把这根木料的长度看作单位“1”,把它平均锯成5段,每段是总长度的;一根长3米的木料平均锯成5段,求每段长度,用这根木料的长度除以平均锯成的段数;据此解答。
【详解】1÷5=
3÷5=(米)
把一根3米长的木料锯成相等的5小段,每段是这根木料的,是米。
【点睛】解决此题关键是弄清求的是“分率”还是“具体的数量”,求分率:平均分的是单位“1”;求具体的数量:平均分的是具体的数量,要注意:分率不能带单位名称,而具体的数量要带单位名称。
18.
【分析】1元=10角;1米=100厘米;1吨=1000千克;1时=60分;1平方米=100平方分米;1公顷=10000平方米;低级单位换算成高级单位,除以进率;最简分数的意义:分子和分母只有公因数1,像这样的分数叫作最简分数,据此解答。
【详解】18角=元
18厘米=米
380千克=吨
42分=时
125平方分米=平方米
32平方米=时
【点睛】熟记进率以及最简分数的意义是解答本题的关键、
19.(1) 原来车上的人数-下车的人数+上车的人数=此时车上的人数 15-x+12=18
(2) 女儿年龄+30=女儿的年龄×3 x+30=3x
【分析】(1)由于下车的话,人数减少,上车人数增加,那么可知:原来车上的人数-下车的人数+上车的人数=此时车上的人数,据此即可列方程;
(2)由于妈妈今年年龄是女儿的3倍,那么女儿的年龄×3=妈妈的年龄,由于妈妈比女儿大30岁,那么女儿年龄+30=女儿的年龄×3,据此即可列方程。
【详解】(1)由分析可知:
数量关系:原来车上的人数-下车的人数+上车的人数=此时车上的人数
方程:15-x+12=18
(2)数量关系:女儿年龄+30=女儿的年龄×3
方程:x+30=3x
【点睛】本题主要考查列方程,找准等量关系是解题的关键。
20.(1) 100 10 10
(2) 2500 50 50
【分析】根据题干中给出的算式可以得到规律是:差是2,首项是1的等差数列的和等于项数乘项数。
【详解】(1)根据等差数列中项数=(末项+1)÷2可得:
(19+1)÷2
=20÷2
=10
因此。
(2)根据等差数列中项数=(末项+1)÷2可得:
(99+1)÷2
=100÷2
=50
因此。
【点睛】仔细观察给出的算式,找到规律是解决本题的关键。
21.√
【分析】在同一个圆或等圆中,直径是半径的2倍,半径是直径的一半,由此解答问题。
【详解】3×2=6(厘米)
一个圆的半径是3厘米,它的直径是6厘米。原说法正确。
故答案为:√
22.×
【分析】分解质因数是把合数分解成若干个质因数相乘的形式。
【详解】60=2×3×10中10不是质数,把60分解质因数应是60=2×2×3×5。
原题说法错误。
故答案为:×
23.√
【分析】根据扇形的意义:扇形是由圆的两条半径和一段曲线围成的图形,判断即可。
【详解】据分析可知,扇形是由圆的两条半径和一段曲线围成的。原题说法正确。
故答案为:√
24.×
【分析】书的左右两页页码是相邻的自然数,相邻自然数一个是奇数一个是偶数,根据奇数和偶数的运算性质来判断它们乘积的奇偶性。
【详解】打开书,左右两页的页码必然是相邻的两个数,而相邻的两个自然数必定是一个奇数一个偶数。
根据奇数和偶数的运算性质,奇数×偶数=偶数。所以这两个相邻页码(一奇一偶)的乘积必然是偶数,而不是奇数。
所以原题说法错误。
故答案为:×
25.√
【分析】本题涉及最小公倍数和最大公因数的概念。最小公倍数是两个数公有的倍数中最小的那个数,最大公因数是两个数公有的因数中最大的那个数。我们可以通过举例或者从概念的性质来进行判断。
【详解】1. 考虑特殊情况
假设两个数是倍数关系,比如2和4 。
先求最大公因数, 2的因数有1 、2 ,4 的因数有1 、2 、 4,它们公有的因数中最大的是2 ,所以2 和 4的最大公因数是 2。
再求最小公倍数, 2的倍数有2 、4 ,4 的倍数有4 、8 ,它们公有的倍数中最小的是4 ,所以2 和 4的最小公倍数是 4。
此时最小公倍数大于最大公因数 。
2. 一般情况分析
对于任意两个不同的非0自然数,最大公因数是这两个数公有的因数的乘积,而最小公倍数不仅包含了公有的因数,还包含了各自独有的因数。所以从概念本质上来说,最小公倍数一定包含了最大公因数,并且还有其他因数,所以最小公倍数总是大于这两个数的最大公因数。原题干说法正确。
故答案为:√
26.x=0.8;x=3.5;x=
【分析】(1)根据等式的基本性质:方程两边同时加上0.44,然后两边再同时除以1.3即可;
(2)根据等式的基本性质:方程两边同时减去1.5;
(3)根据等式的基本性质:方程两边同时加上x,两边再同时减去 。
【详解】(1)1.3x-0.44=0.6
解:1.3x-0.44+0.44=0.6+0.44
1.3x=1.04
1.3x÷1.3=1.04÷1.3
x=0.8
(2)x- +2=5
解:x+ -1.5=5-1.5
x=3.5
(3) -x=
解:
27.1;;;;
;;0.56;0.36
【解析】略
28.78.5平方米
【分析】牛最多可吃到草的面积就是以木桩为圆心,绳长为半径的圆的面积。
【详解】
(平方米)
答:牛所能吃到草的最大面积是78.5平方米。
【点睛】本题主要考查圆的面积公式。能理解牛最多可吃到草的面积就是以木桩为圆心,绳长为半径的圆的面积是解题的关键。
29.(1)见详解
(2)2020年计划产量和实际产量相等(答案不唯一)
【分析】(1)由图可知,实线表示实际产量,虚线表示计划产量,2020、2021、2022、2023年的计划产量分别为8万个、10万个、13万个、16万个,实际产量分别为8万个、12万个、16万个、18万个;用算式8+10+13+16求得计划产量合计,用算式8+12+16+18求得实际产量合计。据此解答即可。
(2)从图表中,可以看到2020年计划产量和实际产量都是8万元,也就是计划产量和实际产量相等。(答案不唯一)
【详解】(1)8+10+13+16
=31+16
=47(万个)
8+12+16+18
=36+18
=54(万个)
所以:
某电子厂2020~2023年一种电子元件的产量统计表 2024年12月
年份 合计 2020 2021 2022 2023
计划产量/万个 47 8 10 13 16
实际产量/万个 54 8 12 16 18
(2)从图表中,我知道了2020年计划产量和实际产量相等。(答案不唯一)
30.17人;150本
【分析】由于买来的书的本数不变,设阅读组有x人;平均每人份8本,x人分8x本,还剩14本,用8x+14=买来书的本数;给每人分9本,最后一人只能分得6本;(x-1)人分9本书,1人分6本书,(x-1)人分9×(x-1)本,(x-1)人分的本数+1人分的6本书=买来书的本数,列方程:8x+14=9×(x-1)+6,解方程,求出阅读组的人数,进而求出买书的本数,据此解答。
【详解】解:设阅读组有x人。
8x+14=9×(x-1)+6
8x+14=9x-9+6
8x+14-8x+9-6=9x-9+6+9-6-8x
x=14+9-6
x=17
17×8+14
=136+14
=150(本)
答:阅读组有17人,李老师共买来150本书。
31.12位
【分析】由题意可知,图书和益智玩具如果分的没有剩余,则图书有46+2=48(套),益智玩具有37-1=36(个),要想每人分得的数量相等,最多有多少位同学获得一等奖,就是求48和36的最大公因数。据此解答。
【详解】46+2=48(套)
37-1=36(个)
48=2×2×2×2×3
36=2×2×3×3
48和36的最大公因数是:2×2×3=12
答:最多有12位同学获得一等奖。
【点睛】此题考查的是最大公因数的应用,求两个数的最大公因数的方法是把两个数共有的因数相乘。
32.12名
【分析】由于奶糖剩1颗,则奶糖分了:49-1=48(颗),48是第一小组人数的倍数;巧克力少一颗,如果巧克力再多一颗,就是这些学生的倍数,即35+1=36(棵),由此可知这组学生的人数是48和36的公因数,由于最多有多少名同学,则求48和36的最大公因数即可。
【详解】49-1=48(颗)
35+1=36(颗)
48=2×2×2×2×3
36=2×2×3×3
48和36的最大公因数:2×2×3=12
答:第一小组最多有12名同学。
【点睛】本题主要考查最大公因数的求法,熟练掌握最大公因数的求法是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
