天津学大教育信息咨询有限公司(人教版)高一物理必修一教案:2-5 自由落体运动与竖直上抛运动
文档属性
| 名称 | 天津学大教育信息咨询有限公司(人教版)高一物理必修一教案:2-5 自由落体运动与竖直上抛运动 |  | |
| 格式 | zip | ||
| 文件大小 | 55.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2016-06-24 18:00:49 | ||
图片预览

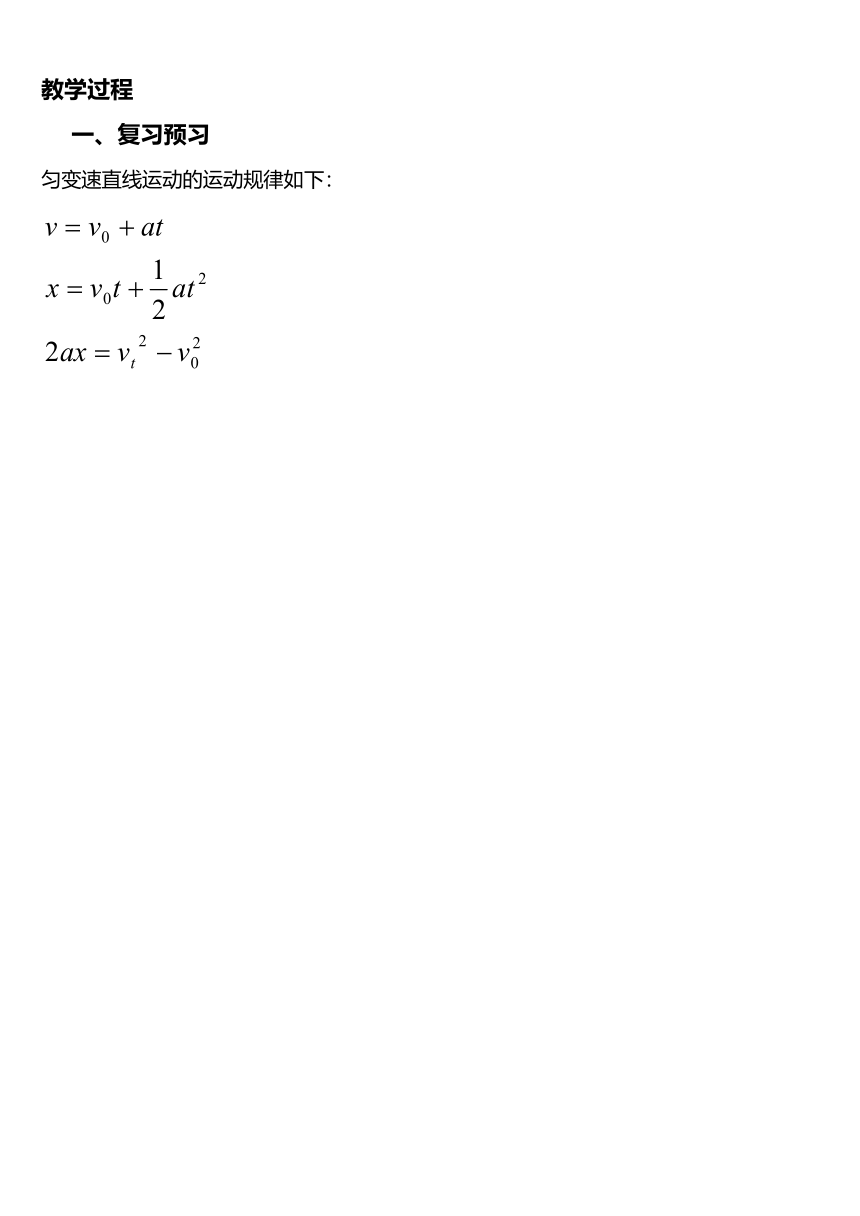



文档简介
自由落体运动与竖直上抛运动
适用学科
高中物理
适用年级
高中二年级
适用区域
人教版
课时时长(分钟)
60分钟(一对一)
知识点
1.
自由落体运动基本公式2.
竖直上抛运动特点3.
自由落体运动特点4.
竖直上抛运动基本公式5.
竖直上抛运动的导出公式和推论6.
自由落体运动的导出公式和推论
教学目标
1.知道自由落体运动和竖直上抛运动特点.2.能用公式和图象描述自由落体运动和竖直上抛运动.3.掌握竖直上抛运动的基本规律和两种常见处理方法.4.了解什么是竖直上抛运动.5.掌握竖直上抛运动的特征.6.掌握竖直上抛运动的规律.7.能熟练计算竖直上抛物体的位移、速度及运动时间。
教学重点
1.自由落体的运动规律及其应用.2.竖直上抛运动的规律及其应用.
教学难点
自由落体的运动规律及其应用.能用公式和图象描述自由落体运动和竖直上抛运动.掌握竖直上抛运动的基本规律和两种常见处理方法.
教学过程
一、复习预习
匀变速直线运动的运动规律如下:
二、知识讲解
考点/易错点1
自由落体运动
1.定义
物体只在重力作用下,从静止开始下落的运动。
2.运动性质
初速度为0,加速度为重力加速度的匀加速直线运动。
3.基本规律
(1)速度公式:v=gt
(2)位移公式:h=gt2
(3)速度位移关系式:v2=2gh
考点/易错点2
自由落体运动规律
1)速度公式
2)下落高度
3)下落时间
4)落地速度
考点/易错点3
竖直上抛运动
1.运动特点
加速度为g,上升阶段做匀减速直线运动,下落阶段做匀加速直线运动。[
2.运动规律
(1)速度公式:v=v0-gt
(2)位移公式:h=v0t-gt2
(3)速度—位移关系式:v2-v=-2gh
(4)上升的最大高度:H=
(5)上升到最大高度用时:t=
考点/易错点4
竖直上抛运动的导出公式和推论
(1)上升到最高点的时间t=v0/g
(推导:最高点v=0
由v=v0
-gt
可知:0=v0-gt,所以,到达最高点时间t
=v0/g)
(2)上升到最高点所用时间与落回到抛出点所用时间相等。
(3)上升的最大高度H=v02/2g
(推导:因为最高点
v
=0,由vt2-v02=-2gH得H=v02/2g)
考点/易错点5
1.竖直上抛运动的研究方法
竖直上抛运动的实质是加速度恒为g的匀变速运动,处理时可采用两种方法:
(1)分段法:将全程分为两个阶段,即上升过程的匀减速阶段和下落过程的自由落体阶段。
(2)全程法:将全过程视为初速度为v0,加速度a=-g的匀变速直线运动,必须注意物理量的矢量性。习惯上取v0的方向为正方向,则
①v>0时,物体正在上升;v<0时,物体正在下降;
②h>0时,物体在抛出点上方;h<0时,物体在抛出点下方。
2.竖直上抛运动的对称性
如图所示,物体以初速度v0竖直上抛,A、B为途中的任意两点,C为最高点,则:
( http: / / www.21cnjy.com )
(1)时间对称性:物体上升过程中从A→C所用时间tAC和下降过程中从C→A所用时间tCA相等,同理有tAB=tBA
(2)速度对称性:物体上升过程经过A点的速度与下降过程经过A点的速度大小相等。
(3)能量对称性:物体从A→B和从B→A重力势能变化量的大小相等,均等于mghAB
三、例题精析
【例题1】
【题干】在学习了伽利略对自由落体运动的研究后,甲同学给乙同学出了这样一道题:一个物体从塔顶落下(不考虑空气阻力),物体到达地面前最后一秒内通过的位移为整个位移的9/25,求塔高H(取g=10
m/s2)。
乙同学的解法:根据h=gt2得物体在最后1
s内的位移h1=gt2=5
m,再根据=得H=13.9
m,乙同学的解法是否正确?如果正确说明理由,如果不正确请给出正确解析过程和答案。
【答案】125m
【解析】乙同学的解法不正确。根据题意画出
( http: / / www.21cnjy.com )运动过程示意图,设物体从塔顶落到地面所经历的时间为t,通过的位移为H,物体在(t-1)秒内的位移为h。
据自由落体运动规律,有H=gt2
h=g(t-1)2
由题意得==
联立以上各式解得H=125
m
( http: / / www.21cnjy.com )
【例题2】
【题干】一个氢气球以4
m/s2的加速
( http: / / www.21cnjy.com )度由静止从地面竖直上升,10
s末从气球上掉下一重物,此重物最高可上升到距地面多高处?此重物从氢气球上掉下后,经多长时间落回到地面(忽略空气阻力,g取10
m/s2)
【答案】280
m 11.48
s
【解析】下面分三个阶段来求解
向上加速阶段:a1=4
m/s2t1=10
s,H1=a1t=×4×102
m=200
m
v1=a1t1=4×10
m/s=40
m/s。
竖直上抛阶段:a2=-10
m/s2,v0=v1=40
m/s
上升的高度:H2==
m=80
m
所用时间:t2==
s=4
s
所以重物距地面的最大高度为:
Hmax=H1+H2=200
m+80
m=280
m。
自由下落阶段:加速度a3=10
m/s2,
下落的高度H3=280
m。
下落所用的时间:
t3=
=
s=
s≈7.48
s
所以重物从氢气球上掉下后,落回地面所用的时间为:
t=t2+t3=4
s+7.48
s=11.48
s。
【例题3】
【题干】(2004
广东)一杂技演员,用一只手抛球、接球.他每隔0.40s抛出一球,接到球便立即把球抛出.已知除正在抛、接球的时刻外,空中总有4个球.将球的运动近似看做是竖直方向的运动,球到达的最大高度是(高度从抛球点算起,取):
A.1.6m
B.2.4m
C.3.2m
D.4.0m
【答案】C
【解析】空中总有四个球,每两个相邻的球间的时间间隔为0.40s,则每个球上往返时间为1.60s,即上升阶段时间为0.80s,根据竖直上抛运动规律可知,上升和下落时间对称,故球达到的最大高度为:.
四、课堂运用
【基础】
1、将一个物体以某一速度从地面竖直向上抛出,设物体在运动过程中所受空气阻力大小不变,则物体( )
A.刚抛出时的速度最大
B.在最高点的加速度为零
C.上升时间大于下落时间
D.上升时的加速度等于下落时的加速度
【答案】A
【解析】A、整个过程中只有空气的阻力做功不为零,机械能损失,故上升过程初速度最大,故A正确;
BD、物体在运动过程中所受空气阻力大小不变,但是受空气阻力的方向总与物体的速度方向相反,,所以上升时的加速度大于下落时的加速度,B错误,D也错误;
C、根据上升时间小于下落时间,C错误;
故选A.
2、关于竖直上抛运动,下列说法正确的是( )
A.在最高点速度为零,加速度也为零
B.上升的时间小于下落过程的时间
C.从上升到下降的整个过程中加速度保持不变
D.上升到某一高度时速度小于下降到此高度时的速度
【答案】C
【解析】A、最高点速度为零,但是仍受重力,
( http: / / www.21cnjy.com )故加速仍为重力加速度,故A错误
B、上抛的运动时具有对称性的,上下的时间相等,故B错误
C、上升和下降的过程加速都是重力加速度,故C正确
D、由于竖直上抛机械能守恒,故可以知任何位置有固定的速度,不会因处于上升还是下降过程而改变此点的速度,故D错误
【巩固】
1、竖直上抛一物体,上升的最大高度为5m,求:抛出时的初速度大小
【答案】10m/s
【解析】因为从上抛最大高度自由下落的末速度与抛出时初速度大小相等,所以初速
2、从地面以相同的初速度先后竖直向上抛出两个小球,不计空气阻力,则在小球落地前( )
A.某一时刻两小球的位移可能相等
B.某一时刻两小球的速度可能相等
C.任意时刻两小球的位移差都相等
D.任意时刻两小球的速度差都相等
【答案】AD
【解析】设两个小球的时间差为△t,
A、由小球的位移:h=v0t gt2,h′=v0(t △t) g(t △t)2.所以当前一个小球下落的阶段,后一个小球仍然上升时,两个小球可能相遇.故A正确;
B、由速度时间公式得:v1=v0-gt,v2=v0-g(t-△t).由于存在时间差,所以两个小球的速度不可能相同.故B错误;
C、由小球的位移:h=v0t gt2,h′=v0(t △t) g(t △t)2.两个小球的位移差:△h=h h′=v0△t+gt△t g△t2,与时间t为一次函数关系.故C错误;
D、由速度时间公式得:v1=v0-gt,v2=v0-g(t-△t).
两个小球的速度差:△v=v1-v2=g△t是一个常数.故D正确.
【拔高】
1、某物体以30
m/s的初速度竖直上抛,不计空气阻力,g取10
m/s2,5
s内物体的( )
A.路程为65
m
B.位移大小为25
m,方向向上
C.速度改变量的大小为10
m/s
D.平均速度大小为13
m/s,方向向上
【答案】AB
【解析】上升到最高点所用时间为:t==3
s上升的路程为h1=gt2=×10×32
m=45
m,下降的位移为:h2=g(5-t)2=×10×22
m=20
m,故5
s内的路程为:s=h1+h2=65
m,A对;位移大小为:x=h1-h2=25
m,方向向上,B对;速度改变量大小为:Δv=gΔt=10×5
m/s=50
m/s,C错;平均速度大小为:==5
m/s,方向向上,D错。
2、在高为h处,小球A由静
( http: / / www.21cnjy.com )止开始自由落下,与此同时,在A的正下方地面上以初速度v0竖直向上抛出另一小球B,求A、B在空中相遇的时间与地点,并讨论A、B相遇的条件(不计空气阻力作用,重力加速度为g)。
【答案】当在B球的最高点相遇时,应有gt2+=h,且t=,解得v0=。
当
时,在B球上升过程中两球相遇。
【解析】设相遇时间为t,相遇点离地面高度为y,则两球相遇必在同一位置,具有相同的y。所以
y=v0t-gt2=h-gt2,
即v0t=h。所以相遇时间为t=。
将t代入y的表达式中,y=h-gt2=h-g=h(1-),即为相遇点离地面的高度。
讨论:若A、B能在空中相遇,则y>0,即h(1-)>0。
所以1->0,即v0>为A、B在空中相遇的条件。
当在B球的最高点相遇时,应有gt2+=h,且t=,解得v0=。
当
时,在B球上升过程中两球相遇。
五、课程小结
自由落体
;
;
竖直上抛
抛出时刻为t=0时刻.
物体上升最高点所用时间:
;
上升的最大高度:
物体下落时间(从抛出点——回到抛出点):
适用学科
高中物理
适用年级
高中二年级
适用区域
人教版
课时时长(分钟)
60分钟(一对一)
知识点
1.
自由落体运动基本公式2.
竖直上抛运动特点3.
自由落体运动特点4.
竖直上抛运动基本公式5.
竖直上抛运动的导出公式和推论6.
自由落体运动的导出公式和推论
教学目标
1.知道自由落体运动和竖直上抛运动特点.2.能用公式和图象描述自由落体运动和竖直上抛运动.3.掌握竖直上抛运动的基本规律和两种常见处理方法.4.了解什么是竖直上抛运动.5.掌握竖直上抛运动的特征.6.掌握竖直上抛运动的规律.7.能熟练计算竖直上抛物体的位移、速度及运动时间。
教学重点
1.自由落体的运动规律及其应用.2.竖直上抛运动的规律及其应用.
教学难点
自由落体的运动规律及其应用.能用公式和图象描述自由落体运动和竖直上抛运动.掌握竖直上抛运动的基本规律和两种常见处理方法.
教学过程
一、复习预习
匀变速直线运动的运动规律如下:
二、知识讲解
考点/易错点1
自由落体运动
1.定义
物体只在重力作用下,从静止开始下落的运动。
2.运动性质
初速度为0,加速度为重力加速度的匀加速直线运动。
3.基本规律
(1)速度公式:v=gt
(2)位移公式:h=gt2
(3)速度位移关系式:v2=2gh
考点/易错点2
自由落体运动规律
1)速度公式
2)下落高度
3)下落时间
4)落地速度
考点/易错点3
竖直上抛运动
1.运动特点
加速度为g,上升阶段做匀减速直线运动,下落阶段做匀加速直线运动。[
2.运动规律
(1)速度公式:v=v0-gt
(2)位移公式:h=v0t-gt2
(3)速度—位移关系式:v2-v=-2gh
(4)上升的最大高度:H=
(5)上升到最大高度用时:t=
考点/易错点4
竖直上抛运动的导出公式和推论
(1)上升到最高点的时间t=v0/g
(推导:最高点v=0
由v=v0
-gt
可知:0=v0-gt,所以,到达最高点时间t
=v0/g)
(2)上升到最高点所用时间与落回到抛出点所用时间相等。
(3)上升的最大高度H=v02/2g
(推导:因为最高点
v
=0,由vt2-v02=-2gH得H=v02/2g)
考点/易错点5
1.竖直上抛运动的研究方法
竖直上抛运动的实质是加速度恒为g的匀变速运动,处理时可采用两种方法:
(1)分段法:将全程分为两个阶段,即上升过程的匀减速阶段和下落过程的自由落体阶段。
(2)全程法:将全过程视为初速度为v0,加速度a=-g的匀变速直线运动,必须注意物理量的矢量性。习惯上取v0的方向为正方向,则
①v>0时,物体正在上升;v<0时,物体正在下降;
②h>0时,物体在抛出点上方;h<0时,物体在抛出点下方。
2.竖直上抛运动的对称性
如图所示,物体以初速度v0竖直上抛,A、B为途中的任意两点,C为最高点,则:
( http: / / www.21cnjy.com )
(1)时间对称性:物体上升过程中从A→C所用时间tAC和下降过程中从C→A所用时间tCA相等,同理有tAB=tBA
(2)速度对称性:物体上升过程经过A点的速度与下降过程经过A点的速度大小相等。
(3)能量对称性:物体从A→B和从B→A重力势能变化量的大小相等,均等于mghAB
三、例题精析
【例题1】
【题干】在学习了伽利略对自由落体运动的研究后,甲同学给乙同学出了这样一道题:一个物体从塔顶落下(不考虑空气阻力),物体到达地面前最后一秒内通过的位移为整个位移的9/25,求塔高H(取g=10
m/s2)。
乙同学的解法:根据h=gt2得物体在最后1
s内的位移h1=gt2=5
m,再根据=得H=13.9
m,乙同学的解法是否正确?如果正确说明理由,如果不正确请给出正确解析过程和答案。
【答案】125m
【解析】乙同学的解法不正确。根据题意画出
( http: / / www.21cnjy.com )运动过程示意图,设物体从塔顶落到地面所经历的时间为t,通过的位移为H,物体在(t-1)秒内的位移为h。
据自由落体运动规律,有H=gt2
h=g(t-1)2
由题意得==
联立以上各式解得H=125
m
( http: / / www.21cnjy.com )
【例题2】
【题干】一个氢气球以4
m/s2的加速
( http: / / www.21cnjy.com )度由静止从地面竖直上升,10
s末从气球上掉下一重物,此重物最高可上升到距地面多高处?此重物从氢气球上掉下后,经多长时间落回到地面(忽略空气阻力,g取10
m/s2)
【答案】280
m 11.48
s
【解析】下面分三个阶段来求解
向上加速阶段:a1=4
m/s2t1=10
s,H1=a1t=×4×102
m=200
m
v1=a1t1=4×10
m/s=40
m/s。
竖直上抛阶段:a2=-10
m/s2,v0=v1=40
m/s
上升的高度:H2==
m=80
m
所用时间:t2==
s=4
s
所以重物距地面的最大高度为:
Hmax=H1+H2=200
m+80
m=280
m。
自由下落阶段:加速度a3=10
m/s2,
下落的高度H3=280
m。
下落所用的时间:
t3=
=
s=
s≈7.48
s
所以重物从氢气球上掉下后,落回地面所用的时间为:
t=t2+t3=4
s+7.48
s=11.48
s。
【例题3】
【题干】(2004
广东)一杂技演员,用一只手抛球、接球.他每隔0.40s抛出一球,接到球便立即把球抛出.已知除正在抛、接球的时刻外,空中总有4个球.将球的运动近似看做是竖直方向的运动,球到达的最大高度是(高度从抛球点算起,取):
A.1.6m
B.2.4m
C.3.2m
D.4.0m
【答案】C
【解析】空中总有四个球,每两个相邻的球间的时间间隔为0.40s,则每个球上往返时间为1.60s,即上升阶段时间为0.80s,根据竖直上抛运动规律可知,上升和下落时间对称,故球达到的最大高度为:.
四、课堂运用
【基础】
1、将一个物体以某一速度从地面竖直向上抛出,设物体在运动过程中所受空气阻力大小不变,则物体( )
A.刚抛出时的速度最大
B.在最高点的加速度为零
C.上升时间大于下落时间
D.上升时的加速度等于下落时的加速度
【答案】A
【解析】A、整个过程中只有空气的阻力做功不为零,机械能损失,故上升过程初速度最大,故A正确;
BD、物体在运动过程中所受空气阻力大小不变,但是受空气阻力的方向总与物体的速度方向相反,,所以上升时的加速度大于下落时的加速度,B错误,D也错误;
C、根据上升时间小于下落时间,C错误;
故选A.
2、关于竖直上抛运动,下列说法正确的是( )
A.在最高点速度为零,加速度也为零
B.上升的时间小于下落过程的时间
C.从上升到下降的整个过程中加速度保持不变
D.上升到某一高度时速度小于下降到此高度时的速度
【答案】C
【解析】A、最高点速度为零,但是仍受重力,
( http: / / www.21cnjy.com )故加速仍为重力加速度,故A错误
B、上抛的运动时具有对称性的,上下的时间相等,故B错误
C、上升和下降的过程加速都是重力加速度,故C正确
D、由于竖直上抛机械能守恒,故可以知任何位置有固定的速度,不会因处于上升还是下降过程而改变此点的速度,故D错误
【巩固】
1、竖直上抛一物体,上升的最大高度为5m,求:抛出时的初速度大小
【答案】10m/s
【解析】因为从上抛最大高度自由下落的末速度与抛出时初速度大小相等,所以初速
2、从地面以相同的初速度先后竖直向上抛出两个小球,不计空气阻力,则在小球落地前( )
A.某一时刻两小球的位移可能相等
B.某一时刻两小球的速度可能相等
C.任意时刻两小球的位移差都相等
D.任意时刻两小球的速度差都相等
【答案】AD
【解析】设两个小球的时间差为△t,
A、由小球的位移:h=v0t gt2,h′=v0(t △t) g(t △t)2.所以当前一个小球下落的阶段,后一个小球仍然上升时,两个小球可能相遇.故A正确;
B、由速度时间公式得:v1=v0-gt,v2=v0-g(t-△t).由于存在时间差,所以两个小球的速度不可能相同.故B错误;
C、由小球的位移:h=v0t gt2,h′=v0(t △t) g(t △t)2.两个小球的位移差:△h=h h′=v0△t+gt△t g△t2,与时间t为一次函数关系.故C错误;
D、由速度时间公式得:v1=v0-gt,v2=v0-g(t-△t).
两个小球的速度差:△v=v1-v2=g△t是一个常数.故D正确.
【拔高】
1、某物体以30
m/s的初速度竖直上抛,不计空气阻力,g取10
m/s2,5
s内物体的( )
A.路程为65
m
B.位移大小为25
m,方向向上
C.速度改变量的大小为10
m/s
D.平均速度大小为13
m/s,方向向上
【答案】AB
【解析】上升到最高点所用时间为:t==3
s上升的路程为h1=gt2=×10×32
m=45
m,下降的位移为:h2=g(5-t)2=×10×22
m=20
m,故5
s内的路程为:s=h1+h2=65
m,A对;位移大小为:x=h1-h2=25
m,方向向上,B对;速度改变量大小为:Δv=gΔt=10×5
m/s=50
m/s,C错;平均速度大小为:==5
m/s,方向向上,D错。
2、在高为h处,小球A由静
( http: / / www.21cnjy.com )止开始自由落下,与此同时,在A的正下方地面上以初速度v0竖直向上抛出另一小球B,求A、B在空中相遇的时间与地点,并讨论A、B相遇的条件(不计空气阻力作用,重力加速度为g)。
【答案】当在B球的最高点相遇时,应有gt2+=h,且t=,解得v0=。
当
【解析】设相遇时间为t,相遇点离地面高度为y,则两球相遇必在同一位置,具有相同的y。所以
y=v0t-gt2=h-gt2,
即v0t=h。所以相遇时间为t=。
将t代入y的表达式中,y=h-gt2=h-g=h(1-),即为相遇点离地面的高度。
讨论:若A、B能在空中相遇,则y>0,即h(1-)>0。
所以1->0,即v0>为A、B在空中相遇的条件。
当在B球的最高点相遇时,应有gt2+=h,且t=,解得v0=。
当
五、课程小结
自由落体
;
;
竖直上抛
抛出时刻为t=0时刻.
物体上升最高点所用时间:
;
上升的最大高度:
物体下落时间(从抛出点——回到抛出点):
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
