第13章 三角形中的边角关系、命题与证明 小结与复习课件(共26张PPT)
文档属性
| 名称 | 第13章 三角形中的边角关系、命题与证明 小结与复习课件(共26张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 539.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-07 18:19:16 | ||
图片预览







文档简介
(共26张PPT)
①三角形有三条边,三个内角,三个顶点;
②组成三角形的线段叫做三角形的边;
③相邻两边所组成的角叫做三角形内角,简称角;
④相邻两边的公共端点是三角形的顶点;
⑤三角形 ABC 用符号表示为△ABC;
⑥三角形 ABC 的边 AB 可用边 AB 所对的角 C 的小写字母 c 表示,AC 可用 b 表示,BC 可用 a 表示.
A
B
C
不在同一直线上的三条线段首尾依次相接组成的图形叫做三角形.
一、三角形的相关概念
注意:
1.三边关系的依据是:两点之间线段最短.
2.判断三条线段能否构成三角形的方法:只要满足较小的两条线段之和大于第三条线段,便可构成三角形;若不满足,则不能构成三角形.
3.三角形第三边的取值范围是:
两边之差<第三边<两边之和
三角形的任意两边之和大于第三边;
三角形的任意两边之差小于第三边.
二、三角形的三边关系
1. 三角形的高:从三角形的一个顶点向它的对边所在 的直线作垂线,顶点和垂足之间的线段.
表示法:① AD 是△ABC 的边 BC 上的高;
② AD⊥BC 于 D;③∠ADB =∠ADC = 90°.
三、三角形的高、中线、角平分线:
注意:① 三角形的高是线段;
② 锐角三角形三条高全在三角形的内部;
直角三角形有两条高是直角边,另一条在内部;
钝角三角形有两条高在三角形外,另一条在内部.
③ 三角形三条高所在直线交于一点.
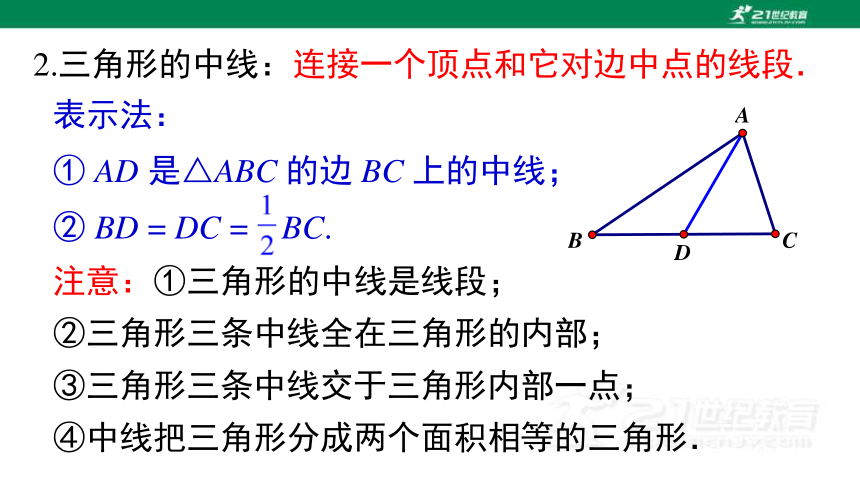
注意:①三角形的中线是线段;
②三角形三条中线全在三角形的内部;
③三角形三条中线交于三角形内部一点;
④中线把三角形分成两个面积相等的三角形.
2.三角形的中线:连接一个顶点和它对边中点的线段.
表示法:
① AD 是△ABC 的边 BC 上的中线;
② BD = DC = BC.
注意:①三角形的角平分线是线段;
②三角形三条角平分线全在三角形的内部;
③三角形三条角平分线交于三角形内部一点;
④用量角器画三角形的角平分线.
3. 三角形的角平分线:三角形一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段.
表示法:
① AD 是△ABC 中∠BAC 的平分线.
② ∠1 =∠2 = ∠BAC.
1
2
(
(
注意:① 命题有真命题和假命题两种.
对某一事件作出正确或不正确判断的语句叫做命题.
② 命题由题设和结论两部分组成. 前一部分称之为条件,后一部分称之为结论.
③ 命题通常是用“如果······ 那么······”的形式给出.
④ “如果 p,那么 q”中的题设与结论互换,得一个新命题:“如果 q,那么 p” 这两个命题称为互逆命题.其中一个命题叫做原命题,另一个命题叫做逆命题.
四、命题与证明
⑤ 当一个命题是真命题时它的逆命题不一定是真命题.
⑥ 符合命题的题设,但不满足命题的结论的例子,称之为反例. 要说明一个命题是假命题,只要举一个反例即可.
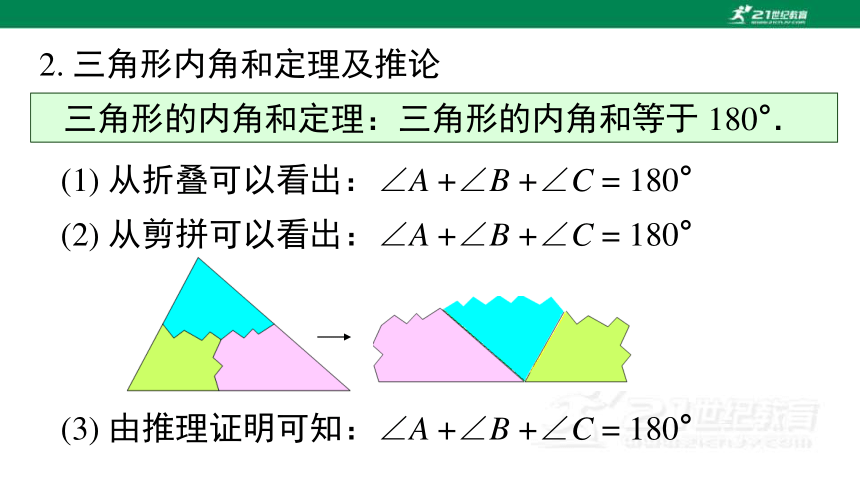
三角形的内角和定理:三角形的内角和等于 180°.
(2) 从剪拼可以看出:∠A +∠B +∠C = 180°
(1) 从折叠可以看出:∠A +∠B +∠C = 180°
(3) 由推理证明可知:∠A +∠B +∠C = 180°
2. 三角形内角和定理及推论
三角形的外角的定义:由三角形一边与另一边的延长线组成的角,叫做三角形的外角.
三角形的外角与内角的关系:
2.三角形的一个外角等于与它不相邻的两个内角的和;
1.三角形的一个外角与它相邻的内角互补;
3.三角形的一个外角大于任何一个与它不相邻的内角;
4.三角形的外角和为 360°.
考点一 三角形的三边关系
例1 已知两条线段的长分别是 3 cm、8 cm ,要想拼成一个三角形,且第三条线段 a 的长为奇数,问第三条线段应取多长?
解:由三角形两边之和大于第三边,两边之差小于
第三边,得 8 - 3<a<8 + 3,
∴ 5<a<11.
又∵第三边长为奇数,
∴ 第三条边长为 7 cm 或 9 cm.
三角形两边之和大于第三边,可以用来判断三条线段能否组成三角形,在运用中一定要注意检查是否任意两边的和都大于第三边,也可以直接检查较小两边之和是否大于第三边.三角形的三边关系在求线段的取值范围以及在证明线段的不等关系中有着重要的作用.
方法总结
2.在等腰三角形 ABC 中,它的两边长分别为 8 cm 和3 cm,则它的周长为________cm.
1.已知四组线段的长分别如下,以各组线段为边,能组成三角形的是( )
A.1,2,3 B.2,5,8
C.3,4,5 D.4,5,10
C
针对训练
19
3.以线段 3、4、x - 5 为边组成三角形,那么 x 的取值范围是 .
6<x<12
考点二 三角形内角和定理及推论
例2 下列条件中,能判定△ABC 为直角三角形的是 ( )
A.∠A = 2∠B = 3∠C B.∠A +∠B = 2∠C
C.∠A =∠B = 30° D.∠A = ∠B = ∠C
【分析】根据“三角形内角和定理和为180°”求出各选项中△ABC 的内角,然后根据直角三角形的判定方法进行判断.【答案】故选 D.
D
三角形内角和定理:三角形内角和是 180°.其推论为直角三角形两锐角互补及有两个角的和为 90° 的三角形是直角三角形.已知三角形中的三角形之间关系,可运用方程思想来求各角的度数.
方法总结
针对训练
4. 在一个直角三角形中,有一个锐角等于 60°,则另一个锐角的度数为_____.
30°
△ABC 中,∠B = ∠A = ∠C,求△ABC 的三个内角度数.
解:设∠B = x° ,则∠A = 3x°,∠C = 4x°,
从而 x + 3x + 4x = 180°,
解得 x = 22.5°.
即∠B = 22.5°,∠A = 67.5°,∠C = 90°.
考点三 三角形的角平分线、中线和高
例3 下列说法错误的是( )
A.三角形的三条中线都在三角形内,且平分三角形面积
B.直角三角形的高线只有一条
C.三角形的三条角平分线都在三角形内
D.钝角三角形内只有一条高线
B
【分析】根据三角形的角平分线、中线和高的概念逐一进行判断.【答案】B
三角形的三条角平分线、三条中线、三条高 (或延长线) 分别相交于一点,其中中线平分三角形面积,直角三角形有两条高线在直角边上,钝角三角形有两条高在三角形的外面.
方法总结
针对训练
6. 如图所示,AD 是△ABC 的中线,已知△ABD 比△ACD 的周长大 6 cm,则 AB 与 AC 的差为( )
A. 12 cm B. 6 cm
C. 3 cm D. 2 cm
B
A
B
C
D
7. 如图,在△ABC 中,∠ABC ,∠ACB 的平分线 BD,
CE 交于点 O.
(1) 若∠A = 80°,则∠BOC = .
(2) 你能猜想出∠BOC 与∠A 之间的数量关系吗?
130°
∠BOC = 90° + ∠A
A
B
C
O
E
D
例4 分别写出下列命题的条件及结论,并判断真假,是假命题的举出反例.
(1)如果两个角相等,那么它们是对顶角;
(2)如果 a>b,b>c,那么 a>c;
(3)三角形的中线平分该三角形的面积.
考点四 命题与证明
【分析】先把各个命题写成“如果……那么……”的形式,方便找出条件及结论.
解:(1) 条件:两个角相等,结论:它们是对顶角.
假命题,反例:两个角也有可能是两条平行线的同位角或内错角.
(2) 条件: a>b,b>c,结论: a>c,真命题.
(3) 条件:三角形的一条中线分三角形为两个小三角形,结论:这两个小三角形面积相等. 真命题.
方法总结
说明假命题的方法:
举反例
使之具有命题的条件,而不具有命题的结论.
∵直线 AB 与直线 CD 相交于点 O (已知),
8. 如图,直线 AB 与直线 CD 相交于点 O,∠AOC 与∠BOD 是对顶角. 求证:∠AOC =∠BOD.
证明:
∴ ∠AOB 与∠COD 都是平角(平角的定义).
∴ ∠AOC+∠AOD=180°,
∴ ∠AOC =∠BOD(同角的补角相等) .
∠BOD+∠AOD=180°(补角的定义) .
针对训练
例5 如图,求证:∠A +∠B +∠C =∠ADC.
考点五 三角形的外角
【分析】作射线 BD.通过三角形外角的性质进行转化即可求证.
证明:如图,作射线 BD.
A
B
C
D
E
)
)
)
)
1
2
3
4
根据三角形外角的性质,
则有∠3 =∠1 +∠A ①,∠4 =∠2 +∠C ②.
由① + ②得∠3 +∠4 =∠1 +∠A +∠2 +∠C,
故∠A+∠B+∠C =∠ADC 得证.
这是一个常见的几何图形模型,因为它像飞镖,故称之为“飞镖模型”.它利用三角形外角的性质推出四角之间的数量关系,即∠A +∠B +∠C =∠ADC.运用这一结论,能提高我们解题的准确性和速度.
方法总结
其他证法:如图
A
B
C
D
A
B
C
D
E
证法二
证法三
三角形角的关系
三角形按角分类
直角三角形
斜三角形
三角形的内角和等于 180°
锐角三角形
钝角三角形
三角形内角和定理的证明及推论1、2
三角形内角和定理的证明
推论1:直角三角形的两锐角互余.
推论2:有两个角互余的三角形是直角三角形.
三角形的外角
外角:三角形的一边与另一边的延长线所组成的角,叫做三角形的外角.
推论3:三角形的外角等于与它不相邻的两个内角的和.
推论4:三角形的外角大于与它不相邻的任何一个内角.
三角形的外角和等于360°.
①三角形有三条边,三个内角,三个顶点;
②组成三角形的线段叫做三角形的边;
③相邻两边所组成的角叫做三角形内角,简称角;
④相邻两边的公共端点是三角形的顶点;
⑤三角形 ABC 用符号表示为△ABC;
⑥三角形 ABC 的边 AB 可用边 AB 所对的角 C 的小写字母 c 表示,AC 可用 b 表示,BC 可用 a 表示.
A
B
C
不在同一直线上的三条线段首尾依次相接组成的图形叫做三角形.
一、三角形的相关概念
注意:
1.三边关系的依据是:两点之间线段最短.
2.判断三条线段能否构成三角形的方法:只要满足较小的两条线段之和大于第三条线段,便可构成三角形;若不满足,则不能构成三角形.
3.三角形第三边的取值范围是:
两边之差<第三边<两边之和
三角形的任意两边之和大于第三边;
三角形的任意两边之差小于第三边.
二、三角形的三边关系
1. 三角形的高:从三角形的一个顶点向它的对边所在 的直线作垂线,顶点和垂足之间的线段.
表示法:① AD 是△ABC 的边 BC 上的高;
② AD⊥BC 于 D;③∠ADB =∠ADC = 90°.
三、三角形的高、中线、角平分线:
注意:① 三角形的高是线段;
② 锐角三角形三条高全在三角形的内部;
直角三角形有两条高是直角边,另一条在内部;
钝角三角形有两条高在三角形外,另一条在内部.
③ 三角形三条高所在直线交于一点.
注意:①三角形的中线是线段;
②三角形三条中线全在三角形的内部;
③三角形三条中线交于三角形内部一点;
④中线把三角形分成两个面积相等的三角形.
2.三角形的中线:连接一个顶点和它对边中点的线段.
表示法:
① AD 是△ABC 的边 BC 上的中线;
② BD = DC = BC.
注意:①三角形的角平分线是线段;
②三角形三条角平分线全在三角形的内部;
③三角形三条角平分线交于三角形内部一点;
④用量角器画三角形的角平分线.
3. 三角形的角平分线:三角形一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段.
表示法:
① AD 是△ABC 中∠BAC 的平分线.
② ∠1 =∠2 = ∠BAC.
1
2
(
(
注意:① 命题有真命题和假命题两种.
对某一事件作出正确或不正确判断的语句叫做命题.
② 命题由题设和结论两部分组成. 前一部分称之为条件,后一部分称之为结论.
③ 命题通常是用“如果······ 那么······”的形式给出.
④ “如果 p,那么 q”中的题设与结论互换,得一个新命题:“如果 q,那么 p” 这两个命题称为互逆命题.其中一个命题叫做原命题,另一个命题叫做逆命题.
四、命题与证明
⑤ 当一个命题是真命题时它的逆命题不一定是真命题.
⑥ 符合命题的题设,但不满足命题的结论的例子,称之为反例. 要说明一个命题是假命题,只要举一个反例即可.
三角形的内角和定理:三角形的内角和等于 180°.
(2) 从剪拼可以看出:∠A +∠B +∠C = 180°
(1) 从折叠可以看出:∠A +∠B +∠C = 180°
(3) 由推理证明可知:∠A +∠B +∠C = 180°
2. 三角形内角和定理及推论
三角形的外角的定义:由三角形一边与另一边的延长线组成的角,叫做三角形的外角.
三角形的外角与内角的关系:
2.三角形的一个外角等于与它不相邻的两个内角的和;
1.三角形的一个外角与它相邻的内角互补;
3.三角形的一个外角大于任何一个与它不相邻的内角;
4.三角形的外角和为 360°.
考点一 三角形的三边关系
例1 已知两条线段的长分别是 3 cm、8 cm ,要想拼成一个三角形,且第三条线段 a 的长为奇数,问第三条线段应取多长?
解:由三角形两边之和大于第三边,两边之差小于
第三边,得 8 - 3<a<8 + 3,
∴ 5<a<11.
又∵第三边长为奇数,
∴ 第三条边长为 7 cm 或 9 cm.
三角形两边之和大于第三边,可以用来判断三条线段能否组成三角形,在运用中一定要注意检查是否任意两边的和都大于第三边,也可以直接检查较小两边之和是否大于第三边.三角形的三边关系在求线段的取值范围以及在证明线段的不等关系中有着重要的作用.
方法总结
2.在等腰三角形 ABC 中,它的两边长分别为 8 cm 和3 cm,则它的周长为________cm.
1.已知四组线段的长分别如下,以各组线段为边,能组成三角形的是( )
A.1,2,3 B.2,5,8
C.3,4,5 D.4,5,10
C
针对训练
19
3.以线段 3、4、x - 5 为边组成三角形,那么 x 的取值范围是 .
6<x<12
考点二 三角形内角和定理及推论
例2 下列条件中,能判定△ABC 为直角三角形的是 ( )
A.∠A = 2∠B = 3∠C B.∠A +∠B = 2∠C
C.∠A =∠B = 30° D.∠A = ∠B = ∠C
【分析】根据“三角形内角和定理和为180°”求出各选项中△ABC 的内角,然后根据直角三角形的判定方法进行判断.【答案】故选 D.
D
三角形内角和定理:三角形内角和是 180°.其推论为直角三角形两锐角互补及有两个角的和为 90° 的三角形是直角三角形.已知三角形中的三角形之间关系,可运用方程思想来求各角的度数.
方法总结
针对训练
4. 在一个直角三角形中,有一个锐角等于 60°,则另一个锐角的度数为_____.
30°
△ABC 中,∠B = ∠A = ∠C,求△ABC 的三个内角度数.
解:设∠B = x° ,则∠A = 3x°,∠C = 4x°,
从而 x + 3x + 4x = 180°,
解得 x = 22.5°.
即∠B = 22.5°,∠A = 67.5°,∠C = 90°.
考点三 三角形的角平分线、中线和高
例3 下列说法错误的是( )
A.三角形的三条中线都在三角形内,且平分三角形面积
B.直角三角形的高线只有一条
C.三角形的三条角平分线都在三角形内
D.钝角三角形内只有一条高线
B
【分析】根据三角形的角平分线、中线和高的概念逐一进行判断.【答案】B
三角形的三条角平分线、三条中线、三条高 (或延长线) 分别相交于一点,其中中线平分三角形面积,直角三角形有两条高线在直角边上,钝角三角形有两条高在三角形的外面.
方法总结
针对训练
6. 如图所示,AD 是△ABC 的中线,已知△ABD 比△ACD 的周长大 6 cm,则 AB 与 AC 的差为( )
A. 12 cm B. 6 cm
C. 3 cm D. 2 cm
B
A
B
C
D
7. 如图,在△ABC 中,∠ABC ,∠ACB 的平分线 BD,
CE 交于点 O.
(1) 若∠A = 80°,则∠BOC = .
(2) 你能猜想出∠BOC 与∠A 之间的数量关系吗?
130°
∠BOC = 90° + ∠A
A
B
C
O
E
D
例4 分别写出下列命题的条件及结论,并判断真假,是假命题的举出反例.
(1)如果两个角相等,那么它们是对顶角;
(2)如果 a>b,b>c,那么 a>c;
(3)三角形的中线平分该三角形的面积.
考点四 命题与证明
【分析】先把各个命题写成“如果……那么……”的形式,方便找出条件及结论.
解:(1) 条件:两个角相等,结论:它们是对顶角.
假命题,反例:两个角也有可能是两条平行线的同位角或内错角.
(2) 条件: a>b,b>c,结论: a>c,真命题.
(3) 条件:三角形的一条中线分三角形为两个小三角形,结论:这两个小三角形面积相等. 真命题.
方法总结
说明假命题的方法:
举反例
使之具有命题的条件,而不具有命题的结论.
∵直线 AB 与直线 CD 相交于点 O (已知),
8. 如图,直线 AB 与直线 CD 相交于点 O,∠AOC 与∠BOD 是对顶角. 求证:∠AOC =∠BOD.
证明:
∴ ∠AOB 与∠COD 都是平角(平角的定义).
∴ ∠AOC+∠AOD=180°,
∴ ∠AOC =∠BOD(同角的补角相等) .
∠BOD+∠AOD=180°(补角的定义) .
针对训练
例5 如图,求证:∠A +∠B +∠C =∠ADC.
考点五 三角形的外角
【分析】作射线 BD.通过三角形外角的性质进行转化即可求证.
证明:如图,作射线 BD.
A
B
C
D
E
)
)
)
)
1
2
3
4
根据三角形外角的性质,
则有∠3 =∠1 +∠A ①,∠4 =∠2 +∠C ②.
由① + ②得∠3 +∠4 =∠1 +∠A +∠2 +∠C,
故∠A+∠B+∠C =∠ADC 得证.
这是一个常见的几何图形模型,因为它像飞镖,故称之为“飞镖模型”.它利用三角形外角的性质推出四角之间的数量关系,即∠A +∠B +∠C =∠ADC.运用这一结论,能提高我们解题的准确性和速度.
方法总结
其他证法:如图
A
B
C
D
A
B
C
D
E
证法二
证法三
三角形角的关系
三角形按角分类
直角三角形
斜三角形
三角形的内角和等于 180°
锐角三角形
钝角三角形
三角形内角和定理的证明及推论1、2
三角形内角和定理的证明
推论1:直角三角形的两锐角互余.
推论2:有两个角互余的三角形是直角三角形.
三角形的外角
外角:三角形的一边与另一边的延长线所组成的角,叫做三角形的外角.
推论3:三角形的外角等于与它不相邻的两个内角的和.
推论4:三角形的外角大于与它不相邻的任何一个内角.
三角形的外角和等于360°.
