第14章 全等三角形 小结与复习课件(共24张PPT)
文档属性
| 名称 | 第14章 全等三角形 小结与复习课件(共24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 602.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-07 00:00:00 | ||
图片预览


文档简介
(共24张PPT)
能够完全重合的两个图形叫全等形,能够完全重合的两个三角形叫全等三角形.
把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,
重合的角叫做对应角.
重合的边叫做对应边,
一、全等三角形的性质
B
C
E
F
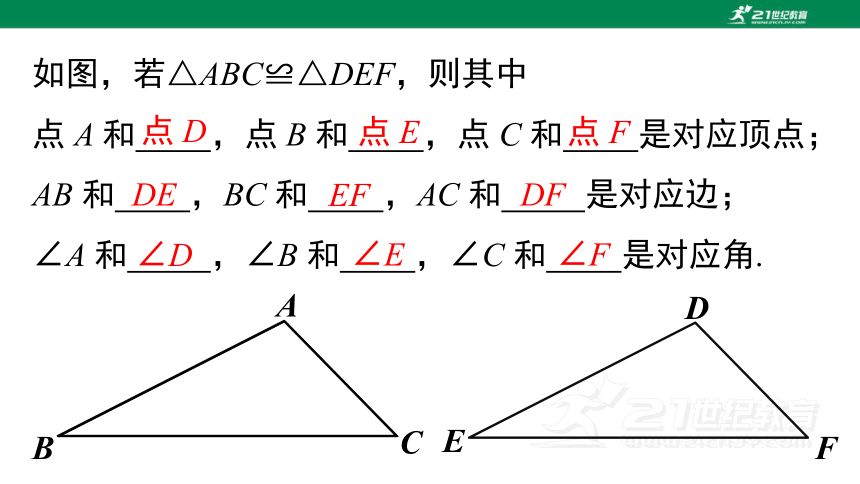
如图,若△ABC≌△DEF,则其中
点 A 和 ,点 B 和 ,点 C 和 是对应顶点;
AB 和 ,BC 和 ,AC 和 是对应边;
∠A 和 ,∠B 和 ,∠C 和 是对应角.
A
D
点 D
点 E
点 F
DE
EF
DF
∠D
∠E
∠F
A
B
C
D
E
F
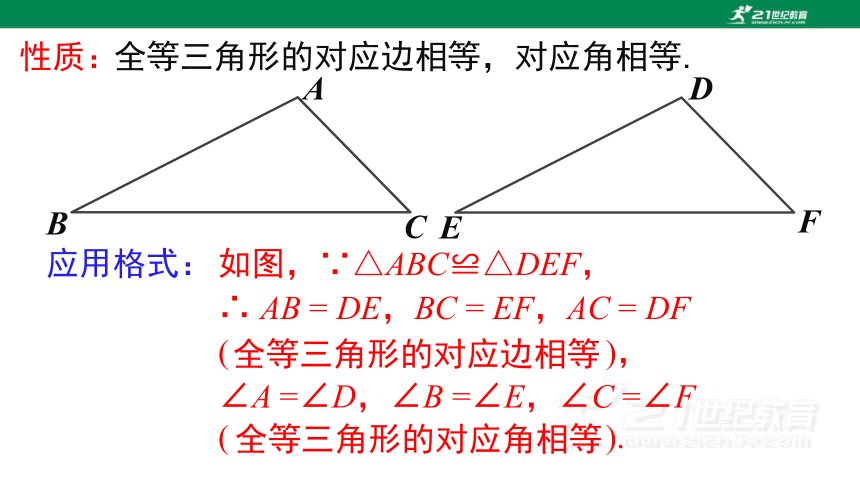
性质:
全等三角形的对应边相等,对应角相等.
如图,∵△ABC≌△DEF,
∴ AB = DE,BC = EF,AC = DF
( ),
∠A =∠D,∠B =∠E,∠C =∠F
( ).
全等三角形的对应边相等
全等三角形的对应角相等
应用格式:
用符号语言表示为:
在△ABC 与△DEF 中,
∴△ABC≌△DEF (SAS).
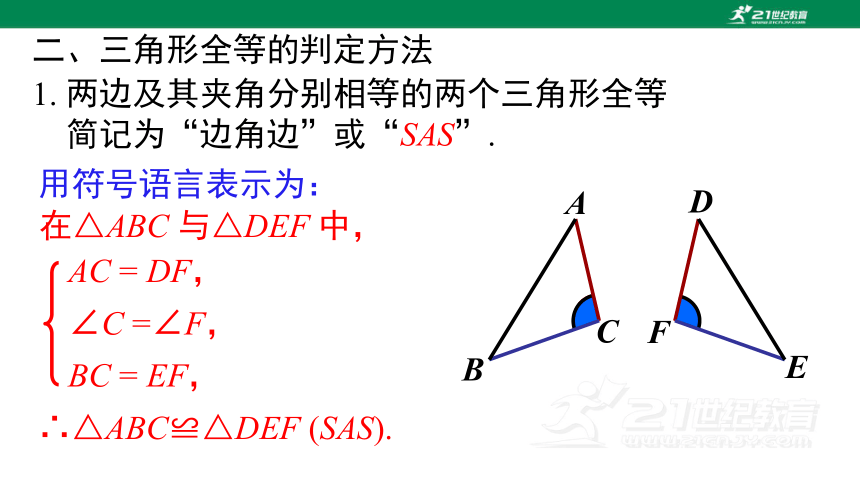
1. 两边及其夹角分别相等的两个三角形全等
简记为“边角边”或“SAS”.
F
E
D
C
B
A
AC = DF,
∠C =∠F,
BC = EF,
二、三角形全等的判定方法
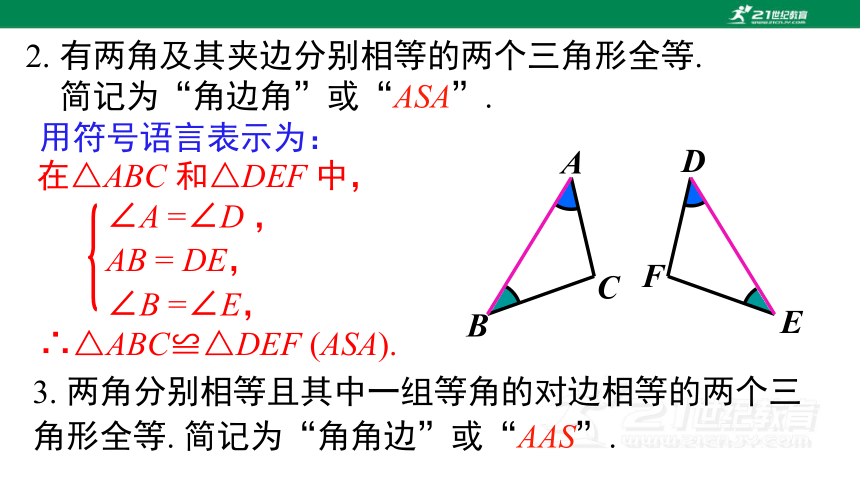
∠A =∠D ,
AB = DE,
∠B =∠E,
在△ABC 和△DEF 中,
∴△ABC≌△DEF (ASA).
2. 有两角及其夹边分别相等的两个三角形全等.
简记为“角边角”或“ASA”.
用符号语言表示为:
F
E
D
C
B
A
3. 两角分别相等且其中一组等角的对边相等的两个三角形全等. 简记为“角角边”或“AAS”.
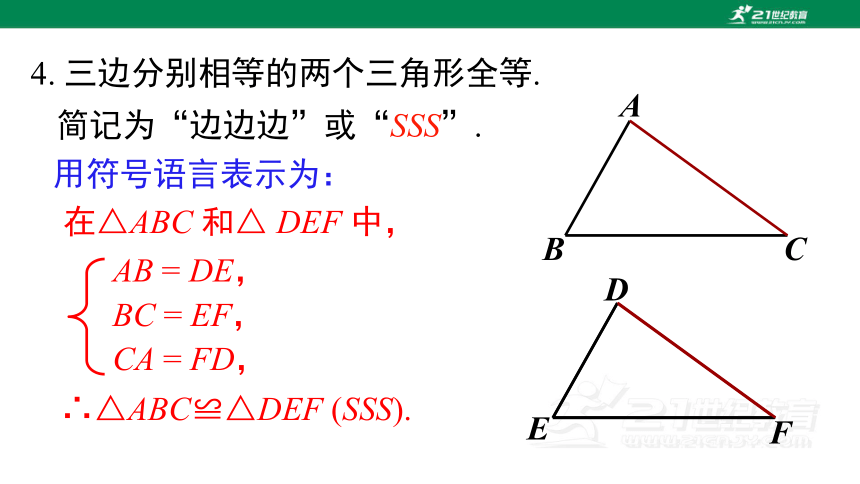
4. 三边分别相等的两个三角形全等.
简记为“边边边”或“SSS”.
A
B
C
在△ABC 和△ DEF 中,
∴△ABC≌△DEF (SSS).
AB = DE,
BC = EF,
CA = FD,
用符号语言表示为:
D
E
F
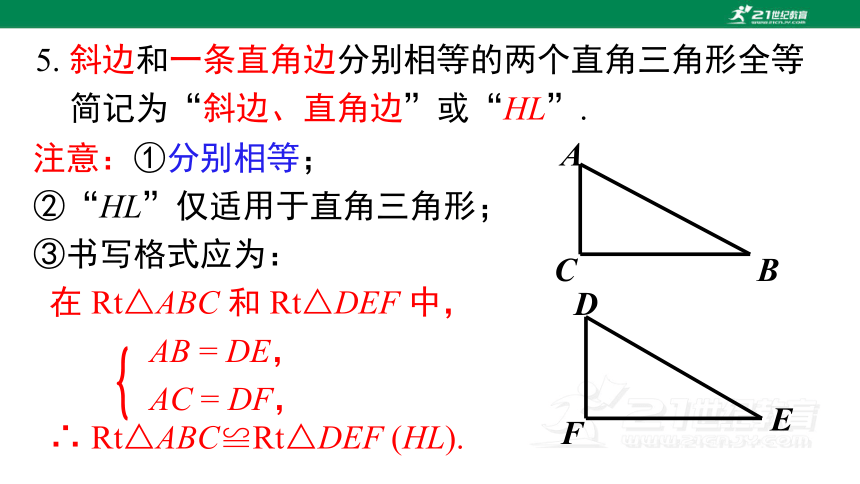
5. 斜边和一条直角边分别相等的两个直角三角形全等
简记为“斜边、直角边”或“HL”.
A
B
C
D
E
F
注意:①分别相等;
②“HL”仅适用于直角三角形;
③书写格式应为:
在 Rt△ABC 和 Rt△DEF 中,
AB = DE,
AC = DF,
∴ Rt△ABC≌Rt△DEF (HL).
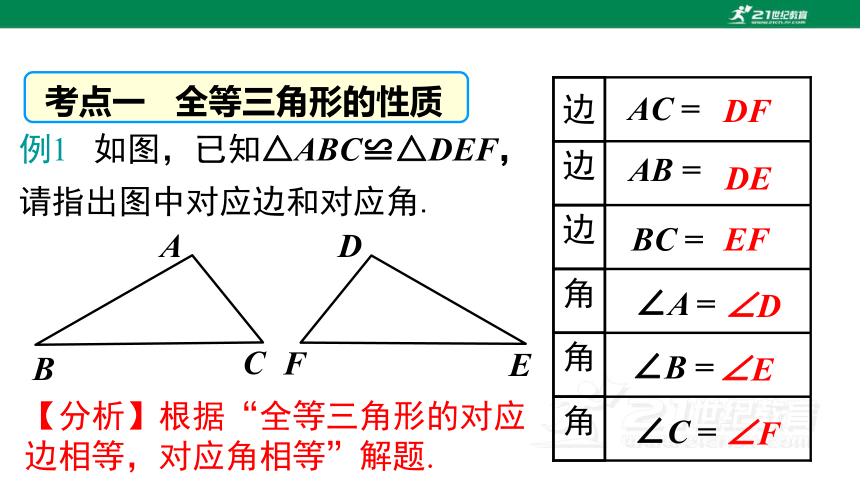
考点一 全等三角形的性质
例1 如图,已知△ABC≌△DEF,请指出图中对应边和对应角.
A
B
C
F
D
E
DF
DE
EF
∠D
∠E
∠F
角
角
角
边
边
边
AC =
AB =
BC =
∠A =
∠B =
∠C =
【分析】根据“全等三角形的对应边相等,对应角相等”解题.
两个全等三角形的长边与长边,短边与短边分别是对应边,大角与大角,小角与小角分别是对应角;有对顶角的,两个对顶角一般是一对对应角;有公共边的,公共边一般是对应边;有公共角的,公共角一般是对应角.
方法总结
A
B
C
E
D
1. 如图,已知△ABC≌△AED,若 AB=6,AC=2,∠B=25°,你还能说出△ADE 中其他角的大小和边的长度吗?
解:∵△ABC≌△AED,
∴∠E = ∠B = 25°
(全等三角形对应角相等),
AC = AD = 2,AB = AE = 6
(全等三角形对应边相等).
针对训练
例2 已知∠ABC=∠DCB,∠ACB=∠DBC.
求证:△ABC≌△DCB.
∠ABC=∠DCB (已知),
BC=CB (公共边),
∠ACB=∠DBC (已知),
证明:在△ABC 和△DCB 中,
∴△ABC≌△DCB (ASA).
B
C
A
D
分析:运用“两角和它们的夹边分别相等的两个三角形全等”进行判定.
考点二 全等三角形的判定
2. 已知△ABC 和△DEF,下列条件中,不能保证△ABC 和△DEF 全等的是 ( )
A. AB=DE,AC=DF,BC=EF
B. ∠A=∠D,∠B=∠E,AC=DF
C. AB=DE,AC=DF,∠A=∠D
D. AB=DE,BC=EF,∠C=∠F
D
针对训练
3. 如图,AB 与 CD 相交于点 O,OA = OB, 添加条件: ,可得△AOC≌△BOD,理由是 (添加一种合适的情况即可).
A
O
D
C
B
∠C =∠D
AAS
答案不唯一
考点三 全等三角形的性质与判定的综合应用
例3 如图,在△ABC 中,AD 平分∠BAC,CE⊥AD 于点 G,交 AB 于点 E,EF∥BC 交 AC 于点 F.
求证:∠DEC =∠FEC.
A
B
C
D
F
E
G
分析:
欲证∠DEC =∠FEC
由平行线的性质转化为证明∠DEC =∠DCE
只需要证明△DEG≌△DCG
证明:∵ CE⊥AD,∴∠AGE =∠AGC = 90°.
在△AGE 和△AGC 中,
∠AGE =∠AGC,
AG = AG,
∠EAG =∠CAG,
∴△AGE≌△AGC (ASA).
∴ GE = GC.
∵ AD 平分∠BAC,∴∠EAG =∠CAG.
A
B
C
D
F
E
G
在△DGE 和△DGC 中,
EG = CG,
∠EGD =∠CGD,
DG = DG,
∴△DGE≌△DGC (SAS).
∴∠DEG = ∠DCG.
∵ EF∥BC,
∴∠FEC = ∠DCG.
∴∠DEC = ∠FEC.
A
B
C
D
F
E
G
利用全等三角形证明角相等,首先要找到两个角所在的两个三角形,看它们全等的条件够不够;有时会用到等角转换,等角转换的途径很多,如:余角,补角的性质、平行线的性质等,必要时需添加辅助线.
方法总结
4. 如图,OB⊥AB,OC⊥AC,垂足为 B,C,OB = OC,那么∠BAO =∠CAO 吗?为什么?
O
C
B
A
解:∠BAO =∠CAO. 理由如下:
∵ OB⊥AB,OC⊥AC,
∴∠B =∠C = 90°.
在 Rt△ABO 和 Rt△ACO 中,
AO = AO,
OB = OC,
∴ Rt△ABO≌Rt△ACO (HL).
∴∠BAO =∠CAO.
针对训练
考点四 利用全等三角形解决实际问题
例4 如图,两根长均为 12 米的绳子一端系在旗杆上,旗杆与地面垂直,另一端分别固定在地面上的木桩上,两根木桩离旗杆底部的距离相等吗?
A
B
C
D
分析:将本题中的实际问题转化为数学问题就是证明 BD = CD. 由已知条件可知 AB = AC,AD⊥BC.
A
B
C
D
解:相等. 理由如下:
∵ AD⊥BC,
∴∠ADB =∠ADC = 90°.
在 Rt△ADB 和 Rt△ADC 中,
AD = AD,
AB = AC,
∴ Rt△ADB≌Rt△ADC (HL).
∴ BD = CD.
利用全等三角形可以测量一些不易测量的距离和长度,还可对某些因素作出判断,一般采用以下步骤:
(1)先明确实际问题;
(2)根据实际抽象出几何图形;
(3)经过分析,找出证明途径;
(4)书写证明过程.
方法总结
针对训练
5. 如图,有一湖的湖岸在 A、B 之间呈一段圆弧状,A、B 间的距离不能直接测得.你能用已学过的知识或方法设计测量方案,求出 A、B 间的距离吗?
解:要测量 A、B 间的距离,可用如下方法:过点 B 作 AB 的垂线 BF,在 BF 上取两点 C、D,使 CD = BC,再作出 BD 的垂线 DE,使 A、C、E 在一条直线上.
在△ABC 和△EDC 中,
∠ACB =∠ECD,
CB = CD,
∠ABC =∠EDC,
∴△ABC≌△EDC(ASA).
∴ BA = DE.
故测出 DE 的长就等于 A、B 间的距离.
C
D
E
F
全等
三角形
性质
基本性质和其他重要性质
判定
判定方法基本思路
作用
是证明两条线段相等和角相等的常用方法
寻找现有条件(包括图中隐含条件)
选定判定方法,证明准备条件
能够完全重合的两个图形叫全等形,能够完全重合的两个三角形叫全等三角形.
把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,
重合的角叫做对应角.
重合的边叫做对应边,
一、全等三角形的性质
B
C
E
F
如图,若△ABC≌△DEF,则其中
点 A 和 ,点 B 和 ,点 C 和 是对应顶点;
AB 和 ,BC 和 ,AC 和 是对应边;
∠A 和 ,∠B 和 ,∠C 和 是对应角.
A
D
点 D
点 E
点 F
DE
EF
DF
∠D
∠E
∠F
A
B
C
D
E
F
性质:
全等三角形的对应边相等,对应角相等.
如图,∵△ABC≌△DEF,
∴ AB = DE,BC = EF,AC = DF
( ),
∠A =∠D,∠B =∠E,∠C =∠F
( ).
全等三角形的对应边相等
全等三角形的对应角相等
应用格式:
用符号语言表示为:
在△ABC 与△DEF 中,
∴△ABC≌△DEF (SAS).
1. 两边及其夹角分别相等的两个三角形全等
简记为“边角边”或“SAS”.
F
E
D
C
B
A
AC = DF,
∠C =∠F,
BC = EF,
二、三角形全等的判定方法
∠A =∠D ,
AB = DE,
∠B =∠E,
在△ABC 和△DEF 中,
∴△ABC≌△DEF (ASA).
2. 有两角及其夹边分别相等的两个三角形全等.
简记为“角边角”或“ASA”.
用符号语言表示为:
F
E
D
C
B
A
3. 两角分别相等且其中一组等角的对边相等的两个三角形全等. 简记为“角角边”或“AAS”.
4. 三边分别相等的两个三角形全等.
简记为“边边边”或“SSS”.
A
B
C
在△ABC 和△ DEF 中,
∴△ABC≌△DEF (SSS).
AB = DE,
BC = EF,
CA = FD,
用符号语言表示为:
D
E
F
5. 斜边和一条直角边分别相等的两个直角三角形全等
简记为“斜边、直角边”或“HL”.
A
B
C
D
E
F
注意:①分别相等;
②“HL”仅适用于直角三角形;
③书写格式应为:
在 Rt△ABC 和 Rt△DEF 中,
AB = DE,
AC = DF,
∴ Rt△ABC≌Rt△DEF (HL).
考点一 全等三角形的性质
例1 如图,已知△ABC≌△DEF,请指出图中对应边和对应角.
A
B
C
F
D
E
DF
DE
EF
∠D
∠E
∠F
角
角
角
边
边
边
AC =
AB =
BC =
∠A =
∠B =
∠C =
【分析】根据“全等三角形的对应边相等,对应角相等”解题.
两个全等三角形的长边与长边,短边与短边分别是对应边,大角与大角,小角与小角分别是对应角;有对顶角的,两个对顶角一般是一对对应角;有公共边的,公共边一般是对应边;有公共角的,公共角一般是对应角.
方法总结
A
B
C
E
D
1. 如图,已知△ABC≌△AED,若 AB=6,AC=2,∠B=25°,你还能说出△ADE 中其他角的大小和边的长度吗?
解:∵△ABC≌△AED,
∴∠E = ∠B = 25°
(全等三角形对应角相等),
AC = AD = 2,AB = AE = 6
(全等三角形对应边相等).
针对训练
例2 已知∠ABC=∠DCB,∠ACB=∠DBC.
求证:△ABC≌△DCB.
∠ABC=∠DCB (已知),
BC=CB (公共边),
∠ACB=∠DBC (已知),
证明:在△ABC 和△DCB 中,
∴△ABC≌△DCB (ASA).
B
C
A
D
分析:运用“两角和它们的夹边分别相等的两个三角形全等”进行判定.
考点二 全等三角形的判定
2. 已知△ABC 和△DEF,下列条件中,不能保证△ABC 和△DEF 全等的是 ( )
A. AB=DE,AC=DF,BC=EF
B. ∠A=∠D,∠B=∠E,AC=DF
C. AB=DE,AC=DF,∠A=∠D
D. AB=DE,BC=EF,∠C=∠F
D
针对训练
3. 如图,AB 与 CD 相交于点 O,OA = OB, 添加条件: ,可得△AOC≌△BOD,理由是 (添加一种合适的情况即可).
A
O
D
C
B
∠C =∠D
AAS
答案不唯一
考点三 全等三角形的性质与判定的综合应用
例3 如图,在△ABC 中,AD 平分∠BAC,CE⊥AD 于点 G,交 AB 于点 E,EF∥BC 交 AC 于点 F.
求证:∠DEC =∠FEC.
A
B
C
D
F
E
G
分析:
欲证∠DEC =∠FEC
由平行线的性质转化为证明∠DEC =∠DCE
只需要证明△DEG≌△DCG
证明:∵ CE⊥AD,∴∠AGE =∠AGC = 90°.
在△AGE 和△AGC 中,
∠AGE =∠AGC,
AG = AG,
∠EAG =∠CAG,
∴△AGE≌△AGC (ASA).
∴ GE = GC.
∵ AD 平分∠BAC,∴∠EAG =∠CAG.
A
B
C
D
F
E
G
在△DGE 和△DGC 中,
EG = CG,
∠EGD =∠CGD,
DG = DG,
∴△DGE≌△DGC (SAS).
∴∠DEG = ∠DCG.
∵ EF∥BC,
∴∠FEC = ∠DCG.
∴∠DEC = ∠FEC.
A
B
C
D
F
E
G
利用全等三角形证明角相等,首先要找到两个角所在的两个三角形,看它们全等的条件够不够;有时会用到等角转换,等角转换的途径很多,如:余角,补角的性质、平行线的性质等,必要时需添加辅助线.
方法总结
4. 如图,OB⊥AB,OC⊥AC,垂足为 B,C,OB = OC,那么∠BAO =∠CAO 吗?为什么?
O
C
B
A
解:∠BAO =∠CAO. 理由如下:
∵ OB⊥AB,OC⊥AC,
∴∠B =∠C = 90°.
在 Rt△ABO 和 Rt△ACO 中,
AO = AO,
OB = OC,
∴ Rt△ABO≌Rt△ACO (HL).
∴∠BAO =∠CAO.
针对训练
考点四 利用全等三角形解决实际问题
例4 如图,两根长均为 12 米的绳子一端系在旗杆上,旗杆与地面垂直,另一端分别固定在地面上的木桩上,两根木桩离旗杆底部的距离相等吗?
A
B
C
D
分析:将本题中的实际问题转化为数学问题就是证明 BD = CD. 由已知条件可知 AB = AC,AD⊥BC.
A
B
C
D
解:相等. 理由如下:
∵ AD⊥BC,
∴∠ADB =∠ADC = 90°.
在 Rt△ADB 和 Rt△ADC 中,
AD = AD,
AB = AC,
∴ Rt△ADB≌Rt△ADC (HL).
∴ BD = CD.
利用全等三角形可以测量一些不易测量的距离和长度,还可对某些因素作出判断,一般采用以下步骤:
(1)先明确实际问题;
(2)根据实际抽象出几何图形;
(3)经过分析,找出证明途径;
(4)书写证明过程.
方法总结
针对训练
5. 如图,有一湖的湖岸在 A、B 之间呈一段圆弧状,A、B 间的距离不能直接测得.你能用已学过的知识或方法设计测量方案,求出 A、B 间的距离吗?
解:要测量 A、B 间的距离,可用如下方法:过点 B 作 AB 的垂线 BF,在 BF 上取两点 C、D,使 CD = BC,再作出 BD 的垂线 DE,使 A、C、E 在一条直线上.
在△ABC 和△EDC 中,
∠ACB =∠ECD,
CB = CD,
∠ABC =∠EDC,
∴△ABC≌△EDC(ASA).
∴ BA = DE.
故测出 DE 的长就等于 A、B 间的距离.
C
D
E
F
全等
三角形
性质
基本性质和其他重要性质
判定
判定方法基本思路
作用
是证明两条线段相等和角相等的常用方法
寻找现有条件(包括图中隐含条件)
选定判定方法,证明准备条件
