八下期末复习——第四、五单元提升卷(含解析)
文档属性
| 名称 | 八下期末复习——第四、五单元提升卷(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 717.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-06 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
八下期末复习第四、五单元提升卷(含解析)
一、单选题
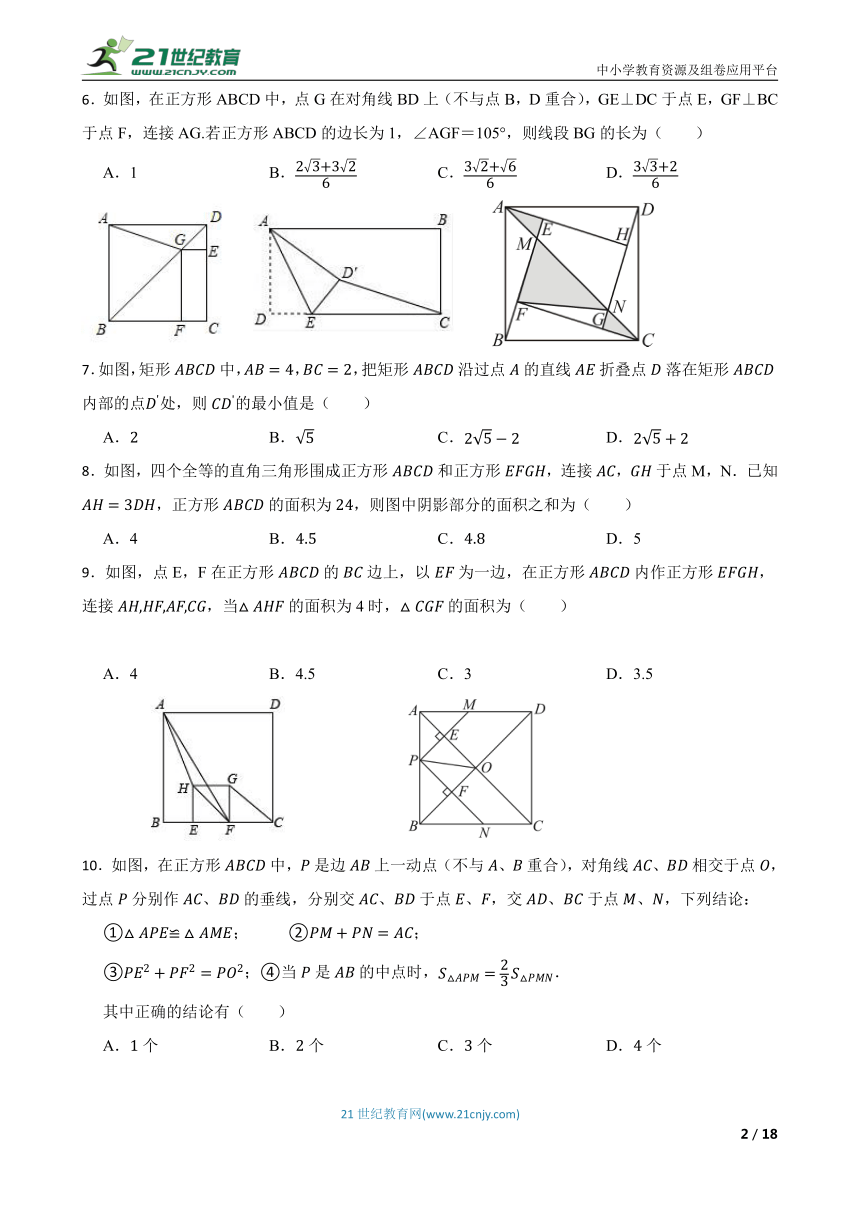
1.如图,在矩形ABCD中,连接BD,分别以B、D为圆心,大于的长为半径画弧,两弧交于P、Q两点,作直线PQ,分别与AD、BC交于点M、N,连接BM、DN.若,.则四边形MBND的周长为( )
A. B.5 C.10 D.20
2.如图,在中,平分,是的中点,,,,则的长为( )
A.1 B. C.2 D.
3.如图,正方形的边长为2,连接、,平分交于点E,则的长是( ).
A. B. C. D.
4.如图,在中,,,,按如下步骤作图:
①分别以点,为圆心,以大于的长为半径在两边作弧,交于两点,;②作直线,分别交,于点,;③过作 交于点,连接,.则四边形的周长为( )
A. B. C. D.
5.如图,矩形ABCD中,AB=8,AD=4,点E、F分别是AB、DC上的动点,EF∥BC,则AF+CE的最小值是( )
A.8 B.12 C.8 D.16
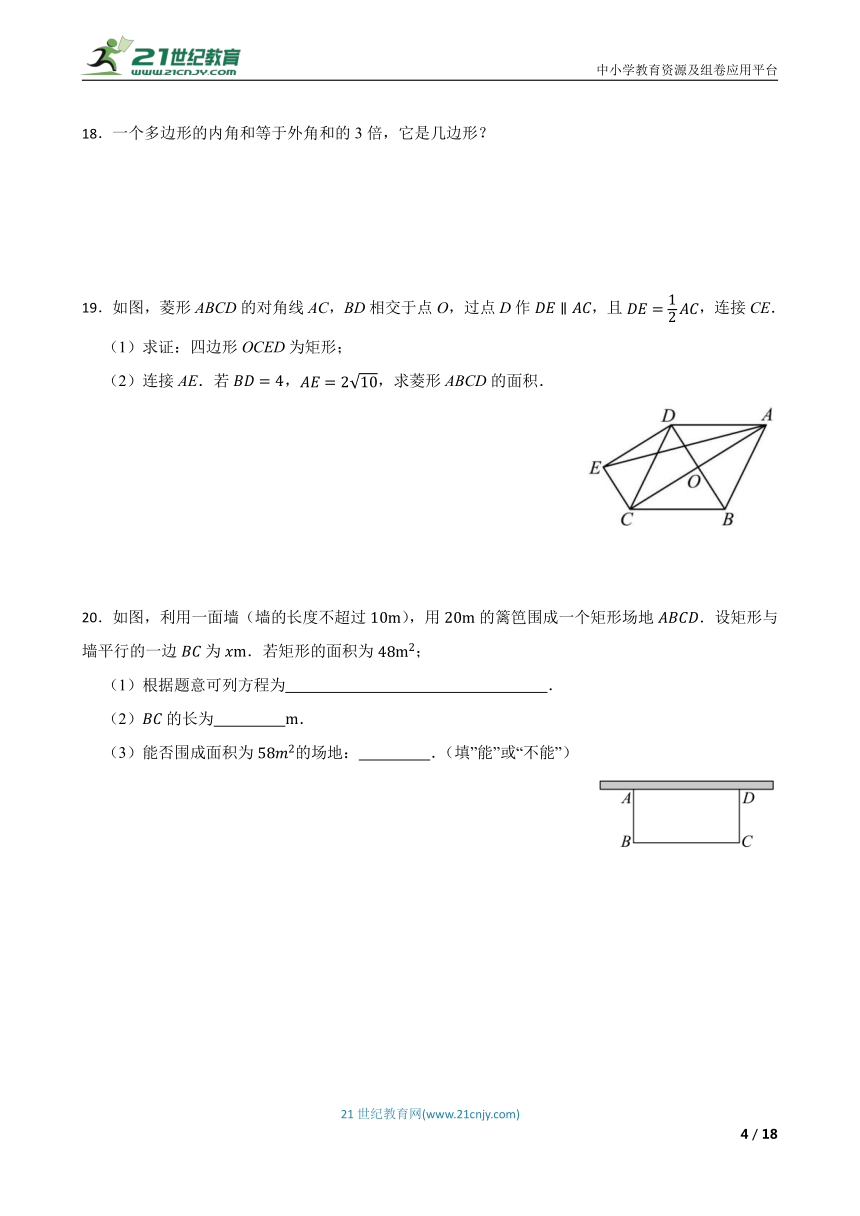
6.如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连接AG.若正方形ABCD的边长为1,∠AGF=105°,则线段BG的长为( )
A.1 B. C. D.
7.如图,矩形中,,,把矩形沿过点的直线折叠点落在矩形内部的点处,则的最小值是( )
A. B. C. D.
8.如图,四个全等的直角三角形围成正方形和正方形,连接,于点M,N.已知,正方形的面积为,则图中阴影部分的面积之和为( )
A.4 B. C. D.5
9.如图,点E,F在正方形的边上,以为一边,在正方形内作正方形,连接,当的面积为4时,的面积为( )
A.4 B.4.5 C.3 D.3.5
10.如图,在正方形中,是边上一动点(不与、重合),对角线、相交于点,过点分别作、的垂线,分别交、于点、,交、于点、,下列结论:
①; ②;
③;④当是的中点时,.
其中正确的结论有( )
A.个 B.个 C.个 D.个
二、填空题
11.如图,在 ABCD中,AE平分∠BAD交BC于点E,连接AC.若AB=AE,∠EAC=20°,则∠ACD的度数为 .
12.如图,在边长为4的等边三角形的外侧作正方形,过点D作,垂足为F,则的长为.
13.如图是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形.如果AB=13,EF=7,那么AH等于 。
14.如图,矩形的面积为1,它的两条对角线交于点,以、为两邻边作平行四边形,平行四边形,的对角线交于点,同样以、为两邻边作平行四边形,依次类推,则平行四边形的面积为
15.如图,已知,正中,,将沿翻折,得到,连接,交于点,点在上,且,是的中点,是上的一个动点,则的最大值为 .
16.如图,在正方形ABCD中,点P是AB上一动点(不与A、B重合),对角线AC、BD相交于点O,过点P分别作AC、BD的垂线,分别交AC、BD于点E、F,交AD、BC于点M、N.下列结论:①△APE≌△AME;②PM+PN=AC;③PE2+PF2=PO2;④△POF∽△BNF;⑤点O在M、N两点的连线上.其中正确的是 .
三、解答题
17.请你经过点A作一条直线使五边形化为与之面积相等的四边形。
、
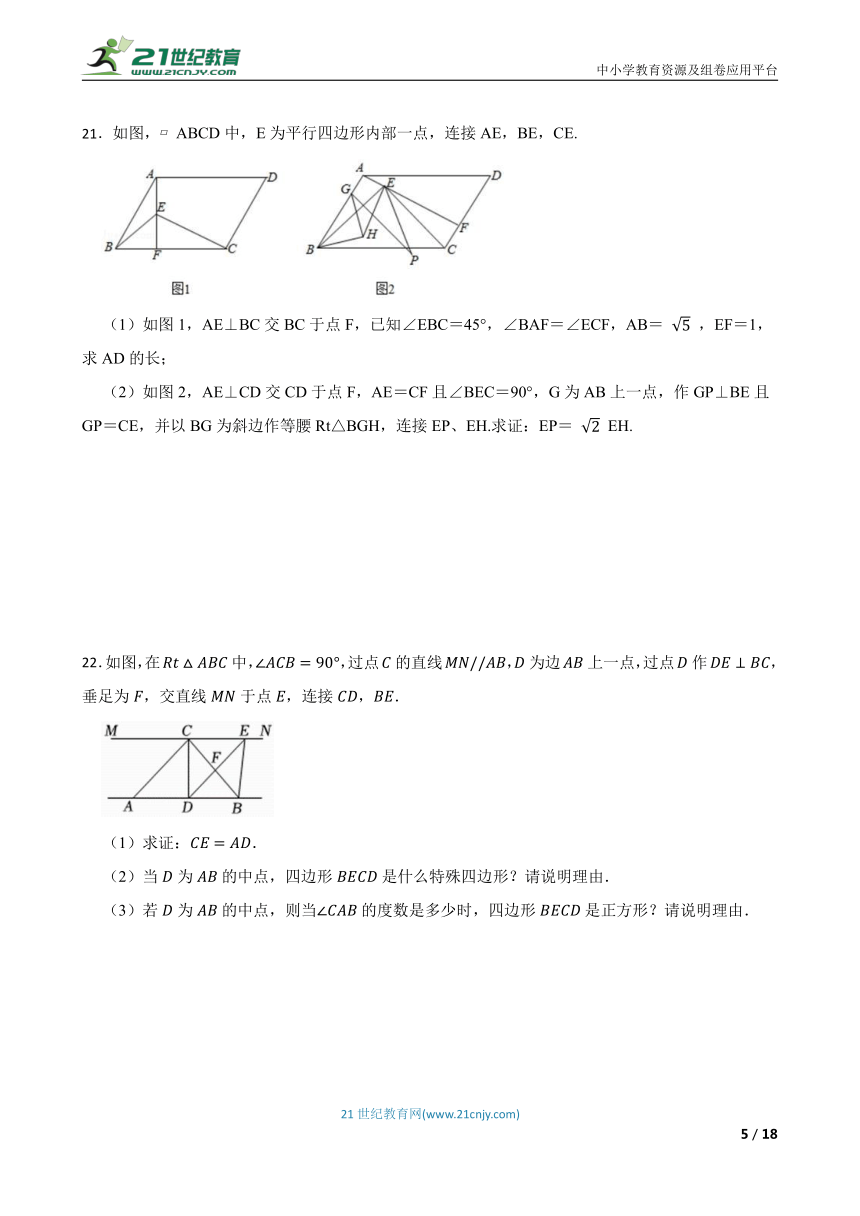
18.一个多边形的内角和等于外角和的3倍,它是几边形?
19.如图,菱形ABCD的对角线AC,BD相交于点O,过点D作,且,连接CE.
(1)求证:四边形OCED为矩形;
(2)连接AE.若,,求菱形ABCD的面积.
20.如图,利用一面墙(墙的长度不超过),用的篱笆围成一个矩形场地.设矩形与墙平行的一边为.若矩形的面积为;
(1)根据题意可列方程为 .
(2)的长为 .
(3)能否围成面积为的场地: .(填”能”或“不能”)
21.如图, ABCD中,E为平行四边形内部一点,连接AE,BE,CE.
(1)如图1,AE⊥BC交BC于点F,已知∠EBC=45°,∠BAF=∠ECF,AB= ,EF=1,求AD的长;
(2)如图2,AE⊥CD交CD于点F,AE=CF且∠BEC=90°,G为AB上一点,作GP⊥BE且GP=CE,并以BG为斜边作等腰Rt△BGH,连接EP、EH.求证:EP= EH.
22.如图,在中,,过点的直线,为边上一点,过点作,垂足为,交直线于点,连接,.
(1)求证:.
(2)当为的中点,四边形是什么特殊四边形?请说明理由.
(3)若为的中点,则当的度数是多少时,四边形是正方形?请说明理由.
23.如图,在 中.点 在 边上,点 在 边上,且 ,连接 、 相交于点 ,连接 、 相交于点.
(1)如图1,求证:四边形 为平行四边形;
(2)如图2,连接 ,若 是 的中点,在不添加任何辅助线的情况下,请直接写出图2中以 为边的所有平行四边形.
24.如图,直线:与坐标轴交于A、B两点,点C与点A关于y轴对称.轴与直线交于点D.
(1)求点A和点B的坐标;
(2)点P在直线上,且的面积为,
①求出点P的坐标;
②点Q为平面内一点,当点P在直线下方时,以点A、B、P、Q为顶点的四边形是平行四边形,请直接写出所有符合要求的点Q坐标.
答案解析部分
1.【答案】C
【解析】【解答】解:四边形是矩形,
,
,
由作图过程可知,垂直平分,
,
,
,
,
四边形是平行四边形,
又,
平行四边形是菱形,
设,则,
在中,,即,
解得,
则四边形的周长为,
故答案为:C.
【分析】根据矩形性质可得,则,再根据垂直平分线性质可得,根据等边对等角可得,则,再根据直线平行判定定理可得,再根据菱形判定定理可得平行四边形是菱形,则设,则,再根据勾股定理建立方程,解方程可得,再根据四边形周长即可求出答案.
2.【答案】A
【解析】【解答】解:延长交的延长线于点,如图,
,
,
平分,
,
,
是等腰三角形,
,点E是的中点,
,是的中位线,
.
故答案为:A.
【分析】延长交的延长线于点,先证出是等腰三角形,再求出,是的中位线,最后利用中位线的性质可得.
3.【答案】D
4.【答案】C
5.【答案】A
【解析】【解答】解:延长BC至G,使CG=EF,连接FG,
∵EF∥CG,EF=CG,
∴四边形EFGC为平行四边形,
∴CE=FG,
∴AF+CE=AF+FG,故当A、F、G共线时,取得最小值AG,
∵AB=8,AD=4,
∴BG=BC+CG=4+4=8,
∴AG=.
故答案为:A.
【分析】延长BC至G,使CG=EF,连接FG,易得四边形EFGC为平行四边形,则CE=FG,AF+CE=AF+FG,故当A、F、G共线时,取得最小值AG,然后在Rt△ABG中,利用勾股定理进行计算.
6.【答案】C
【解析】【解答】解:过A点作AH⊥DB于H点,如图,
∵GE⊥DC,GF⊥BC,
∴,
∵BD为对角线,即∠FBD=∠BDC=45°,
∴∠FGB=∠BDC=∠ABD=45°,
∵∠AGF=105°,
∴∠AGB=60°,
∴在Rt△AHG中,AH=HG,
在正方形ABCD中,AB=1,
∴对角线BD=,
在Rt△AHB中,∠ABD=45°,AB=1,
∴AH=HB=,
∴HG=,
∴BG=BH+HG=,
故答案为:C.
【分析】过A点作AH⊥DB于H点,由GE⊥DC,GF⊥BC可得GF∥CD,由正方形性质∠FGB=∠BDC=∠ABD=45°,BD=,从而求出∠AGB=60°,在Rt△AHG中,可得AH=HG,在等腰Rt△AHB中,可得AH=HB=AB=,继而求出GH,利用BG=BH+GH即可求解.
7.【答案】C
8.【答案】C
9.【答案】A
10.【答案】C
11.【答案】80°
12.【答案】
13.【答案】5
【解析】【解答】∵△ABH≌△BCG≌△CDF≌△DAE,
则AE=BH=CG=DF,AH=BG=CF=DE,
∴EF=FG=GH=HE=7,
设AH=x,
则BH=BG+HG=7+x,
在Rt△AHB中,AB2=AH2+BH2,
132=x2+(7+x)2,
(x-5)(x+7)=0,
解得x=5或x=-12(舍去).
故答案为:5.
【分析】根据三角形全等的性质得对应边分别相等,推得EF=FG=GH=HE=7,设AH=x, 把BH用含x的代数式表示,在△ABH中,利用勾股定理列式求得x即可.
14.【答案】或
15.【答案】
16.【答案】①②③⑤
【解析】【解答】解:∵四边形是正方形,为对角线,
∴,
根据题意,故,
∴,
在三角形与中,
,
∴,故①正确;
∴,
同理,可证,,
∵正方形中,,
又∵,
∴,
∴四边形为矩形,
∴,
∴,
又∵,
,
∴,故②正确;
∵四边形为矩形,
∴,
在直角三角形中,,
∴,故③正确;
∵是等腰直角三角形,而P点是动点,无法保证是等腰直角三角形,
故④错误;
连接,
在和中,
∴,
同理可证,
又∵,
,
∴M,N,P在以O为圆心,为半径的圆上,
又∵,
∴是圆O的直径,
∴点在两点的连线上.故⑤正确.
故答案为: ①②③⑤ .
【分析】①根据题意及正方形的性质,利用ASA判断;
②根据及正方形的性质,得,同理可证,根据题意可证四边形为矩形,则,则,,故证明;
③根据四边形为矩形的性质,在直角三角形中,使用勾股定理,即可判断;
④是等腰直角三角形,而P点是动点,无法保证是等腰直角三角形,故④可判断;
⑤连接,证明,根据直角三角形斜边中线等于斜边一半,即可证明.
17.【答案】解:连接AD,过点E作EF∥AD交CD的延长线于F,连接AF,此时 ,直线AF为所求直线.
理由:∵AD∥EF,
∴ ,
∴ ,
即 ,
∴ .
【解析】【分析】连接AD,过点E作EF∥AD交CD的延长线于F,连接AF,此时 ,进而得到 ,可得 ,则直线AF为所求直线.
18.【答案】解:由题意得,这个多边形的内角和为360°×3=1080°,
设这个多边形的边数为n,
则(n-2)×180°=1080°,
解得:n=8,
即它是八边形.
【解析】【分析】根据多边形的外角和是360度求出这个多边形的内角和,再根据多边形内角和公式计算边数即可.
19.【答案】(1)证明:∵四边形ABCD是菱形,
∴,,
∵,
∴,
∴,
∴四边形OCED为平行四边形,
∵,
∴四边形OCED为矩形;
(2)解:∵四边形OCED为矩形,四边形ABCD是菱形
∴,,
∴,
∴菱形ABCD的面积.
【解析】【分析】(1)根据菱形的性质得到:,,进而得到DE=OC,即可由一组对边平行且相等的四边形是平行四边形证明四边形OCED为平行四边形,进而根据有一个角是直角的平行四边形是矩形证明四边形OCED为矩形;
(2)根据矩形的性质得到:,,进而利用勾股定理求出AC的长度,最后根据菱形的面积等于两对角线乘积的一半即可求出菱形的面积.
20.【答案】或;8;不能
21.【答案】(1)解: 如图1中,
∵AF⊥BC,
∴∠AFB=∠CFE=90°,
∵∠EBC=45°,
∴∠EBF=∠BEF=45°,
∴FB=FE,
∵∠BAF=∠ECF,
∴△AFB≌△CFE(AAS),
∴AF=CF
∵AB= ,
∴AF=CF= =2,
∴BC=BF+CF=3,
∵四边形ABCD是平行四边形,
∴AD=BC=3
(2)证明:如图2中,设PG交BE于T,BE交GH于Q.
∵四边形ABCD是平行四边形,
∴AB∥CD,
∵AF⊥CD,
∴AF⊥AB,
∴∠BAE=∠EFC=90°,
∵∠BEC=90°,
∴∠AEB+∠CEF=90°,∠CEF+∠ECF=90°,
∴∠AEB=∠ECF,
∵AE=CF,
∴△BAE≌△EFC(ASA),
∴BE=EC,
∵GP=EC,
∴GP=BE,
∵GP⊥BE,
∴∠GTQ=90°,
∵BH=GH,∠BHG=90°,
∴∠BHQ=∠GTQ,
∵∠GQT=∠BQH,
∴∠HGP=∠HBE,
∴△EHB≌△PHG(SAS),
∴EH=PH,∠TEO=∠OPH,
∵∠EOT=∠POH,
∴∠PHO=∠ETO=90°,
∴△EHP是等腰直角三角形,
∴PE= EH.
故答案为:(1)AD=3.(2)见解析.
【解析】【分析】(1)首先判断出△BEF是等腰直角三角形,根据等腰直角三角形的性质得出 ∠EBF=∠BEF=45°, FB=FE=1 ,根据勾股定理算出AF的长,然后利用AAS判断出 △AFB≌△CFE ,根据全等三角形的对应边相等得出AF=CF=2,根据线段的和差得出BC的长,根据平行四边形的对边相等得出AD的长;
(2) 如图2中,设PG交BE于T,BE交GH于Q,根据同角的余角相等得出 ∠AEB=∠ECF, 然后利用ASA判断出△BAE≌△EFC ,根据全等三角形的对应边相等得出 BE=EC, 又 GP=EC, 故 GP=BE;然后利用SAS判断出 △EHB≌△PHG ,根据全等三角形的性质得出 EH=PH,∠TEO=∠OPH, 再判断出 △EHP是等腰直角三角形, 根据等腰直角三角形的性质即可得出 PE= EH 。
22.【答案】(1)证明:于点,,
,
.
又,即,
四边形是平行四边形,
.
(2)解:四边形是菱形.
理由:是的中点,
.
又,
四边形是平行四边形.
,
平行四边形是菱形.
(3)解:若为的中点,当时,四边形是正方形.
理由如下:,,
,
.
又是的中点,
,
即.
菱形是正方形.
【解析】【分析】(1)首先根据平行四边形的判定得出四边形是平行四边形,再根据平行四边形对边相等,即可得出结论;
(2)首先证得四边形是平行四边形,再根据对角线垂直,即可得出平行四边形是菱形;
(3)若为的中点,当时,四边形是正方形.由(2)知平行四边形是菱形,再根据等腰三角形CAB中,根据三线合一的性质得出,即可得出 四边形是正方形 .
23.【答案】(1)证明:因为 ,
所以 , ,
又因为 ,
所以四边形AFCE为平行四边形,
所以AF∥CE,
因为AD-AE=BC-CF,即DE=BF,
因为DE∥BF,
所以四边形 为平行四边形,
所以
所以四边形 为平行四边形.
(2)解:以 为边的平行四边形有 、 、 、 .
∵ ,
∴ , ,
∵ 是 的中点,
∴AE=DE= ,
∵ ,
∴CF= ,
∴点F为BC中点,
∴AE=DE=BF=CF,
∴四边形AFCE与四边形EBFD均为平行四边形
∴AF∥EC,EB∥DF,
∴∠EAM=∠DEN,∠AEM=∠EDN,
在△AME和△END中
∴△AME≌△END(ASA)
∴AM=EN,
又∵AM∥EN,
∴四边形AENM为平行四边形,
∴AE∥MN,且AE=MN,
∴ED∥MN,且ED=MN,
∴四边形EDNM为平行四边形,
∴BF∥MN,且BF=MN,
∴四边形BMNF为平行四边形,
∴FC∥MN,且FC=MN,
∴四边形FCNM为平行四边形,
∴以 为边的平行四边形有 、 、 、 .
【解析】【分析】(1)先求出 , , 再求出 DE∥BF, 最后证明求解即可;
(2)先求出 AE=DE= , 再求出 △AME≌△END ,最后证明求解即可。
24.【答案】(1)点、的坐标分别为、
(2)①或;②或或
21世纪教育网(www.21cnjy.com)
八下期末复习第四、五单元提升卷(含解析)
一、单选题
1.如图,在矩形ABCD中,连接BD,分别以B、D为圆心,大于的长为半径画弧,两弧交于P、Q两点,作直线PQ,分别与AD、BC交于点M、N,连接BM、DN.若,.则四边形MBND的周长为( )
A. B.5 C.10 D.20
2.如图,在中,平分,是的中点,,,,则的长为( )
A.1 B. C.2 D.
3.如图,正方形的边长为2,连接、,平分交于点E,则的长是( ).
A. B. C. D.
4.如图,在中,,,,按如下步骤作图:
①分别以点,为圆心,以大于的长为半径在两边作弧,交于两点,;②作直线,分别交,于点,;③过作 交于点,连接,.则四边形的周长为( )
A. B. C. D.
5.如图,矩形ABCD中,AB=8,AD=4,点E、F分别是AB、DC上的动点,EF∥BC,则AF+CE的最小值是( )
A.8 B.12 C.8 D.16
6.如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连接AG.若正方形ABCD的边长为1,∠AGF=105°,则线段BG的长为( )
A.1 B. C. D.
7.如图,矩形中,,,把矩形沿过点的直线折叠点落在矩形内部的点处,则的最小值是( )
A. B. C. D.
8.如图,四个全等的直角三角形围成正方形和正方形,连接,于点M,N.已知,正方形的面积为,则图中阴影部分的面积之和为( )
A.4 B. C. D.5
9.如图,点E,F在正方形的边上,以为一边,在正方形内作正方形,连接,当的面积为4时,的面积为( )
A.4 B.4.5 C.3 D.3.5
10.如图,在正方形中,是边上一动点(不与、重合),对角线、相交于点,过点分别作、的垂线,分别交、于点、,交、于点、,下列结论:
①; ②;
③;④当是的中点时,.
其中正确的结论有( )
A.个 B.个 C.个 D.个
二、填空题
11.如图,在 ABCD中,AE平分∠BAD交BC于点E,连接AC.若AB=AE,∠EAC=20°,则∠ACD的度数为 .
12.如图,在边长为4的等边三角形的外侧作正方形,过点D作,垂足为F,则的长为.
13.如图是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形.如果AB=13,EF=7,那么AH等于 。
14.如图,矩形的面积为1,它的两条对角线交于点,以、为两邻边作平行四边形,平行四边形,的对角线交于点,同样以、为两邻边作平行四边形,依次类推,则平行四边形的面积为
15.如图,已知,正中,,将沿翻折,得到,连接,交于点,点在上,且,是的中点,是上的一个动点,则的最大值为 .
16.如图,在正方形ABCD中,点P是AB上一动点(不与A、B重合),对角线AC、BD相交于点O,过点P分别作AC、BD的垂线,分别交AC、BD于点E、F,交AD、BC于点M、N.下列结论:①△APE≌△AME;②PM+PN=AC;③PE2+PF2=PO2;④△POF∽△BNF;⑤点O在M、N两点的连线上.其中正确的是 .
三、解答题
17.请你经过点A作一条直线使五边形化为与之面积相等的四边形。
、
18.一个多边形的内角和等于外角和的3倍,它是几边形?
19.如图,菱形ABCD的对角线AC,BD相交于点O,过点D作,且,连接CE.
(1)求证:四边形OCED为矩形;
(2)连接AE.若,,求菱形ABCD的面积.
20.如图,利用一面墙(墙的长度不超过),用的篱笆围成一个矩形场地.设矩形与墙平行的一边为.若矩形的面积为;
(1)根据题意可列方程为 .
(2)的长为 .
(3)能否围成面积为的场地: .(填”能”或“不能”)
21.如图, ABCD中,E为平行四边形内部一点,连接AE,BE,CE.
(1)如图1,AE⊥BC交BC于点F,已知∠EBC=45°,∠BAF=∠ECF,AB= ,EF=1,求AD的长;
(2)如图2,AE⊥CD交CD于点F,AE=CF且∠BEC=90°,G为AB上一点,作GP⊥BE且GP=CE,并以BG为斜边作等腰Rt△BGH,连接EP、EH.求证:EP= EH.
22.如图,在中,,过点的直线,为边上一点,过点作,垂足为,交直线于点,连接,.
(1)求证:.
(2)当为的中点,四边形是什么特殊四边形?请说明理由.
(3)若为的中点,则当的度数是多少时,四边形是正方形?请说明理由.
23.如图,在 中.点 在 边上,点 在 边上,且 ,连接 、 相交于点 ,连接 、 相交于点.
(1)如图1,求证:四边形 为平行四边形;
(2)如图2,连接 ,若 是 的中点,在不添加任何辅助线的情况下,请直接写出图2中以 为边的所有平行四边形.
24.如图,直线:与坐标轴交于A、B两点,点C与点A关于y轴对称.轴与直线交于点D.
(1)求点A和点B的坐标;
(2)点P在直线上,且的面积为,
①求出点P的坐标;
②点Q为平面内一点,当点P在直线下方时,以点A、B、P、Q为顶点的四边形是平行四边形,请直接写出所有符合要求的点Q坐标.
答案解析部分
1.【答案】C
【解析】【解答】解:四边形是矩形,
,
,
由作图过程可知,垂直平分,
,
,
,
,
四边形是平行四边形,
又,
平行四边形是菱形,
设,则,
在中,,即,
解得,
则四边形的周长为,
故答案为:C.
【分析】根据矩形性质可得,则,再根据垂直平分线性质可得,根据等边对等角可得,则,再根据直线平行判定定理可得,再根据菱形判定定理可得平行四边形是菱形,则设,则,再根据勾股定理建立方程,解方程可得,再根据四边形周长即可求出答案.
2.【答案】A
【解析】【解答】解:延长交的延长线于点,如图,
,
,
平分,
,
,
是等腰三角形,
,点E是的中点,
,是的中位线,
.
故答案为:A.
【分析】延长交的延长线于点,先证出是等腰三角形,再求出,是的中位线,最后利用中位线的性质可得.
3.【答案】D
4.【答案】C
5.【答案】A
【解析】【解答】解:延长BC至G,使CG=EF,连接FG,
∵EF∥CG,EF=CG,
∴四边形EFGC为平行四边形,
∴CE=FG,
∴AF+CE=AF+FG,故当A、F、G共线时,取得最小值AG,
∵AB=8,AD=4,
∴BG=BC+CG=4+4=8,
∴AG=.
故答案为:A.
【分析】延长BC至G,使CG=EF,连接FG,易得四边形EFGC为平行四边形,则CE=FG,AF+CE=AF+FG,故当A、F、G共线时,取得最小值AG,然后在Rt△ABG中,利用勾股定理进行计算.
6.【答案】C
【解析】【解答】解:过A点作AH⊥DB于H点,如图,
∵GE⊥DC,GF⊥BC,
∴,
∵BD为对角线,即∠FBD=∠BDC=45°,
∴∠FGB=∠BDC=∠ABD=45°,
∵∠AGF=105°,
∴∠AGB=60°,
∴在Rt△AHG中,AH=HG,
在正方形ABCD中,AB=1,
∴对角线BD=,
在Rt△AHB中,∠ABD=45°,AB=1,
∴AH=HB=,
∴HG=,
∴BG=BH+HG=,
故答案为:C.
【分析】过A点作AH⊥DB于H点,由GE⊥DC,GF⊥BC可得GF∥CD,由正方形性质∠FGB=∠BDC=∠ABD=45°,BD=,从而求出∠AGB=60°,在Rt△AHG中,可得AH=HG,在等腰Rt△AHB中,可得AH=HB=AB=,继而求出GH,利用BG=BH+GH即可求解.
7.【答案】C
8.【答案】C
9.【答案】A
10.【答案】C
11.【答案】80°
12.【答案】
13.【答案】5
【解析】【解答】∵△ABH≌△BCG≌△CDF≌△DAE,
则AE=BH=CG=DF,AH=BG=CF=DE,
∴EF=FG=GH=HE=7,
设AH=x,
则BH=BG+HG=7+x,
在Rt△AHB中,AB2=AH2+BH2,
132=x2+(7+x)2,
(x-5)(x+7)=0,
解得x=5或x=-12(舍去).
故答案为:5.
【分析】根据三角形全等的性质得对应边分别相等,推得EF=FG=GH=HE=7,设AH=x, 把BH用含x的代数式表示,在△ABH中,利用勾股定理列式求得x即可.
14.【答案】或
15.【答案】
16.【答案】①②③⑤
【解析】【解答】解:∵四边形是正方形,为对角线,
∴,
根据题意,故,
∴,
在三角形与中,
,
∴,故①正确;
∴,
同理,可证,,
∵正方形中,,
又∵,
∴,
∴四边形为矩形,
∴,
∴,
又∵,
,
∴,故②正确;
∵四边形为矩形,
∴,
在直角三角形中,,
∴,故③正确;
∵是等腰直角三角形,而P点是动点,无法保证是等腰直角三角形,
故④错误;
连接,
在和中,
∴,
同理可证,
又∵,
,
∴M,N,P在以O为圆心,为半径的圆上,
又∵,
∴是圆O的直径,
∴点在两点的连线上.故⑤正确.
故答案为: ①②③⑤ .
【分析】①根据题意及正方形的性质,利用ASA判断;
②根据及正方形的性质,得,同理可证,根据题意可证四边形为矩形,则,则,,故证明;
③根据四边形为矩形的性质,在直角三角形中,使用勾股定理,即可判断;
④是等腰直角三角形,而P点是动点,无法保证是等腰直角三角形,故④可判断;
⑤连接,证明,根据直角三角形斜边中线等于斜边一半,即可证明.
17.【答案】解:连接AD,过点E作EF∥AD交CD的延长线于F,连接AF,此时 ,直线AF为所求直线.
理由:∵AD∥EF,
∴ ,
∴ ,
即 ,
∴ .
【解析】【分析】连接AD,过点E作EF∥AD交CD的延长线于F,连接AF,此时 ,进而得到 ,可得 ,则直线AF为所求直线.
18.【答案】解:由题意得,这个多边形的内角和为360°×3=1080°,
设这个多边形的边数为n,
则(n-2)×180°=1080°,
解得:n=8,
即它是八边形.
【解析】【分析】根据多边形的外角和是360度求出这个多边形的内角和,再根据多边形内角和公式计算边数即可.
19.【答案】(1)证明:∵四边形ABCD是菱形,
∴,,
∵,
∴,
∴,
∴四边形OCED为平行四边形,
∵,
∴四边形OCED为矩形;
(2)解:∵四边形OCED为矩形,四边形ABCD是菱形
∴,,
∴,
∴菱形ABCD的面积.
【解析】【分析】(1)根据菱形的性质得到:,,进而得到DE=OC,即可由一组对边平行且相等的四边形是平行四边形证明四边形OCED为平行四边形,进而根据有一个角是直角的平行四边形是矩形证明四边形OCED为矩形;
(2)根据矩形的性质得到:,,进而利用勾股定理求出AC的长度,最后根据菱形的面积等于两对角线乘积的一半即可求出菱形的面积.
20.【答案】或;8;不能
21.【答案】(1)解: 如图1中,
∵AF⊥BC,
∴∠AFB=∠CFE=90°,
∵∠EBC=45°,
∴∠EBF=∠BEF=45°,
∴FB=FE,
∵∠BAF=∠ECF,
∴△AFB≌△CFE(AAS),
∴AF=CF
∵AB= ,
∴AF=CF= =2,
∴BC=BF+CF=3,
∵四边形ABCD是平行四边形,
∴AD=BC=3
(2)证明:如图2中,设PG交BE于T,BE交GH于Q.
∵四边形ABCD是平行四边形,
∴AB∥CD,
∵AF⊥CD,
∴AF⊥AB,
∴∠BAE=∠EFC=90°,
∵∠BEC=90°,
∴∠AEB+∠CEF=90°,∠CEF+∠ECF=90°,
∴∠AEB=∠ECF,
∵AE=CF,
∴△BAE≌△EFC(ASA),
∴BE=EC,
∵GP=EC,
∴GP=BE,
∵GP⊥BE,
∴∠GTQ=90°,
∵BH=GH,∠BHG=90°,
∴∠BHQ=∠GTQ,
∵∠GQT=∠BQH,
∴∠HGP=∠HBE,
∴△EHB≌△PHG(SAS),
∴EH=PH,∠TEO=∠OPH,
∵∠EOT=∠POH,
∴∠PHO=∠ETO=90°,
∴△EHP是等腰直角三角形,
∴PE= EH.
故答案为:(1)AD=3.(2)见解析.
【解析】【分析】(1)首先判断出△BEF是等腰直角三角形,根据等腰直角三角形的性质得出 ∠EBF=∠BEF=45°, FB=FE=1 ,根据勾股定理算出AF的长,然后利用AAS判断出 △AFB≌△CFE ,根据全等三角形的对应边相等得出AF=CF=2,根据线段的和差得出BC的长,根据平行四边形的对边相等得出AD的长;
(2) 如图2中,设PG交BE于T,BE交GH于Q,根据同角的余角相等得出 ∠AEB=∠ECF, 然后利用ASA判断出△BAE≌△EFC ,根据全等三角形的对应边相等得出 BE=EC, 又 GP=EC, 故 GP=BE;然后利用SAS判断出 △EHB≌△PHG ,根据全等三角形的性质得出 EH=PH,∠TEO=∠OPH, 再判断出 △EHP是等腰直角三角形, 根据等腰直角三角形的性质即可得出 PE= EH 。
22.【答案】(1)证明:于点,,
,
.
又,即,
四边形是平行四边形,
.
(2)解:四边形是菱形.
理由:是的中点,
.
又,
四边形是平行四边形.
,
平行四边形是菱形.
(3)解:若为的中点,当时,四边形是正方形.
理由如下:,,
,
.
又是的中点,
,
即.
菱形是正方形.
【解析】【分析】(1)首先根据平行四边形的判定得出四边形是平行四边形,再根据平行四边形对边相等,即可得出结论;
(2)首先证得四边形是平行四边形,再根据对角线垂直,即可得出平行四边形是菱形;
(3)若为的中点,当时,四边形是正方形.由(2)知平行四边形是菱形,再根据等腰三角形CAB中,根据三线合一的性质得出,即可得出 四边形是正方形 .
23.【答案】(1)证明:因为 ,
所以 , ,
又因为 ,
所以四边形AFCE为平行四边形,
所以AF∥CE,
因为AD-AE=BC-CF,即DE=BF,
因为DE∥BF,
所以四边形 为平行四边形,
所以
所以四边形 为平行四边形.
(2)解:以 为边的平行四边形有 、 、 、 .
∵ ,
∴ , ,
∵ 是 的中点,
∴AE=DE= ,
∵ ,
∴CF= ,
∴点F为BC中点,
∴AE=DE=BF=CF,
∴四边形AFCE与四边形EBFD均为平行四边形
∴AF∥EC,EB∥DF,
∴∠EAM=∠DEN,∠AEM=∠EDN,
在△AME和△END中
∴△AME≌△END(ASA)
∴AM=EN,
又∵AM∥EN,
∴四边形AENM为平行四边形,
∴AE∥MN,且AE=MN,
∴ED∥MN,且ED=MN,
∴四边形EDNM为平行四边形,
∴BF∥MN,且BF=MN,
∴四边形BMNF为平行四边形,
∴FC∥MN,且FC=MN,
∴四边形FCNM为平行四边形,
∴以 为边的平行四边形有 、 、 、 .
【解析】【分析】(1)先求出 , , 再求出 DE∥BF, 最后证明求解即可;
(2)先求出 AE=DE= , 再求出 △AME≌△END ,最后证明求解即可。
24.【答案】(1)点、的坐标分别为、
(2)①或;②或或
21世纪教育网(www.21cnjy.com)
同课章节目录
