贵州省黔东南苗族侗族自治州凯里市第一中学2025届高三模拟考试数学试卷(Ⅲ)(含解析)
文档属性
| 名称 | 贵州省黔东南苗族侗族自治州凯里市第一中学2025届高三模拟考试数学试卷(Ⅲ)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-08 22:37:18 | ||
图片预览




文档简介
贵州省凯里市第一中学2025届高三模拟考试数学试卷(Ⅲ)
一、单选题
1.已知复数z满足,则( )
A. B. C. D.
2.已知集合,则( )
A. B.
C. D.
3.命题“”的否定是( )
A. B.
C. D.
4.在人工智能芯片的性能测试中,若芯片处理数据的错误率E与芯片的运算速度v(单位:)满足函数关系,则当芯片处理数据的运算速度为时,芯片处理数据的错误率约为(参考数据:)( )
A. B. C. D.
5.已知,则( )
A. B. C. D.
6.已知点P是双曲线上第一象限的点,C的左、右焦点分别为,若是面积为的等边三角形(O为坐标原点),则直线的方程是( )
A. B.
C. D.
7.某礼品盒生产厂设计了一款如图所示的八面体形礼品包装盒,该八面体是由正四面体在4个顶点处分别截去一个棱长为的小正四面体而得到的.已知该礼品包装盒的高度为,若不考虑包装盒材料的厚度,则该礼品包装盒的体积为( )
A. B.
C. D.
8.如图,在梯形中,,P是外接圆上的动点,则的最大值为( )
A. B. C. D.
9.2025年热播的国产动画电影《哪吒2之魔童闹海》自1月29日在国内首映以来连破票房记录,于3月15日进入全球电影票房榜第五位.它不仅在技术上实现了中国动画电影的突破,更在主题上蕴含了丰富的社会寓意.影片通过对经典神话故事的重新解读,探讨了命运、偏见与人性的复杂议题,同时也反映了中国当代社会的价值观念和文化自信,推动了中国传统文化的传承与创新.现摘取2月4日至2月7日的统计数据如下:
日期 2月4日 2月5日 2月6日 2月7日
首映日起第x天 7 8 9 10
单日观影人次y(亿人次)
单日综合票房z(亿元)
则下列说法正确的是( )
A.从表中数据看,累计综合票房增长放缓
B.x与y负相关
C.y与z负相关
D.经计算,这四天中y与z的经验回归方程为,则
二、多选题
10.在锐角中,角所对的边分别为,已知的角平分线交于点D,,则( )
A.
B.若,则
C.面积的最大值为
D.若,则
11.如图,已知圆锥的顶点为P,底面圆为O,A,B为底面圆周上的点,,M是底面圆周上异于A,B的动点,已知圆锥的母线长为,侧面积为,则( )
A.的面积为
B.若以O为球心的球与平面相切,则球的半径为
C.存在点M,使得
D.存在点M,使得平面平面
三、填空题
12.从0,2 中选一个数字,从1,3,5中选两个数字,组成无重复数字的三位数,其中奇数的个数为 .
13.直线与圆交于两点,若的最大值为4,则的最小值为 .
14.已知函数,若对任意且,不等式恒成立,则实数a的最大值为 .
四、解答题
15.已知等差数列的前n项和为,等比数列的首项为2,且,.
(1)求的通项公式;
(2)设,求数列的前项的和.
16.设函数.
(1)若,试求函数的极值;
(2)设,讨论的单调性.
17.春节是中华民族的传统节日,每逢春节来临前,各地均举行丰富多彩的“赶年货大集”活动.某商户为了促销,在活动最后几天决定对所有未售出商品“八折”销售,对购买者在付款前还增设了先抽奖后付款奖励.商户在抽奖箱中放入质地完全相同的个红球和个黄球(),规则规定:购买者从箱中1次抽出2个小球,若抽中1个红球和1个黄球,则给予“折上折”付款奖励,即再打一次“八折”,否则按原定“八折”付款.每位购买者只抽一次,抽后小球要放回,下一位购买者再抽.
(1)当时,若3位购买者中有X位获得“折上折”付款奖励,求X的分布列与数学期望;
(2)某购买者在抽奖前对商户说:“你先抽出1个小球后我再按上述规则抽取,如何?”.请你帮商户分析是否同意购买者的要求,说明你的理由.
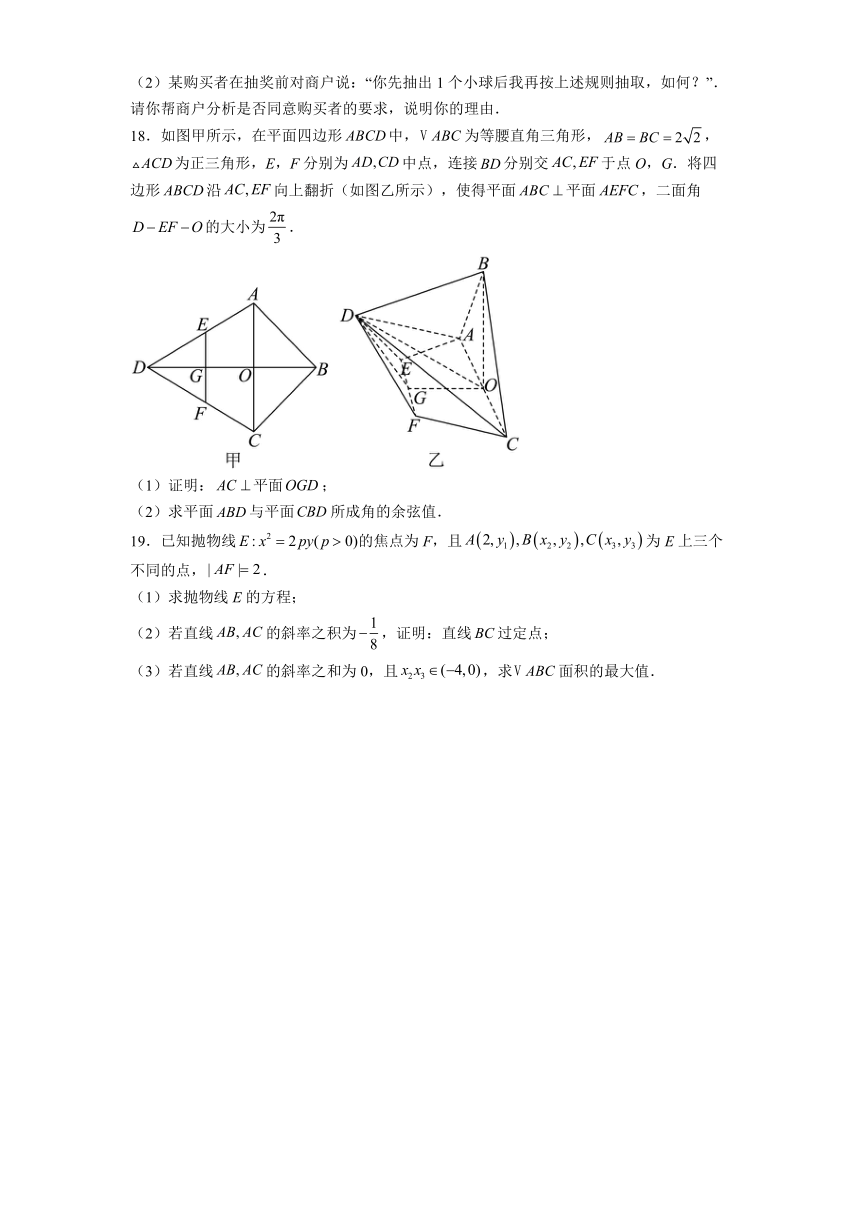
18.如图甲所示,在平面四边形中,为等腰直角三角形,,为正三角形,E,F分别为中点,连接分别交于点O,G.将四边形沿向上翻折(如图乙所示),使得平面平面,二面角的大小为.
(1)证明:平面;
(2)求平面与平面所成角的余弦值.
19.已知抛物线的焦点为F,且为E上三个不同的点,.
(1)求抛物线E的方程;
(2)若直线的斜率之积为,证明:直线过定点;
(3)若直线的斜率之和为0,且,求面积的最大值.
参考答案
1.【答案】A
【详解】已知,则.
故选:A.
2.【答案】C
【详解】由可得,所以,
则.
故选C.
3.【答案】D
【详解】由全称量词命题的否定可知,
命题的否定是,
故选D
4.【答案】B
【详解】当,
则
.
故选B
5.【答案】C
【详解】因为,可得,
化简可得,
同理可得,
两式相加得,
计算得.
故选C.
6.【答案】B
【详解】
设焦点,
,解得,
可知,在中,根据勾股定理,
所以,,可得直线方程为,化简得.
故选B.
7.【答案】D
【详解】
如图,将八面体补全为正四面体,设棱长为,底面中心为,
则,,
因为截下的小正四面体棱长为,所以小正四面体的高为,
所以正四面体的高为,即,故,
所以正四面体的体积为,
小正四面体的体积为,
所以包装盒的体积为.
故选D.
8.【答案】B
【详解】如图所示,过做,过做,
根据已知条件可知,设,
在和中列出勾股定理方程,解出,
可得,则,
如图,作外接圆,圆心为,设,
在和中,可得方程,解得,
可知圆心就在上,为EF的中点
连接,可知,所以,
据题意可知,,
,
当,即同向时,最大值为.
故选B.
9.【答案】ABD
【详解】根据表格数据A,B正确,C错误.
,
.
代入回归方程得,解得.
故选择:ABD.
10.【答案】BCD
【详解】已知,则且,所以,
所以由正弦定理得,所以且,所以,A选项错误;
若,则,则,B选项正确;
由余弦定理得,即,所以,
,当且仅当时等号成立,
所以面积的最大值为,C选项正确;
若,由余弦定理得,所以,
又因为的角平分线交于点D,所以,所以,
所以,
则,D选项正确.
故选BCD.
11.【答案】ACD
【详解】,∵,
∴为等边三角形,∴,又,
所以,故A正确;
以O为球心的球与平面相切,则球的半径即是点O到平面的距离,
,
故B错误;
在圆锥中两母线所成角最大,,
此时为钝角,故存在点M,使得,即C正确;
对于D,如图,取的中点为,连接,过作,垂足为,
因为平面,平面,故,
而平面,故平面,
而平面,故,而平面,
故平面,而平面,故,
故为二面角的平面角,
而,故,
故,故由对称性可得存在点M,使得平面平面,故D正确.
故选ACD.
12.【答案】18
【详解】试题分析:分类讨论:从0、2中选一个数字0,则0只能排在十位;从0、2中选一个数字2,则2排在十位或百位,由此可得结论.解:从0、2中选一个数字0,则0只能排在十位,从1、3、5中选两个数字排在个位与百位,共有 =6种;从0、2中选一个数字2,则2排在十位,从1、3、5中选两个数字排在个位与百位,共有=6种; 2排在百位,从1、3、5中选两个数字排在个位与十位,共有=6种;故共有3=18种,故答案为18.
考点:计数原理
点评:本题考查计数原理的运用,考查分类讨论的数学思想,正确分类是关键
13.【答案】
【详解】因为直线与圆交于两点,
所以当的值最大时,其为圆的直径,而的最大值为4,得到,
则圆的方程为,设圆心到直线的距离为,
如图,记圆心,直线必过定点,
由圆的性质得,当时,最大,此时的值最小,
由斜率公式得,此时,
由题意得,则,
由点到直线的距离公式得,
由勾股定理得,解得,
综上可得的最小值为.
14.【答案】
【详解】不妨令,依题意,,
,令,
则,,函数在上单调递增,
因此,恒成立,
令函数,求导得,当时,;
当时,,函数在上单调递减,在上单调递增,
,因此,
所以实数a的最大值为.
15.【答案】(1),
(2)
【详解】(1)设等差数列公差为,根据题意得,解得
所以,
可知,
设等比数列的公比为,带入得,解得,
可知.
(2)有第一问可知,,则.
分组得
计算,
计算
则.
16.【答案】(1)的极大值为,无极小值
(2)当时,的单调减区间为,无增区间;
当时,的单调增区间为,单调减区间为
【详解】(1)当时,,函数的定义域为,
所以,令有,
由有,有,
所以在上单调递增,在上单调递减,
所以的极大值为,无极小值;
(2)由,
所以的定义域为,
所以,令,
当时,,,所以在单调递减;
当时,令有,,
所以,
所以由有,,有,,
所以在单调递增,在单调递减,
所以的单调增区间为,单调减区间为;
综上有:当时,的单调减区间为,无增区间;
当时,的单调增区间为,单调减区间为.
17.【答案】(1)分布列见解析;
(2)可以同意购买者的要求;理由见解析
【详解】(1)由题意得当时,共有个球,
从个球里抽取个,共有种情况,
抽取1个红球和1个黄球则有种等可能情况,
则1次抽奖获得“折上折”付款奖励的概率为,
若3位购买者中有位获得“折上折”付款奖励,则,
由二项分布概率公式得,
,,
,
则的分布列为
由二项分布的期望公式得.
(2)首先,我们设按照原规则获得“折上折”付款奖励的概率为,
按照新规则获得“折上折”付款奖励的概率为,
按照原规则,,
按照新规则,若先抽出个红球,则获得“折上折”付款奖励的概率如下,
为,
若先抽出个黄球,则获得“折上折”付款奖励的概率如下,
为,
由古典概型概率公式得抽出个红球的概率为,
同理可得抽出个黄球的概率为,
结合全概率公式可得,
,
,
得到,故商户可以同意购买者的要求.
18.【答案】(1)证明见解析
(2)
【详解】(1)证明:在平面四边形中,因为为正三角形,所以,
因为, ,
所以≌,所以,
因为,所以,为的中点,
因为E,F分别为中点,所以∥,
所以,
所以将四边形沿向上翻折后,,
因为∥,所以,
因为,平面,
所以平面;
(2)因为在平面四边形中,为等腰直角三角形,,
所以,
因为为正三角形,为的中点,
所以,,
因为为的中位线,,
所以,
由(1)知,所以为二面角的平面角,
所以,
因为平面平面,平面平面,,平面,
所以平面,
因为平面,所以,
所以两两垂直,
所以以为原点,所在的直线分别为轴建立空间直角坐标系,如图所示,
则,
因为,所以,
因为,所以,
所以,
设平面的法向量为,则
,令,可得,
则为平面的一个法向量,
设平面的法向量为,则
,令,则,
则为平面的一个法向量,
设平面与平面所成角为,则
,
所以平面与平面所成角的余弦值为.
19.【答案】(1)
(2)证明见解析
(3)
【详解】(1)由,可得,
由焦半径公式,,
解得:,
所以抛物线E的方程.
(2)由(1)知
由题意可知直线的斜率存在,设直线的方程为,
由,得:,
,,,
,
所以,
所以直线的方程为,
当时,,故恒过.
(3),
得,,
由(2)知:,
所以斜率为,
如图:
由(2),得:,
得,又,
所以,所以
所以.
又点到直线的距离为:.
所以,().
设,则,所以,().
设,()
则,
由,
由,或,
因为,所以函数在上单调递增.在单调递减,
所以.
所以.
即面积的最大值为.
一、单选题
1.已知复数z满足,则( )
A. B. C. D.
2.已知集合,则( )
A. B.
C. D.
3.命题“”的否定是( )
A. B.
C. D.
4.在人工智能芯片的性能测试中,若芯片处理数据的错误率E与芯片的运算速度v(单位:)满足函数关系,则当芯片处理数据的运算速度为时,芯片处理数据的错误率约为(参考数据:)( )
A. B. C. D.
5.已知,则( )
A. B. C. D.
6.已知点P是双曲线上第一象限的点,C的左、右焦点分别为,若是面积为的等边三角形(O为坐标原点),则直线的方程是( )
A. B.
C. D.
7.某礼品盒生产厂设计了一款如图所示的八面体形礼品包装盒,该八面体是由正四面体在4个顶点处分别截去一个棱长为的小正四面体而得到的.已知该礼品包装盒的高度为,若不考虑包装盒材料的厚度,则该礼品包装盒的体积为( )
A. B.
C. D.
8.如图,在梯形中,,P是外接圆上的动点,则的最大值为( )
A. B. C. D.
9.2025年热播的国产动画电影《哪吒2之魔童闹海》自1月29日在国内首映以来连破票房记录,于3月15日进入全球电影票房榜第五位.它不仅在技术上实现了中国动画电影的突破,更在主题上蕴含了丰富的社会寓意.影片通过对经典神话故事的重新解读,探讨了命运、偏见与人性的复杂议题,同时也反映了中国当代社会的价值观念和文化自信,推动了中国传统文化的传承与创新.现摘取2月4日至2月7日的统计数据如下:
日期 2月4日 2月5日 2月6日 2月7日
首映日起第x天 7 8 9 10
单日观影人次y(亿人次)
单日综合票房z(亿元)
则下列说法正确的是( )
A.从表中数据看,累计综合票房增长放缓
B.x与y负相关
C.y与z负相关
D.经计算,这四天中y与z的经验回归方程为,则
二、多选题
10.在锐角中,角所对的边分别为,已知的角平分线交于点D,,则( )
A.
B.若,则
C.面积的最大值为
D.若,则
11.如图,已知圆锥的顶点为P,底面圆为O,A,B为底面圆周上的点,,M是底面圆周上异于A,B的动点,已知圆锥的母线长为,侧面积为,则( )
A.的面积为
B.若以O为球心的球与平面相切,则球的半径为
C.存在点M,使得
D.存在点M,使得平面平面
三、填空题
12.从0,2 中选一个数字,从1,3,5中选两个数字,组成无重复数字的三位数,其中奇数的个数为 .
13.直线与圆交于两点,若的最大值为4,则的最小值为 .
14.已知函数,若对任意且,不等式恒成立,则实数a的最大值为 .
四、解答题
15.已知等差数列的前n项和为,等比数列的首项为2,且,.
(1)求的通项公式;
(2)设,求数列的前项的和.
16.设函数.
(1)若,试求函数的极值;
(2)设,讨论的单调性.
17.春节是中华民族的传统节日,每逢春节来临前,各地均举行丰富多彩的“赶年货大集”活动.某商户为了促销,在活动最后几天决定对所有未售出商品“八折”销售,对购买者在付款前还增设了先抽奖后付款奖励.商户在抽奖箱中放入质地完全相同的个红球和个黄球(),规则规定:购买者从箱中1次抽出2个小球,若抽中1个红球和1个黄球,则给予“折上折”付款奖励,即再打一次“八折”,否则按原定“八折”付款.每位购买者只抽一次,抽后小球要放回,下一位购买者再抽.
(1)当时,若3位购买者中有X位获得“折上折”付款奖励,求X的分布列与数学期望;
(2)某购买者在抽奖前对商户说:“你先抽出1个小球后我再按上述规则抽取,如何?”.请你帮商户分析是否同意购买者的要求,说明你的理由.
18.如图甲所示,在平面四边形中,为等腰直角三角形,,为正三角形,E,F分别为中点,连接分别交于点O,G.将四边形沿向上翻折(如图乙所示),使得平面平面,二面角的大小为.
(1)证明:平面;
(2)求平面与平面所成角的余弦值.
19.已知抛物线的焦点为F,且为E上三个不同的点,.
(1)求抛物线E的方程;
(2)若直线的斜率之积为,证明:直线过定点;
(3)若直线的斜率之和为0,且,求面积的最大值.
参考答案
1.【答案】A
【详解】已知,则.
故选:A.
2.【答案】C
【详解】由可得,所以,
则.
故选C.
3.【答案】D
【详解】由全称量词命题的否定可知,
命题的否定是,
故选D
4.【答案】B
【详解】当,
则
.
故选B
5.【答案】C
【详解】因为,可得,
化简可得,
同理可得,
两式相加得,
计算得.
故选C.
6.【答案】B
【详解】
设焦点,
,解得,
可知,在中,根据勾股定理,
所以,,可得直线方程为,化简得.
故选B.
7.【答案】D
【详解】
如图,将八面体补全为正四面体,设棱长为,底面中心为,
则,,
因为截下的小正四面体棱长为,所以小正四面体的高为,
所以正四面体的高为,即,故,
所以正四面体的体积为,
小正四面体的体积为,
所以包装盒的体积为.
故选D.
8.【答案】B
【详解】如图所示,过做,过做,
根据已知条件可知,设,
在和中列出勾股定理方程,解出,
可得,则,
如图,作外接圆,圆心为,设,
在和中,可得方程,解得,
可知圆心就在上,为EF的中点
连接,可知,所以,
据题意可知,,
,
当,即同向时,最大值为.
故选B.
9.【答案】ABD
【详解】根据表格数据A,B正确,C错误.
,
.
代入回归方程得,解得.
故选择:ABD.
10.【答案】BCD
【详解】已知,则且,所以,
所以由正弦定理得,所以且,所以,A选项错误;
若,则,则,B选项正确;
由余弦定理得,即,所以,
,当且仅当时等号成立,
所以面积的最大值为,C选项正确;
若,由余弦定理得,所以,
又因为的角平分线交于点D,所以,所以,
所以,
则,D选项正确.
故选BCD.
11.【答案】ACD
【详解】,∵,
∴为等边三角形,∴,又,
所以,故A正确;
以O为球心的球与平面相切,则球的半径即是点O到平面的距离,
,
故B错误;
在圆锥中两母线所成角最大,,
此时为钝角,故存在点M,使得,即C正确;
对于D,如图,取的中点为,连接,过作,垂足为,
因为平面,平面,故,
而平面,故平面,
而平面,故,而平面,
故平面,而平面,故,
故为二面角的平面角,
而,故,
故,故由对称性可得存在点M,使得平面平面,故D正确.
故选ACD.
12.【答案】18
【详解】试题分析:分类讨论:从0、2中选一个数字0,则0只能排在十位;从0、2中选一个数字2,则2排在十位或百位,由此可得结论.解:从0、2中选一个数字0,则0只能排在十位,从1、3、5中选两个数字排在个位与百位,共有 =6种;从0、2中选一个数字2,则2排在十位,从1、3、5中选两个数字排在个位与百位,共有=6种; 2排在百位,从1、3、5中选两个数字排在个位与十位,共有=6种;故共有3=18种,故答案为18.
考点:计数原理
点评:本题考查计数原理的运用,考查分类讨论的数学思想,正确分类是关键
13.【答案】
【详解】因为直线与圆交于两点,
所以当的值最大时,其为圆的直径,而的最大值为4,得到,
则圆的方程为,设圆心到直线的距离为,
如图,记圆心,直线必过定点,
由圆的性质得,当时,最大,此时的值最小,
由斜率公式得,此时,
由题意得,则,
由点到直线的距离公式得,
由勾股定理得,解得,
综上可得的最小值为.
14.【答案】
【详解】不妨令,依题意,,
,令,
则,,函数在上单调递增,
因此,恒成立,
令函数,求导得,当时,;
当时,,函数在上单调递减,在上单调递增,
,因此,
所以实数a的最大值为.
15.【答案】(1),
(2)
【详解】(1)设等差数列公差为,根据题意得,解得
所以,
可知,
设等比数列的公比为,带入得,解得,
可知.
(2)有第一问可知,,则.
分组得
计算,
计算
则.
16.【答案】(1)的极大值为,无极小值
(2)当时,的单调减区间为,无增区间;
当时,的单调增区间为,单调减区间为
【详解】(1)当时,,函数的定义域为,
所以,令有,
由有,有,
所以在上单调递增,在上单调递减,
所以的极大值为,无极小值;
(2)由,
所以的定义域为,
所以,令,
当时,,,所以在单调递减;
当时,令有,,
所以,
所以由有,,有,,
所以在单调递增,在单调递减,
所以的单调增区间为,单调减区间为;
综上有:当时,的单调减区间为,无增区间;
当时,的单调增区间为,单调减区间为.
17.【答案】(1)分布列见解析;
(2)可以同意购买者的要求;理由见解析
【详解】(1)由题意得当时,共有个球,
从个球里抽取个,共有种情况,
抽取1个红球和1个黄球则有种等可能情况,
则1次抽奖获得“折上折”付款奖励的概率为,
若3位购买者中有位获得“折上折”付款奖励,则,
由二项分布概率公式得,
,,
,
则的分布列为
由二项分布的期望公式得.
(2)首先,我们设按照原规则获得“折上折”付款奖励的概率为,
按照新规则获得“折上折”付款奖励的概率为,
按照原规则,,
按照新规则,若先抽出个红球,则获得“折上折”付款奖励的概率如下,
为,
若先抽出个黄球,则获得“折上折”付款奖励的概率如下,
为,
由古典概型概率公式得抽出个红球的概率为,
同理可得抽出个黄球的概率为,
结合全概率公式可得,
,
,
得到,故商户可以同意购买者的要求.
18.【答案】(1)证明见解析
(2)
【详解】(1)证明:在平面四边形中,因为为正三角形,所以,
因为, ,
所以≌,所以,
因为,所以,为的中点,
因为E,F分别为中点,所以∥,
所以,
所以将四边形沿向上翻折后,,
因为∥,所以,
因为,平面,
所以平面;
(2)因为在平面四边形中,为等腰直角三角形,,
所以,
因为为正三角形,为的中点,
所以,,
因为为的中位线,,
所以,
由(1)知,所以为二面角的平面角,
所以,
因为平面平面,平面平面,,平面,
所以平面,
因为平面,所以,
所以两两垂直,
所以以为原点,所在的直线分别为轴建立空间直角坐标系,如图所示,
则,
因为,所以,
因为,所以,
所以,
设平面的法向量为,则
,令,可得,
则为平面的一个法向量,
设平面的法向量为,则
,令,则,
则为平面的一个法向量,
设平面与平面所成角为,则
,
所以平面与平面所成角的余弦值为.
19.【答案】(1)
(2)证明见解析
(3)
【详解】(1)由,可得,
由焦半径公式,,
解得:,
所以抛物线E的方程.
(2)由(1)知
由题意可知直线的斜率存在,设直线的方程为,
由,得:,
,,,
,
所以,
所以直线的方程为,
当时,,故恒过.
(3),
得,,
由(2)知:,
所以斜率为,
如图:
由(2),得:,
得,又,
所以,所以
所以.
又点到直线的距离为:.
所以,().
设,则,所以,().
设,()
则,
由,
由,或,
因为,所以函数在上单调递增.在单调递减,
所以.
所以.
即面积的最大值为.
同课章节目录
