13.1.2三角形中角的关系(1)课件(共26张PPT)
文档属性
| 名称 | 13.1.2三角形中角的关系(1)课件(共26张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-07 19:42:56 | ||
图片预览








文档简介
(共26张PPT)
逐点
导讲练
课堂小结
作业提升
课时讲解
1
课时流程
2
三角形按角分类
三角形的内角和定理
知1-讲
知识点
三角形按角分类
1
1. 各类三角形的概念
(1)锐角三角形:三角形中 , 三个角都是锐角的三角形叫做锐角三角形 .
(2)直角三角形:三角形中 , 有一个角是直角的三角形叫做直角三角形 .
(3)钝角三角形:三角形中,有一个角是钝角的三角形叫做钝角三角形 .
知1-讲
拓展
1. 三角形的内角中,最多有一个直角或一个钝角;最少有两个锐角 .
2. 三角形按边分类和按角分类是两种不同的分类方式,各自独立,无论按哪种标准分类 , 原则都是不重不漏 .
3. 同一个三角形可能同时属于两种不同的分类 ,如等腰直角三角形,按边分类属于等腰三角形,按角分类属于直角三角形 .
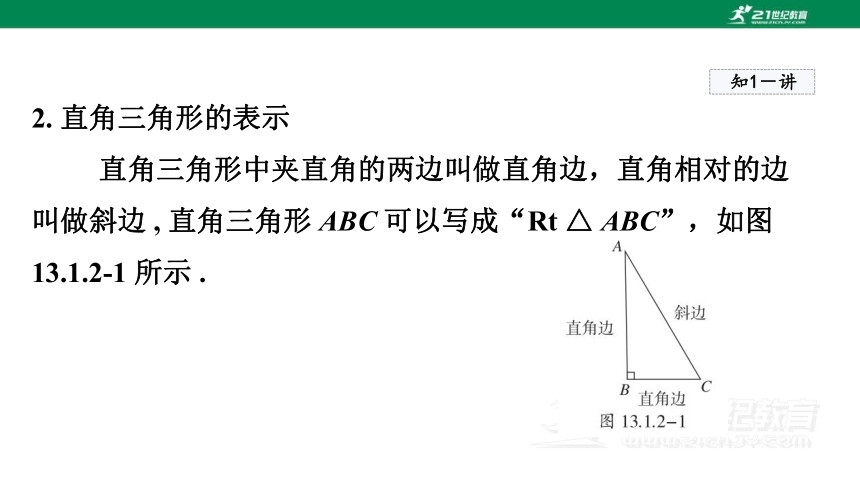
2. 直角三角形的表示
直角三角形中夹直角的两边叫做直角边,直角相对的边
叫做斜边 , 直角三角形 ABC 可以写成“Rt △ ABC”,如图
13.1.2-1 所示 .
知1-讲
知1-讲
知1-练
下列说法中,正确的有( )
①锐角三角形中最大的角一定小于 90°;②所有的等边三角形都是锐角三角形;③所有的等腰三角形都是锐角三角形;④直角三角形一定不是等腰三角形 .
A. 1 个 B. 2 个
C. 3 个 D. 4 个
例1
知1-练
解题秘方:紧扣三角形分类的标准进行辨析 .
①锐角三角形的三个角都为锐角,锐角小于 90°,故正确;
②等边三角形的三个角都为 60°,所以它是锐角三角形,故正确;
③对于顶角是钝角的等腰三角形,不满足结论,故错误;
知1-练
方法点拨
此题考查三角形的分类,按角分类的关键是先观察一个三角形中是否有直角或钝角;按边分类应观察一个三角形中是否有相等的边,有几条相等的边 .
知1-练
④直角三角形可能是等腰三角形,三角尺中就有一个是等腰的直角三角形,故错误 . 故选 B.
答案:B
知2-讲
知识点
三角形的内角和定理
2
1.定理
三角形三个内角的和等于 180° .
几何语言: 在△ ABC 中,∠ A+ ∠ B+ ∠ C=180° .
知2-讲
特别解读
1.三角形内角和定理揭示了三角形三个内角之间的数量关系 .
2.三角形的三个内角中最多只有一个钝角或直角,或者说至少有两个锐角 .
2. 说明三角形的内角和定理的思路
思路一:利用“两直线平行,内错角及同位角相等”将三角形的三个内角转化为一个平角 . 如图 13.1.2-2 ①② .
知2-讲
知2-讲
特别提醒
说明三角形的内角和定理的思路方法:
主要是运用平行线作为桥梁,将三个内角“转移”集中成一个角或两个角,再说明这个角或两个角的和是 180°即可 .
思路二:利用“两直线平行,内错角相等”将三角形的三个内角转化为两平行线间的一组同旁内角 . 如图 13.1.2-3 ①② .
知2-讲
知2-练
∠ A,∠ B,∠ C 是△ ABC 的三个内角 .
解题秘方:紧扣三角形的内角和定理建立方程(组)求解 .
例2
知2-练
(1)已知∠ A=40°,∠ B= ∠ C,求∠ B,∠ C 的度数;
解:设∠ B= ∠ C=x°,
因为∠ A+ ∠ B+ ∠ C=180°,∠ A=40°,
所以40+x+x=180,
解得 x=70,所以∠ B= ∠ C=70° .
知2-练
另解
因为 ∠ A+ ∠ B+∠ C=180°,∠ A=40°,
所以∠B+∠C=180° - 40° =140° .
又因为∠B=∠C,所以∠B= ∠C=140° ÷2=70° .
知2-练
(2)已知∠ A-∠ B=16°,∠ C=54°,求∠ A,∠ B 的度数;
知2-练
知2-练
知2-练
教你一招:三角形中求角的度数问题一般用方程思想求解 . 当角之间存在某种数量关系时,一般根据三角形的内角和为 180°列方程求解 .
知2-练
方法点拨
求三角形内角的度数的方法:
1. 若已知两个角的度数,求第三个角的度数,直接利用三角形的内角和求解 .
2. 若已知一 个角的 度数及另两个角之间的数量关系;或不知道任何一个角的度数,只知道三个角之间的数量关系,一般根据 “三角形的内角和为180 ° ” 这 个 隐 含 的数量关系列方程(或方程组)求解 .
知2-练
一个零件的形状如图 13.1.2-4 所示,按规定∠ A 应等于 90°,∠ ABD,∠ ACD 应分别是 34°和 18° . 李叔叔量得∠ BDC=146°,请你帮李叔叔判断这个零件是否合格,并说明理由 .
例3
知2-练
解题秘方:建立三角形的模型利用三角形内角和求出角度和,再用三角形内角和进行验证 .
解法提醒
“三角形的内角和等于 180°”这个定理是任何三角形都必须具备的性质 .
知2-练
解:这个零件不合格,理由:如图 13.1.2-4,连接 BC,
在△ ABC 中, ∠ A+ ∠ ABC+ ∠ ACB=180°,
因为∠ A=90°,∠ ACD=18°,∠ ABD=34°,
所以∠ DCB+ ∠ DBC=38°.
在△ DCB 中,∠ BDC=180°- (∠ DCB+
∠ DBC)=180°- 38°=142°≠ 146°,
所以这个零件不合格 .
三角形中角的关系
内角和等
于 180°
三个内角的
数量关系
三 角
形 中
角 的
关系
直角三角形
斜三角形
最大角
的大小
逐点
导讲练
课堂小结
作业提升
课时讲解
1
课时流程
2
三角形按角分类
三角形的内角和定理
知1-讲
知识点
三角形按角分类
1
1. 各类三角形的概念
(1)锐角三角形:三角形中 , 三个角都是锐角的三角形叫做锐角三角形 .
(2)直角三角形:三角形中 , 有一个角是直角的三角形叫做直角三角形 .
(3)钝角三角形:三角形中,有一个角是钝角的三角形叫做钝角三角形 .
知1-讲
拓展
1. 三角形的内角中,最多有一个直角或一个钝角;最少有两个锐角 .
2. 三角形按边分类和按角分类是两种不同的分类方式,各自独立,无论按哪种标准分类 , 原则都是不重不漏 .
3. 同一个三角形可能同时属于两种不同的分类 ,如等腰直角三角形,按边分类属于等腰三角形,按角分类属于直角三角形 .
2. 直角三角形的表示
直角三角形中夹直角的两边叫做直角边,直角相对的边
叫做斜边 , 直角三角形 ABC 可以写成“Rt △ ABC”,如图
13.1.2-1 所示 .
知1-讲
知1-讲
知1-练
下列说法中,正确的有( )
①锐角三角形中最大的角一定小于 90°;②所有的等边三角形都是锐角三角形;③所有的等腰三角形都是锐角三角形;④直角三角形一定不是等腰三角形 .
A. 1 个 B. 2 个
C. 3 个 D. 4 个
例1
知1-练
解题秘方:紧扣三角形分类的标准进行辨析 .
①锐角三角形的三个角都为锐角,锐角小于 90°,故正确;
②等边三角形的三个角都为 60°,所以它是锐角三角形,故正确;
③对于顶角是钝角的等腰三角形,不满足结论,故错误;
知1-练
方法点拨
此题考查三角形的分类,按角分类的关键是先观察一个三角形中是否有直角或钝角;按边分类应观察一个三角形中是否有相等的边,有几条相等的边 .
知1-练
④直角三角形可能是等腰三角形,三角尺中就有一个是等腰的直角三角形,故错误 . 故选 B.
答案:B
知2-讲
知识点
三角形的内角和定理
2
1.定理
三角形三个内角的和等于 180° .
几何语言: 在△ ABC 中,∠ A+ ∠ B+ ∠ C=180° .
知2-讲
特别解读
1.三角形内角和定理揭示了三角形三个内角之间的数量关系 .
2.三角形的三个内角中最多只有一个钝角或直角,或者说至少有两个锐角 .
2. 说明三角形的内角和定理的思路
思路一:利用“两直线平行,内错角及同位角相等”将三角形的三个内角转化为一个平角 . 如图 13.1.2-2 ①② .
知2-讲
知2-讲
特别提醒
说明三角形的内角和定理的思路方法:
主要是运用平行线作为桥梁,将三个内角“转移”集中成一个角或两个角,再说明这个角或两个角的和是 180°即可 .
思路二:利用“两直线平行,内错角相等”将三角形的三个内角转化为两平行线间的一组同旁内角 . 如图 13.1.2-3 ①② .
知2-讲
知2-练
∠ A,∠ B,∠ C 是△ ABC 的三个内角 .
解题秘方:紧扣三角形的内角和定理建立方程(组)求解 .
例2
知2-练
(1)已知∠ A=40°,∠ B= ∠ C,求∠ B,∠ C 的度数;
解:设∠ B= ∠ C=x°,
因为∠ A+ ∠ B+ ∠ C=180°,∠ A=40°,
所以40+x+x=180,
解得 x=70,所以∠ B= ∠ C=70° .
知2-练
另解
因为 ∠ A+ ∠ B+∠ C=180°,∠ A=40°,
所以∠B+∠C=180° - 40° =140° .
又因为∠B=∠C,所以∠B= ∠C=140° ÷2=70° .
知2-练
(2)已知∠ A-∠ B=16°,∠ C=54°,求∠ A,∠ B 的度数;
知2-练
知2-练
知2-练
教你一招:三角形中求角的度数问题一般用方程思想求解 . 当角之间存在某种数量关系时,一般根据三角形的内角和为 180°列方程求解 .
知2-练
方法点拨
求三角形内角的度数的方法:
1. 若已知两个角的度数,求第三个角的度数,直接利用三角形的内角和求解 .
2. 若已知一 个角的 度数及另两个角之间的数量关系;或不知道任何一个角的度数,只知道三个角之间的数量关系,一般根据 “三角形的内角和为180 ° ” 这 个 隐 含 的数量关系列方程(或方程组)求解 .
知2-练
一个零件的形状如图 13.1.2-4 所示,按规定∠ A 应等于 90°,∠ ABD,∠ ACD 应分别是 34°和 18° . 李叔叔量得∠ BDC=146°,请你帮李叔叔判断这个零件是否合格,并说明理由 .
例3
知2-练
解题秘方:建立三角形的模型利用三角形内角和求出角度和,再用三角形内角和进行验证 .
解法提醒
“三角形的内角和等于 180°”这个定理是任何三角形都必须具备的性质 .
知2-练
解:这个零件不合格,理由:如图 13.1.2-4,连接 BC,
在△ ABC 中, ∠ A+ ∠ ABC+ ∠ ACB=180°,
因为∠ A=90°,∠ ACD=18°,∠ ABD=34°,
所以∠ DCB+ ∠ DBC=38°.
在△ DCB 中,∠ BDC=180°- (∠ DCB+
∠ DBC)=180°- 38°=142°≠ 146°,
所以这个零件不合格 .
三角形中角的关系
内角和等
于 180°
三个内角的
数量关系
三 角
形 中
角 的
关系
直角三角形
斜三角形
最大角
的大小
