14.1 全等三角形及其性质 课件(共33张PPT)
文档属性
| 名称 | 14.1 全等三角形及其性质 课件(共33张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-07 19:39:19 | ||
图片预览










文档简介
(共33张PPT)
逐点
导讲练
课堂小结
作业提升
课时讲解
1
课时流程
2
全等形
全等三角形
全等三角形的性质
知1-讲
知识点
全等形
1
1. 定义 能够 完全重合的两个图形,叫做全等形 .
全等形的特征: 两相同与两无关 .
(1)两相同:①形状相同;②大小相同 .
(2)两无关:①与位置无关;②与方向无关 .
知1-讲
特别解读
◆完全重合说明两个图形周长和面积相等;
◆周长或面积相等的两个图形不一定是全等的 .
2. 全等变换的常见方式 平移、翻折、旋转 .
知1-讲
知1-练
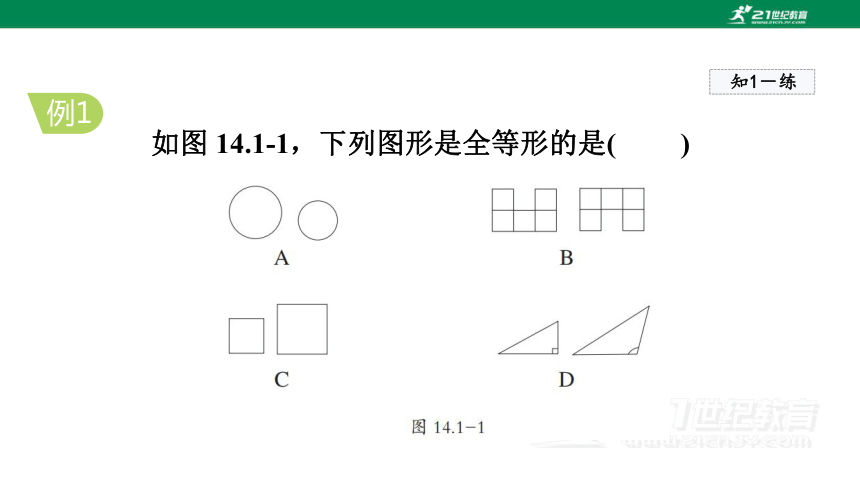
如图 14.1-1,下列图形是全等形的是( )
例1
知1-练
解:选项 A、 C 大小不同;选项 D 形状不同,故选 B.
解题秘方:根据全等形的定义和特征进行判断 .
答案:B
方法点拨
确定两个图形全等的方法:
1. 条件判定法:
(1)形状相同;(2)大小相等 .
是否是全等形与位置无关 .
2. 重合判定法: 通过平移、旋转、翻折等方法把两个图形叠合在一起,看它们能否完全重合 .
知1-练
知2-讲
知识点
全等三角形
2
1. 全等三角形的相关概念
(1) 全等三角形的概念: 能够完全重合的两个三角形叫做全等三角形 .
(2) 全等三角形的对应元素:
①对应顶点: 全等三角形中互相重合的顶点 .
②对应边: 全等三角形中互相重合的边 .
③对应角: 全等三角形中互相重合的角.
知2-讲
特别解读
对应边或对应角与对边或对角的区别:
对应边、对应角是两个全等三角形中对应的两条边之间或对应的两个角之间的关系;对边、对角是同一个三角形中边和角之间的关系, “对边”是指三角形中某个角所对的边,“对角” 是指三角形中某条边所对的角 .
知2-讲
2. 全等三角形的表示方法
全等用符号“≌”表示,读作“全等于”,记两个三角
形全等时,通常把表示对应顶点的字母写在对应的位置上 .
知2-讲
示图
如图 14.1-2 中的△ ABC 和△ DEF 全等,记作△ ABC ≌△ DEF,读 作 “ △ ABC 全等于△ DEF”,其中点 A 和点 D,点 B 和点 E,点C 和点 F 是对应顶点,AB 和 DE,BC 和 EF,AC和 DF 是对应边,∠ A和∠ D,∠ B 和∠ E,∠ C 和∠ F 是对应角.
知2-讲
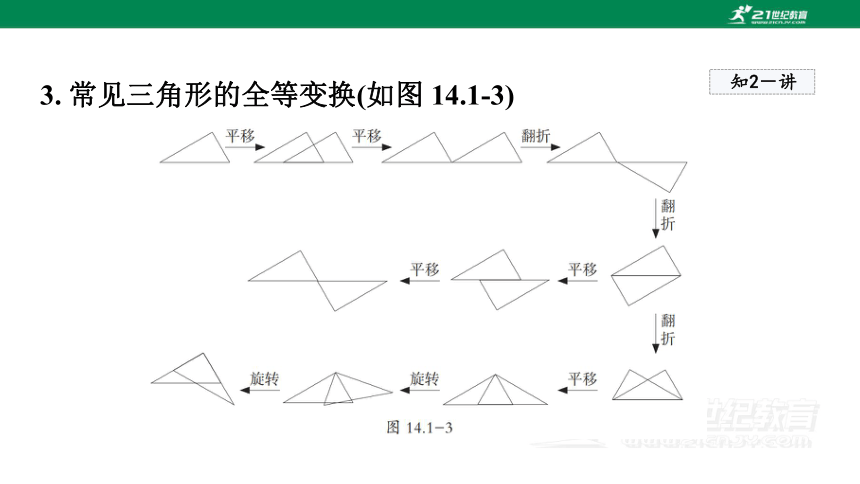
3. 常见三角形的全等变换(如图 14.1-3)
知2-讲
4. 对应元素的确定方法
(1) 图形特征法:
①最长边对最长边,最短边对最短边.
②最大角对最大角,最小角对最小角.
③相等的边(角)为对应边(角).
知2-讲
(2) 位置关系法:
①公共角(对顶角)为对应角,公共边为对应边.
②对应角的对边为对应边,两个对应角所夹的边是对应边.
③对应边的对角为对应角,两条对应边所夹的角是对应角.
(3) 字母顺序法:
根据书写规范按照对应顶点确定对应边或对应角 .
知2-讲
特别解读
对应关系可从两个方面理解 .
(1)从动态角度理解:重合是找对应元素的关键 .
(2)从静态角度理解:
从表示方法中找准对应顶点,然后确定对应边和对应角 .
知2-练
如图 14.1-4,已知△ ABD ≌△ CDB,∠ ABD= ∠ CDB. 写出其对应边和对应角 .
例2
知2-练
解题秘方:根据图形的位置特征确定对应边和对应角 .
解:BD 与 DB, AD 与 CB, AB 与 CD 是对应边;∠ A 与∠ C,∠ ABD 与∠ CDB,∠ ADB 与
∠ CBD 是对应角 .
解法提醒
利用图形的位置特征确定对应边和对应角时,要抓住对应边所对的角是对应角,对应角所对的边是对应边;当全等三角形的两组对应边(角)已确定时,剩下的一组边(角)就是对应边(角).
知2-练
知2-练
如图 14.1-5,将△ ABC 绕其顶点 B 顺时针旋转一定角度后得到△ DBE,请说出图中△ ABC 和△ DBE 是否为全等三角形,若是,写出其对应边和对应角 .
例3
知2-练
解题秘方:根据图形旋转前后的对应位置找对应元素 .
解:△ ABC ≌ △ DBE. AB 与 DB, AC 与 DE, BC 与 BE是对应边,∠ A 与∠ BDE,∠ ABC 与∠ DBE,
∠ C 与∠ E 是对应角 .
解法提醒
从动态的角度找对应元素,关键抓住图形变换前后的重合元素,重合的边为对应边,重合的角为对应角 .
知2-练
知3-讲
知识点
全等三角形的性质
3
知3-讲
2. 拓展 全等三角形的对应元素相等 .
全等三角形中的对应元素包括对应边、对应角、对应边上的中线、对应边上的高、对应角的平分线、周长、面积等 .
知3-讲
要点提醒
1. 应用全等三角形的性质时,要先确定两个条件:
(1)两个三角形全等;
(2)找对应元素 .
2. 全等三角形的性质是证明线段、角相等的常用方法.
知3-练
如图 14.1-6,已知△ ABF ≌△ CDE.
(1)若∠ B=38°,∠ DCF=42°,求∠ EFC 的度数;
(2)若 BD=10, EF=2,求 BF 的长.
例4
知3-练
解题秘方:利用全等三角形的对应边相等和对应角相等解决问题 .
解:(1) ∵△ ABF ≌△ CDE,
∴∠ D= ∠ B=38°,
∴∠ EFC= ∠ DCF+ ∠ D=42° +38° =80° .
解法提醒
全等三角形的对应边(对应角)相等,由此可得两条线段(两个角)相等,从而进一步说明线段(角)的相等关系、和差关系或求线段的长度、角的大小 .
知3-练
知3-练
证明: (2) ∵△ ABF ≌△ CDE,∴ BF=DE,
∴ BF-EF=DE-EF,即 BE=DF.
∵ BD=10, EF=2,
∴ BE=(10-2)÷2=4,
∴ BF=BE+EF=4+2=6.
知3-练
如图 14.1-7,已知 Rt △ ABC ≌ Rt △ CDE,且点 B, C,D 在同一条直线上,试判断 AC 与 CE 的位置关系,并给予证明 .
例5
方法点拨
证线段位置关系的方法:
证线段与线段的位置关系通常考虑平行、垂直两种特殊关系,证平行的方法是转化为证明同位角相等、内错角相等或同旁内角互补;证垂直的方法是转化为证明它们的夹角为90° 或三角形的两内角互余.
知3-练
知3-练
解题秘方:通过求 AC, CE 夹角的度数判断其位置关系 .
知3-练
解: AC ⊥ CE.
证明如下:∵ Rt △ ABC ≌ Rt △ CDE,
∴∠ BAC= ∠ DCE.
∵∠ BAC+ ∠ ACB=90°,∴∠ DCE+ ∠ ACB=90°.
∴∠ ACE=180°- (∠ DCE+ ∠ ACB)=180°-90°=90°.
∴ AC ⊥ CE.
全等三角形
全等形
特例
全等三角形
性质
对应元素
逐点
导讲练
课堂小结
作业提升
课时讲解
1
课时流程
2
全等形
全等三角形
全等三角形的性质
知1-讲
知识点
全等形
1
1. 定义 能够 完全重合的两个图形,叫做全等形 .
全等形的特征: 两相同与两无关 .
(1)两相同:①形状相同;②大小相同 .
(2)两无关:①与位置无关;②与方向无关 .
知1-讲
特别解读
◆完全重合说明两个图形周长和面积相等;
◆周长或面积相等的两个图形不一定是全等的 .
2. 全等变换的常见方式 平移、翻折、旋转 .
知1-讲
知1-练
如图 14.1-1,下列图形是全等形的是( )
例1
知1-练
解:选项 A、 C 大小不同;选项 D 形状不同,故选 B.
解题秘方:根据全等形的定义和特征进行判断 .
答案:B
方法点拨
确定两个图形全等的方法:
1. 条件判定法:
(1)形状相同;(2)大小相等 .
是否是全等形与位置无关 .
2. 重合判定法: 通过平移、旋转、翻折等方法把两个图形叠合在一起,看它们能否完全重合 .
知1-练
知2-讲
知识点
全等三角形
2
1. 全等三角形的相关概念
(1) 全等三角形的概念: 能够完全重合的两个三角形叫做全等三角形 .
(2) 全等三角形的对应元素:
①对应顶点: 全等三角形中互相重合的顶点 .
②对应边: 全等三角形中互相重合的边 .
③对应角: 全等三角形中互相重合的角.
知2-讲
特别解读
对应边或对应角与对边或对角的区别:
对应边、对应角是两个全等三角形中对应的两条边之间或对应的两个角之间的关系;对边、对角是同一个三角形中边和角之间的关系, “对边”是指三角形中某个角所对的边,“对角” 是指三角形中某条边所对的角 .
知2-讲
2. 全等三角形的表示方法
全等用符号“≌”表示,读作“全等于”,记两个三角
形全等时,通常把表示对应顶点的字母写在对应的位置上 .
知2-讲
示图
如图 14.1-2 中的△ ABC 和△ DEF 全等,记作△ ABC ≌△ DEF,读 作 “ △ ABC 全等于△ DEF”,其中点 A 和点 D,点 B 和点 E,点C 和点 F 是对应顶点,AB 和 DE,BC 和 EF,AC和 DF 是对应边,∠ A和∠ D,∠ B 和∠ E,∠ C 和∠ F 是对应角.
知2-讲
3. 常见三角形的全等变换(如图 14.1-3)
知2-讲
4. 对应元素的确定方法
(1) 图形特征法:
①最长边对最长边,最短边对最短边.
②最大角对最大角,最小角对最小角.
③相等的边(角)为对应边(角).
知2-讲
(2) 位置关系法:
①公共角(对顶角)为对应角,公共边为对应边.
②对应角的对边为对应边,两个对应角所夹的边是对应边.
③对应边的对角为对应角,两条对应边所夹的角是对应角.
(3) 字母顺序法:
根据书写规范按照对应顶点确定对应边或对应角 .
知2-讲
特别解读
对应关系可从两个方面理解 .
(1)从动态角度理解:重合是找对应元素的关键 .
(2)从静态角度理解:
从表示方法中找准对应顶点,然后确定对应边和对应角 .
知2-练
如图 14.1-4,已知△ ABD ≌△ CDB,∠ ABD= ∠ CDB. 写出其对应边和对应角 .
例2
知2-练
解题秘方:根据图形的位置特征确定对应边和对应角 .
解:BD 与 DB, AD 与 CB, AB 与 CD 是对应边;∠ A 与∠ C,∠ ABD 与∠ CDB,∠ ADB 与
∠ CBD 是对应角 .
解法提醒
利用图形的位置特征确定对应边和对应角时,要抓住对应边所对的角是对应角,对应角所对的边是对应边;当全等三角形的两组对应边(角)已确定时,剩下的一组边(角)就是对应边(角).
知2-练
知2-练
如图 14.1-5,将△ ABC 绕其顶点 B 顺时针旋转一定角度后得到△ DBE,请说出图中△ ABC 和△ DBE 是否为全等三角形,若是,写出其对应边和对应角 .
例3
知2-练
解题秘方:根据图形旋转前后的对应位置找对应元素 .
解:△ ABC ≌ △ DBE. AB 与 DB, AC 与 DE, BC 与 BE是对应边,∠ A 与∠ BDE,∠ ABC 与∠ DBE,
∠ C 与∠ E 是对应角 .
解法提醒
从动态的角度找对应元素,关键抓住图形变换前后的重合元素,重合的边为对应边,重合的角为对应角 .
知2-练
知3-讲
知识点
全等三角形的性质
3
知3-讲
2. 拓展 全等三角形的对应元素相等 .
全等三角形中的对应元素包括对应边、对应角、对应边上的中线、对应边上的高、对应角的平分线、周长、面积等 .
知3-讲
要点提醒
1. 应用全等三角形的性质时,要先确定两个条件:
(1)两个三角形全等;
(2)找对应元素 .
2. 全等三角形的性质是证明线段、角相等的常用方法.
知3-练
如图 14.1-6,已知△ ABF ≌△ CDE.
(1)若∠ B=38°,∠ DCF=42°,求∠ EFC 的度数;
(2)若 BD=10, EF=2,求 BF 的长.
例4
知3-练
解题秘方:利用全等三角形的对应边相等和对应角相等解决问题 .
解:(1) ∵△ ABF ≌△ CDE,
∴∠ D= ∠ B=38°,
∴∠ EFC= ∠ DCF+ ∠ D=42° +38° =80° .
解法提醒
全等三角形的对应边(对应角)相等,由此可得两条线段(两个角)相等,从而进一步说明线段(角)的相等关系、和差关系或求线段的长度、角的大小 .
知3-练
知3-练
证明: (2) ∵△ ABF ≌△ CDE,∴ BF=DE,
∴ BF-EF=DE-EF,即 BE=DF.
∵ BD=10, EF=2,
∴ BE=(10-2)÷2=4,
∴ BF=BE+EF=4+2=6.
知3-练
如图 14.1-7,已知 Rt △ ABC ≌ Rt △ CDE,且点 B, C,D 在同一条直线上,试判断 AC 与 CE 的位置关系,并给予证明 .
例5
方法点拨
证线段位置关系的方法:
证线段与线段的位置关系通常考虑平行、垂直两种特殊关系,证平行的方法是转化为证明同位角相等、内错角相等或同旁内角互补;证垂直的方法是转化为证明它们的夹角为90° 或三角形的两内角互余.
知3-练
知3-练
解题秘方:通过求 AC, CE 夹角的度数判断其位置关系 .
知3-练
解: AC ⊥ CE.
证明如下:∵ Rt △ ABC ≌ Rt △ CDE,
∴∠ BAC= ∠ DCE.
∵∠ BAC+ ∠ ACB=90°,∴∠ DCE+ ∠ ACB=90°.
∴∠ ACE=180°- (∠ DCE+ ∠ ACB)=180°-90°=90°.
∴ AC ⊥ CE.
全等三角形
全等形
特例
全等三角形
性质
对应元素
