13.1.3三角形中几条重要线段(2)课件(共34张PPT)
文档属性
| 名称 | 13.1.3三角形中几条重要线段(2)课件(共34张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-07 22:28:23 | ||
图片预览



文档简介
(共34张PPT)
复习回顾
定义 图示
垂线
线段中点
角平分线
O
B
A
A
B
当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线
把一条线段分成两条相等的线段的点
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线
这里有一块三角形的蛋糕,如果兄弟两个想要平分的话,你该怎么办呢?
情境引入
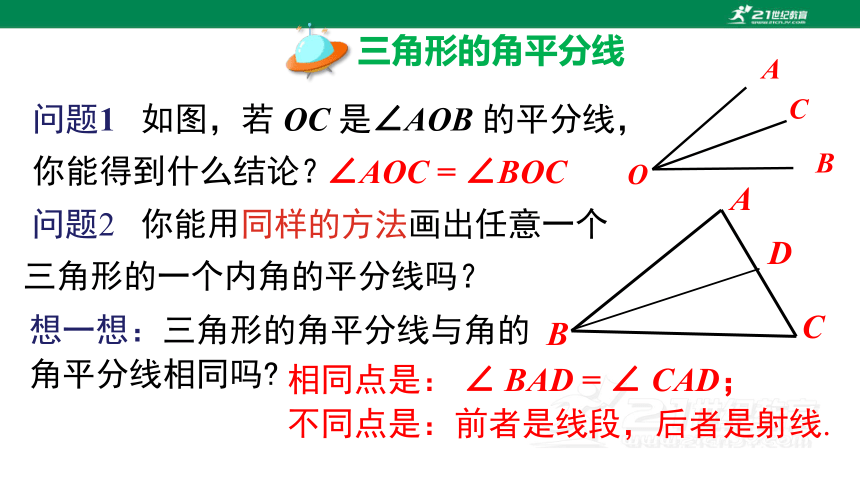
问题1 如图,若 OC 是∠AOB 的平分线,你能得到什么结论?
A
C
B
O
∠AOC = ∠BOC
问题2 你能用同样的方法画出任意一个三角形的一个内角的平分线吗?
A
B
C
D
想一想:三角形的角平分线与角的角平分线相同吗
相同点是: ∠ BAD = ∠ CAD;
不同点是:前者是线段,后者是射线.
三角形的角平分线
B
A
C
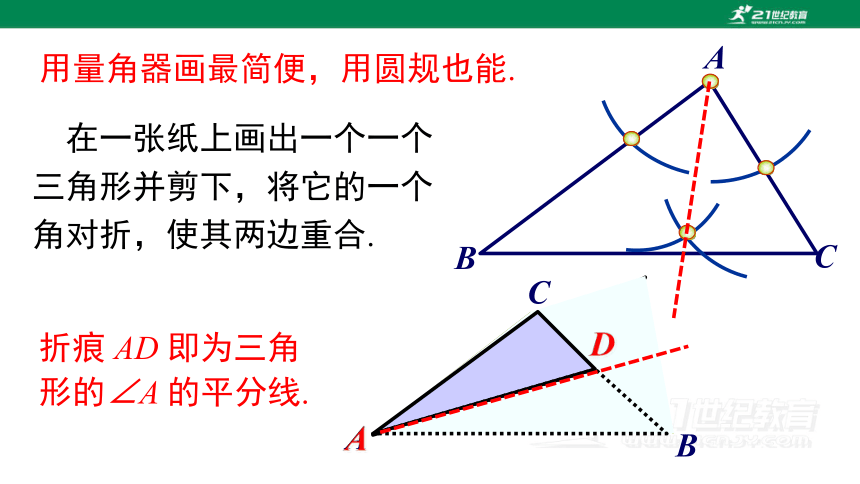
用量角器画最简便,用圆规也能.
在一张纸上画出一个一个三角形并剪下,将它的一个角对折,使其两边重合.
折痕 AD 即为三角形的∠A 的平分线.
A
B
C
A
D
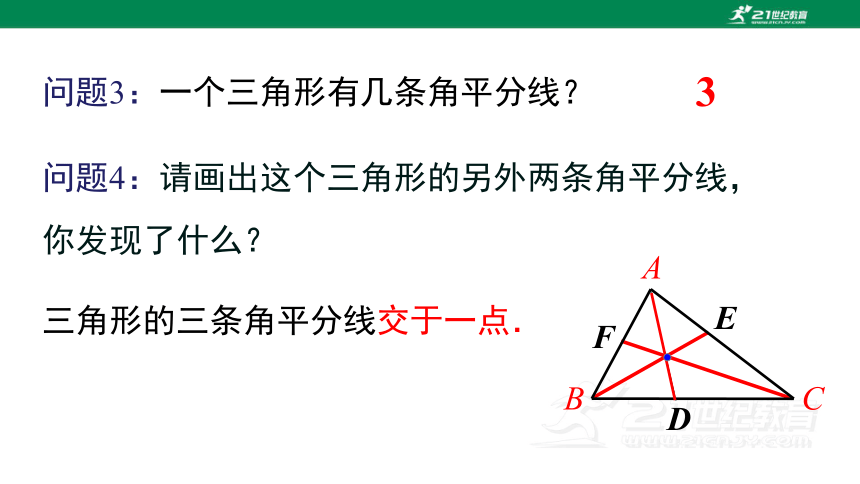
问题4:请画出这个三角形的另外两条角平分线,你发现了什么?
三角形的三条角平分线交于一点.
A
B
C
D
E
F
问题3:一个三角形有几条角平分线?
3
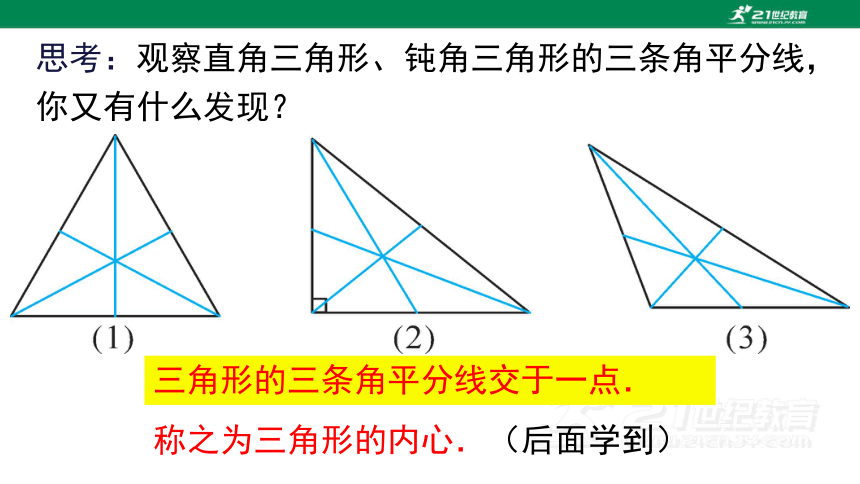
思考:观察直角三角形、钝角三角形的三条角平分线,你又有什么发现?
三角形的三条角平分线交于一点.
称之为三角形的内心.(后面学到)
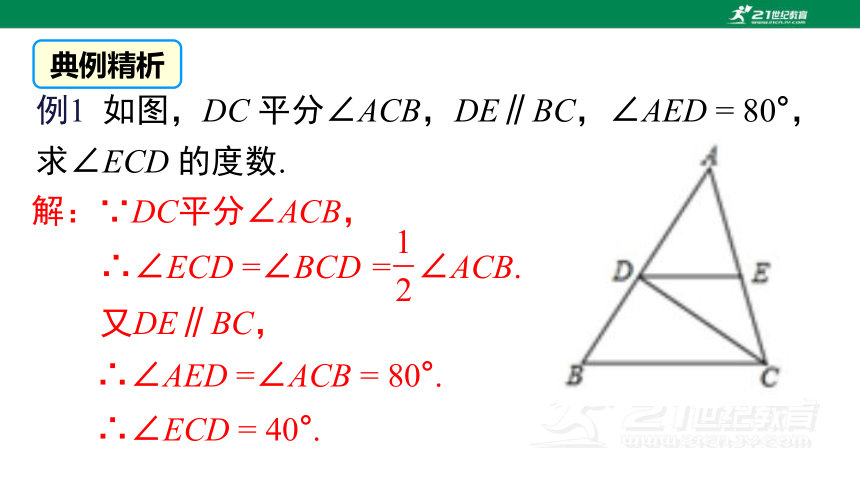
例1 如图,DC 平分∠ACB,DE∥BC,∠AED = 80°,求∠ECD 的度数.
解:∵DC平分∠ACB,
又DE∥BC,
典例精析
∴∠AED =∠ACB = 80°.
∴∠ECD = 40°.
∴∠ECD =∠BCD = ∠ACB.
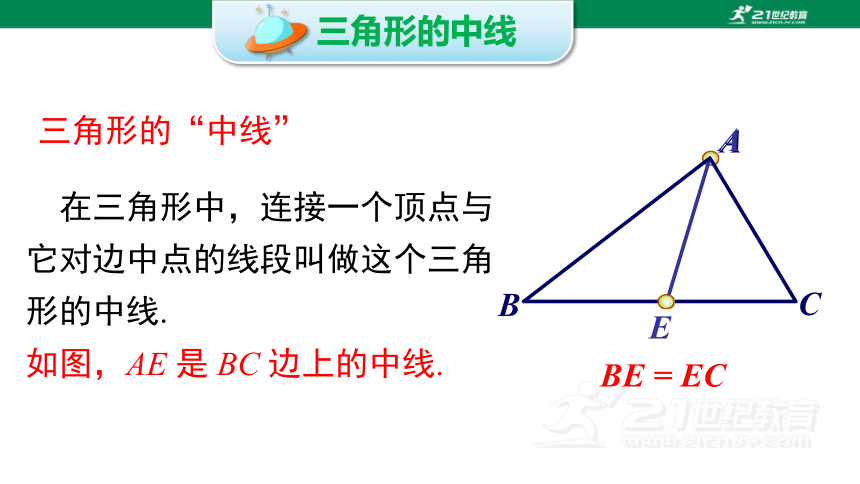
在三角形中,连接一个顶点与它对边中点的线段叫做这个三角形的中线.
如图,AE 是 BC 边上的中线.
三角形的“中线”
B
A
C
A
BE = EC
E
三角形的中线
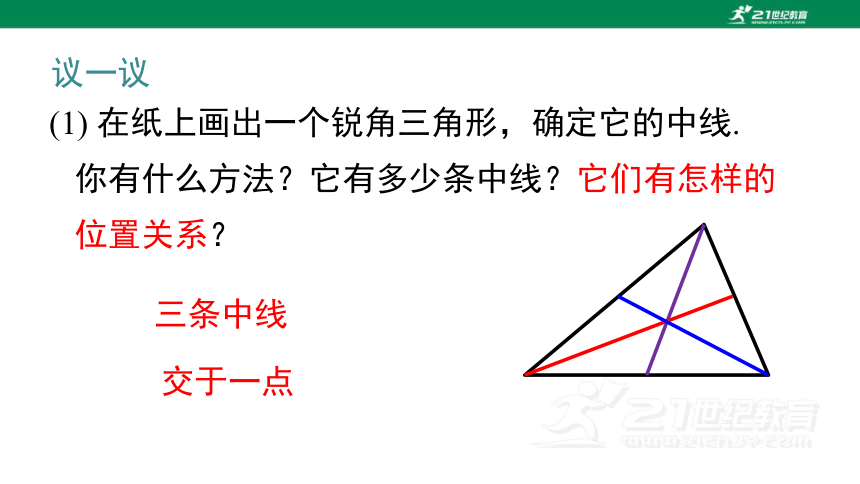
(1) 在纸上画出一个锐角三角形,确定它的中线.
你有什么方法?它有多少条中线?它们有怎样的
位置关系?
三条中线
交于一点
议一议
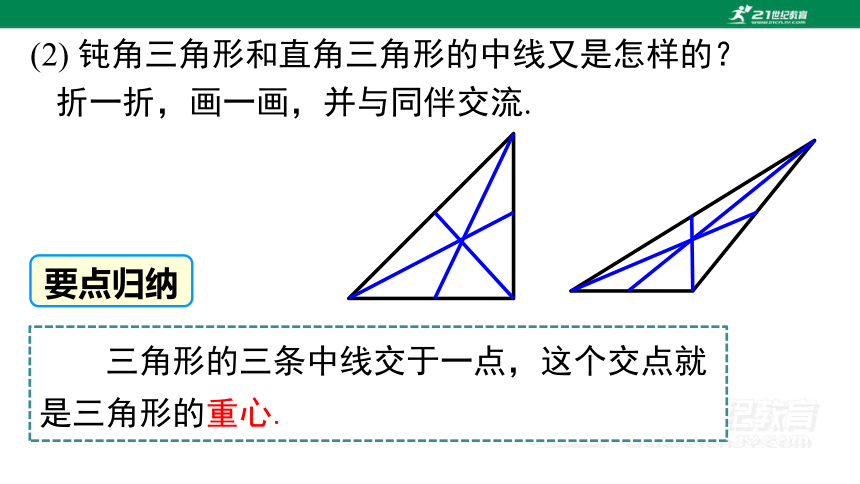
(2) 钝角三角形和直角三角形的中线又是怎样的?
折一折,画一画,并与同伴交流.
三角形的三条中线交于一点,这个交点就是三角形的重心.
要点归纳
典例精析
例2 在△ABC 中,AC=5cm,AD 是△ABC 的中线,若△ABD 的周长比△ADC 的周长大 2 cm,则 BA=____cm.
提示:将△ABD 与△ADC 的周长之差转化为边长的差.
7
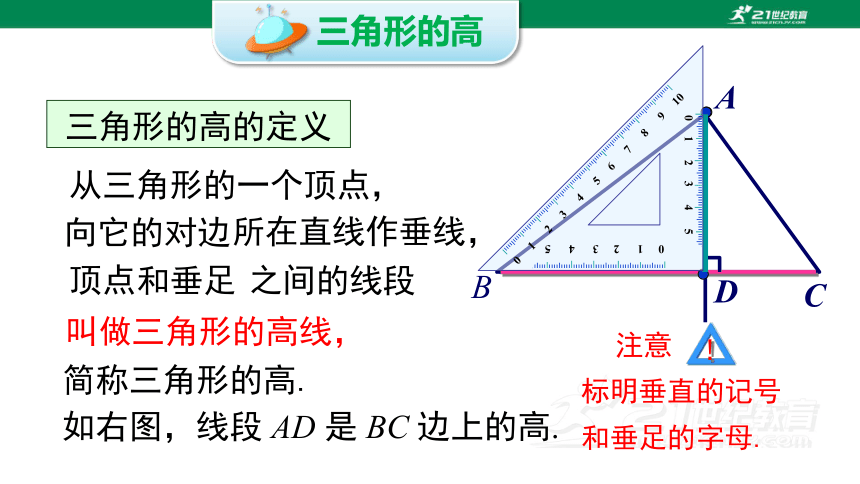
三角形的高的定义
从三角形的一个顶点,
向它的对边
A
B
C
所在直线作垂线,
顶点
和垂足
D
之间的线段
叫做三角形的高线,
简称三角形的高.
如右图,线段 AD 是 BC 边上的高.
和垂足的字母.
注意
!
标明垂直的记号
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
三角形的高
思考:你还能画出一条高来吗?
一个三角形有三个顶点,应该有三条高.
(1) 你能画出三角形的三条高吗?
(2) 这三条高之间有怎样的位置关系?
O
(3) 锐角三角形的三条高是在三角
形的内部还是外部?
锐角三角形的三条高交于同一点.
锐角三角形的三条高都在三角形的内部.
锐角三角形的三条高
如图所示.
直角边 BC 边上的高是 ;
直角边 AB 边上的高是 ;
(2) AC 边上的高是 ;
直角三角形的三条高
A
B
C
(1) 画出直角三角形的三条高,
AB
BC
它们有怎样的位置关系?
D
直角三角形的三条高交于直角顶点.
BD
钝角三角形的三条高
(1) 你能画出钝角三角形的三条高吗?
A
B
C
D
E
F
(2) AC 边上的高呢?
AB 边上呢?
BC 边上呢?
BF
CE
AD
A
B
C
D
F
(3)钝角三角形的三条高
交于一点吗?
(4)它们所在的直线交于
一点吗?
O
E
钝角三角形的三条高
不相交于一点.
钝角三角形的三条高所在直线交于一点.
例3 作△ABC 的边 AB 上的高,下列作法中,正确的是( )
方法总结:三角形任意一边上的高必须满足:(1)过该边所对的顶点;(2)垂足必须在该边或在该边的延长线上.
D
例4 如图所示,在△ABC 中,AB=AC=5,BC=6,AD⊥BC 于点 D,且 AD=4,若点 P 在边 AC 上移动,则 BP 的最小值为____.
方法总结:可利用面积相等作桥梁(但不求面积)
求三角形的高,此解题方法通常称为“面积法”.
例5 如图,已知 AD 是△ABC 的角平分线,CE 是△ABC 的高,∠BAC=60°,∠BCE=40°,求∠ADB 的度数.
解:因为 AD 是△ABC 的角平分线,∠BAC=60°,
所以∠DAC=∠BAD=30°.
因为 CE 是△ABC 的高,∠BCE=40°,
所以∠B=50°.
所以∠ADB=180°-∠B-∠BAD
=180°-30°-50°=100°.
例6 如图,△ABC 中,AD 是 BC 边上的中线,若△ABC 的周长为 35 cm,BC = 11 cm,且△ABD 与△ACD 的周长差为 3 cm,求 AB 与 AC 的长.
A
C
D
B
解: ∵AD 是△ABC 的中线,
∴CD = BD.
∵△ABC 的周长为 35 cm,BC = 11cm,
∴AC + AB = 35 - 11 = 24(cm).
又∵△ABD 与△ACD 的周长差为 3 cm,∴AB - AC = 3 cm,
∴AB = 13.5 cm,AC = 10.5 cm.
有关三角形的高、角平分线、中线的计算
A
C
D
B
解:因为 AD 是△ABC 的中线,
所以 CD = BD.
因为△ABC 的周长为 35 cm,
BC = 11cm,
所以 AC + AB = 35 - 11 = 24 (cm).
又因为△ABD 与△ACD 的周长差为 3 cm,
所以 AB - AC = 3 cm,
所以 AB = 13.5 cm,AC = 10.5 cm.
例7 如图,在△ABC 中,E 是 BC 上的一点,EC=2BE,点 D 是 AC 的中点,S△ABC=12,求 S△ADF-S△BEF 的值.
因为 S△ABD-S△ABE=(S△ADF+S△ABF)-(S△ABF+S△BEF)=S△ADF-S△BEF,
所以 S△ADF-S△BEF=S△ABD-S△ABE=6-4=2.
解:因为点 D 是 AC 的中点,所以AD= AC.
因为 S△ABC=12,所以S△ABD= S△ABC= ×12=6.
因为EC=2BE,S△ABC=12,∴S△ABE= S△ABC=4.
三角形的
重要线段 概念 图形 表示法
三角形的
角平分线
三角形中,一个角的平分线与这个角对边相交,顶点与交点之间的线段 因为AD是△ABC的高,所以AD⊥BC,
∠ADB=∠ADC=90°.
三角形
的中线 三角形中,连接一个顶点与它对边中点的线段
三角形
的高线 从三角形的一个顶点到它对边所在的直线的垂线段
知识归纳
A
B
C
D
A
B
C
D
A
B
C
D
观察下列语句:
1. 无限不循环小数叫做无理数;
2. 两条边相等的三角形叫做等腰三角形;
3. 三角形中,一个角的平分线与这个角对边相交,顶点与交点之间的线段叫做三角形的角平分线.
像这样能明确界定某个对象含义的语句叫做定义.
请你举出你所熟知的一些定义例子.
定义
例如:
1.“具有中华人民共和国国籍的人,叫做中华人民共和国公民” 是“中华人民共和国公民”的定义;
2. “两点之间线段的长度,叫做这两点之间的距离” 是“两点之间的距离”的定义;
3.“在一个方程中,只含有一个未知数,并且未知数的指数是1,这样的方程叫做一元一次方程” 是“一元一次方程”的定义.
1.下列说法正确的是( )
A.三角形三条高都在三角形内
B.三角形三条中线相交于一点
C.三角形的三条角平分线可能在三角形内,也可
能在三角形外
D.三角形的角平分线是射线
B
2.在△ABC 中,AD 为中线,BE 为角平分线,则在以下等式中:①∠BAD =∠CAD;②∠ABE =∠CBE;③BD = DC;④AE = EC.其中正确的是( )
A.①②
B.③④
C.①④
D.②③
D
A
B
C
D
E
3.如图,△ABC 中∠C = 90°,CD⊥AB,图中线段中可以作为△ABC 的高的有 ( )
A.2 条 B.3 条
C.4 条 D.5 条
4.下列各组图形中,哪一组图形中 AD 是△ABC 的 BC 边上的高 ( )
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
A.
B.
C.
D.
B
D
5.填空:
(1) 如图①,AD,BE,CF 是△ABC 的三条中线,则
AB = 2__,BD = __,AE = __ .
(2) 如图②,AD,BE,CF 是△ABC 的三条角平分线,
则∠1 =_______, ∠3 =_______,∠ABC = 2_____.
图①
图②
AF
DC
∠CAD
∠2
∠BCF
A
B
C
D
E
F
AC
解:因为 CD 是△ABC 的中线,
所以 BD = AD.
因为 BC - AC = 5cm,
所以△DBC 与△ADC 的周长差是 5 cm.
又因为△DBC 的周长为 25 cm,
所以△ADC 的周长为 25 - 5 = 20 (cm).
6. 如图,在△ABC 中,CD 是中线,已知 BC - AC = 5 cm, △DBC 的周长为 25 cm,求△ADC 的周长.
A
D
B
C
7. 如图,AE 是△ABC 的角平分线.已知∠B = 45°, ∠C = 60°,求∠BAE 和∠AEB 的度数.
A
B
C
E
解:因为 AE 是△ABC 的角平分线,
因为 ∠BAC +∠B +∠C = 180°,
所以∠BAC = 180°-∠B-∠C = 180°-45°-60° = 75°.所以∠CAE = ∠BAE = 37.5°.
因为 ∠AEC = 180°-∠CAE -∠C = 82.5°,
所以∠AEB = 180°-∠AEC = 180°-82.5° = 97.5°.
所以 ∠CAE = ∠BAE = ∠BAC.
8.如图,在△ABC 中,AD 是△ABC 的高,AE 是△ABC 的角平分线,已知∠BAC = 82°,∠C = 40°,求∠DAE 的大小.
解: 因为 AD 是△ABC 的高,
所以 ∠ADC=90°.
因为 ∠ADC +∠C +∠DAC = 180°,
所以 ∠DAC=180°-(∠ADC+∠C )
=180°-90°-40°=50°.
因为 AE 是△ABC 的角平分线,∠BAC = 82°,
所以∠CAE = 41°.
所以∠DAE =∠DAC-∠CAE = 50°-41° = 9°.
B
A
C
D
E
三角形重要线段
高
钝角三角形两短边上的高的画法
中线
会把原三角形面积平分
一边上的中线把原三角形分成两个三角形,这两个三角形的周长差等于原三角形其余两边的差
角平分线
定义
复习回顾
定义 图示
垂线
线段中点
角平分线
O
B
A
A
B
当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线
把一条线段分成两条相等的线段的点
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线
这里有一块三角形的蛋糕,如果兄弟两个想要平分的话,你该怎么办呢?
情境引入
问题1 如图,若 OC 是∠AOB 的平分线,你能得到什么结论?
A
C
B
O
∠AOC = ∠BOC
问题2 你能用同样的方法画出任意一个三角形的一个内角的平分线吗?
A
B
C
D
想一想:三角形的角平分线与角的角平分线相同吗
相同点是: ∠ BAD = ∠ CAD;
不同点是:前者是线段,后者是射线.
三角形的角平分线
B
A
C
用量角器画最简便,用圆规也能.
在一张纸上画出一个一个三角形并剪下,将它的一个角对折,使其两边重合.
折痕 AD 即为三角形的∠A 的平分线.
A
B
C
A
D
问题4:请画出这个三角形的另外两条角平分线,你发现了什么?
三角形的三条角平分线交于一点.
A
B
C
D
E
F
问题3:一个三角形有几条角平分线?
3
思考:观察直角三角形、钝角三角形的三条角平分线,你又有什么发现?
三角形的三条角平分线交于一点.
称之为三角形的内心.(后面学到)
例1 如图,DC 平分∠ACB,DE∥BC,∠AED = 80°,求∠ECD 的度数.
解:∵DC平分∠ACB,
又DE∥BC,
典例精析
∴∠AED =∠ACB = 80°.
∴∠ECD = 40°.
∴∠ECD =∠BCD = ∠ACB.
在三角形中,连接一个顶点与它对边中点的线段叫做这个三角形的中线.
如图,AE 是 BC 边上的中线.
三角形的“中线”
B
A
C
A
BE = EC
E
三角形的中线
(1) 在纸上画出一个锐角三角形,确定它的中线.
你有什么方法?它有多少条中线?它们有怎样的
位置关系?
三条中线
交于一点
议一议
(2) 钝角三角形和直角三角形的中线又是怎样的?
折一折,画一画,并与同伴交流.
三角形的三条中线交于一点,这个交点就是三角形的重心.
要点归纳
典例精析
例2 在△ABC 中,AC=5cm,AD 是△ABC 的中线,若△ABD 的周长比△ADC 的周长大 2 cm,则 BA=____cm.
提示:将△ABD 与△ADC 的周长之差转化为边长的差.
7
三角形的高的定义
从三角形的一个顶点,
向它的对边
A
B
C
所在直线作垂线,
顶点
和垂足
D
之间的线段
叫做三角形的高线,
简称三角形的高.
如右图,线段 AD 是 BC 边上的高.
和垂足的字母.
注意
!
标明垂直的记号
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
三角形的高
思考:你还能画出一条高来吗?
一个三角形有三个顶点,应该有三条高.
(1) 你能画出三角形的三条高吗?
(2) 这三条高之间有怎样的位置关系?
O
(3) 锐角三角形的三条高是在三角
形的内部还是外部?
锐角三角形的三条高交于同一点.
锐角三角形的三条高都在三角形的内部.
锐角三角形的三条高
如图所示.
直角边 BC 边上的高是 ;
直角边 AB 边上的高是 ;
(2) AC 边上的高是 ;
直角三角形的三条高
A
B
C
(1) 画出直角三角形的三条高,
AB
BC
它们有怎样的位置关系?
D
直角三角形的三条高交于直角顶点.
BD
钝角三角形的三条高
(1) 你能画出钝角三角形的三条高吗?
A
B
C
D
E
F
(2) AC 边上的高呢?
AB 边上呢?
BC 边上呢?
BF
CE
AD
A
B
C
D
F
(3)钝角三角形的三条高
交于一点吗?
(4)它们所在的直线交于
一点吗?
O
E
钝角三角形的三条高
不相交于一点.
钝角三角形的三条高所在直线交于一点.
例3 作△ABC 的边 AB 上的高,下列作法中,正确的是( )
方法总结:三角形任意一边上的高必须满足:(1)过该边所对的顶点;(2)垂足必须在该边或在该边的延长线上.
D
例4 如图所示,在△ABC 中,AB=AC=5,BC=6,AD⊥BC 于点 D,且 AD=4,若点 P 在边 AC 上移动,则 BP 的最小值为____.
方法总结:可利用面积相等作桥梁(但不求面积)
求三角形的高,此解题方法通常称为“面积法”.
例5 如图,已知 AD 是△ABC 的角平分线,CE 是△ABC 的高,∠BAC=60°,∠BCE=40°,求∠ADB 的度数.
解:因为 AD 是△ABC 的角平分线,∠BAC=60°,
所以∠DAC=∠BAD=30°.
因为 CE 是△ABC 的高,∠BCE=40°,
所以∠B=50°.
所以∠ADB=180°-∠B-∠BAD
=180°-30°-50°=100°.
例6 如图,△ABC 中,AD 是 BC 边上的中线,若△ABC 的周长为 35 cm,BC = 11 cm,且△ABD 与△ACD 的周长差为 3 cm,求 AB 与 AC 的长.
A
C
D
B
解: ∵AD 是△ABC 的中线,
∴CD = BD.
∵△ABC 的周长为 35 cm,BC = 11cm,
∴AC + AB = 35 - 11 = 24(cm).
又∵△ABD 与△ACD 的周长差为 3 cm,∴AB - AC = 3 cm,
∴AB = 13.5 cm,AC = 10.5 cm.
有关三角形的高、角平分线、中线的计算
A
C
D
B
解:因为 AD 是△ABC 的中线,
所以 CD = BD.
因为△ABC 的周长为 35 cm,
BC = 11cm,
所以 AC + AB = 35 - 11 = 24 (cm).
又因为△ABD 与△ACD 的周长差为 3 cm,
所以 AB - AC = 3 cm,
所以 AB = 13.5 cm,AC = 10.5 cm.
例7 如图,在△ABC 中,E 是 BC 上的一点,EC=2BE,点 D 是 AC 的中点,S△ABC=12,求 S△ADF-S△BEF 的值.
因为 S△ABD-S△ABE=(S△ADF+S△ABF)-(S△ABF+S△BEF)=S△ADF-S△BEF,
所以 S△ADF-S△BEF=S△ABD-S△ABE=6-4=2.
解:因为点 D 是 AC 的中点,所以AD= AC.
因为 S△ABC=12,所以S△ABD= S△ABC= ×12=6.
因为EC=2BE,S△ABC=12,∴S△ABE= S△ABC=4.
三角形的
重要线段 概念 图形 表示法
三角形的
角平分线
三角形中,一个角的平分线与这个角对边相交,顶点与交点之间的线段 因为AD是△ABC的高,所以AD⊥BC,
∠ADB=∠ADC=90°.
三角形
的中线 三角形中,连接一个顶点与它对边中点的线段
三角形
的高线 从三角形的一个顶点到它对边所在的直线的垂线段
知识归纳
A
B
C
D
A
B
C
D
A
B
C
D
观察下列语句:
1. 无限不循环小数叫做无理数;
2. 两条边相等的三角形叫做等腰三角形;
3. 三角形中,一个角的平分线与这个角对边相交,顶点与交点之间的线段叫做三角形的角平分线.
像这样能明确界定某个对象含义的语句叫做定义.
请你举出你所熟知的一些定义例子.
定义
例如:
1.“具有中华人民共和国国籍的人,叫做中华人民共和国公民” 是“中华人民共和国公民”的定义;
2. “两点之间线段的长度,叫做这两点之间的距离” 是“两点之间的距离”的定义;
3.“在一个方程中,只含有一个未知数,并且未知数的指数是1,这样的方程叫做一元一次方程” 是“一元一次方程”的定义.
1.下列说法正确的是( )
A.三角形三条高都在三角形内
B.三角形三条中线相交于一点
C.三角形的三条角平分线可能在三角形内,也可
能在三角形外
D.三角形的角平分线是射线
B
2.在△ABC 中,AD 为中线,BE 为角平分线,则在以下等式中:①∠BAD =∠CAD;②∠ABE =∠CBE;③BD = DC;④AE = EC.其中正确的是( )
A.①②
B.③④
C.①④
D.②③
D
A
B
C
D
E
3.如图,△ABC 中∠C = 90°,CD⊥AB,图中线段中可以作为△ABC 的高的有 ( )
A.2 条 B.3 条
C.4 条 D.5 条
4.下列各组图形中,哪一组图形中 AD 是△ABC 的 BC 边上的高 ( )
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
A.
B.
C.
D.
B
D
5.填空:
(1) 如图①,AD,BE,CF 是△ABC 的三条中线,则
AB = 2__,BD = __,AE = __ .
(2) 如图②,AD,BE,CF 是△ABC 的三条角平分线,
则∠1 =_______, ∠3 =_______,∠ABC = 2_____.
图①
图②
AF
DC
∠CAD
∠2
∠BCF
A
B
C
D
E
F
AC
解:因为 CD 是△ABC 的中线,
所以 BD = AD.
因为 BC - AC = 5cm,
所以△DBC 与△ADC 的周长差是 5 cm.
又因为△DBC 的周长为 25 cm,
所以△ADC 的周长为 25 - 5 = 20 (cm).
6. 如图,在△ABC 中,CD 是中线,已知 BC - AC = 5 cm, △DBC 的周长为 25 cm,求△ADC 的周长.
A
D
B
C
7. 如图,AE 是△ABC 的角平分线.已知∠B = 45°, ∠C = 60°,求∠BAE 和∠AEB 的度数.
A
B
C
E
解:因为 AE 是△ABC 的角平分线,
因为 ∠BAC +∠B +∠C = 180°,
所以∠BAC = 180°-∠B-∠C = 180°-45°-60° = 75°.所以∠CAE = ∠BAE = 37.5°.
因为 ∠AEC = 180°-∠CAE -∠C = 82.5°,
所以∠AEB = 180°-∠AEC = 180°-82.5° = 97.5°.
所以 ∠CAE = ∠BAE = ∠BAC.
8.如图,在△ABC 中,AD 是△ABC 的高,AE 是△ABC 的角平分线,已知∠BAC = 82°,∠C = 40°,求∠DAE 的大小.
解: 因为 AD 是△ABC 的高,
所以 ∠ADC=90°.
因为 ∠ADC +∠C +∠DAC = 180°,
所以 ∠DAC=180°-(∠ADC+∠C )
=180°-90°-40°=50°.
因为 AE 是△ABC 的角平分线,∠BAC = 82°,
所以∠CAE = 41°.
所以∠DAE =∠DAC-∠CAE = 50°-41° = 9°.
B
A
C
D
E
三角形重要线段
高
钝角三角形两短边上的高的画法
中线
会把原三角形面积平分
一边上的中线把原三角形分成两个三角形,这两个三角形的周长差等于原三角形其余两边的差
角平分线
定义
