13.2 第1课时 命题 课件(共29张PPT)
文档属性
| 名称 | 13.2 第1课时 命题 课件(共29张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-07 22:39:35 | ||
图片预览







文档简介
(共29张PPT)
小华与小刚正在津津有味地阅读《我们爱科学》.
这个黑客终于被逮住了.
是的,现在的因特网广泛运用于我们的生活中,给我们带来了方便,但……
这个黑客是个小偷.
是个喜欢穿黑衣服的贼.
坐在旁边的两个人一边听着他们的谈话,一边也在悄悄地议论着.
小明的百米成绩有进步,已达到9秒9.
好!继续努力,争取超过10秒.
不要再抢啦!每人发一个球!
有一位田径教练向领导汇报训练成绩:
相传,阎锡山在观看士兵篮球赛时,双方争抢非常激烈,于是命令:
2. 如果一个句子没有对某一件事情作出任何判断,那 么它就不是命题.
如:画线段 AB = CD.
1. 只要对一件事情作出了判断,不管正确与否,都是命题.
如:相等的角是对顶角.
注意:
像这样,对某一件事件作出正确或不正确判断的语句(或式子)叫做命题.
一、命题的概念
命题的定义与结构
例1 判断下列四个语句中,哪个是命题, 哪个不是命题?并说明理由:
(1)对顶角相等吗?
(2)画一条线段 AB = 2cm;
(3)两条直线平行,同位角相等;
(4)相等的两个角,一定是对顶角.
典例精析
解:(3)(4)是命题,(1)(2)不是命题.
理由如下:(1)是问句,故不是命题;(2)是做一件事情,也不是命题.
2)两条直线相交,有且只有一个交点( )
5)取线段 AB 的中点 C ( )
1)长度相等的两条线段是相等的线段吗?( )
6)画两条相等的线段( )
练一练:判断下列语句是不是命题?是用“√”,
不是用“× 表示.
3)不相等的两个角不是对顶角( )
4)相等的两个角是对顶角( )
×
√
×
×
√
√
观察下列命题,你能发现这些命题有什么共同的结构特
征?与同伴交流.
(1)如果两个三角形的三条边相等,那么这两个三角形的周长相等;
(2)如果两个数的绝对值相等,那么这两个数也相等;
(3)如果一个数的平方等于 9,那么这个数是 3.
都是“如果……那么……”的形式
二、命题的结构
命题一般都可以写成“如果 p,那么 q”的形式.
1. 其中 p 是这个命题的条件(题设),
2. q 是这个命题的结论(题断).
如命题:熊猫没有翅膀.改写为:
如果这个动物是熊猫,那么它就没有翅膀.
注意:添加“如果”“那么”后,命题的意义不能改变,改写的句子要完整,语句要通顺,使命题的题设和结论更明朗,易于分辨,改写过程中,要适当增加词语,切不可生搬硬套.
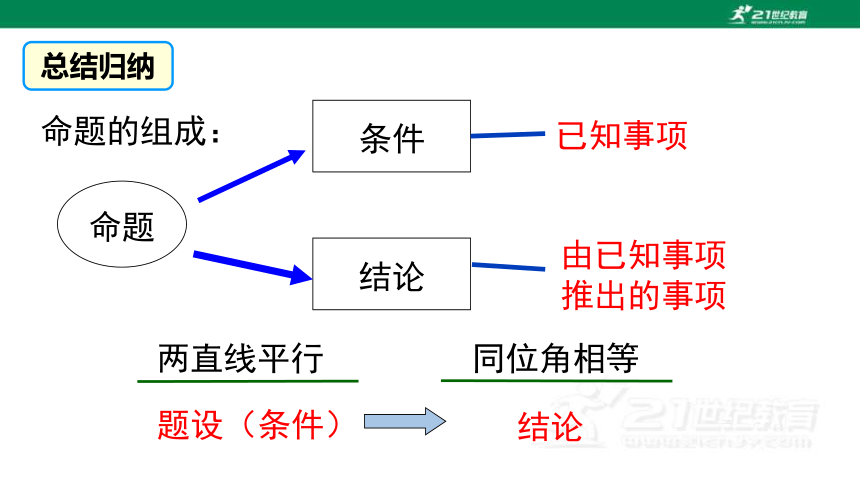
命题
条件
结论
已知事项
由已知事项推出的事项
两直线平行 同位角相等
题设(条件)
结论
命题的组成:
总结归纳
例2 指出下列命题的条件与结论.
(1) 两条直线都平行于同一条直线,这两条直线平行;
(2) 如果∠A =∠B,那么∠A 的补角与∠B 的补角相等.
解 : (1)“两条直线都平行于同一条直线”是条件,“两条直线平行”是结论.
(2)“∠A =∠B”是条件,“∠A 的补角与∠B 的补角相等”是结论.
把下列命题改写成“如果……那么……”的形式.并指出它的条件和结论.
1. 对顶角相等; 2. 内错角相等;
3. 两直线被第三条直线所截,同位角相等;
4. 同平行于一直线的两直线平行; 5. 等角的补角相等.
练一练
解:(1) 如果有两个角是对顶角,那么这两个角相等.
条件:有两个角是对顶角,结论:这两个角相等.
(2) 如果有两个角是内错角,那么这两个角相等.
条件:有两个角是内错角,结论:这两个角相等.
(3) 如果有两直线被第三条直线所截形成三线八角,
那么其同位角相等;
条件:有两直线被第三条直线所截形成三线八角,
结论:其同位角相等.
(4) 如果有两直线平行于同一直线,那么这两直线平行.
条件:有两直线平行于同一直线,
结论:这这两直线平行.
(5) 如果有两个角是相等,那么这两角的补角也相等.
条件:有两个角是相等,结论:这两角的补角也相等.
特别规定:
正确的命题叫真命题,错误的命题叫假命题.
命题1:“如果一个数能被 4 整除,那么它也能被 2 整除”
观察下列命题,你能发现这些命题有什么不同的特点吗?
命题 1 是一个正确的命题;命题 2 是一个错误的命题.
命题2:“如果两个角互补,那么它们是邻补角”
真命题与假命题
(1)同旁内角互补( )
(4)两点可以确定一条直线( )
(2)一个角的补角大于这个角( )
判断下列命题的真假.真的用“√”,假的用“×”表示.
(5)两点之间线段最短( )
(3)相等的两个角是对顶角( )
×
(6)同角的余角相等( )
×
√
√
√
×
练一练
做一做:指出下列命题的条件和结论,并改写成“如果 p,那么 q”的形式:
命题 条件(如果 p) 结论(那么 q)
①能被 2 整除的数是偶数
②有公共顶点的两个角是对顶角
这个数是偶数
一个数能被 2 整除
这两个角是对顶角
两个角有公共顶点
逆命题
命题 条件(如果 p) 结论(那么 q)
③两直线平行,同位角相等
④同位角相等,两直线平行
直线所截的同位角相等
两条平行线被第三条直线所截
这两条直线平行
如果两条直线被第三条直线所截的同位角相等
上述命题 ③ 与 ④ 的条件与结论之间有什么联系?
③两直线平行,同位角相等.
④同位角相等,两直线平行.
命题③与④的条件与结论互换了位置.
将命题“如果 p,那么 q”中的结论和条件互换,便得到一个新命题“如果 p,那么 q”,我们把这样的两个命题称为互逆命题,其中一个叫做原命题,另一个叫做原命题的逆命题.
例如,上述命题 ③ 与 ④ 就是互逆命题.
从上我们可以看出,只要将一个命题的条件和结论互换,就可得到它的逆命题,所以每个命题都有逆命题.
你还能举出其它的例子吗?
写出下列命题的逆命题:
(1)若两数相等,则它们的绝对值也相等;
(2)如果 m 是整数,那么它也是有理数;
(3)两直线平行,内错角相等;
(4)两边相等的三角形是等腰三角形.
绝对值相等的两个数相等.
如果 m 是有理数,那么它也是整数.
内错角相等,两直线平行.
等腰三角形的两边相等.
练一练
写出下列命题的逆命题,并判断它们的真假.
(1)如果 a = b,则 a2 = b2;
(2)等角的余角相等;
(3)同位角相等,两直线平行.
(1)如果 a2 = b2 ,则 a = b,假命题.
(2)如果两个角的余角相等,那么这两个角也相等, 真命题.
(3)两直线平行,同位角相等,真命题.
思考:原命题是真命题,那么它的逆命题也是真命题吗?
解:
反例
“因为早上我发现老张从玉米地那边过来,把一袋东西背回家,还发现我地里的玉米被人捌了,我知道老张家没有种玉米.所以我家玉米肯定是老张捌的.”
片段1:一天早上,李老汉来到衙门里告状说:老张刚刚在他地里偷捌(同扒)了一袋子玉米.吕县令立即派衙役将老张拘捕到县衙审讯:
吕县令问李老汉:“你怎知是老张偷了你的玉米 ”
这种从已知条件出发(列出理由),推断出结论的证明方法,叫综合法.综合法是最常用的证明方法.
故事分析
根据李老汉的证明,你能断定玉米是老张偷的吗?你觉得有疑点吗?
李老汉想证明什么?
他是怎么证明的?
片段2:县官一时拿不定主意,就问旁边
的县丞道:“师爷,你怎么看?”
县丞说“这事要证明是老张干的,还
得弄清那袋子里装的是不是刚捌的玉米,
还要看看地里的脚印是不是老张的才行.
如果袋子里装的是刚捌的玉米,且地里的脚印是老张的,那就一定是他偷的.”
从结论出发,逆着寻找所需要的条件的思考过程,叫分析.
在分析的过程中,如果发现所需要的条件都已具备,或可从已知条件中推得,那么判断就很容易了.
讨论:我们如何判断一个命题的真假?
要判断一个命题是真命题需要推理论证;要判断一个命题是假命题只要举出一个反例即可.
例如:相等的两个角是对顶角.
1
2
反例:符合命题条件,但不符合命题结论的例子.
例3 写出下列命题的逆命题,并判断所得的逆命题是真命题还是假命题,如果是假命题,请举一个反例.
(1)内错角相等,两直线平行;
(2)如果 a = 0,那么 ab = 0.
解 : (1)逆命题:两直线平行,内错角相等,是真命题.
(2)逆命题:如果 ab = 0,那么 a = 0,是假命题.
反例:当 a = 1,b = 0 时,ab = 0.
分析:要证明 AB,CD 平行,可以找同位角相等的条件,图中∠1 与∠3 就是同位角.
我们只要找出能说明它俩相等的条件就行了.
从图中,我们可以发现∠2 与∠3 是对顶角,所以∠3 = ∠2. 又已知∠1 = ∠2,这样我们就找到了∠1 =∠3 的确切条件了.
例4 如图,∠1 =∠2,试说明直线 AB,CD 平行.
证明:因为∠2 与∠3 是对顶角,
所以∠2 = ∠3.
又因为∠1 = ∠2,
所以∠1 = ∠3,
且∠1 与∠3 是同位角.
所以 AB 与 CD 平行.
证明:
∵∠2 与∠3 是对顶角,
∴∠3 =∠2.
又∵∠1 =∠2,
∴∠1 =∠3.
∴ AB∥CD.
例5 如图,∠1 =∠2,试说明直线 AB,CD 平行.
1.下列语句中,不是命题的是( )
A. 两点之间线段最短 B. 对顶角相等
C. 不是对顶角不相等
D. 过直线 AB 外一点 P 作直线 AB 的垂线
D
2.下列命题中,是真命题的是( )
A. 若 a · b>0,则 a>0,b>0
B. 若 a · b<0,则 a<0,b<0
C. 若 a · b=0,则 a=0 且 b=0
D. 若 a · b=0,则 a=0 或 b=0
D
3. 下列句子哪些是命题?是命题的,指出是真命题还是假命题?
1) 猪有四只脚;
2) 内错角相等;
3) 画一条直线;
4) 四边形是正方形;
是
真命题
否
是
假命题
是
假命题
5) 你的作业做完了吗?
6) 内错角相等,两直线平行;
7) 同垂直于一直线的两直线平行;
8) 过点 P 画线段 MN 的垂线;
9) x>2.
否
是
真命题
是
假命题
否
否
4. 举反例说明下列命题是假命题.
(1) 若两个角不是对顶角,则这两个角不相等;
(2) 若 ab=0,则 a+b=0.
解:(1) 两条直线平行形成的内错角,这两个角不
是对顶角,但是它们相等.
(2) 当 a=5,b=0 时,ab=0,但 a+b ≠ 0.
真命题
假命题
公理
定理
(只需举一个反例)
(不需证明)
(由推理证实)
1.命题的定义:
2.命题的组成:
3.命题的分类:
判断一件事情的句子
题设和结论
小华与小刚正在津津有味地阅读《我们爱科学》.
这个黑客终于被逮住了.
是的,现在的因特网广泛运用于我们的生活中,给我们带来了方便,但……
这个黑客是个小偷.
是个喜欢穿黑衣服的贼.
坐在旁边的两个人一边听着他们的谈话,一边也在悄悄地议论着.
小明的百米成绩有进步,已达到9秒9.
好!继续努力,争取超过10秒.
不要再抢啦!每人发一个球!
有一位田径教练向领导汇报训练成绩:
相传,阎锡山在观看士兵篮球赛时,双方争抢非常激烈,于是命令:
2. 如果一个句子没有对某一件事情作出任何判断,那 么它就不是命题.
如:画线段 AB = CD.
1. 只要对一件事情作出了判断,不管正确与否,都是命题.
如:相等的角是对顶角.
注意:
像这样,对某一件事件作出正确或不正确判断的语句(或式子)叫做命题.
一、命题的概念
命题的定义与结构
例1 判断下列四个语句中,哪个是命题, 哪个不是命题?并说明理由:
(1)对顶角相等吗?
(2)画一条线段 AB = 2cm;
(3)两条直线平行,同位角相等;
(4)相等的两个角,一定是对顶角.
典例精析
解:(3)(4)是命题,(1)(2)不是命题.
理由如下:(1)是问句,故不是命题;(2)是做一件事情,也不是命题.
2)两条直线相交,有且只有一个交点( )
5)取线段 AB 的中点 C ( )
1)长度相等的两条线段是相等的线段吗?( )
6)画两条相等的线段( )
练一练:判断下列语句是不是命题?是用“√”,
不是用“× 表示.
3)不相等的两个角不是对顶角( )
4)相等的两个角是对顶角( )
×
√
×
×
√
√
观察下列命题,你能发现这些命题有什么共同的结构特
征?与同伴交流.
(1)如果两个三角形的三条边相等,那么这两个三角形的周长相等;
(2)如果两个数的绝对值相等,那么这两个数也相等;
(3)如果一个数的平方等于 9,那么这个数是 3.
都是“如果……那么……”的形式
二、命题的结构
命题一般都可以写成“如果 p,那么 q”的形式.
1. 其中 p 是这个命题的条件(题设),
2. q 是这个命题的结论(题断).
如命题:熊猫没有翅膀.改写为:
如果这个动物是熊猫,那么它就没有翅膀.
注意:添加“如果”“那么”后,命题的意义不能改变,改写的句子要完整,语句要通顺,使命题的题设和结论更明朗,易于分辨,改写过程中,要适当增加词语,切不可生搬硬套.
命题
条件
结论
已知事项
由已知事项推出的事项
两直线平行 同位角相等
题设(条件)
结论
命题的组成:
总结归纳
例2 指出下列命题的条件与结论.
(1) 两条直线都平行于同一条直线,这两条直线平行;
(2) 如果∠A =∠B,那么∠A 的补角与∠B 的补角相等.
解 : (1)“两条直线都平行于同一条直线”是条件,“两条直线平行”是结论.
(2)“∠A =∠B”是条件,“∠A 的补角与∠B 的补角相等”是结论.
把下列命题改写成“如果……那么……”的形式.并指出它的条件和结论.
1. 对顶角相等; 2. 内错角相等;
3. 两直线被第三条直线所截,同位角相等;
4. 同平行于一直线的两直线平行; 5. 等角的补角相等.
练一练
解:(1) 如果有两个角是对顶角,那么这两个角相等.
条件:有两个角是对顶角,结论:这两个角相等.
(2) 如果有两个角是内错角,那么这两个角相等.
条件:有两个角是内错角,结论:这两个角相等.
(3) 如果有两直线被第三条直线所截形成三线八角,
那么其同位角相等;
条件:有两直线被第三条直线所截形成三线八角,
结论:其同位角相等.
(4) 如果有两直线平行于同一直线,那么这两直线平行.
条件:有两直线平行于同一直线,
结论:这这两直线平行.
(5) 如果有两个角是相等,那么这两角的补角也相等.
条件:有两个角是相等,结论:这两角的补角也相等.
特别规定:
正确的命题叫真命题,错误的命题叫假命题.
命题1:“如果一个数能被 4 整除,那么它也能被 2 整除”
观察下列命题,你能发现这些命题有什么不同的特点吗?
命题 1 是一个正确的命题;命题 2 是一个错误的命题.
命题2:“如果两个角互补,那么它们是邻补角”
真命题与假命题
(1)同旁内角互补( )
(4)两点可以确定一条直线( )
(2)一个角的补角大于这个角( )
判断下列命题的真假.真的用“√”,假的用“×”表示.
(5)两点之间线段最短( )
(3)相等的两个角是对顶角( )
×
(6)同角的余角相等( )
×
√
√
√
×
练一练
做一做:指出下列命题的条件和结论,并改写成“如果 p,那么 q”的形式:
命题 条件(如果 p) 结论(那么 q)
①能被 2 整除的数是偶数
②有公共顶点的两个角是对顶角
这个数是偶数
一个数能被 2 整除
这两个角是对顶角
两个角有公共顶点
逆命题
命题 条件(如果 p) 结论(那么 q)
③两直线平行,同位角相等
④同位角相等,两直线平行
直线所截的同位角相等
两条平行线被第三条直线所截
这两条直线平行
如果两条直线被第三条直线所截的同位角相等
上述命题 ③ 与 ④ 的条件与结论之间有什么联系?
③两直线平行,同位角相等.
④同位角相等,两直线平行.
命题③与④的条件与结论互换了位置.
将命题“如果 p,那么 q”中的结论和条件互换,便得到一个新命题“如果 p,那么 q”,我们把这样的两个命题称为互逆命题,其中一个叫做原命题,另一个叫做原命题的逆命题.
例如,上述命题 ③ 与 ④ 就是互逆命题.
从上我们可以看出,只要将一个命题的条件和结论互换,就可得到它的逆命题,所以每个命题都有逆命题.
你还能举出其它的例子吗?
写出下列命题的逆命题:
(1)若两数相等,则它们的绝对值也相等;
(2)如果 m 是整数,那么它也是有理数;
(3)两直线平行,内错角相等;
(4)两边相等的三角形是等腰三角形.
绝对值相等的两个数相等.
如果 m 是有理数,那么它也是整数.
内错角相等,两直线平行.
等腰三角形的两边相等.
练一练
写出下列命题的逆命题,并判断它们的真假.
(1)如果 a = b,则 a2 = b2;
(2)等角的余角相等;
(3)同位角相等,两直线平行.
(1)如果 a2 = b2 ,则 a = b,假命题.
(2)如果两个角的余角相等,那么这两个角也相等, 真命题.
(3)两直线平行,同位角相等,真命题.
思考:原命题是真命题,那么它的逆命题也是真命题吗?
解:
反例
“因为早上我发现老张从玉米地那边过来,把一袋东西背回家,还发现我地里的玉米被人捌了,我知道老张家没有种玉米.所以我家玉米肯定是老张捌的.”
片段1:一天早上,李老汉来到衙门里告状说:老张刚刚在他地里偷捌(同扒)了一袋子玉米.吕县令立即派衙役将老张拘捕到县衙审讯:
吕县令问李老汉:“你怎知是老张偷了你的玉米 ”
这种从已知条件出发(列出理由),推断出结论的证明方法,叫综合法.综合法是最常用的证明方法.
故事分析
根据李老汉的证明,你能断定玉米是老张偷的吗?你觉得有疑点吗?
李老汉想证明什么?
他是怎么证明的?
片段2:县官一时拿不定主意,就问旁边
的县丞道:“师爷,你怎么看?”
县丞说“这事要证明是老张干的,还
得弄清那袋子里装的是不是刚捌的玉米,
还要看看地里的脚印是不是老张的才行.
如果袋子里装的是刚捌的玉米,且地里的脚印是老张的,那就一定是他偷的.”
从结论出发,逆着寻找所需要的条件的思考过程,叫分析.
在分析的过程中,如果发现所需要的条件都已具备,或可从已知条件中推得,那么判断就很容易了.
讨论:我们如何判断一个命题的真假?
要判断一个命题是真命题需要推理论证;要判断一个命题是假命题只要举出一个反例即可.
例如:相等的两个角是对顶角.
1
2
反例:符合命题条件,但不符合命题结论的例子.
例3 写出下列命题的逆命题,并判断所得的逆命题是真命题还是假命题,如果是假命题,请举一个反例.
(1)内错角相等,两直线平行;
(2)如果 a = 0,那么 ab = 0.
解 : (1)逆命题:两直线平行,内错角相等,是真命题.
(2)逆命题:如果 ab = 0,那么 a = 0,是假命题.
反例:当 a = 1,b = 0 时,ab = 0.
分析:要证明 AB,CD 平行,可以找同位角相等的条件,图中∠1 与∠3 就是同位角.
我们只要找出能说明它俩相等的条件就行了.
从图中,我们可以发现∠2 与∠3 是对顶角,所以∠3 = ∠2. 又已知∠1 = ∠2,这样我们就找到了∠1 =∠3 的确切条件了.
例4 如图,∠1 =∠2,试说明直线 AB,CD 平行.
证明:因为∠2 与∠3 是对顶角,
所以∠2 = ∠3.
又因为∠1 = ∠2,
所以∠1 = ∠3,
且∠1 与∠3 是同位角.
所以 AB 与 CD 平行.
证明:
∵∠2 与∠3 是对顶角,
∴∠3 =∠2.
又∵∠1 =∠2,
∴∠1 =∠3.
∴ AB∥CD.
例5 如图,∠1 =∠2,试说明直线 AB,CD 平行.
1.下列语句中,不是命题的是( )
A. 两点之间线段最短 B. 对顶角相等
C. 不是对顶角不相等
D. 过直线 AB 外一点 P 作直线 AB 的垂线
D
2.下列命题中,是真命题的是( )
A. 若 a · b>0,则 a>0,b>0
B. 若 a · b<0,则 a<0,b<0
C. 若 a · b=0,则 a=0 且 b=0
D. 若 a · b=0,则 a=0 或 b=0
D
3. 下列句子哪些是命题?是命题的,指出是真命题还是假命题?
1) 猪有四只脚;
2) 内错角相等;
3) 画一条直线;
4) 四边形是正方形;
是
真命题
否
是
假命题
是
假命题
5) 你的作业做完了吗?
6) 内错角相等,两直线平行;
7) 同垂直于一直线的两直线平行;
8) 过点 P 画线段 MN 的垂线;
9) x>2.
否
是
真命题
是
假命题
否
否
4. 举反例说明下列命题是假命题.
(1) 若两个角不是对顶角,则这两个角不相等;
(2) 若 ab=0,则 a+b=0.
解:(1) 两条直线平行形成的内错角,这两个角不
是对顶角,但是它们相等.
(2) 当 a=5,b=0 时,ab=0,但 a+b ≠ 0.
真命题
假命题
公理
定理
(只需举一个反例)
(不需证明)
(由推理证实)
1.命题的定义:
2.命题的组成:
3.命题的分类:
判断一件事情的句子
题设和结论
