12.4 综合与实践一次函数模型的应用(1)课件(共74张PPT)
文档属性
| 名称 | 12.4 综合与实践一次函数模型的应用(1)课件(共74张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-07 00:00:00 | ||
图片预览











文档简介
(共74张PPT)
逐点
导讲练
课堂小结
作业提升
课时讲解
1
课时流程
2
一次函数模型的应用
选择方案
知1-讲
知识点
一次函数模型的应用
1
1. 利用函数解决实际问题的基本模式
知1-讲
特别解读
1. 若题目中明确给出两变量的函数关系,则可用待定系数法求出函数表达式 .
2. 若题目中明确给出两变量变化关系的图象,则由图象分辨出其函数类型,进而用待定系数法求出函数表达式 .
2. 建立函数模型的一般步骤
(1) 获取数据; (2)列表、描点; (3)观察、猜想;
(4)求出函数表达式; (5)检验并给出答案 .
知1-讲
知1-练
为提醒人们节约用水,及时修好漏水的水龙头, 小王做了一个水龙头漏水实验,他用于接水的量筒最大容量为100 毫升 .
下表是小王同学在做实验时,每隔 10 秒观察量筒中水的体积记录下的数据(漏出的水量精确到 1 毫升):
例1
时间 t/ 秒 10 20 30 40 50 60 70
漏出的水量
V/ 毫升 2 5 8 11 14 17 20
知1-练
解题秘方:紧扣建立函数模型的一般步骤,建立一次函数模型解决问题 .
知1-练
解:描点,如图 12.4-1 所示 .
(1)在平面直角坐标系中描出上表中数据对应的点;
知1-练
(2)如果小王同学继续做实验,试探求多少秒后量筒中的水会满而溢出(精确到 1 秒);
知1-练
解:由图 12.4-1 知 V 与 t 之间是一次函数的 关系 ,
设 V=kt+b(k ≠ 0),
根据表中数据知 ,
当 t=10 时, V=2;当 t=20 时,V=5.
知1-练
技巧点拨
观察图象可知所描各点大致在一条直线上,因此可认为两变量之间存在一次函数关系 . 注意借助其中两点的坐标求出函数表达式后需利用其余各点的坐标进行验证 .
知1-练
知1-练
(3)按此漏水速度, 1小时会漏水多少升(精确到0.1升)?
知1-练
小明练习 100 m 短跑,训练时间与短跑成绩记录如下:
例2
时间 x / 月 1 2 3 4
成绩 y /s 15.6 15.4 15.2 15
知1-练
解题秘方:根据表中的数据建立一次函数模型,再利用一次函数对数据作预测 .
知1-练
方法点拨
根据给定部分因变量随自变量均匀变化的数据信息,可以建立一次函数模型,利用求得的一次函数表达式,可以对数据的邻近区域进行预测 . 但是预测只能在数据的邻近区域,远离已知数据作预测是不可靠的 .
知1-练
(1)请你为小明的 100 m 短跑成绩 y (s)与训练时间x (月)的关系建立函数模型;
知1-练
解:当 x=6 时, y=-0.2×6 +15.8=14.6.
故预测小明训练 6 个月的 100 m 短跑成绩为 14.6 s.
(2)用所求出的函数表达式预测小明训练 6 个月的 100 m短跑成绩;
知1-练
解:不能 . 理由:因为短跑的成绩在短时间内可能呈某种趋势,但在较长的时间内,受自身的发展极限的限制,不会永远如此快地提高 .(理由合理即可)
(3)能用所求出的函数表达式预测小明训练 3 年的 100 m短跑成绩吗?为什么?
知2-讲
知识点
选择方案
2
1.选择方案
选择方案是指某一问题中,符合条件的方案有多种,一般要利用数学知识经过分析、猜想、判断,筛选出最佳方案,涉及的问题类型常有利润最大、路程最短、运费最少、效率最高等,需要建立函数模型,运用方程(组)或不等式的知识进行求解 .
知2-讲
特别提醒
◆解决含多个变量的问题时,注意分析这些变量之间的关系,从中选取一个能影响其他变量的变量作为自变量,然后根据已知的条件寻求可以反映实际问题的函数,以此作为解决问题的数学模型 .
◆选择最佳方案实 际上是在比较的基础上完成的,它往往是将全部方案一一列举出来,然后根据题意选择一个最优的方案 .
知2-讲
2. 用一次函数选择方案的一般步骤
(1) “析”: 分析题意,弄清数量关系 .
(2)“列”: 列出函数表达式、不等式或方程 (组).
(3)“求”: 求出自变量取不同值时对应的函数值的大小,或函数的最大(最小)值 .
(4)“选”: 结合实际需要选择最佳方案 .
注意: 在选择方案时,要考虑实际问题中自变量的取值范围,尤其要看它是不是某些特殊解(如正整数解) .
知2-练
例3
[ 中考·襄阳 ]某社区活动中心为鼓励居民加强体育锻炼,准备购买 10 副某种品牌的羽毛球拍,每副球拍配 x ( x ≥ 2 )个羽毛球,供社区居民免费借用 . 该社区附近 A, B 两家超市都有这种品牌的羽毛球拍和羽毛球出售,每副球拍的标价均为 30 元,每个羽毛球的标价均为 3 元,目前两家超市都在做促销活动:
知2-练
A 超市:所有商品均打九折(按标价的 90% )销售;
B 超市:买1副羽毛球拍送 2 个羽毛球 .
设在 A 超市购买羽毛球拍和羽毛球的费用为 yA 元,在 B超市购买羽毛球拍和羽毛球的费用为 yB 元 . 请解答下列问题:
知2-练
解题秘方:紧扣标价与折扣间的数量关系建立一次函数模型,用方程、不等式进行分类讨论 .
知2-练
(1)分别写出 yA 和 yB 与 x 之间的函数表达式 .
解:由题意得
yA = ( 10×30+10×3 x ) ×0.9=27 x +270 ( x ≥ 2 ) , yB =10×30+10×3 ( x - 2 ) =30 x +240 ( x ≥ 2 ) .
知2-练
(2)若该活动中心只在一家超市购买,你认为在哪家超市购买更划算?
解:当 yA = yB 时,27 x +270=30 x +240,得 x =10;
当 yA > yB时,27 x +270>30 x +240,得 x <10;
当 yA < yB 时,27 x +270<30 x +240,得 x >10.
∴当 2 ≤ x <10 时,在 B 超市购买更划算;
当 x =10 时,在两家超市购买费用一样;
当 x >10 时,在 A 超市购买更划算 .
知2-练
(3)若每副球拍配 15 个羽毛球,请你帮助该活动中心设计出最省钱的购买方案 .
解:由题意,若“只在一家超市购买”,由于 x =15>10,则到 A 超市购买较省钱,此时
yA =27 x+270=27×15+270=675.
知2-练
注意本问中没有限制条件“只在一家超市购买”,因此先在 B 超市购买 10 副羽毛球拍,送 20 个羽毛球,然后在 A 超市购买剩下的羽毛球,需
( 10×15 - 20 ) ×3×0.9=351 (元) ,共需费用 10×30+351=651 (元) .
知2-练
因为651<675,所以最省钱的方案是先在 B 超市购买 10 副羽毛球拍,送 20 个羽毛球,然后在 A 超市购买 130 个羽毛球 .
思路点拨
方案最优问题,往往是将所有的方案一一列举,作出比较 . 本题选出花费最少的方案为最优方案 .
知2-练
技巧点拨
解一次函数与方程、不等式综合的实际应用问题的方法:
先读懂题意,理解题干的条件和各个问题的关系,并利用题目中的信息建立函数模型,根据函数值的大小关系,建立方程、不等式模型;
再分类讨论,确定不同情况下自变量的取值范围及对应的函数值范围,从而得出不同范围内的方案 .
本例的解答运用了分类讨论思想,解答的关键是建立函数模型 .
知2-练
[ 三模·温州 ] 某工厂一天使用甲、乙两台机器生产某种零件,甲机器生产完 5 000 个零件后发生了故障,修理了2 小时,继续工作 . 如图 12.4﹣2 表示甲、乙两台机器的产量与时间的关系,已知乙机器在甲机器刚维修完后的产量恰好比甲机器的产量多 1 000 个 .
例4
知2-练
解题秘方: (1)由题知甲机器生产 5 000 个后维修,可得 m 的值,由点 E 的坐标可得乙机器的生产效率;
知2-练
解:m = 5 000,
乙机器的生产效率为 1 000 个 / 时 .
(1)请直接写出 m 的值和乙机器的生产效率;
知2-练
解题秘方: (2)根据图象得出在 b 小时时乙机器的产量比甲机器多1 000 个,列方程求解可得 b 的值,由甲机器修理了 2 小时可得 a 的值;
知2-练
解:由题知在 b 小时时乙机器的产量比甲机器多
1 000 个,
所以有 1 000b - 5 000 = 1 000,解得 b = 6.
所以 a=b - 2=4.所以 a = 4, b = 6.
(2)求出 a 和 b 的值;
知2-练
解题秘方: (3)可得甲机器修理前的生产效率为 5 000÷4=1 250(个 / 时),根据题意列式表示甲、乙两台机器的产量,令t - 6 = x,1 - n% = y,根据 n, t 的取值范围得 x ≤ 9,0.9 <y < 1, x, t, n 都为正整数,可得 5xy - 4x = 4,则 x 为 5,6,7,再分类讨论即可得.
知2-练
(3)已知甲机器修理后生产效率降低 n%( n 是小于 10 的正整数),当甲总产量追上乙时,所用的时间 t(小时)恰好是整数,若机器一天内工作不得超过 15 小时(包括维修时间),请求出正整数 n 的值.
知2-练
解:由题易得,甲机器修理后的生产效率为
1 250 (1 - n%)个 / 时, 当甲追上乙时,( t - 6)×1 250(1 - n %)+5 000=1 000t( n < 10),且 t ≤ 15,
令 t - 6=x,所以 x ≤ 9.
令 1 - n % = y, 所以 0.9 < y < 1,
所以 1 250xy+5 000 =1 000(6+x),所以 5xy - 4x = 4,
知2-练
知2-练
某县大力发展猕猴桃产业,预计今年 A 地将采摘200 吨, B 地将采摘 300 吨 . 若要将这些猕猴桃运到甲、乙两个仓库,已知甲仓库可储存 240 吨,乙仓库可储存 260 吨,从A 地运往甲、乙两仓库的费用分别为每吨 20 元和 25 元,从 B地运往甲、乙两仓库的费用分别为每吨 15 元和 18 元 . 设从 A地运往甲仓库的猕猴桃为 x 吨, A, B 两地运往两仓库的猕猴桃费用分别为 yA 元和 yB 元 .
例5
知2-练
解法提醒
当调运方案中涉及两个函数表达式时,要比较费用的大小,一般要分三种情况利用不等式或方程分类讨论求解;而要求得最省钱的调运方案时,一般先根据数量之间的关系建立函数,然后利用一次函数的增减性确定出符合要求的最佳方案 .
知2-练
解题秘方:紧扣“调运过程中费用间的关系”列出一次函数表达式,用比较法求解 .
知2-练
解:由题意得,从 A 地运往乙仓库的猕猴桃为(200 - x)吨,从 B 地运往甲仓库的猕猴桃为(240 - x)吨,从 B 地运往乙仓库的猕猴桃为(60+x)吨 .
则 yA=20x+25(200 - x)=-5x+5 000,
yB=15(240 - x)+18(60+x)=3x+4 680.
(1)分别求出 yA, yB 与 x 之间的函数表达式;
知2-练
技巧点拨
求解调运方案问题,常借助表格来分析问题,如本题,调运情况如下表.
甲 乙 总计
A x 200- x 200
B 240- x 60+x 300
总计 240 260 500
知2-练
解:因为 yA - yB= ( - 5x+5 000 ) - ( 3x+4 680 ) =
- 8x+320,所以当 - 8x+320 > 0,即 x < 40 时, B 地的运费较少;
当 - 8x+320=0,即 x=40 时,两地的运费一样多;
当 - 8x+320 < 0,即 x > 40 时, A 地的运费较少 .
(2)试讨论 A, B 两地的运费哪个较少;
知2-练
(3)考虑 B 地的经济承受能力, B 地的猕猴桃运费不得超过 4 830 元,在这种情况下,请问怎样调运才能使两地运费之和最少?求出最少运费 .
知2-练
解:设两地运费之和为 W 元,
则 W=yA+yB=( - 5x+5 000)+(3x+4 680)=
- 2x+9 680,由3x+4 680 ≤ 4 830,解得 x ≤ 50,所以 W 的最小值为 - 2×50+9 680=9 580.故当 A 地运往甲、乙两仓库的猕猴桃分别为 50吨、150吨, B 地运往甲、乙两仓库的猕猴桃分别为 190吨、110吨时,才能使两地运费之和最少,最少运费是 9 580 元 .
知2-练
特别警示
由 W= - 2x+9 680可知, W 随 x 的增大而减小,切忌忽略第(3)问对x取值范围的限制,认为 x=200 时满足题意 .
知2-练
某公司推销文化衫,设 x(件)是推销产品的数量,y(元)是付给推销员的推销费,如图 12.4﹣3 表示公司每月付给推销员的推销费的两种方案,根据图象解答下列问题 .
例6
知2-练
解题秘方:从图象中获取求函数表达式的信息并通过图象信息选择支付方案 .
知2-练
解:设这两个函数的表达式分别为 y1=k1x( k1 ≠ 0), y2=k2x+b( k2 ≠ 0).
由 y1 关于 x 的函数图象经过点(30,600),得 600=30k1,解得 k1=20,所以y1 关于 x 的函数表达式为 y1=20x( x ≥ 0).
由 y2 关于 x 的函数图象经过点(0,300), 点(30,600), 得 b=300,600=30k2+b, 解得k2=10,所以 y2 关于 x 的函数表达式为 y2=10x+300( x ≥ 0).
(1)分别求 y1, y2 关于 x 的函数表达式;
知2-练
解:y1 的付费方案是不推销产品没有推销费,每推销 1
件产品得推销费 20 元; y2 的付费方案是保底工资 300 元,另外每推销 1 件产品再得推销费 10 元 .
(2)解释图中表示的两种方案是如何付推销费的;
知2-练
解:①当平均每月推销产品的数量等于 30 件时,两种方案都可以 . ②当平均每月推销产品的数量多于 30 件时,选择 y1 的付费方案;③当平均每月推销产品的数量少于 30 件时,选择 y2 的付费方案 .
(3)如果你是推销员,应如何选择付费方案?
知2-练
思路点拨
(1)由待定系数法结合特殊点求解即可;
(2)根据两直线与 y轴的交点,结合实际进行分析;
(3)根据业务能力,结合(2) 中两种方案的付费方式进行解答 .
知2-练
某商店销售 10 台 A 型电脑和 20 台 B 型电脑的利润为 4 000 元,销售 20 台 A 型电脑和 10 台 B 型电脑的利润为3 500 元 .
例7
知2-练
解法提醒
在商品经营活动中,经常会遇到求最大利润、最大销量等问题,解此类问题的关键是通过题意,确定出函数的表达式,然后根据函数的增减性确定其最大值,且要注意自变量的取值范围和问题的实际意义 .
知2-练
解题秘方:从列方程组求方程组解中获取求一次函数关系式的数据,并根据一次函数的性质求方案 .
知2-练
(1)求每台 A 型电脑和 B 型电脑的销售利润;
知2-练
详解
根据“销售10台A型电脑和20台B型电脑的利润为4 000元”可得10a+20b=4 000;根据“销售20台A型电脑和10台B型电脑的利润为3 500元”可20a+10b=3 500.
知2-练
(2)该商店计划一次购进两种型号的电脑共 100 台,其中 B 型电脑的进货量不超过 A 型电脑的 2 倍 . 设购进 A 型电脑 x 台,这 100 台电脑的销售总利润为 y 元 .
① 求 y 关于 x 的函数关系式;
解:根据题意得 y=100x+150 ( 100 - x ) ,
即 y= - 50x+15 000.
知2-练
② 该商店购进 A 型电脑、 B 型电脑各多少台,才能使销售总利润最大?
知2-练
③ 实际进货时,厂家对 A 型电脑出厂价下调 m(0知2-练
特别警示
本题③中,容易忽视一次函数随 m 值变化,其增减性也发生变化,不会利用分类讨论求解而产生错误 .
知2-练
知2-练
详解
y=(100+m)x+150·(100-x)
=(100+m)x+15 000-150x
=(100+m-150)x+15 000
=(m-50)x+15 000.
知2-练
知2-练
[ 中考·郴州 ] 某工厂有甲种原料 130 kg,乙种原料
144 kg,现用这两种原料生产出 A, B 两种产品共 30 件,已知生产每件 A 产品需甲种原料 5 kg,乙种原料 4 kg,且每件A 产品可获利 700 元;生产每件 B 产品需甲种原料 3 kg,乙种原料 6 kg, 且每件 B 产品可获利 900 元,设生产 A 产品 x 件(产品件数为整数),根据以上信息解答下列问题:
例8
知2-练
解题秘方:从列不等式组求其解集中获取数据确定方案;由函数的增减性确定利润最大的方案 .
知2-练
(1)生产 A, B 两种产品的方案有哪几种?
知2-练
因为产品件数为整数,所以 x 取整数解 .
所以 x=18 或 x=19 或 x=20.
所以生产 A, B 两种产品的方案有如下三种:
方案一: A 产品 18 件, B 产品 12 件;
方案二: A 产品 19 件, B 产品 11 件;
方案三: A 产品 20 件, B 产品 10 件 .
知2-练
(2)设生产这 30 件产品可获利 y 元,写出 y 关于 x 的函数表达式,写出(1)中利润最大的方案,并求出最大利润 .
知2-练
解:由题意可得 y=700x+900(30-x)=-200x+27 000,因为 -200<0,所以 y 随 x 的增大而减小,
又因为 18 ≤ x ≤ 20,所以当 x=18 时有最大利润,
此时 y =-200×18+27 000=23 400.
答: (1)中利润最大的方案是方案一,即生产 A 产品 18 件,B 产品 12 件,最大利润为 23 400 元 .
知2-练
解法提醒
利用方程(组)、不等式(组)求解方案类问题的策略:
求解方案类问题时,应先正确建立函数模型,确定自变量的取值范围, 然后可利用函数的性质求最大(小)值; 或计算出各种方案的值进行大小比较,注意自变量的整数取值问题 .
综合与实践
一次函数模型的应用
用一次函数
解决问题
用函数图象解决问题
用函数性质解决问题
逐点
导讲练
课堂小结
作业提升
课时讲解
1
课时流程
2
一次函数模型的应用
选择方案
知1-讲
知识点
一次函数模型的应用
1
1. 利用函数解决实际问题的基本模式
知1-讲
特别解读
1. 若题目中明确给出两变量的函数关系,则可用待定系数法求出函数表达式 .
2. 若题目中明确给出两变量变化关系的图象,则由图象分辨出其函数类型,进而用待定系数法求出函数表达式 .
2. 建立函数模型的一般步骤
(1) 获取数据; (2)列表、描点; (3)观察、猜想;
(4)求出函数表达式; (5)检验并给出答案 .
知1-讲
知1-练
为提醒人们节约用水,及时修好漏水的水龙头, 小王做了一个水龙头漏水实验,他用于接水的量筒最大容量为100 毫升 .
下表是小王同学在做实验时,每隔 10 秒观察量筒中水的体积记录下的数据(漏出的水量精确到 1 毫升):
例1
时间 t/ 秒 10 20 30 40 50 60 70
漏出的水量
V/ 毫升 2 5 8 11 14 17 20
知1-练
解题秘方:紧扣建立函数模型的一般步骤,建立一次函数模型解决问题 .
知1-练
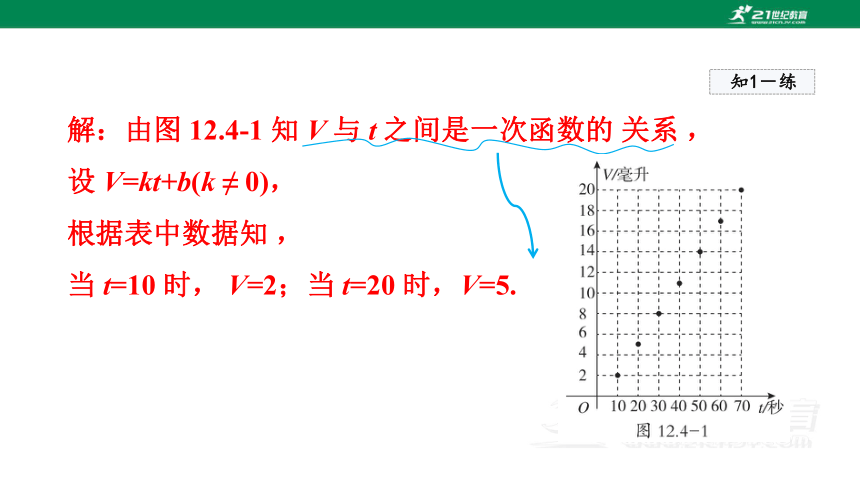
解:描点,如图 12.4-1 所示 .
(1)在平面直角坐标系中描出上表中数据对应的点;
知1-练
(2)如果小王同学继续做实验,试探求多少秒后量筒中的水会满而溢出(精确到 1 秒);
知1-练
解:由图 12.4-1 知 V 与 t 之间是一次函数的 关系 ,
设 V=kt+b(k ≠ 0),
根据表中数据知 ,
当 t=10 时, V=2;当 t=20 时,V=5.
知1-练
技巧点拨
观察图象可知所描各点大致在一条直线上,因此可认为两变量之间存在一次函数关系 . 注意借助其中两点的坐标求出函数表达式后需利用其余各点的坐标进行验证 .
知1-练
知1-练
(3)按此漏水速度, 1小时会漏水多少升(精确到0.1升)?
知1-练
小明练习 100 m 短跑,训练时间与短跑成绩记录如下:
例2
时间 x / 月 1 2 3 4
成绩 y /s 15.6 15.4 15.2 15
知1-练
解题秘方:根据表中的数据建立一次函数模型,再利用一次函数对数据作预测 .
知1-练
方法点拨
根据给定部分因变量随自变量均匀变化的数据信息,可以建立一次函数模型,利用求得的一次函数表达式,可以对数据的邻近区域进行预测 . 但是预测只能在数据的邻近区域,远离已知数据作预测是不可靠的 .
知1-练
(1)请你为小明的 100 m 短跑成绩 y (s)与训练时间x (月)的关系建立函数模型;
知1-练
解:当 x=6 时, y=-0.2×6 +15.8=14.6.
故预测小明训练 6 个月的 100 m 短跑成绩为 14.6 s.
(2)用所求出的函数表达式预测小明训练 6 个月的 100 m短跑成绩;
知1-练
解:不能 . 理由:因为短跑的成绩在短时间内可能呈某种趋势,但在较长的时间内,受自身的发展极限的限制,不会永远如此快地提高 .(理由合理即可)
(3)能用所求出的函数表达式预测小明训练 3 年的 100 m短跑成绩吗?为什么?
知2-讲
知识点
选择方案
2
1.选择方案
选择方案是指某一问题中,符合条件的方案有多种,一般要利用数学知识经过分析、猜想、判断,筛选出最佳方案,涉及的问题类型常有利润最大、路程最短、运费最少、效率最高等,需要建立函数模型,运用方程(组)或不等式的知识进行求解 .
知2-讲
特别提醒
◆解决含多个变量的问题时,注意分析这些变量之间的关系,从中选取一个能影响其他变量的变量作为自变量,然后根据已知的条件寻求可以反映实际问题的函数,以此作为解决问题的数学模型 .
◆选择最佳方案实 际上是在比较的基础上完成的,它往往是将全部方案一一列举出来,然后根据题意选择一个最优的方案 .
知2-讲
2. 用一次函数选择方案的一般步骤
(1) “析”: 分析题意,弄清数量关系 .
(2)“列”: 列出函数表达式、不等式或方程 (组).
(3)“求”: 求出自变量取不同值时对应的函数值的大小,或函数的最大(最小)值 .
(4)“选”: 结合实际需要选择最佳方案 .
注意: 在选择方案时,要考虑实际问题中自变量的取值范围,尤其要看它是不是某些特殊解(如正整数解) .
知2-练
例3
[ 中考·襄阳 ]某社区活动中心为鼓励居民加强体育锻炼,准备购买 10 副某种品牌的羽毛球拍,每副球拍配 x ( x ≥ 2 )个羽毛球,供社区居民免费借用 . 该社区附近 A, B 两家超市都有这种品牌的羽毛球拍和羽毛球出售,每副球拍的标价均为 30 元,每个羽毛球的标价均为 3 元,目前两家超市都在做促销活动:
知2-练
A 超市:所有商品均打九折(按标价的 90% )销售;
B 超市:买1副羽毛球拍送 2 个羽毛球 .
设在 A 超市购买羽毛球拍和羽毛球的费用为 yA 元,在 B超市购买羽毛球拍和羽毛球的费用为 yB 元 . 请解答下列问题:
知2-练
解题秘方:紧扣标价与折扣间的数量关系建立一次函数模型,用方程、不等式进行分类讨论 .
知2-练
(1)分别写出 yA 和 yB 与 x 之间的函数表达式 .
解:由题意得
yA = ( 10×30+10×3 x ) ×0.9=27 x +270 ( x ≥ 2 ) , yB =10×30+10×3 ( x - 2 ) =30 x +240 ( x ≥ 2 ) .
知2-练
(2)若该活动中心只在一家超市购买,你认为在哪家超市购买更划算?
解:当 yA = yB 时,27 x +270=30 x +240,得 x =10;
当 yA > yB时,27 x +270>30 x +240,得 x <10;
当 yA < yB 时,27 x +270<30 x +240,得 x >10.
∴当 2 ≤ x <10 时,在 B 超市购买更划算;
当 x =10 时,在两家超市购买费用一样;
当 x >10 时,在 A 超市购买更划算 .
知2-练
(3)若每副球拍配 15 个羽毛球,请你帮助该活动中心设计出最省钱的购买方案 .
解:由题意,若“只在一家超市购买”,由于 x =15>10,则到 A 超市购买较省钱,此时
yA =27 x+270=27×15+270=675.
知2-练
注意本问中没有限制条件“只在一家超市购买”,因此先在 B 超市购买 10 副羽毛球拍,送 20 个羽毛球,然后在 A 超市购买剩下的羽毛球,需
( 10×15 - 20 ) ×3×0.9=351 (元) ,共需费用 10×30+351=651 (元) .
知2-练
因为651<675,所以最省钱的方案是先在 B 超市购买 10 副羽毛球拍,送 20 个羽毛球,然后在 A 超市购买 130 个羽毛球 .
思路点拨
方案最优问题,往往是将所有的方案一一列举,作出比较 . 本题选出花费最少的方案为最优方案 .
知2-练
技巧点拨
解一次函数与方程、不等式综合的实际应用问题的方法:
先读懂题意,理解题干的条件和各个问题的关系,并利用题目中的信息建立函数模型,根据函数值的大小关系,建立方程、不等式模型;
再分类讨论,确定不同情况下自变量的取值范围及对应的函数值范围,从而得出不同范围内的方案 .
本例的解答运用了分类讨论思想,解答的关键是建立函数模型 .
知2-练
[ 三模·温州 ] 某工厂一天使用甲、乙两台机器生产某种零件,甲机器生产完 5 000 个零件后发生了故障,修理了2 小时,继续工作 . 如图 12.4﹣2 表示甲、乙两台机器的产量与时间的关系,已知乙机器在甲机器刚维修完后的产量恰好比甲机器的产量多 1 000 个 .
例4
知2-练
解题秘方: (1)由题知甲机器生产 5 000 个后维修,可得 m 的值,由点 E 的坐标可得乙机器的生产效率;
知2-练
解:m = 5 000,
乙机器的生产效率为 1 000 个 / 时 .
(1)请直接写出 m 的值和乙机器的生产效率;
知2-练
解题秘方: (2)根据图象得出在 b 小时时乙机器的产量比甲机器多1 000 个,列方程求解可得 b 的值,由甲机器修理了 2 小时可得 a 的值;
知2-练
解:由题知在 b 小时时乙机器的产量比甲机器多
1 000 个,
所以有 1 000b - 5 000 = 1 000,解得 b = 6.
所以 a=b - 2=4.所以 a = 4, b = 6.
(2)求出 a 和 b 的值;
知2-练
解题秘方: (3)可得甲机器修理前的生产效率为 5 000÷4=1 250(个 / 时),根据题意列式表示甲、乙两台机器的产量,令t - 6 = x,1 - n% = y,根据 n, t 的取值范围得 x ≤ 9,0.9 <y < 1, x, t, n 都为正整数,可得 5xy - 4x = 4,则 x 为 5,6,7,再分类讨论即可得.
知2-练
(3)已知甲机器修理后生产效率降低 n%( n 是小于 10 的正整数),当甲总产量追上乙时,所用的时间 t(小时)恰好是整数,若机器一天内工作不得超过 15 小时(包括维修时间),请求出正整数 n 的值.
知2-练
解:由题易得,甲机器修理后的生产效率为
1 250 (1 - n%)个 / 时, 当甲追上乙时,( t - 6)×1 250(1 - n %)+5 000=1 000t( n < 10),且 t ≤ 15,
令 t - 6=x,所以 x ≤ 9.
令 1 - n % = y, 所以 0.9 < y < 1,
所以 1 250xy+5 000 =1 000(6+x),所以 5xy - 4x = 4,
知2-练
知2-练
某县大力发展猕猴桃产业,预计今年 A 地将采摘200 吨, B 地将采摘 300 吨 . 若要将这些猕猴桃运到甲、乙两个仓库,已知甲仓库可储存 240 吨,乙仓库可储存 260 吨,从A 地运往甲、乙两仓库的费用分别为每吨 20 元和 25 元,从 B地运往甲、乙两仓库的费用分别为每吨 15 元和 18 元 . 设从 A地运往甲仓库的猕猴桃为 x 吨, A, B 两地运往两仓库的猕猴桃费用分别为 yA 元和 yB 元 .
例5
知2-练
解法提醒
当调运方案中涉及两个函数表达式时,要比较费用的大小,一般要分三种情况利用不等式或方程分类讨论求解;而要求得最省钱的调运方案时,一般先根据数量之间的关系建立函数,然后利用一次函数的增减性确定出符合要求的最佳方案 .
知2-练
解题秘方:紧扣“调运过程中费用间的关系”列出一次函数表达式,用比较法求解 .
知2-练
解:由题意得,从 A 地运往乙仓库的猕猴桃为(200 - x)吨,从 B 地运往甲仓库的猕猴桃为(240 - x)吨,从 B 地运往乙仓库的猕猴桃为(60+x)吨 .
则 yA=20x+25(200 - x)=-5x+5 000,
yB=15(240 - x)+18(60+x)=3x+4 680.
(1)分别求出 yA, yB 与 x 之间的函数表达式;
知2-练
技巧点拨
求解调运方案问题,常借助表格来分析问题,如本题,调运情况如下表.
甲 乙 总计
A x 200- x 200
B 240- x 60+x 300
总计 240 260 500
知2-练
解:因为 yA - yB= ( - 5x+5 000 ) - ( 3x+4 680 ) =
- 8x+320,所以当 - 8x+320 > 0,即 x < 40 时, B 地的运费较少;
当 - 8x+320=0,即 x=40 时,两地的运费一样多;
当 - 8x+320 < 0,即 x > 40 时, A 地的运费较少 .
(2)试讨论 A, B 两地的运费哪个较少;
知2-练
(3)考虑 B 地的经济承受能力, B 地的猕猴桃运费不得超过 4 830 元,在这种情况下,请问怎样调运才能使两地运费之和最少?求出最少运费 .
知2-练
解:设两地运费之和为 W 元,
则 W=yA+yB=( - 5x+5 000)+(3x+4 680)=
- 2x+9 680,由3x+4 680 ≤ 4 830,解得 x ≤ 50,所以 W 的最小值为 - 2×50+9 680=9 580.故当 A 地运往甲、乙两仓库的猕猴桃分别为 50吨、150吨, B 地运往甲、乙两仓库的猕猴桃分别为 190吨、110吨时,才能使两地运费之和最少,最少运费是 9 580 元 .
知2-练
特别警示
由 W= - 2x+9 680可知, W 随 x 的增大而减小,切忌忽略第(3)问对x取值范围的限制,认为 x=200 时满足题意 .
知2-练
某公司推销文化衫,设 x(件)是推销产品的数量,y(元)是付给推销员的推销费,如图 12.4﹣3 表示公司每月付给推销员的推销费的两种方案,根据图象解答下列问题 .
例6
知2-练
解题秘方:从图象中获取求函数表达式的信息并通过图象信息选择支付方案 .
知2-练
解:设这两个函数的表达式分别为 y1=k1x( k1 ≠ 0), y2=k2x+b( k2 ≠ 0).
由 y1 关于 x 的函数图象经过点(30,600),得 600=30k1,解得 k1=20,所以y1 关于 x 的函数表达式为 y1=20x( x ≥ 0).
由 y2 关于 x 的函数图象经过点(0,300), 点(30,600), 得 b=300,600=30k2+b, 解得k2=10,所以 y2 关于 x 的函数表达式为 y2=10x+300( x ≥ 0).
(1)分别求 y1, y2 关于 x 的函数表达式;
知2-练
解:y1 的付费方案是不推销产品没有推销费,每推销 1
件产品得推销费 20 元; y2 的付费方案是保底工资 300 元,另外每推销 1 件产品再得推销费 10 元 .
(2)解释图中表示的两种方案是如何付推销费的;
知2-练
解:①当平均每月推销产品的数量等于 30 件时,两种方案都可以 . ②当平均每月推销产品的数量多于 30 件时,选择 y1 的付费方案;③当平均每月推销产品的数量少于 30 件时,选择 y2 的付费方案 .
(3)如果你是推销员,应如何选择付费方案?
知2-练
思路点拨
(1)由待定系数法结合特殊点求解即可;
(2)根据两直线与 y轴的交点,结合实际进行分析;
(3)根据业务能力,结合(2) 中两种方案的付费方式进行解答 .
知2-练
某商店销售 10 台 A 型电脑和 20 台 B 型电脑的利润为 4 000 元,销售 20 台 A 型电脑和 10 台 B 型电脑的利润为3 500 元 .
例7
知2-练
解法提醒
在商品经营活动中,经常会遇到求最大利润、最大销量等问题,解此类问题的关键是通过题意,确定出函数的表达式,然后根据函数的增减性确定其最大值,且要注意自变量的取值范围和问题的实际意义 .
知2-练
解题秘方:从列方程组求方程组解中获取求一次函数关系式的数据,并根据一次函数的性质求方案 .
知2-练
(1)求每台 A 型电脑和 B 型电脑的销售利润;
知2-练
详解
根据“销售10台A型电脑和20台B型电脑的利润为4 000元”可得10a+20b=4 000;根据“销售20台A型电脑和10台B型电脑的利润为3 500元”可20a+10b=3 500.
知2-练
(2)该商店计划一次购进两种型号的电脑共 100 台,其中 B 型电脑的进货量不超过 A 型电脑的 2 倍 . 设购进 A 型电脑 x 台,这 100 台电脑的销售总利润为 y 元 .
① 求 y 关于 x 的函数关系式;
解:根据题意得 y=100x+150 ( 100 - x ) ,
即 y= - 50x+15 000.
知2-练
② 该商店购进 A 型电脑、 B 型电脑各多少台,才能使销售总利润最大?
知2-练
③ 实际进货时,厂家对 A 型电脑出厂价下调 m(0
特别警示
本题③中,容易忽视一次函数随 m 值变化,其增减性也发生变化,不会利用分类讨论求解而产生错误 .
知2-练
知2-练
详解
y=(100+m)x+150·(100-x)
=(100+m)x+15 000-150x
=(100+m-150)x+15 000
=(m-50)x+15 000.
知2-练
知2-练
[ 中考·郴州 ] 某工厂有甲种原料 130 kg,乙种原料
144 kg,现用这两种原料生产出 A, B 两种产品共 30 件,已知生产每件 A 产品需甲种原料 5 kg,乙种原料 4 kg,且每件A 产品可获利 700 元;生产每件 B 产品需甲种原料 3 kg,乙种原料 6 kg, 且每件 B 产品可获利 900 元,设生产 A 产品 x 件(产品件数为整数),根据以上信息解答下列问题:
例8
知2-练
解题秘方:从列不等式组求其解集中获取数据确定方案;由函数的增减性确定利润最大的方案 .
知2-练
(1)生产 A, B 两种产品的方案有哪几种?
知2-练
因为产品件数为整数,所以 x 取整数解 .
所以 x=18 或 x=19 或 x=20.
所以生产 A, B 两种产品的方案有如下三种:
方案一: A 产品 18 件, B 产品 12 件;
方案二: A 产品 19 件, B 产品 11 件;
方案三: A 产品 20 件, B 产品 10 件 .
知2-练
(2)设生产这 30 件产品可获利 y 元,写出 y 关于 x 的函数表达式,写出(1)中利润最大的方案,并求出最大利润 .
知2-练
解:由题意可得 y=700x+900(30-x)=-200x+27 000,因为 -200<0,所以 y 随 x 的增大而减小,
又因为 18 ≤ x ≤ 20,所以当 x=18 时有最大利润,
此时 y =-200×18+27 000=23 400.
答: (1)中利润最大的方案是方案一,即生产 A 产品 18 件,B 产品 12 件,最大利润为 23 400 元 .
知2-练
解法提醒
利用方程(组)、不等式(组)求解方案类问题的策略:
求解方案类问题时,应先正确建立函数模型,确定自变量的取值范围, 然后可利用函数的性质求最大(小)值; 或计算出各种方案的值进行大小比较,注意自变量的整数取值问题 .
综合与实践
一次函数模型的应用
用一次函数
解决问题
用函数图象解决问题
用函数性质解决问题
