13.1.1 三角形中边的关系(1)课件(共38张PPT)
文档属性
| 名称 | 13.1.1 三角形中边的关系(1)课件(共38张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-07 22:52:39 | ||
图片预览









文档简介
(共38张PPT)
逐点
导讲练
课堂小结
作业提升
课时讲解
1
课时流程
2
三角形的相关元素
三角形按边分类
三角形的三边关系
知1-讲
知识点
三角形的相关元素
1
1. 三角形的定义
由不在同一条直线上的三条线段首尾顺次相接所组成的封闭图形叫做三角形 .
三角形的表示法: 用符号“△”表示三角形,如图 13.1.1-1,顶点是 A, B, C 的三角形,记作“△ ABC”,读作“三角形ABC”.
字母的顺序可以自由安排
知1-讲
特别解读
1. 三角形的“三要素”:
(1)三条线段;
(2)三个顶点不在同一条直线上;
(3)三条线段首尾顺次相接 .
2. 三角形的边是一条线段,既可用两个顶点的大写字母表示,也可用边所对的顶点的小写字母表示,如顶点 A 所对的边 BC 可用 a 表示 .
2. 三角形的“三元素”
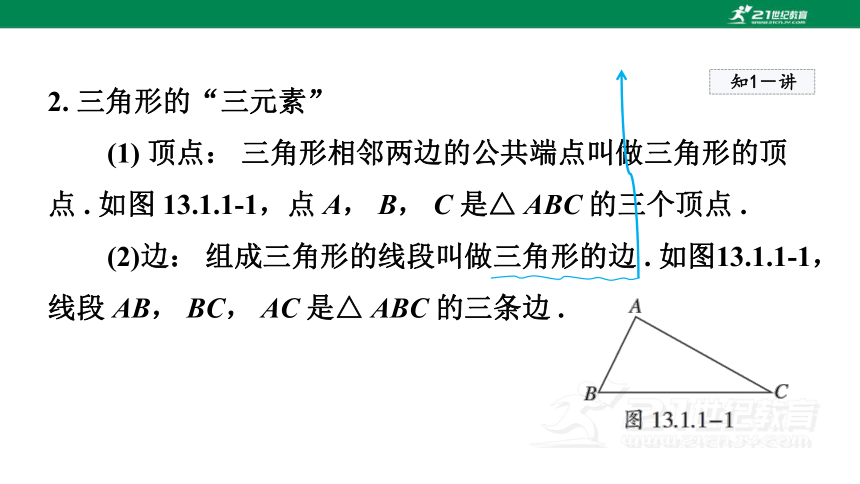
(1) 顶点: 三角形相邻两边的公共端点叫做三角形的顶点 . 如图 13.1.1-1,点 A, B, C 是△ ABC 的三个顶点 .
(2)边: 组成三角形的线段叫做三角形的边 . 如图13.1.1-1,线段 AB, BC, AC 是△ ABC 的三条边 .
知1-讲
(3) 内角: 在三角形中,相邻两边所组成的角叫做三角形的内角,简称三角形的角 . 如图 13.1.1-1,∠ A,∠ B,∠ C 是△ ABC 的三个角 .
知1-讲
知1-练
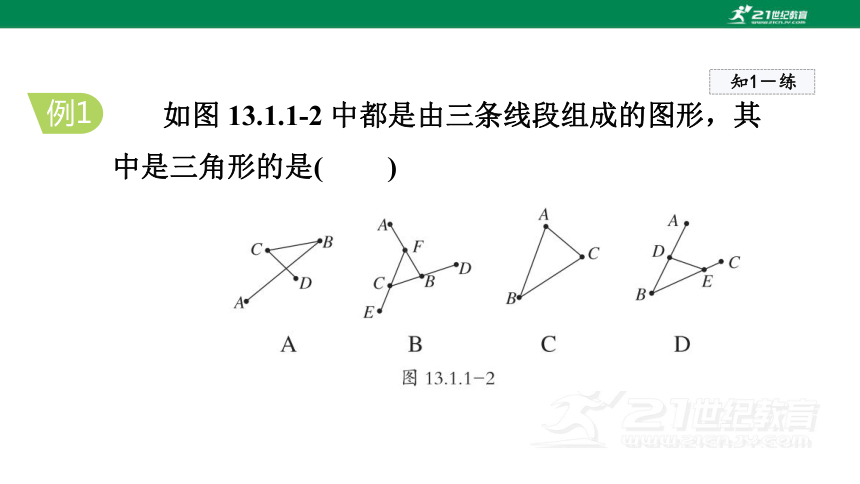
如图 13.1.1-2 中都是由三条线段组成的图形,其中是三角形的是( )
例1
知1-练
特别提醒
图形是三角形与图形内含有三角形是两个不同的概念 . 图形是三角形表示整个图形是一个三角形,图形内含有三角形表示图形局部有三角形,如选 项 A,B,D 中的图形内都含有三角形,但整个图形不是三角形 .
知1-练
解:选项 A, B, C, D 都是由三条线段组成的图形,但选项 A,B, D不是首尾顺次相接,因此只有选项C符合三角形的“三要素”.
解题秘方:紧扣三角形的“三要素”进行识别 .
答案:C
知1-练
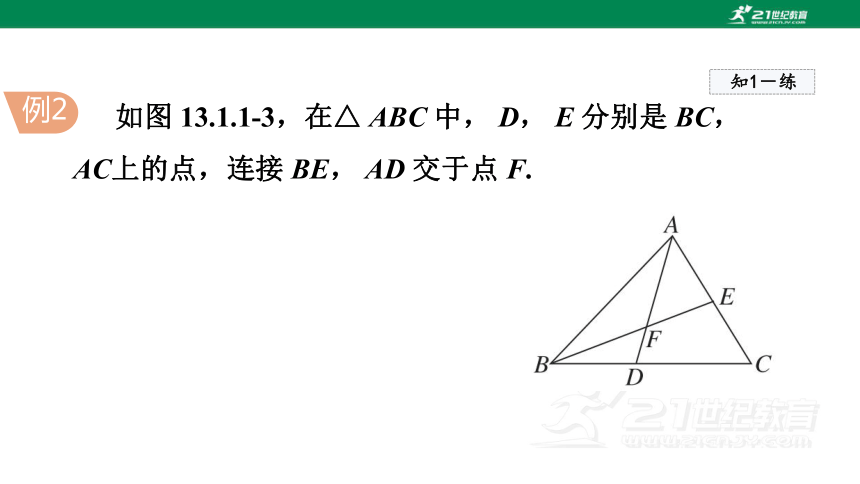
如图 13.1.1-3,在△ ABC 中, D, E 分别是 BC, AC上的点,连接 BE, AD 交于点 F.
例2
知1-练
解题秘方:紧扣“三角形及其元素的定义”及几何图形计数的常用方法进行解答 .
方法点拨
几何图形计数的常用方法:
1. 按序计数法;
2. 画图计数法;
3. 基本图形计数法;
4. 分类计数法 .
知1-练
(1)图中共有多少个三角形?请把它们表示出来 .
解:图中共有 8 个三角形,分别是△ ABF,
△ AEF,△ ABE,△ ABD,△ ACD,△ ABC,△ BDF,△ BCE.
知1-练
(2) △ BDF 的三个顶点是什么?三条边是什么?三个内角呢?
解:△ BDF 的三个顶点是点 B, D, F,
三条边是线段 BD, DF, BF,
三个内角是∠ FBD,∠ FDB,∠ BFD.
知1-练
(3)以 AB 为边的三角形有哪些?
解:以 AB 为边的三角形有△ ABF,△ ABD,△ ABE,△ ABC.
知1-练
(4)以∠ C 为内角的三角形有哪些?
解:以∠ C 为内角的三角形有△ ACD,△ BCE,△ ACB.
知1-练
特别提醒
三角形的三个顶点的字母的次序可以任意调换 ,如△ ABF 也可以写成△ BAF, △ BFA,△ FAB 等 .
知2-讲
知识点
三角形按边分类
2
知2-讲
分类示意图如图 13.1.1-4.
知2-讲
特别提醒
对三角形进行分类时,原则是不重复,不遗漏 .
知2-讲
2. 等腰三角形
有两条边相等的三角形叫做等腰三角形,其中相等的两边都叫做腰,第三边叫做底边,两腰的夹角叫做顶角,腰与底边的夹角叫做底角 .(如图 13.1.1-5)
特别地, 三边都相等的三角形叫做等边三角形,即底边与腰相等的等腰三角形叫做等边三角形,又叫做正三角形 .
知2-练
[ 易错题 ] 下列说法:①三角形按边分类可分为不等边三角形、等腰三角形和等边三角形;②等边三角形一定是等腰三角形;③有两边相等的三角形一定是等腰三角形 . 其中正确的有( )
A. 1 个 B. 2 个
C. 3 个 D. 0 个
例3
知2-练
答案:B
解:等边三角形是特殊的等腰三角形,它属于等腰三角形,故①错误;②正确;③为等腰三角形的定义,故正确 .
知2-练
易错警示
在按边分类时,等边三角形属于等腰三角形,不能单独作为一类 .
知3-讲
知识点
三角形的三边关系
3
1.三角形的三边关系
文字语言 数学语言 理论依据 图形
三角形中任何 两边的和大于 第三边 a+b > c,
b+c > a, a+c > b 两点之间 线段最短
三角形中任何 两边的差小于 第三边 a-b < c, b-c < a,a-c < b(a > b > c)
知3-讲
2. 三角形三边关系的应用
(1)判断三条线段能否组成三角形;
(2)已知三角形的两边长,确定第三边长(或周长)的取值范围;
(3)三角形的边长用字母表示时,求字母的取值范围;
(4)说明线段的不等关系 .
知3-讲
特别提醒
◆三角形中的“两边” 指任意两边,应用时常选取两条较短的边的和与第三边作比较,选取最长边与最短边的差与第三边作比较 .
◆已知三角形两边长a,b(a>b), 根据三角形的三边关系可知,第三边长 c 的取值范围是a - b< c知3-练
[ 中考·金华 ] 已知三角形的两边长分别为 5 cm 和8 cm,则第三边的长可以是( )
A. 2cm B. 3cm
C. 6cm D. 13cm
例4
知3-练
答案:C
解题秘方:紧扣“三角形的三边关系”进行判断 .
解:设第三边的长为 x cm,
因为三角形的两边长分别为 5 cm 和 8 cm,
所以 8 - 5 < x < 8+5,所以 3 < x < 13.
知3-练
技巧提醒
确定三条线段能否组成三角形的两种方法:
1. 看较短的两条线段的和是否大于最长的线段,若是,则能组成三角形;反之,则不能组成三角形 .
2. 看最长的线段减去最短的线段的差是否小于第三条线段,若是,则能组成三角形;反之,则不能组成三角形 .
知3-练
[ 中考·大庆 ] 三个数 3, 1 - a, 1 - 2a 在数轴上从左到右依次排列,且以这三个数为边长能构成三角形,则 a 的取值范围为___________.
例5
知3-练
解题秘方:由三个数的大小关系初步确定 a 的取值范围为 a < - 2;再紧扣三角形的三边关系得到 3+(1 - a)> 1 - 2a,从而求出 a 的取值范围.
知3-练
答案: - 3 < a < - 2
解:因为 3,1 - a,1 - 2a 在数轴上从左到右依次排列,所以 3 < 1 - a < 1 - 2a.
所以 a < - 2.
因为以这三个数为边长能构成三角形,
所以 3+(1 - a)> 1 - 2a. 所以 a > - 3.
所以- 3 < a < - 2.
知3-练
方法点拨
已知某三条线段能围成一个三角形,则其中任何一边都小于另两边之和,大于另两边之差,据此既可以解决“已知两边长,求第三边长的取值范围”,也可以解决“ 用字母表示三角形边长时字母的取值范围”.
知3-练
如图 13.1.1-6,已知点 D 是△ ABC 内一点.试说明:
(1) BD+CD < AB+AC;
(2) AD+BD+CD < AB+BC+AC.
例6
知3-练
解法提醒
说明线段和 的大小关系,首先要把这些分散的线段集中,构造三角形,并运用“三角形任意两边的和大于第三边”这一关系,得出几个同向不等式,然后根据不等式的性质等知识,得出结论 .
知3-练
解题秘方:紧扣“三角形的三边关系”将要说明的线段转化到三角形三边中去说明 .
知3-练
解:(1)如图 13.1.1-7,延长 BD 交 AC 于点 E,
在△ ABE 中,有 AB+AE > BE,
在△ EDC 中,有 ED+EC > CD,
所以 AB+AE+ED+EC > BE+CD.
因为 AE+EC = AC, BE = BD+DE,
所以 AB+AC+ED > BD+DE+CD.
所以 AB+AC > BD+CD. 即 BD+CD < AB+AC.
知3-练
解:(2)由(1)同理可得: AD+CD < AB+BC,BD+AD < BC+AC,
又因为 BD+CD < AB+AC,
所以 2(AD+BD+CD)< 2(AB+BC+AC).
所以 AD+BD+CD < AB+BC+AC.
三角形中边的关系
三边关系
组成
元素
不等边
三角形
分类
三角形
边
角
顶点
等腰
三角形
按边分类
逐点
导讲练
课堂小结
作业提升
课时讲解
1
课时流程
2
三角形的相关元素
三角形按边分类
三角形的三边关系
知1-讲
知识点
三角形的相关元素
1
1. 三角形的定义
由不在同一条直线上的三条线段首尾顺次相接所组成的封闭图形叫做三角形 .
三角形的表示法: 用符号“△”表示三角形,如图 13.1.1-1,顶点是 A, B, C 的三角形,记作“△ ABC”,读作“三角形ABC”.
字母的顺序可以自由安排
知1-讲
特别解读
1. 三角形的“三要素”:
(1)三条线段;
(2)三个顶点不在同一条直线上;
(3)三条线段首尾顺次相接 .
2. 三角形的边是一条线段,既可用两个顶点的大写字母表示,也可用边所对的顶点的小写字母表示,如顶点 A 所对的边 BC 可用 a 表示 .
2. 三角形的“三元素”
(1) 顶点: 三角形相邻两边的公共端点叫做三角形的顶点 . 如图 13.1.1-1,点 A, B, C 是△ ABC 的三个顶点 .
(2)边: 组成三角形的线段叫做三角形的边 . 如图13.1.1-1,线段 AB, BC, AC 是△ ABC 的三条边 .
知1-讲
(3) 内角: 在三角形中,相邻两边所组成的角叫做三角形的内角,简称三角形的角 . 如图 13.1.1-1,∠ A,∠ B,∠ C 是△ ABC 的三个角 .
知1-讲
知1-练
如图 13.1.1-2 中都是由三条线段组成的图形,其中是三角形的是( )
例1
知1-练
特别提醒
图形是三角形与图形内含有三角形是两个不同的概念 . 图形是三角形表示整个图形是一个三角形,图形内含有三角形表示图形局部有三角形,如选 项 A,B,D 中的图形内都含有三角形,但整个图形不是三角形 .
知1-练
解:选项 A, B, C, D 都是由三条线段组成的图形,但选项 A,B, D不是首尾顺次相接,因此只有选项C符合三角形的“三要素”.
解题秘方:紧扣三角形的“三要素”进行识别 .
答案:C
知1-练
如图 13.1.1-3,在△ ABC 中, D, E 分别是 BC, AC上的点,连接 BE, AD 交于点 F.
例2
知1-练
解题秘方:紧扣“三角形及其元素的定义”及几何图形计数的常用方法进行解答 .
方法点拨
几何图形计数的常用方法:
1. 按序计数法;
2. 画图计数法;
3. 基本图形计数法;
4. 分类计数法 .
知1-练
(1)图中共有多少个三角形?请把它们表示出来 .
解:图中共有 8 个三角形,分别是△ ABF,
△ AEF,△ ABE,△ ABD,△ ACD,△ ABC,△ BDF,△ BCE.
知1-练
(2) △ BDF 的三个顶点是什么?三条边是什么?三个内角呢?
解:△ BDF 的三个顶点是点 B, D, F,
三条边是线段 BD, DF, BF,
三个内角是∠ FBD,∠ FDB,∠ BFD.
知1-练
(3)以 AB 为边的三角形有哪些?
解:以 AB 为边的三角形有△ ABF,△ ABD,△ ABE,△ ABC.
知1-练
(4)以∠ C 为内角的三角形有哪些?
解:以∠ C 为内角的三角形有△ ACD,△ BCE,△ ACB.
知1-练
特别提醒
三角形的三个顶点的字母的次序可以任意调换 ,如△ ABF 也可以写成△ BAF, △ BFA,△ FAB 等 .
知2-讲
知识点
三角形按边分类
2
知2-讲
分类示意图如图 13.1.1-4.
知2-讲
特别提醒
对三角形进行分类时,原则是不重复,不遗漏 .
知2-讲
2. 等腰三角形
有两条边相等的三角形叫做等腰三角形,其中相等的两边都叫做腰,第三边叫做底边,两腰的夹角叫做顶角,腰与底边的夹角叫做底角 .(如图 13.1.1-5)
特别地, 三边都相等的三角形叫做等边三角形,即底边与腰相等的等腰三角形叫做等边三角形,又叫做正三角形 .
知2-练
[ 易错题 ] 下列说法:①三角形按边分类可分为不等边三角形、等腰三角形和等边三角形;②等边三角形一定是等腰三角形;③有两边相等的三角形一定是等腰三角形 . 其中正确的有( )
A. 1 个 B. 2 个
C. 3 个 D. 0 个
例3
知2-练
答案:B
解:等边三角形是特殊的等腰三角形,它属于等腰三角形,故①错误;②正确;③为等腰三角形的定义,故正确 .
知2-练
易错警示
在按边分类时,等边三角形属于等腰三角形,不能单独作为一类 .
知3-讲
知识点
三角形的三边关系
3
1.三角形的三边关系
文字语言 数学语言 理论依据 图形
三角形中任何 两边的和大于 第三边 a+b > c,
b+c > a, a+c > b 两点之间 线段最短
三角形中任何 两边的差小于 第三边 a-b < c, b-c < a,a-c < b(a > b > c)
知3-讲
2. 三角形三边关系的应用
(1)判断三条线段能否组成三角形;
(2)已知三角形的两边长,确定第三边长(或周长)的取值范围;
(3)三角形的边长用字母表示时,求字母的取值范围;
(4)说明线段的不等关系 .
知3-讲
特别提醒
◆三角形中的“两边” 指任意两边,应用时常选取两条较短的边的和与第三边作比较,选取最长边与最短边的差与第三边作比较 .
◆已知三角形两边长a,b(a>b), 根据三角形的三边关系可知,第三边长 c 的取值范围是a - b< c
[ 中考·金华 ] 已知三角形的两边长分别为 5 cm 和8 cm,则第三边的长可以是( )
A. 2cm B. 3cm
C. 6cm D. 13cm
例4
知3-练
答案:C
解题秘方:紧扣“三角形的三边关系”进行判断 .
解:设第三边的长为 x cm,
因为三角形的两边长分别为 5 cm 和 8 cm,
所以 8 - 5 < x < 8+5,所以 3 < x < 13.
知3-练
技巧提醒
确定三条线段能否组成三角形的两种方法:
1. 看较短的两条线段的和是否大于最长的线段,若是,则能组成三角形;反之,则不能组成三角形 .
2. 看最长的线段减去最短的线段的差是否小于第三条线段,若是,则能组成三角形;反之,则不能组成三角形 .
知3-练
[ 中考·大庆 ] 三个数 3, 1 - a, 1 - 2a 在数轴上从左到右依次排列,且以这三个数为边长能构成三角形,则 a 的取值范围为___________.
例5
知3-练
解题秘方:由三个数的大小关系初步确定 a 的取值范围为 a < - 2;再紧扣三角形的三边关系得到 3+(1 - a)> 1 - 2a,从而求出 a 的取值范围.
知3-练
答案: - 3 < a < - 2
解:因为 3,1 - a,1 - 2a 在数轴上从左到右依次排列,所以 3 < 1 - a < 1 - 2a.
所以 a < - 2.
因为以这三个数为边长能构成三角形,
所以 3+(1 - a)> 1 - 2a. 所以 a > - 3.
所以- 3 < a < - 2.
知3-练
方法点拨
已知某三条线段能围成一个三角形,则其中任何一边都小于另两边之和,大于另两边之差,据此既可以解决“已知两边长,求第三边长的取值范围”,也可以解决“ 用字母表示三角形边长时字母的取值范围”.
知3-练
如图 13.1.1-6,已知点 D 是△ ABC 内一点.试说明:
(1) BD+CD < AB+AC;
(2) AD+BD+CD < AB+BC+AC.
例6
知3-练
解法提醒
说明线段和 的大小关系,首先要把这些分散的线段集中,构造三角形,并运用“三角形任意两边的和大于第三边”这一关系,得出几个同向不等式,然后根据不等式的性质等知识,得出结论 .
知3-练
解题秘方:紧扣“三角形的三边关系”将要说明的线段转化到三角形三边中去说明 .
知3-练
解:(1)如图 13.1.1-7,延长 BD 交 AC 于点 E,
在△ ABE 中,有 AB+AE > BE,
在△ EDC 中,有 ED+EC > CD,
所以 AB+AE+ED+EC > BE+CD.
因为 AE+EC = AC, BE = BD+DE,
所以 AB+AC+ED > BD+DE+CD.
所以 AB+AC > BD+CD. 即 BD+CD < AB+AC.
知3-练
解:(2)由(1)同理可得: AD+CD < AB+BC,BD+AD < BC+AC,
又因为 BD+CD < AB+AC,
所以 2(AD+BD+CD)< 2(AB+BC+AC).
所以 AD+BD+CD < AB+BC+AC.
三角形中边的关系
三边关系
组成
元素
不等边
三角形
分类
三角形
边
角
顶点
等腰
三角形
按边分类
