浙江省绍兴市柯桥区联盟学校2024-2025学年七年级下学期6月月考数学试卷(含手写答案)
文档属性
| 名称 | 浙江省绍兴市柯桥区联盟学校2024-2025学年七年级下学期6月月考数学试卷(含手写答案) |  | |
| 格式 | docx | ||
| 文件大小 | 574.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-06 22:05:20 | ||
图片预览


文档简介
2024学年第二学期七年级数学学科课堂作业调测卷
一、选择题(每小题3分,共30分,在每小题给出的四个选项中,只有一项符合题目要求)
1.下列方程中,是二元一次方程的是( )
A.x+y=1 B.xy=1 C. D.x2﹣x﹣1=0
2.若要调查下列问题,你认为适合采用全面调查的是( )
A.对全国中学生每天睡眠时长情况的调查 B.对一批节能灯的使用寿命的调查
C.对柯桥区城湾水库水质情况的调查D.对载人航天飞船发射前各零部件质量情况的调查
3.下列运算正确的是( )
A.a2 a4=a6 B.a2+a6=a8 C.(a2)4=a6 D.a8÷a4=a2
4.随着半导体芯片市场的不断发展,手机芯片的工艺也从7nm到5nm,再到如今最先进的3nm工艺,性能也越来越强,已知3nm=0.000000003m,其中0.000000003用科学记数法表示为( )A.0.3×10﹣9 B.3×10﹣9 C.3×10﹣8 D.0.3×10﹣8
5.下列等式从左到右的变形,属于因式分解的是( )
A.a(x+y)=ax+ay B.x2﹣9=(x+3)(x﹣3)
C.﹣8x2y3=﹣2xy 4xy2 D.x2+2x+1=x(x+2)+1
6.将一张两边平行的纸条如图折叠一下,若∠1=40°,则∠2的度数是( )
A.50° B.60° C.70° D.80°
7.如果把分式中的x和y都扩大为原来的3倍,那么分式的值( )
A.扩大为原来的9倍 B.扩大为原来的3倍
C.不变 D.缩小为原来的
8.现有如图所示的卡片若干张,其中A型、B型为正方形卡片,C型为长方形卡片,若要用这三种类型卡片拼成一个长为3a+b,宽为a+2b的大长方形,则需要C型卡片的张数为( )
A.4 B.5 C.6 D.7
9.劳技课上学生用铁皮制作收纳盒,每张铁皮可制作盒身4个,或制作盒底6个,一个盒身与两个盒底配成一个收纳盒.现有材料28张铁皮,设用x张制作盒身,y张制作盒底,恰好配套制成收纳盒.则下列方程组中符合题意的是( )A. B. C. D.
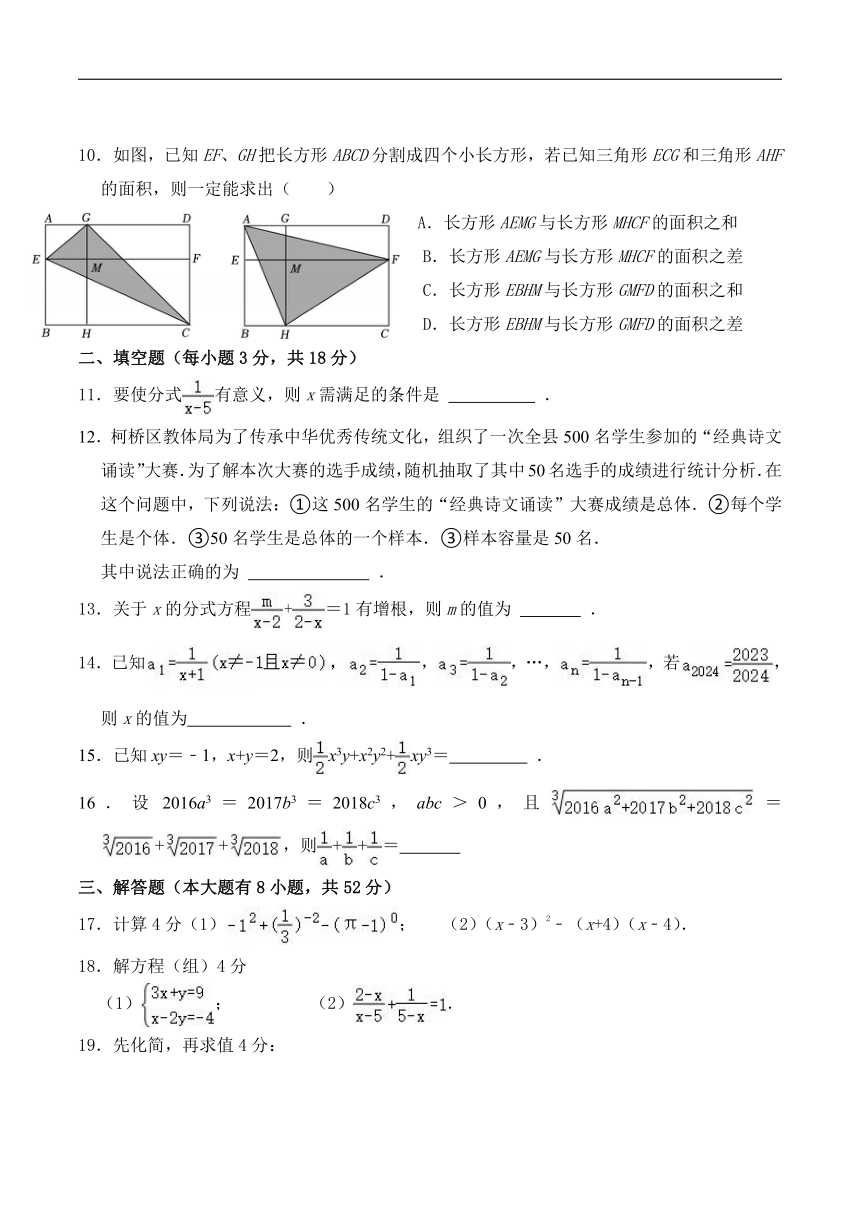
如图,已知EF、GH把长方形ABCD分割成四个小长方形,若已知三角形ECG和三角形AHF的面积,则一定能求出( )
A.长方形AEMG与长方形MHCF的面积之和
B.长方形AEMG与长方形MHCF的面积之差
C.长方形EBHM与长方形GMFD的面积之和
D.长方形EBHM与长方形GMFD的面积之差
二、填空题(每小题3分,共18分)
11.要使分式有意义,则x需满足的条件是 .
12.柯桥区教体局为了传承中华优秀传统文化,组织了一次全县500名学生参加的“经典诗文诵读”大赛.为了解本次大赛的选手成绩,随机抽取了其中50名选手的成绩进行统计分析.在这个问题中,下列说法:①这500名学生的“经典诗文诵读”大赛成绩是总体.②每个学生是个体.③50名学生是总体的一个样本.③样本容量是50名.
其中说法正确的为 .
13.关于x的分式方程+=1有增根,则m的值为 .
14.已知,,…,,若,则x的值为 .
15.已知xy=﹣1,x+y=2,则x3y+x2y2+xy3= .
16.设2016a3=2017b3=2018c3,abc>0,且=++,则++=
三、解答题(本大题有8小题,共52分)
17.计算4分(1); (2)(x﹣3)2﹣(x+4)(x﹣4).
18.解方程(组)4分
(1); (2).
19.先化简,再求值4分:
,其中x从0,1,2中选取一个合适的值代入.
20.(6分)如图,点D,E分别在△ABC的边AB,AC上,点F在线段BE上,且∠EDF=∠C,DE∥BC.
(1)判断DF与AC的位置关系,并说明理由;
(2)若DF平分∠BDE,∠ADE=38°,求∠AED.
21.(8分)临近期末,某校七年级一班打算购买一些记录本和笔作为休学式当天班内学期表彰的奖品.已知一本记录本的价格比一支笔的价格高1元,用180元可以购得的本子数量和用150元可以购得的笔的数量相同.
(1)求记录本和笔的单价.
(2)本次计划使用120元班费全部用于购买记录本和笔(经费无剩余且两种奖品都要购买),请问有哪几种购买方案?
22.(8分)【基础巩固】从课本中我们学习了因式分解的常见方法:提取公因式法和公式法.
(1)填空:因式分解3x2﹣6x+3= .
【思考探究】在学习过程中,我们还发现存在某些多项式既没有公因式,也不能直接运用公式分解因式,但是某些项通过适当的调整能构成可分解的一组,用分组来分解一个多项式的因式,这种方法叫分组分解法.例如:“x2﹣y2+3x+3y”,细心观察这个式子就会发现,前两项可以因式分解,后两项也可因式分解,前后两部分分别分解因式后产生了新的公因式,然后再提取公因式,具体过程为
x2﹣y2+3x+3y=(x2﹣y2)+(3x+3y)=(x+y)(x﹣y)+3(x+y)=(x+y)(x﹣y+3).
(2)请在上述方法的启发下,分解下列因式:
①x2﹣xy+6x﹣6y; ②m2﹣n2+6m+9.
【应用尝试】(3)已知实数a,b满足2a2﹣4a+4+2ab+b2=0,求a﹣b的值.
23.(8分)我们把形如x+=a+b(a,b不为零),且两个解分别为x1=a,x2=b的方程称为“十字分式方程”.
例如x+=4为十字分式方程,可化为x+=1+3,∴x1=1,x2=3.
再如x+=﹣6为十字分式方程,可化为x+=(﹣2)+(﹣4),
∴x1=﹣2,x2=﹣4.
应用上面的结论解答下列问题:
(1)若x+=﹣5为十字分式方程,则x1= ,x2= .
(2)若十字分式方程x﹣=﹣2的两个解分别为x1=m,x2=n,求的值.
(10分)如图1,已知直线AB∥CD,点E在直线AB上,点F在直线CD上,在直线AB、CD同侧有一点P,连结EP、FP.
(1)①若∠PEB=30°,∠PFD=70°,求∠P= .
②设∠PEB=α、∠PFD=β,则∠P= .(用含α、β的代数式表示)
(2)如图2,取直线AB、CD间一点G,过点G、E作射线GM,过点G、F作射线GN.若PE平分∠MEB,PF平分∠GFD,试猜想∠P与∠G的数量关系,并说明理由.
(3)在(2)的条件下,Q为直线CD上一点,过点Q作QH∥GN交直线PF于点H,若∠G=60°,∠PEB=25°,∠FPQ=20°,请直接写出∠HQP= .
声明:试题解析著作权属所有,未经书面同意,不得复制发布日期:2025/5/19 14:13:01;用
一、选择题(每小题3分,共30分,在每小题给出的四个选项中,只有一项符合题目要求)
1.下列方程中,是二元一次方程的是( )
A.x+y=1 B.xy=1 C. D.x2﹣x﹣1=0
2.若要调查下列问题,你认为适合采用全面调查的是( )
A.对全国中学生每天睡眠时长情况的调查 B.对一批节能灯的使用寿命的调查
C.对柯桥区城湾水库水质情况的调查D.对载人航天飞船发射前各零部件质量情况的调查
3.下列运算正确的是( )
A.a2 a4=a6 B.a2+a6=a8 C.(a2)4=a6 D.a8÷a4=a2
4.随着半导体芯片市场的不断发展,手机芯片的工艺也从7nm到5nm,再到如今最先进的3nm工艺,性能也越来越强,已知3nm=0.000000003m,其中0.000000003用科学记数法表示为( )A.0.3×10﹣9 B.3×10﹣9 C.3×10﹣8 D.0.3×10﹣8
5.下列等式从左到右的变形,属于因式分解的是( )
A.a(x+y)=ax+ay B.x2﹣9=(x+3)(x﹣3)
C.﹣8x2y3=﹣2xy 4xy2 D.x2+2x+1=x(x+2)+1
6.将一张两边平行的纸条如图折叠一下,若∠1=40°,则∠2的度数是( )
A.50° B.60° C.70° D.80°
7.如果把分式中的x和y都扩大为原来的3倍,那么分式的值( )
A.扩大为原来的9倍 B.扩大为原来的3倍
C.不变 D.缩小为原来的
8.现有如图所示的卡片若干张,其中A型、B型为正方形卡片,C型为长方形卡片,若要用这三种类型卡片拼成一个长为3a+b,宽为a+2b的大长方形,则需要C型卡片的张数为( )
A.4 B.5 C.6 D.7
9.劳技课上学生用铁皮制作收纳盒,每张铁皮可制作盒身4个,或制作盒底6个,一个盒身与两个盒底配成一个收纳盒.现有材料28张铁皮,设用x张制作盒身,y张制作盒底,恰好配套制成收纳盒.则下列方程组中符合题意的是( )A. B. C. D.
如图,已知EF、GH把长方形ABCD分割成四个小长方形,若已知三角形ECG和三角形AHF的面积,则一定能求出( )
A.长方形AEMG与长方形MHCF的面积之和
B.长方形AEMG与长方形MHCF的面积之差
C.长方形EBHM与长方形GMFD的面积之和
D.长方形EBHM与长方形GMFD的面积之差
二、填空题(每小题3分,共18分)
11.要使分式有意义,则x需满足的条件是 .
12.柯桥区教体局为了传承中华优秀传统文化,组织了一次全县500名学生参加的“经典诗文诵读”大赛.为了解本次大赛的选手成绩,随机抽取了其中50名选手的成绩进行统计分析.在这个问题中,下列说法:①这500名学生的“经典诗文诵读”大赛成绩是总体.②每个学生是个体.③50名学生是总体的一个样本.③样本容量是50名.
其中说法正确的为 .
13.关于x的分式方程+=1有增根,则m的值为 .
14.已知,,…,,若,则x的值为 .
15.已知xy=﹣1,x+y=2,则x3y+x2y2+xy3= .
16.设2016a3=2017b3=2018c3,abc>0,且=++,则++=
三、解答题(本大题有8小题,共52分)
17.计算4分(1); (2)(x﹣3)2﹣(x+4)(x﹣4).
18.解方程(组)4分
(1); (2).
19.先化简,再求值4分:
,其中x从0,1,2中选取一个合适的值代入.
20.(6分)如图,点D,E分别在△ABC的边AB,AC上,点F在线段BE上,且∠EDF=∠C,DE∥BC.
(1)判断DF与AC的位置关系,并说明理由;
(2)若DF平分∠BDE,∠ADE=38°,求∠AED.
21.(8分)临近期末,某校七年级一班打算购买一些记录本和笔作为休学式当天班内学期表彰的奖品.已知一本记录本的价格比一支笔的价格高1元,用180元可以购得的本子数量和用150元可以购得的笔的数量相同.
(1)求记录本和笔的单价.
(2)本次计划使用120元班费全部用于购买记录本和笔(经费无剩余且两种奖品都要购买),请问有哪几种购买方案?
22.(8分)【基础巩固】从课本中我们学习了因式分解的常见方法:提取公因式法和公式法.
(1)填空:因式分解3x2﹣6x+3= .
【思考探究】在学习过程中,我们还发现存在某些多项式既没有公因式,也不能直接运用公式分解因式,但是某些项通过适当的调整能构成可分解的一组,用分组来分解一个多项式的因式,这种方法叫分组分解法.例如:“x2﹣y2+3x+3y”,细心观察这个式子就会发现,前两项可以因式分解,后两项也可因式分解,前后两部分分别分解因式后产生了新的公因式,然后再提取公因式,具体过程为
x2﹣y2+3x+3y=(x2﹣y2)+(3x+3y)=(x+y)(x﹣y)+3(x+y)=(x+y)(x﹣y+3).
(2)请在上述方法的启发下,分解下列因式:
①x2﹣xy+6x﹣6y; ②m2﹣n2+6m+9.
【应用尝试】(3)已知实数a,b满足2a2﹣4a+4+2ab+b2=0,求a﹣b的值.
23.(8分)我们把形如x+=a+b(a,b不为零),且两个解分别为x1=a,x2=b的方程称为“十字分式方程”.
例如x+=4为十字分式方程,可化为x+=1+3,∴x1=1,x2=3.
再如x+=﹣6为十字分式方程,可化为x+=(﹣2)+(﹣4),
∴x1=﹣2,x2=﹣4.
应用上面的结论解答下列问题:
(1)若x+=﹣5为十字分式方程,则x1= ,x2= .
(2)若十字分式方程x﹣=﹣2的两个解分别为x1=m,x2=n,求的值.
(10分)如图1,已知直线AB∥CD,点E在直线AB上,点F在直线CD上,在直线AB、CD同侧有一点P,连结EP、FP.
(1)①若∠PEB=30°,∠PFD=70°,求∠P= .
②设∠PEB=α、∠PFD=β,则∠P= .(用含α、β的代数式表示)
(2)如图2,取直线AB、CD间一点G,过点G、E作射线GM,过点G、F作射线GN.若PE平分∠MEB,PF平分∠GFD,试猜想∠P与∠G的数量关系,并说明理由.
(3)在(2)的条件下,Q为直线CD上一点,过点Q作QH∥GN交直线PF于点H,若∠G=60°,∠PEB=25°,∠FPQ=20°,请直接写出∠HQP= .
声明:试题解析著作权属所有,未经书面同意,不得复制发布日期:2025/5/19 14:13:01;用
同课章节目录
