2025届中考数学全真模拟卷 【江西专用】(含详解)
文档属性
| 名称 | 2025届中考数学全真模拟卷 【江西专用】(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-07 07:42:54 | ||
图片预览



文档简介
2025届中考数学全真模拟卷 【江西专用】
【满分120分 考试时间120分钟】
一、选择题(本大题共6小题,每小题3分,共18分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.[2024年辽宁中考真题]纹样是我国古代艺术中的瑰宝.下列四幅纹样图形既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.[2024年山东烟台中考真题]目前全球最薄的手撕钢产自中国,厚度只有0.015毫米,约是A4纸厚度的六分之一,已知1毫米百万纳米,0.015毫米等于多少纳米?将结果用科学记数法表示为( )
A.纳米 B.纳米 C.纳米 D.纳米
3.[2024年山东枣庄中考真题]下列运算正确的是( )
A. B.
C. D.
4.[2024年四川雅安中考真题]某校开展了红色经典故事演讲比赛,其中8名同学的成绩(单位:分)分别为:85,81,82,86,82,83,92,89.关于这组数据,下列说法中正确的是( )
A.众数是92 B.中位数是
C.平均数是84 D.方差是13
5.[2024年山东泰安中考真题]如图,AB是的直径,C,D是上两点,BA平分,若,则的度数为( )
A. B. C. D.
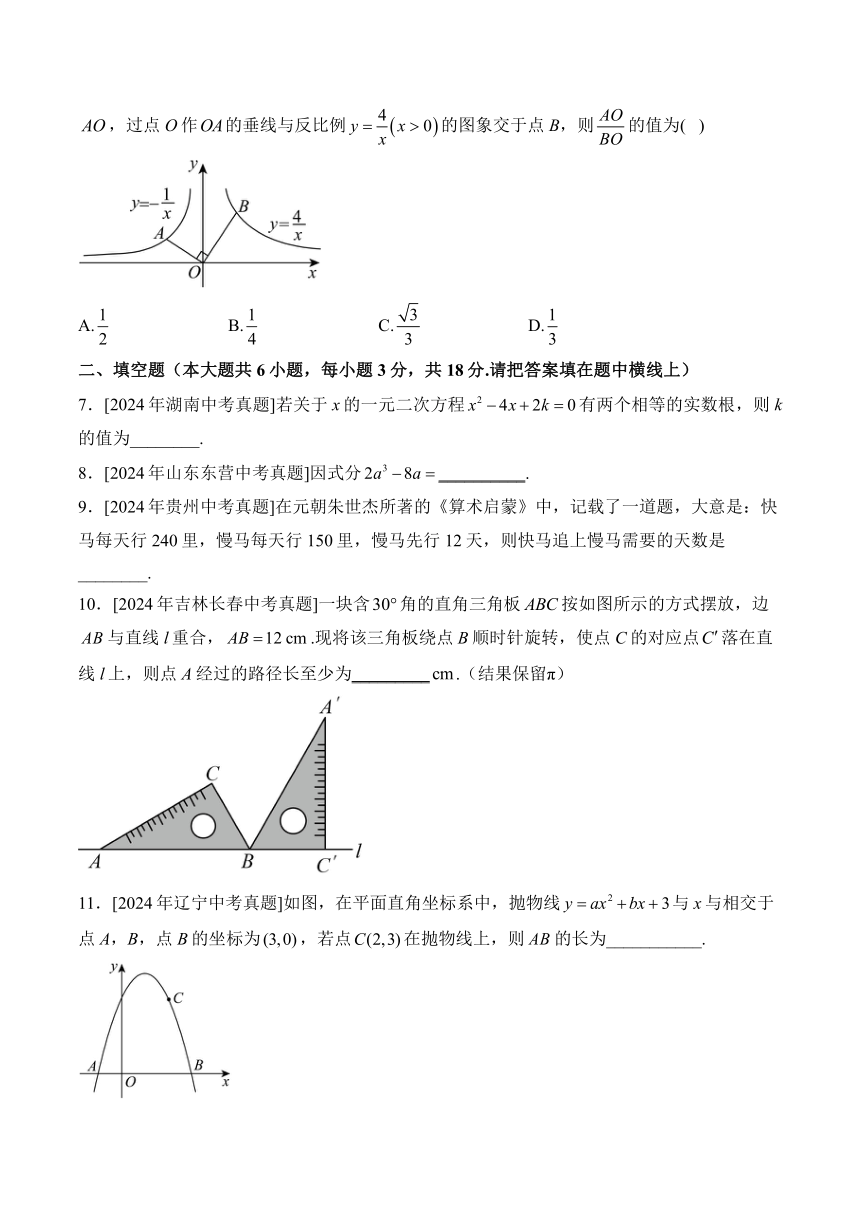
6.[2024年江苏苏州中考真题]如图,点A为反比例函数图象上的一点,连接,过点O作的垂线与反比例的图象交于点B,则的值为( )
A. B. C. D.
二、填空题(本大题共6小题,每小题3分,共18分.请把答案填在题中横线上)
7.[2024年湖南中考真题]若关于x的一元二次方程有两个相等的实数根,则k的值为________.
8.[2024年山东东营中考真题]因式分__________.
9.[2024年贵州中考真题]在元朝朱世杰所著的《算术启蒙》中,记载了一道题,大意是:快马每天行240里,慢马每天行150里,慢马先行12天,则快马追上慢马需要的天数是________.
10.[2024年吉林长春中考真题]一块含角的直角三角板按如图所示的方式摆放,边与直线l重合,.现将该三角板绕点B顺时针旋转,使点C的对应点落在直线l上,则点A经过的路径长至少为_________.(结果保留π)
11.[2024年辽宁中考真题]如图,在平面直角坐标系中,抛物线与x与相交于点A,B,点B的坐标为,若点在抛物线上,则的长为___________.
12.[2024年江苏宿迁中考真题]如图,在平面直角坐标系中,点A在直线上,且点A的横坐标为4,直角三角板的直角顶点C落在x轴上,一条直角边经过点A,另一条直角边与直线交于点B,当点C在x轴上移动时,线段的最小值为_________.
三、解答题(本大题共11小题,共84分.解答应写出必要的文字说明,证明过程或演算步骤)
13.(6分)[2024年江苏镇江中考真题](1)计算:;
(2)化简:.
14.(6分)[2024年江苏镇江中考真题]3张相同的卡片上分别写有中国二十四节气中的“小满”、“芒种”、“夏至”的字样,将卡片的背面朝上.
(1)洗匀后,从中任意抽取1张卡片,抽到写有“小满”的卡片的概率等于__________;
(2)洗匀后,从中任意抽取2张卡片,用画树状图或列表的方法,求抽到一张写有“芒种”,一张写有“夏至”的卡片的概率.
15.(6分)[2024年江苏无锡中考真题]如图,在矩形中,E是的中点,连接,.求证:
(1);
(2).
16.(6分)[2024年四川泸州中考真题]某商场购进A,B两种商品,已知购进3件A商品比购进4件B商品费用多60元;购进5件A商品和2件B商品总费用为620元.
(1)求A,B两种商品每件进价各为多少元?
(2)该商场计划购进A,B两种商品共60件,且购进B商品的件数不少于A商品件数的2倍.若A商品按每件150元销售,B商品按每件80元销售,为满足销售完A,B两种商品后获得的总利润不低于1770元,则购进A商品的件数最多为多少?
17.(6分)[2024年广西中考真题]如图,在中,,.
(1)尺规作图:作线段的垂直平分线l,分别交,于点D,E:(要求:保留作图痕迹,不写作法,标明字母)
(2)在(1)所作的图中,连接,若,求的长.
18.(8分)[2024年内蒙古中考真题]如图,在平行四边形中,点F在边上,,连接,点O为的中点,的延长线交边于点E,连接
(1)求证:四边形是菱形;
(2)若平行四边形的周长为22,,,求的长.
19.(8分)[2024年山东东营中考真题]如图,内接于,是的直径,点E在上,点C是的中点,,垂足为点D,DC的延长线交AB的延长线于点F.
(1)求证:CD是的切线;
(2)若,,求线段AF的长.
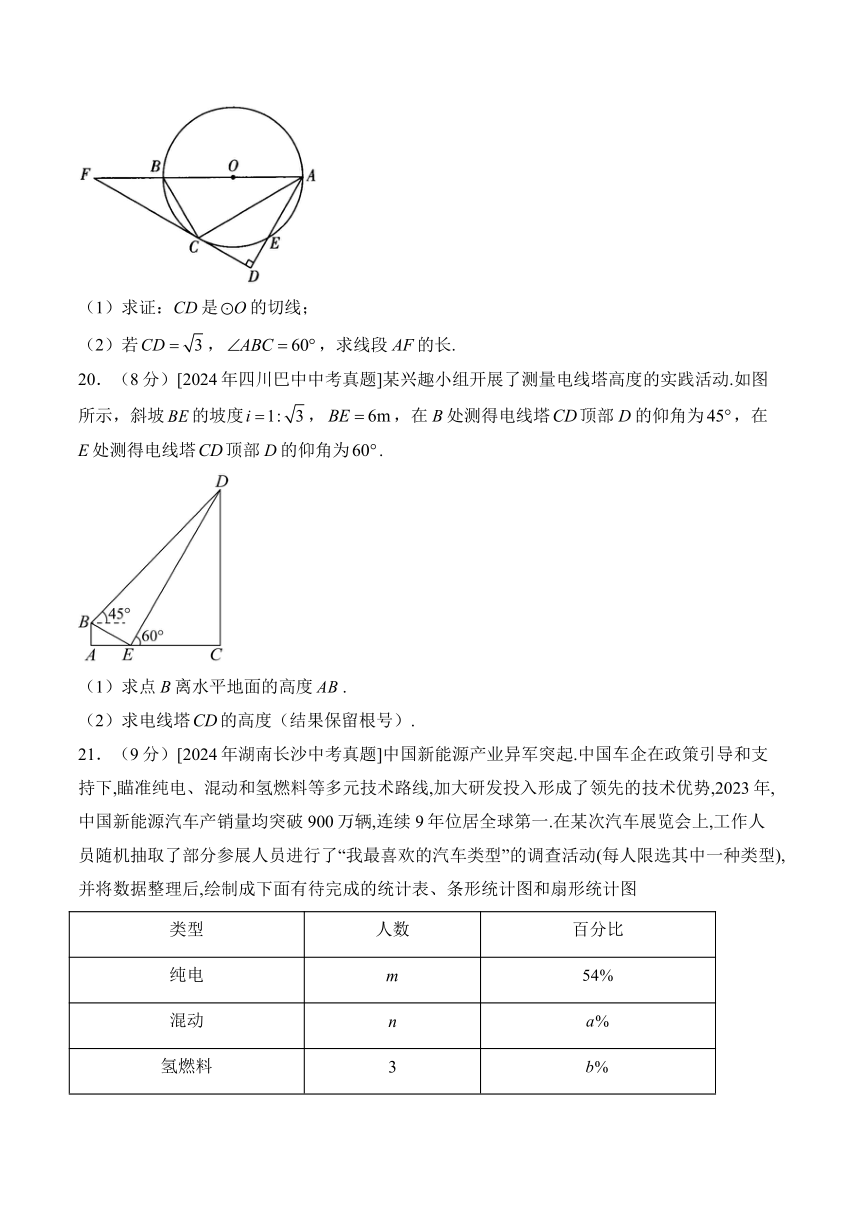
20.(8分)[2024年四川巴中中考真题]某兴趣小组开展了测量电线塔高度的实践活动.如图所示,斜坡的坡度,,在B处测得电线塔顶部D的仰角为,在E处测得电线塔顶部D的仰角为.
(1)求点B离水平地面的高度.
(2)求电线塔的高度(结果保留根号).
21.(9分)[2024年湖南长沙中考真题]中国新能源产业异军突起.中国车企在政策引导和支持下,瞄准纯电、混动和氢燃料等多元技术路线,加大研发投入形成了领先的技术优势,2023年,中国新能源汽车产销量均突破900万辆,连续9年位居全球第一.在某次汽车展览会上,工作人员随机抽取了部分参展人员进行了“我最喜欢的汽车类型”的调查活动(每人限选其中一种类型),并将数据整理后,绘制成下面有待完成的统计表、条形统计图和扇形统计图
类型 人数 百分比
纯电 m
混动 n
氢燃料 3
油车 5
请根据以上信息,解答下列问题:
(1)本次调查活动随机抽取了_____人;表中______,______;
(2)请补全条形统计图;
(3)请计算扇形统计图中“混动”类所在扇形的圆心角的度数;
(4)若此次汽车展览会的参展人员共有4000人,请你估计喜欢新能源(纯电、混动、氢燃料)汽车的有多少人?
22.(9分)[2024年江苏苏州中考真题]如图,中,,,,,反比例函数的图象与交于点,与交于点E.
(1)求m,k的值;
(2)点P为反比例函数图象上一动点(点P在D,E之间运动,不与D,E重合),过点P作,交y轴于点M,过点P作轴,交于点N,连接,求面积的最大值,并求出此时点P的坐标.
23.(12分)[2024年湖北武汉中考真题]问题背景:如图(1),在矩形中,点E,F分别是,的中点,连接,,求证:.
问题探究:如图(2),在四边形中,,,点E是的中点,点F在边上,,与交于点G,求证:.
问题拓展:如图(3),在“问题探究”的条件下,连接,,,直接写出的值.
参考答案
1.答案:B
解析:A、既不是轴对称图形也不是中心对称图形,故本选项不符合题意;
B.既是轴对称图形又是中心对称图形,故本选项符合题意;
C.是轴对称图形,不是中心对称图形,故本选项不符合题意;
D.不是轴对称图形,是中心对称图形,故本选项不符合题意.
故选:B.
2.答案:B
解析:0.015毫米纳米纳米.
3.答案:D
解析:A.式子中两项不是同类项,不能合并,故A不符合题意;
B.,故B不符合题意;
C.,故C不符合题意;
D.,故D符合题意.
故选D.
4.答案:D
解析:排列得:81,82,82,83,85,86,89,92,
出现次数最多是82,即众数为82;
最中间的两个数为83和85,即中位数为84;
,即平均数为85;
,即方差为13.
故选:D.
5.答案:A
解析:,,
,
平分,
,
是的直径,
,
,
故选:A.
6.答案:A
解析:作轴,垂足为G,轴,垂足为H,
点A在函数图像上,点B在反比例函数图象上,
,,
,
,,
,
,
,
故选:A.
7.答案:2
解析:由题意得:,
解得:.
故答案为:2.
8.答案:
解析:
,
故答案为:.
9.答案:20
解析:设快马追上慢马需要x天,
根据题意,得,
解得,
故答案为:20.
10.答案:
解析:将该三角板绕点B顺时针旋转,使点C的对应点落在直线l上,
,即,
点A经过的路径长至少为.
故答案为:.
11.答案:4
解析:把点,点代入抛物线得,
,
解得,
抛物线,
令,得,
解得或,
,
;
故答案为:4.
12.答案:
解析:点A在直线上,且点A的横坐标为4,
点A的坐标为,
,
当点C在x轴上移动时,作与关于对称,且交x轴于点D,
由对称性质可知,,
当轴于点D时,最短,记此时点C所在位置为,
由对称性质可知,,
作于点E,有,
设,则,
,
,
解得,
经检验是方程的解,
,,
,
,
,
,
,
解得,
.
故答案为:.
13.答案:(1)1
(2)
解析:(1)原式
;
(2)原式
.
14.答案:(1)
(2)
解析:(1)3张相同的卡片上分别写有中国二十四节气中的“小满”、“芒种”、“夏至”的字样,
洗匀后,从中任意抽取1张卡片,抽到写有“小满”的卡片的概率,
故答案为:;
(2)把写有中国二十四节气中的“小满”、“芒种”、“夏至”3张卡片分别记为A、B、C,
画树状图如下:
共有6种等可能的结果,其中抽到一张写有“芒种”,一张写有“夏至”的卡片的结果有2种,
抽到一张写有“芒种”,一张写有“夏至”的卡片的概率为.
15.答案:(1)见解析
(2)见解析
解析:(1)证明:四边形是矩形,
,,
E是的中点,
,
在和中,
,
(2)证明:,
,
.
16.答案:(1)A,B两种商品每件进价各为100元,60元
(2)购进A商品的件数最多为20件
解析:(1)设A,B两种商品每件进价各为x元,y元,
由题意得,,
解得,
答:A,B两种商品每件进价各为100元,60元;
(2)设购进A商品的件数为m件,则购进B商品的件数为件,
由题意得,,
解得,
为整数,
的最大值为20,
答:购进A商品的件数最多为20件.
17.答案:(1)见详解
(2)
解析:(1)如下直线l即为所求.
(2)连接如下图:
为线段的垂直平分线,
,
,
,
为等腰直角三角形,
,
.
18.答案:(1)见解析
(2)
解析:(1)证明:四边形是平行四边形,
即,
,,
O为的中点,
,
,
,
,
四边形是平行四边形,
又,
四边形是菱形;
(2),,
,
平行四边形的周长为22,
菱形的周长为:
,
四边形是菱形,
,
又,
是等边三角形,
.
19.答案:(1)证明见解析
(2)6
解析:(1)证明:如图,连接OC,则,
.
点C是的中点,,
,
,.
,.
又为的半径,
是的切线.
(2)是的直径,
.
,
,.
,
.
20.答案:(1)
(2)电线塔的高度
解析:(1)斜坡的坡度,
,
,
,
,
;
(2)作于点F,则四边形是矩形,,,
设,
在中,,
,
在中,,
在中,,,
,
,
,
,
答:电线塔的高度.
21.答案:(1)50;30,6
(2)见解析
(3)
(4)人
解析:(1)本次调查活动随机抽取人数为(人),
,则,
,则,
故答案为:50;30,6;
(2)∵,
∴补全条形统计图如图所示:
(3)扇形统计图中“混动”类所在扇形的圆心角的度数为;
(4)(人).
答:估计喜欢新能源(纯电、混动、氢燃料)汽车的有3600人.
22.答案:(1),
(2)有最大值,此时
解析:(1),,
,
又,
,
,
点.
设直线的函数表达式为,将,代入得:
,解得:,
直线的函数表达式为.
将点代入,得.
,
将代入反比例函数解析式,
得:解得.
(2)延长交y轴于点Q,交于点L,
,,
,
,
,,
,
,
,
,
设点P的坐标为,则,,,
,
当时,有最大值,此时.
23.答案:问题背景:见解析
问题探究:见解析
问题拓展:
解析:问题背景:四边形是矩形,
,
E,F分别是,的中点
,
即,
;
问题探究:如图所示,取的中点H,连接,,
E是的中点,H是的中点,
,,
又,
,
,
,
四边形是平行四边形,
,
,
又,H是的中点,
,
,
,
;
问题拓展:如图所示,过点F作,则四边形是矩形,连接,
,
,
设,则,,
在中,,
,由(2)
,
又E是的中点,
垂直平分
,,
在,中,
,
,
设,则,
,
又,
,
,
又,
,
.
【满分120分 考试时间120分钟】
一、选择题(本大题共6小题,每小题3分,共18分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.[2024年辽宁中考真题]纹样是我国古代艺术中的瑰宝.下列四幅纹样图形既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.[2024年山东烟台中考真题]目前全球最薄的手撕钢产自中国,厚度只有0.015毫米,约是A4纸厚度的六分之一,已知1毫米百万纳米,0.015毫米等于多少纳米?将结果用科学记数法表示为( )
A.纳米 B.纳米 C.纳米 D.纳米
3.[2024年山东枣庄中考真题]下列运算正确的是( )
A. B.
C. D.
4.[2024年四川雅安中考真题]某校开展了红色经典故事演讲比赛,其中8名同学的成绩(单位:分)分别为:85,81,82,86,82,83,92,89.关于这组数据,下列说法中正确的是( )
A.众数是92 B.中位数是
C.平均数是84 D.方差是13
5.[2024年山东泰安中考真题]如图,AB是的直径,C,D是上两点,BA平分,若,则的度数为( )
A. B. C. D.
6.[2024年江苏苏州中考真题]如图,点A为反比例函数图象上的一点,连接,过点O作的垂线与反比例的图象交于点B,则的值为( )
A. B. C. D.
二、填空题(本大题共6小题,每小题3分,共18分.请把答案填在题中横线上)
7.[2024年湖南中考真题]若关于x的一元二次方程有两个相等的实数根,则k的值为________.
8.[2024年山东东营中考真题]因式分__________.
9.[2024年贵州中考真题]在元朝朱世杰所著的《算术启蒙》中,记载了一道题,大意是:快马每天行240里,慢马每天行150里,慢马先行12天,则快马追上慢马需要的天数是________.
10.[2024年吉林长春中考真题]一块含角的直角三角板按如图所示的方式摆放,边与直线l重合,.现将该三角板绕点B顺时针旋转,使点C的对应点落在直线l上,则点A经过的路径长至少为_________.(结果保留π)
11.[2024年辽宁中考真题]如图,在平面直角坐标系中,抛物线与x与相交于点A,B,点B的坐标为,若点在抛物线上,则的长为___________.
12.[2024年江苏宿迁中考真题]如图,在平面直角坐标系中,点A在直线上,且点A的横坐标为4,直角三角板的直角顶点C落在x轴上,一条直角边经过点A,另一条直角边与直线交于点B,当点C在x轴上移动时,线段的最小值为_________.
三、解答题(本大题共11小题,共84分.解答应写出必要的文字说明,证明过程或演算步骤)
13.(6分)[2024年江苏镇江中考真题](1)计算:;
(2)化简:.
14.(6分)[2024年江苏镇江中考真题]3张相同的卡片上分别写有中国二十四节气中的“小满”、“芒种”、“夏至”的字样,将卡片的背面朝上.
(1)洗匀后,从中任意抽取1张卡片,抽到写有“小满”的卡片的概率等于__________;
(2)洗匀后,从中任意抽取2张卡片,用画树状图或列表的方法,求抽到一张写有“芒种”,一张写有“夏至”的卡片的概率.
15.(6分)[2024年江苏无锡中考真题]如图,在矩形中,E是的中点,连接,.求证:
(1);
(2).
16.(6分)[2024年四川泸州中考真题]某商场购进A,B两种商品,已知购进3件A商品比购进4件B商品费用多60元;购进5件A商品和2件B商品总费用为620元.
(1)求A,B两种商品每件进价各为多少元?
(2)该商场计划购进A,B两种商品共60件,且购进B商品的件数不少于A商品件数的2倍.若A商品按每件150元销售,B商品按每件80元销售,为满足销售完A,B两种商品后获得的总利润不低于1770元,则购进A商品的件数最多为多少?
17.(6分)[2024年广西中考真题]如图,在中,,.
(1)尺规作图:作线段的垂直平分线l,分别交,于点D,E:(要求:保留作图痕迹,不写作法,标明字母)
(2)在(1)所作的图中,连接,若,求的长.
18.(8分)[2024年内蒙古中考真题]如图,在平行四边形中,点F在边上,,连接,点O为的中点,的延长线交边于点E,连接
(1)求证:四边形是菱形;
(2)若平行四边形的周长为22,,,求的长.
19.(8分)[2024年山东东营中考真题]如图,内接于,是的直径,点E在上,点C是的中点,,垂足为点D,DC的延长线交AB的延长线于点F.
(1)求证:CD是的切线;
(2)若,,求线段AF的长.
20.(8分)[2024年四川巴中中考真题]某兴趣小组开展了测量电线塔高度的实践活动.如图所示,斜坡的坡度,,在B处测得电线塔顶部D的仰角为,在E处测得电线塔顶部D的仰角为.
(1)求点B离水平地面的高度.
(2)求电线塔的高度(结果保留根号).
21.(9分)[2024年湖南长沙中考真题]中国新能源产业异军突起.中国车企在政策引导和支持下,瞄准纯电、混动和氢燃料等多元技术路线,加大研发投入形成了领先的技术优势,2023年,中国新能源汽车产销量均突破900万辆,连续9年位居全球第一.在某次汽车展览会上,工作人员随机抽取了部分参展人员进行了“我最喜欢的汽车类型”的调查活动(每人限选其中一种类型),并将数据整理后,绘制成下面有待完成的统计表、条形统计图和扇形统计图
类型 人数 百分比
纯电 m
混动 n
氢燃料 3
油车 5
请根据以上信息,解答下列问题:
(1)本次调查活动随机抽取了_____人;表中______,______;
(2)请补全条形统计图;
(3)请计算扇形统计图中“混动”类所在扇形的圆心角的度数;
(4)若此次汽车展览会的参展人员共有4000人,请你估计喜欢新能源(纯电、混动、氢燃料)汽车的有多少人?
22.(9分)[2024年江苏苏州中考真题]如图,中,,,,,反比例函数的图象与交于点,与交于点E.
(1)求m,k的值;
(2)点P为反比例函数图象上一动点(点P在D,E之间运动,不与D,E重合),过点P作,交y轴于点M,过点P作轴,交于点N,连接,求面积的最大值,并求出此时点P的坐标.
23.(12分)[2024年湖北武汉中考真题]问题背景:如图(1),在矩形中,点E,F分别是,的中点,连接,,求证:.
问题探究:如图(2),在四边形中,,,点E是的中点,点F在边上,,与交于点G,求证:.
问题拓展:如图(3),在“问题探究”的条件下,连接,,,直接写出的值.
参考答案
1.答案:B
解析:A、既不是轴对称图形也不是中心对称图形,故本选项不符合题意;
B.既是轴对称图形又是中心对称图形,故本选项符合题意;
C.是轴对称图形,不是中心对称图形,故本选项不符合题意;
D.不是轴对称图形,是中心对称图形,故本选项不符合题意.
故选:B.
2.答案:B
解析:0.015毫米纳米纳米.
3.答案:D
解析:A.式子中两项不是同类项,不能合并,故A不符合题意;
B.,故B不符合题意;
C.,故C不符合题意;
D.,故D符合题意.
故选D.
4.答案:D
解析:排列得:81,82,82,83,85,86,89,92,
出现次数最多是82,即众数为82;
最中间的两个数为83和85,即中位数为84;
,即平均数为85;
,即方差为13.
故选:D.
5.答案:A
解析:,,
,
平分,
,
是的直径,
,
,
故选:A.
6.答案:A
解析:作轴,垂足为G,轴,垂足为H,
点A在函数图像上,点B在反比例函数图象上,
,,
,
,,
,
,
,
故选:A.
7.答案:2
解析:由题意得:,
解得:.
故答案为:2.
8.答案:
解析:
,
故答案为:.
9.答案:20
解析:设快马追上慢马需要x天,
根据题意,得,
解得,
故答案为:20.
10.答案:
解析:将该三角板绕点B顺时针旋转,使点C的对应点落在直线l上,
,即,
点A经过的路径长至少为.
故答案为:.
11.答案:4
解析:把点,点代入抛物线得,
,
解得,
抛物线,
令,得,
解得或,
,
;
故答案为:4.
12.答案:
解析:点A在直线上,且点A的横坐标为4,
点A的坐标为,
,
当点C在x轴上移动时,作与关于对称,且交x轴于点D,
由对称性质可知,,
当轴于点D时,最短,记此时点C所在位置为,
由对称性质可知,,
作于点E,有,
设,则,
,
,
解得,
经检验是方程的解,
,,
,
,
,
,
,
解得,
.
故答案为:.
13.答案:(1)1
(2)
解析:(1)原式
;
(2)原式
.
14.答案:(1)
(2)
解析:(1)3张相同的卡片上分别写有中国二十四节气中的“小满”、“芒种”、“夏至”的字样,
洗匀后,从中任意抽取1张卡片,抽到写有“小满”的卡片的概率,
故答案为:;
(2)把写有中国二十四节气中的“小满”、“芒种”、“夏至”3张卡片分别记为A、B、C,
画树状图如下:
共有6种等可能的结果,其中抽到一张写有“芒种”,一张写有“夏至”的卡片的结果有2种,
抽到一张写有“芒种”,一张写有“夏至”的卡片的概率为.
15.答案:(1)见解析
(2)见解析
解析:(1)证明:四边形是矩形,
,,
E是的中点,
,
在和中,
,
(2)证明:,
,
.
16.答案:(1)A,B两种商品每件进价各为100元,60元
(2)购进A商品的件数最多为20件
解析:(1)设A,B两种商品每件进价各为x元,y元,
由题意得,,
解得,
答:A,B两种商品每件进价各为100元,60元;
(2)设购进A商品的件数为m件,则购进B商品的件数为件,
由题意得,,
解得,
为整数,
的最大值为20,
答:购进A商品的件数最多为20件.
17.答案:(1)见详解
(2)
解析:(1)如下直线l即为所求.
(2)连接如下图:
为线段的垂直平分线,
,
,
,
为等腰直角三角形,
,
.
18.答案:(1)见解析
(2)
解析:(1)证明:四边形是平行四边形,
即,
,,
O为的中点,
,
,
,
,
四边形是平行四边形,
又,
四边形是菱形;
(2),,
,
平行四边形的周长为22,
菱形的周长为:
,
四边形是菱形,
,
又,
是等边三角形,
.
19.答案:(1)证明见解析
(2)6
解析:(1)证明:如图,连接OC,则,
.
点C是的中点,,
,
,.
,.
又为的半径,
是的切线.
(2)是的直径,
.
,
,.
,
.
20.答案:(1)
(2)电线塔的高度
解析:(1)斜坡的坡度,
,
,
,
,
;
(2)作于点F,则四边形是矩形,,,
设,
在中,,
,
在中,,
在中,,,
,
,
,
,
答:电线塔的高度.
21.答案:(1)50;30,6
(2)见解析
(3)
(4)人
解析:(1)本次调查活动随机抽取人数为(人),
,则,
,则,
故答案为:50;30,6;
(2)∵,
∴补全条形统计图如图所示:
(3)扇形统计图中“混动”类所在扇形的圆心角的度数为;
(4)(人).
答:估计喜欢新能源(纯电、混动、氢燃料)汽车的有3600人.
22.答案:(1),
(2)有最大值,此时
解析:(1),,
,
又,
,
,
点.
设直线的函数表达式为,将,代入得:
,解得:,
直线的函数表达式为.
将点代入,得.
,
将代入反比例函数解析式,
得:解得.
(2)延长交y轴于点Q,交于点L,
,,
,
,
,,
,
,
,
,
设点P的坐标为,则,,,
,
当时,有最大值,此时.
23.答案:问题背景:见解析
问题探究:见解析
问题拓展:
解析:问题背景:四边形是矩形,
,
E,F分别是,的中点
,
即,
;
问题探究:如图所示,取的中点H,连接,,
E是的中点,H是的中点,
,,
又,
,
,
,
四边形是平行四边形,
,
,
又,H是的中点,
,
,
,
;
问题拓展:如图所示,过点F作,则四边形是矩形,连接,
,
,
设,则,,
在中,,
,由(2)
,
又E是的中点,
垂直平分
,,
在,中,
,
,
设,则,
,
又,
,
,
又,
,
.
同课章节目录
