2025届中考数学全真模拟卷 【甘肃专用】(含详解)
文档属性
| 名称 | 2025届中考数学全真模拟卷 【甘肃专用】(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-07 07:49:01 | ||
图片预览




文档简介
2025届中考数学全真模拟卷 【甘肃专用】
【满分120分 考试时间120分钟】
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
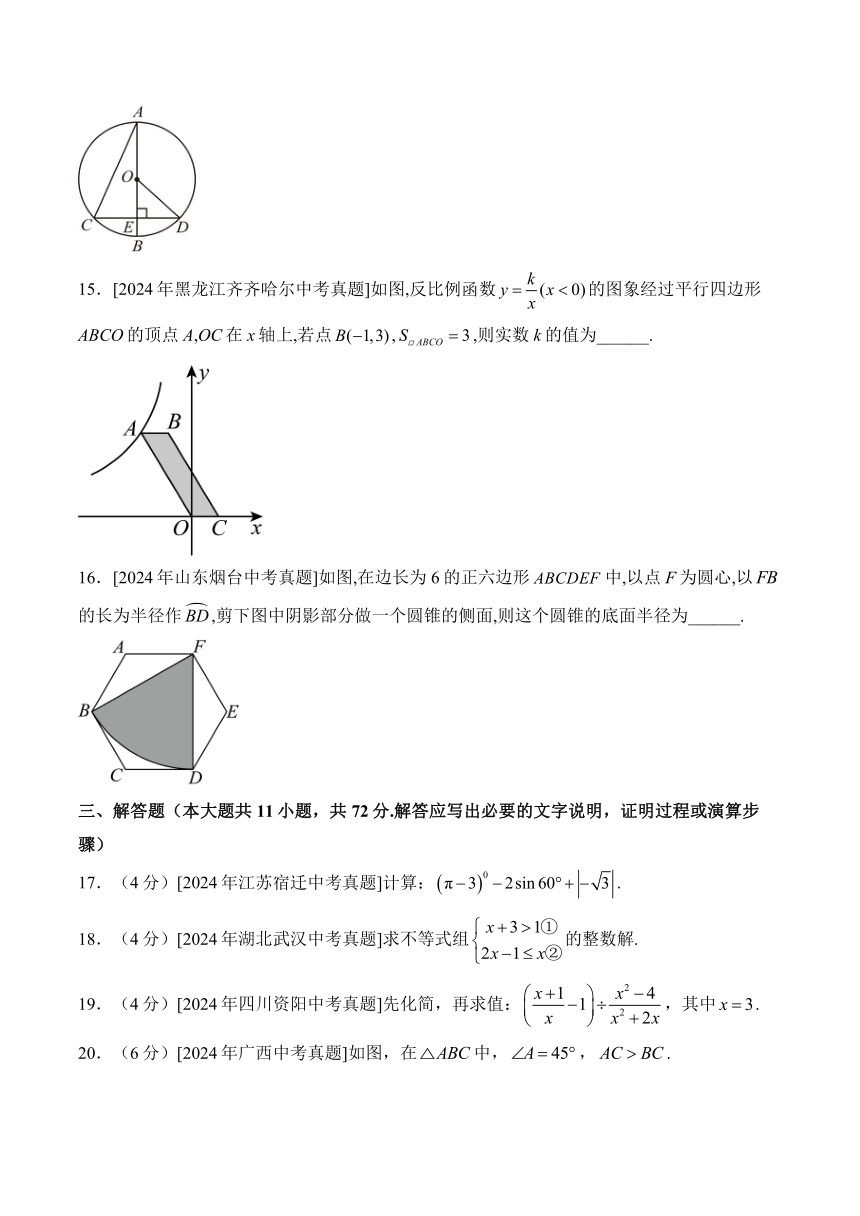
一、单选题
1.[2024年黑龙江齐齐哈尔中考真题]的相反数是( )
A.5 B.-5 C. D.
2.[2024年四川雅安中考真题]下列几何体中,主视图是三角形的是( )
A. B. C. D.
3.[2024年湖南长沙中考真题]我国近年来大力推进国家教育数字化战略行动,截至2024年6月上旬,上线慕课数量超过7.8万门,学习人次达1290000000建设和应用规模居世界第一.用科学记数法将数据1290000000表示为( )
A. B. C. D.
4.[2024年贵州中考真题]为培养青少年的科学态度和科学思维,某校创建了“科技创新”社团.小红将“科”“技”“创”“新”写在如图所示的方格纸中,若建立平面直角坐标系,使“创”“新”的坐标分别为,,则“技”所在的象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.[2024年山东泰安中考真题]如图,直线,等边三角形ABC的两个顶点B,C分别落在直线l,m上,若,则的度数是( )
A. B. C. D.
6.[2024年天津中考真题]若点,,都在反比例函数的图象上,则,,的大小关系是( )
A. B. C. D.
7.[2024年天津中考真题]《孙子算经》是我国古代著名的数学典籍,其中有一道题:“今有木,不知长短.引绳度之,余绳四尺五寸;屈绳度之,不足一尺.木长几何?”意思是:用一根绳子去量一根长木,绳子还剩余4.5尺;将绳子对折再量长木,长木还剩余1尺.问木长多少尺?设木长x尺,绳子长y尺,则可以列出的方程组为( )
A. B. C. D.
8.[2024年甘肃甘南州中考真题]如图,AB是⊙O的直径,DB,若,则的度数是( )
A.18° B.36° C.48° D.72°
9.[2024年辽宁中考真题]如图,在平面直角坐标系中,菱形的顶点A在x轴负半轴上,顶点B在直线上,若点B的横坐标是8,为点C的坐标为( )
A. B. C. D.
10.[2024年四川资阳中考真题]已知二次函数与的图像均过点和坐标原点O,这两个函数在时形成的封闭图像如图所示,P为线段的中点,过点P且与x轴不重合的直线与封闭图像交于B,C两点.给出下列结论:
①;
②;
③以O,A,B,C为顶点的四边形可以为正方形;
④若点B的横坐标为1,点Q在y轴上(Q,B,C三点不共线),则周长的最小值为.
其中,所有正确结论的个数是( )
A.1 B.2 C.3 D.4
二、填空题(本大题共6小题,每小题3分,共18分.请把答案填在题中横线上)
11.[2024年四川广安中考真题]分解因式:=________________.
12.[2024年山东烟台中考真题]若一元二次方程的两根为m,n,则的值为___________.
13.[2024年江苏宿迁中考真题]如图,在中,,是高,以点A为圆心,长为半径画弧,交于点E,再分别以B、E为圆心,大于的长为半径画弧,两弧在的内部交于点F,作射线,则_________.
14.[2024年黑龙江牡丹江中考真题]如图,在中,直径于点E,,,则弦的长为______.
15.[2024年黑龙江齐齐哈尔中考真题]如图,反比例函数的图象经过平行四边形ABCO的顶点A,OC在x轴上,若点,,则实数k的值为______.
16.[2024年山东烟台中考真题]如图,在边长为6的正六边形中,以点F为圆心,以的长为半径作,剪下图中阴影部分做一个圆锥的侧面,则这个圆锥的底面半径为______.
三、解答题(本大题共11小题,共72分.解答应写出必要的文字说明,证明过程或演算步骤)
17.(4分)[2024年江苏宿迁中考真题]计算:.
18.(4分)[2024年湖北武汉中考真题]求不等式组的整数解.
19.(4分)[2024年四川资阳中考真题]先化简,再求值:,其中.
20.(6分)[2024年广西中考真题]如图,在中,,.
(1)尺规作图:作线段的垂直平分线l,分别交,于点D,E:(要求:保留作图痕迹,不写作法,标明字母)
(2)在(1)所作的图中,连接,若,求的长.
21.(6分)[2024年江苏中考真题]在3张相同的小纸条上分别写有“石头”、“剪子”、“布”.将这3张小纸条做成3支签,放在不透明的盒子中搅匀.
(1)从盒子中任意抽出1支签,抽到“石头”的概率是________;
(2)甲、乙两人通过抽签分胜负,规定:“石头”胜“剪子”,“剪子”胜“布”,“布”胜“石头”.甲先从盒子中任意抽出1支签(不放回),乙再从余下的2支签中任意抽出1支签,求甲取胜的概率.
22.(8分)[2024年四川泸州中考真题]如图,海中有一个小岛C,某渔船在海中的A点测得小岛C位于东北方向上,该渔船由西向东航行一段时间后到达B点,测得小岛C位于北偏西方向上,再沿北偏东方向继续航行一段时间后到达D点,这时测得小岛C位于北偏西方向上.已知A,C相距30nmile.求C,D间的距离(计算过程中的数据不取近似值).
23.(7分)[2024年天津中考真题]为了解某校八年级学生每周参加科学教育的时间(单位:h),随机调查了该校八年级a名学生,根据统计的结果,绘制出如下的统计图①和图②.
请根据相关信息,解答下列问题:
(1)填空:a的值为______,图①中m的值为______,统计的这组学生每周参加科学教育的时间数据的众数和中位数分别为______和______;
(2)求统计的这组学生每周参加科学教育的时间数据的平均数;
(3)根据样本数据,若该校八年级共有学生500人,估计该校八年级学生每周参加科学教育的时间是的人数约为多少?
24.(7分)[2024年江苏淮安中考真题]如图,在平面直角坐标系中,一次函数的图像与x轴、y轴分别交于点A、B,与反比例函数的图像交于点C,已知点A坐标为,点C坐标为.
(1)求反比例函数及一次函数的表达式;
(2)点D在线段上,过点D且平行于x轴的直线交于点E,交反比例函数图像于点F,当时,求点F的坐标.
25.(8分)[2024年江西中考真题]如图,是半圆O的直径,点D是弦延长线上一点,连接,,.
(1)求证:是半圆O的切线;
(2)当时,求的长.
26.(8分)[2024年江苏中考真题]对于平面内有公共点的两个图形,若将其中一个图形沿着某个方向移动一定的距离d后与另一个图形重合,则称这两个图形存在“平移关联”,其中一个图形叫做另一个图形的“平移关联图形”.
(1)如图1,B、C、D是线段AE的四等分点.若,则在图中,线段AC的“平移关联图形”是________,________(写出符合条件的一种情况即可);
(2)如图2,等边三角形的边长是2.用直尺和圆规作出的一个“平移关联图形”,且满足(保留作图痕迹,不要求写作法);
(3)如图3,在平面直角坐标系中,点D、E、G的坐标分别是、、,以点G为圆心,r为半径画圆.若对上的任意点F,连接、、所形成的图形都存在“平移关联图形”,且满足,直接写出r的取值范围.
27.(10分)[2024年四川宜宾中考真题]如图,抛物线与x轴交于点和点B,与y轴交于点,其顶点为D.
(1)求抛物线的表达式及顶点D的坐标.
(2)在y轴上是否存在一点M,使得的周长最小.若存在,求出点M的坐标;若不存在,请说明理由.
(3)若点E在以点为圆心,1为半径的上,连接AE,以AE为边在AE的下方作等边三角形AEF,连接BF.求BF的取值范围.
参考答案
1.答案:C
解析:的相反数是.
故选:C.
2.答案:A
解析:A.主视图是三角形,故本选项符合题意;
B.主视图是矩形,故本选项不符合题意;
C.主视图是矩形,故本选项不符合题意;
D.主视图是正方形,故本选项不符合题意.
故选:A.
3.答案:C
解析:用科学记数法将数据1290000000表示为,
故选:C.
4.答案:A
解析:如图建立直角坐标系,则“技”在第一象限,
故选A.
5.答案:B
解析:如图,过点A作.因为直线,所以.
因为是等边三角形,所以.
因为,所以,所以.
因为,所以.
6.答案:B
解析:,
反比例函数的图象分布在第一、三象限,在每个象限内,y随x的增大而减小,
点,,都在反比例函数的图象上,
点分布在第三象限,,分布在第一象限,且,
,,
,
故选:B.
7.答案:A
解析:用绳子去量长木,绳子还剩余4.5尺,
,
将绳子对折再量长木,长木还剩余1尺,
,
.根据题意可列方程组.
故选:A.
8.答案:B
解析:连接,
、分别切于点B、C,
是的直径
,
,
,
故选:B.
9.答案:B
解析:过点B作轴,垂足为点D,
顶点B在直线上,点B的横坐标是8,
,即,
,
轴,
由勾股定理得:,
四边形是菱形,
,轴,
将点B向左平移10个单位得到点C,点,
故选:B.
10.答案:D
解析:①二次函数与的图像均过点和坐标原点O,P为线段的中点,
,两个函数的对称轴均为直线,
即,
解得:,故①正确;
②如图,过点B作交x轴于点D,过点C作交x轴于点E,
,
由函数的对称性可知,
在和中,
,
,
,故正确②;
③当点B、C分别在两个函数的顶点上时,,点B、C的横坐标均为2,
由①可知两个函数的解析式分别为,,
,,
,
点,,,
由,
此时以O,A,B,C为顶点的四边形为正方形,故③正确;
④作点B关于y轴的对称点,连接交y轴于点Q,此时周长的最小,最小值为,
点B的横坐标为1,
,点C的横坐标为3,
,,
,,
周长的最小值为,故正确④;
故选:D.
11.答案:
解析:.
12.答案:6
解析:一元二次方程的两根为m,n,
,,,.
13.答案:
解析:因为,,
所以,
根据题意得:平分,
所以,
因为为高,
所以,
所以,
所以,
故答案为:.
14.答案:
解析:,,
,
设的半径为r,则,
在中,由勾股定理得:,即,
解得:,
,,
,
在中,由勾股定理得:,
故答案为:.
15.答案:-6
解析:如图,延长交y轴于点D,
,
,
,
是平行四边形,
,
,
,
点A在反比例函数图象上,
.
故答案为:.
16.答案:
解析:∵正六边形,
∴,,
∴,,
∴,
过点A作于点G,则:,
设圆锥的底面圆的半径为r,则:,
∴;
故答案为:.
17.答案:1
解析:
.
18.答案:整数解为:-1,0,1
解析:
解不等式①得:
解不等式②得:
不等式组的解集为:,
整数解为:-1,0,1.
19.答案:;1
解析:
,
把代入得:原式.
20.答案:(1)见详解
(2)
解析:(1)如下直线l即为所求.
(2)连接如下图:
为线段的垂直平分线,
,
,
,
为等腰直角三角形,
,
.
21.答案:(1)
(2)
解析:(1)一共有3支签,写有“石头”的签有1支,且每支签被抽到的概率相同,
从盒子中任意抽出1支签,抽到“石头”的概率是,
故答案为:;
(2)设分别用A、B、C表示“石头”、“剪子”、“布”,列表如下:
甲乙 A B C
A
B
C
由表格可知,一共有6种等可能性的结果数,其中甲获胜的结果数有,,,共3种,
甲获胜的概率为.
22.答案:C,D间的距离为
解析:作于点E,
由题意得,,,
是等腰直角三角形,
,
,
在中,,
在中,,,
在中,,
答:C,D间的距离为.
23.答案:(1)50,34,8,8
(2)8.36
(3)150人
解析:(1)(人,
,
,
在这组数据中,8出现了17次,次数最多,
众数是8,
将这组数据从小到大依次排列,处于最中间的第25,26名学生的分数都是8,
中位数是,
故答案为:50,34,8,8.
(2)
这组数据的平均数是8.36.
(3)在所抽取的样本中,每周参加科学教育的时间是的学生占,
根据样本数据,估计该校八年级学生500人中,每周参加科学教育的时间是的学生占,有.
估计该校八年级学生每周参加科学教育的时间是的人数约为150.
24.答案:(1)
(2)
解析:(1)把点代入得:,
解得,
反比例函数的表达式为,
把点,点代入得,
,
解得,
一次函数的表达式为;
(2)设,
平行于x轴,
,
,
,
,
解得,
,
点F的纵坐标为,
把代入得,,
点F的坐标为.
25.答案:(1)见解析
(2)
解析:(1)证明:是半圆O的直径,
,
,
,
,
是半圆O的切线;
(2)如图,连接,
,,
为等边三角形,
,,
,
.
26.答案:(1),2
(2)图见解析(答案不唯一)
(3)或
解析:(1)B、C、D是线段AE的四等分点.,
,
,
线段的平移图形是,;
故答案为:,2;
(2)如图:即为所求;
由作图可知:,
四边形为菱形,
,
,
四边形为菱形,
,
即为所求;
(3)点D、E、G的坐标分别是、、,
,,
,,
对上的任意点F,连接、、所形成的图形都存在“平移关联图形”,且满足,且,
,,
当在圆外时,
,,
,
,
.
当在圆内时,
则:,
,
;
综上:或.
27.答案:(1)表达式为;顶点D的坐标为
(2)存在,点M的坐标为
(3)
解析:(1)把,的坐标分别代入,得
解得
抛物线的表达式为.
,
抛物线的顶点D的坐标为.
(2)存在.
作点关于y轴的对称点,则,连接,,如图(1).
在中,令,得,
解得,,
.
的长为定值,
要使的周长最小,只要最小即可.
,
,
当点B,M,共线时,最小,最小值为的长,
此时的周长也最小.
设直线的函数表达式为,
将,的坐标分别代入,
得解得
直线的函数表达式为.
令,得,
当的周长最小时,点M的坐标为.
(3)以AP为边,在AP下方作等边三角形APQ,连接PE,QF,BQ,如图(2).
由,,是等边三角形,可得点Q的坐标为.
,是等边三角形,
,,,
,
,
,
点F在以为圆心,1为半径的圆上.
,.
当F在线段BQ与的交点处时,BF最小,此时.
当F在BQ的延长线与的交点处时,BF最大,此时.
综上,BF的取值范围是.
【满分120分 考试时间120分钟】
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
一、单选题
1.[2024年黑龙江齐齐哈尔中考真题]的相反数是( )
A.5 B.-5 C. D.
2.[2024年四川雅安中考真题]下列几何体中,主视图是三角形的是( )
A. B. C. D.
3.[2024年湖南长沙中考真题]我国近年来大力推进国家教育数字化战略行动,截至2024年6月上旬,上线慕课数量超过7.8万门,学习人次达1290000000建设和应用规模居世界第一.用科学记数法将数据1290000000表示为( )
A. B. C. D.
4.[2024年贵州中考真题]为培养青少年的科学态度和科学思维,某校创建了“科技创新”社团.小红将“科”“技”“创”“新”写在如图所示的方格纸中,若建立平面直角坐标系,使“创”“新”的坐标分别为,,则“技”所在的象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.[2024年山东泰安中考真题]如图,直线,等边三角形ABC的两个顶点B,C分别落在直线l,m上,若,则的度数是( )
A. B. C. D.
6.[2024年天津中考真题]若点,,都在反比例函数的图象上,则,,的大小关系是( )
A. B. C. D.
7.[2024年天津中考真题]《孙子算经》是我国古代著名的数学典籍,其中有一道题:“今有木,不知长短.引绳度之,余绳四尺五寸;屈绳度之,不足一尺.木长几何?”意思是:用一根绳子去量一根长木,绳子还剩余4.5尺;将绳子对折再量长木,长木还剩余1尺.问木长多少尺?设木长x尺,绳子长y尺,则可以列出的方程组为( )
A. B. C. D.
8.[2024年甘肃甘南州中考真题]如图,AB是⊙O的直径,DB,若,则的度数是( )
A.18° B.36° C.48° D.72°
9.[2024年辽宁中考真题]如图,在平面直角坐标系中,菱形的顶点A在x轴负半轴上,顶点B在直线上,若点B的横坐标是8,为点C的坐标为( )
A. B. C. D.
10.[2024年四川资阳中考真题]已知二次函数与的图像均过点和坐标原点O,这两个函数在时形成的封闭图像如图所示,P为线段的中点,过点P且与x轴不重合的直线与封闭图像交于B,C两点.给出下列结论:
①;
②;
③以O,A,B,C为顶点的四边形可以为正方形;
④若点B的横坐标为1,点Q在y轴上(Q,B,C三点不共线),则周长的最小值为.
其中,所有正确结论的个数是( )
A.1 B.2 C.3 D.4
二、填空题(本大题共6小题,每小题3分,共18分.请把答案填在题中横线上)
11.[2024年四川广安中考真题]分解因式:=________________.
12.[2024年山东烟台中考真题]若一元二次方程的两根为m,n,则的值为___________.
13.[2024年江苏宿迁中考真题]如图,在中,,是高,以点A为圆心,长为半径画弧,交于点E,再分别以B、E为圆心,大于的长为半径画弧,两弧在的内部交于点F,作射线,则_________.
14.[2024年黑龙江牡丹江中考真题]如图,在中,直径于点E,,,则弦的长为______.
15.[2024年黑龙江齐齐哈尔中考真题]如图,反比例函数的图象经过平行四边形ABCO的顶点A,OC在x轴上,若点,,则实数k的值为______.
16.[2024年山东烟台中考真题]如图,在边长为6的正六边形中,以点F为圆心,以的长为半径作,剪下图中阴影部分做一个圆锥的侧面,则这个圆锥的底面半径为______.
三、解答题(本大题共11小题,共72分.解答应写出必要的文字说明,证明过程或演算步骤)
17.(4分)[2024年江苏宿迁中考真题]计算:.
18.(4分)[2024年湖北武汉中考真题]求不等式组的整数解.
19.(4分)[2024年四川资阳中考真题]先化简,再求值:,其中.
20.(6分)[2024年广西中考真题]如图,在中,,.
(1)尺规作图:作线段的垂直平分线l,分别交,于点D,E:(要求:保留作图痕迹,不写作法,标明字母)
(2)在(1)所作的图中,连接,若,求的长.
21.(6分)[2024年江苏中考真题]在3张相同的小纸条上分别写有“石头”、“剪子”、“布”.将这3张小纸条做成3支签,放在不透明的盒子中搅匀.
(1)从盒子中任意抽出1支签,抽到“石头”的概率是________;
(2)甲、乙两人通过抽签分胜负,规定:“石头”胜“剪子”,“剪子”胜“布”,“布”胜“石头”.甲先从盒子中任意抽出1支签(不放回),乙再从余下的2支签中任意抽出1支签,求甲取胜的概率.
22.(8分)[2024年四川泸州中考真题]如图,海中有一个小岛C,某渔船在海中的A点测得小岛C位于东北方向上,该渔船由西向东航行一段时间后到达B点,测得小岛C位于北偏西方向上,再沿北偏东方向继续航行一段时间后到达D点,这时测得小岛C位于北偏西方向上.已知A,C相距30nmile.求C,D间的距离(计算过程中的数据不取近似值).
23.(7分)[2024年天津中考真题]为了解某校八年级学生每周参加科学教育的时间(单位:h),随机调查了该校八年级a名学生,根据统计的结果,绘制出如下的统计图①和图②.
请根据相关信息,解答下列问题:
(1)填空:a的值为______,图①中m的值为______,统计的这组学生每周参加科学教育的时间数据的众数和中位数分别为______和______;
(2)求统计的这组学生每周参加科学教育的时间数据的平均数;
(3)根据样本数据,若该校八年级共有学生500人,估计该校八年级学生每周参加科学教育的时间是的人数约为多少?
24.(7分)[2024年江苏淮安中考真题]如图,在平面直角坐标系中,一次函数的图像与x轴、y轴分别交于点A、B,与反比例函数的图像交于点C,已知点A坐标为,点C坐标为.
(1)求反比例函数及一次函数的表达式;
(2)点D在线段上,过点D且平行于x轴的直线交于点E,交反比例函数图像于点F,当时,求点F的坐标.
25.(8分)[2024年江西中考真题]如图,是半圆O的直径,点D是弦延长线上一点,连接,,.
(1)求证:是半圆O的切线;
(2)当时,求的长.
26.(8分)[2024年江苏中考真题]对于平面内有公共点的两个图形,若将其中一个图形沿着某个方向移动一定的距离d后与另一个图形重合,则称这两个图形存在“平移关联”,其中一个图形叫做另一个图形的“平移关联图形”.
(1)如图1,B、C、D是线段AE的四等分点.若,则在图中,线段AC的“平移关联图形”是________,________(写出符合条件的一种情况即可);
(2)如图2,等边三角形的边长是2.用直尺和圆规作出的一个“平移关联图形”,且满足(保留作图痕迹,不要求写作法);
(3)如图3,在平面直角坐标系中,点D、E、G的坐标分别是、、,以点G为圆心,r为半径画圆.若对上的任意点F,连接、、所形成的图形都存在“平移关联图形”,且满足,直接写出r的取值范围.
27.(10分)[2024年四川宜宾中考真题]如图,抛物线与x轴交于点和点B,与y轴交于点,其顶点为D.
(1)求抛物线的表达式及顶点D的坐标.
(2)在y轴上是否存在一点M,使得的周长最小.若存在,求出点M的坐标;若不存在,请说明理由.
(3)若点E在以点为圆心,1为半径的上,连接AE,以AE为边在AE的下方作等边三角形AEF,连接BF.求BF的取值范围.
参考答案
1.答案:C
解析:的相反数是.
故选:C.
2.答案:A
解析:A.主视图是三角形,故本选项符合题意;
B.主视图是矩形,故本选项不符合题意;
C.主视图是矩形,故本选项不符合题意;
D.主视图是正方形,故本选项不符合题意.
故选:A.
3.答案:C
解析:用科学记数法将数据1290000000表示为,
故选:C.
4.答案:A
解析:如图建立直角坐标系,则“技”在第一象限,
故选A.
5.答案:B
解析:如图,过点A作.因为直线,所以.
因为是等边三角形,所以.
因为,所以,所以.
因为,所以.
6.答案:B
解析:,
反比例函数的图象分布在第一、三象限,在每个象限内,y随x的增大而减小,
点,,都在反比例函数的图象上,
点分布在第三象限,,分布在第一象限,且,
,,
,
故选:B.
7.答案:A
解析:用绳子去量长木,绳子还剩余4.5尺,
,
将绳子对折再量长木,长木还剩余1尺,
,
.根据题意可列方程组.
故选:A.
8.答案:B
解析:连接,
、分别切于点B、C,
是的直径
,
,
,
故选:B.
9.答案:B
解析:过点B作轴,垂足为点D,
顶点B在直线上,点B的横坐标是8,
,即,
,
轴,
由勾股定理得:,
四边形是菱形,
,轴,
将点B向左平移10个单位得到点C,点,
故选:B.
10.答案:D
解析:①二次函数与的图像均过点和坐标原点O,P为线段的中点,
,两个函数的对称轴均为直线,
即,
解得:,故①正确;
②如图,过点B作交x轴于点D,过点C作交x轴于点E,
,
由函数的对称性可知,
在和中,
,
,
,故正确②;
③当点B、C分别在两个函数的顶点上时,,点B、C的横坐标均为2,
由①可知两个函数的解析式分别为,,
,,
,
点,,,
由,
此时以O,A,B,C为顶点的四边形为正方形,故③正确;
④作点B关于y轴的对称点,连接交y轴于点Q,此时周长的最小,最小值为,
点B的横坐标为1,
,点C的横坐标为3,
,,
,,
周长的最小值为,故正确④;
故选:D.
11.答案:
解析:.
12.答案:6
解析:一元二次方程的两根为m,n,
,,,.
13.答案:
解析:因为,,
所以,
根据题意得:平分,
所以,
因为为高,
所以,
所以,
所以,
故答案为:.
14.答案:
解析:,,
,
设的半径为r,则,
在中,由勾股定理得:,即,
解得:,
,,
,
在中,由勾股定理得:,
故答案为:.
15.答案:-6
解析:如图,延长交y轴于点D,
,
,
,
是平行四边形,
,
,
,
点A在反比例函数图象上,
.
故答案为:.
16.答案:
解析:∵正六边形,
∴,,
∴,,
∴,
过点A作于点G,则:,
设圆锥的底面圆的半径为r,则:,
∴;
故答案为:.
17.答案:1
解析:
.
18.答案:整数解为:-1,0,1
解析:
解不等式①得:
解不等式②得:
不等式组的解集为:,
整数解为:-1,0,1.
19.答案:;1
解析:
,
把代入得:原式.
20.答案:(1)见详解
(2)
解析:(1)如下直线l即为所求.
(2)连接如下图:
为线段的垂直平分线,
,
,
,
为等腰直角三角形,
,
.
21.答案:(1)
(2)
解析:(1)一共有3支签,写有“石头”的签有1支,且每支签被抽到的概率相同,
从盒子中任意抽出1支签,抽到“石头”的概率是,
故答案为:;
(2)设分别用A、B、C表示“石头”、“剪子”、“布”,列表如下:
甲乙 A B C
A
B
C
由表格可知,一共有6种等可能性的结果数,其中甲获胜的结果数有,,,共3种,
甲获胜的概率为.
22.答案:C,D间的距离为
解析:作于点E,
由题意得,,,
是等腰直角三角形,
,
,
在中,,
在中,,,
在中,,
答:C,D间的距离为.
23.答案:(1)50,34,8,8
(2)8.36
(3)150人
解析:(1)(人,
,
,
在这组数据中,8出现了17次,次数最多,
众数是8,
将这组数据从小到大依次排列,处于最中间的第25,26名学生的分数都是8,
中位数是,
故答案为:50,34,8,8.
(2)
这组数据的平均数是8.36.
(3)在所抽取的样本中,每周参加科学教育的时间是的学生占,
根据样本数据,估计该校八年级学生500人中,每周参加科学教育的时间是的学生占,有.
估计该校八年级学生每周参加科学教育的时间是的人数约为150.
24.答案:(1)
(2)
解析:(1)把点代入得:,
解得,
反比例函数的表达式为,
把点,点代入得,
,
解得,
一次函数的表达式为;
(2)设,
平行于x轴,
,
,
,
,
解得,
,
点F的纵坐标为,
把代入得,,
点F的坐标为.
25.答案:(1)见解析
(2)
解析:(1)证明:是半圆O的直径,
,
,
,
,
是半圆O的切线;
(2)如图,连接,
,,
为等边三角形,
,,
,
.
26.答案:(1),2
(2)图见解析(答案不唯一)
(3)或
解析:(1)B、C、D是线段AE的四等分点.,
,
,
线段的平移图形是,;
故答案为:,2;
(2)如图:即为所求;
由作图可知:,
四边形为菱形,
,
,
四边形为菱形,
,
即为所求;
(3)点D、E、G的坐标分别是、、,
,,
,,
对上的任意点F,连接、、所形成的图形都存在“平移关联图形”,且满足,且,
,,
当在圆外时,
,,
,
,
.
当在圆内时,
则:,
,
;
综上:或.
27.答案:(1)表达式为;顶点D的坐标为
(2)存在,点M的坐标为
(3)
解析:(1)把,的坐标分别代入,得
解得
抛物线的表达式为.
,
抛物线的顶点D的坐标为.
(2)存在.
作点关于y轴的对称点,则,连接,,如图(1).
在中,令,得,
解得,,
.
的长为定值,
要使的周长最小,只要最小即可.
,
,
当点B,M,共线时,最小,最小值为的长,
此时的周长也最小.
设直线的函数表达式为,
将,的坐标分别代入,
得解得
直线的函数表达式为.
令,得,
当的周长最小时,点M的坐标为.
(3)以AP为边,在AP下方作等边三角形APQ,连接PE,QF,BQ,如图(2).
由,,是等边三角形,可得点Q的坐标为.
,是等边三角形,
,,,
,
,
,
点F在以为圆心,1为半径的圆上.
,.
当F在线段BQ与的交点处时,BF最小,此时.
当F在BQ的延长线与的交点处时,BF最大,此时.
综上,BF的取值范围是.
同课章节目录
