2025届中考数学全真模拟卷 【重庆专用】(含详解)
文档属性
| 名称 | 2025届中考数学全真模拟卷 【重庆专用】(含详解) | 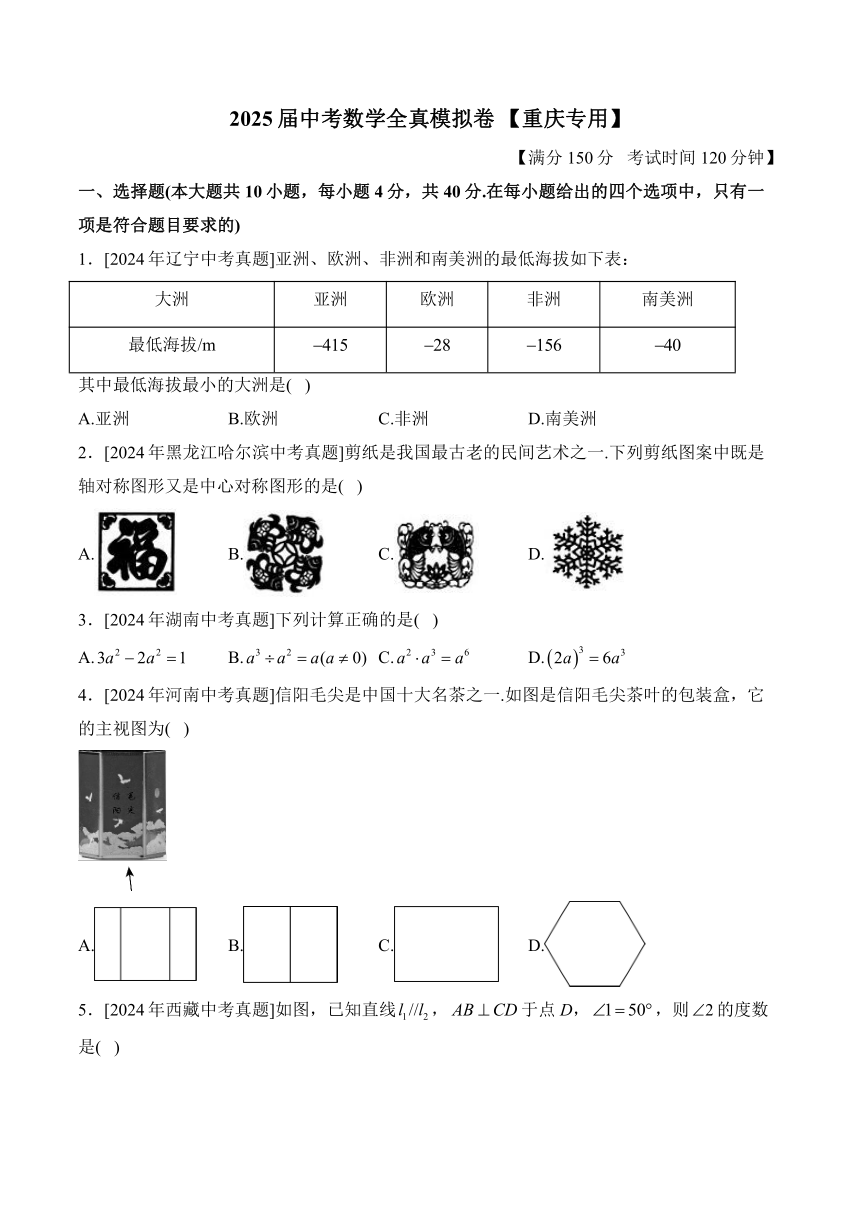 | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-07 08:45:17 | ||
图片预览





文档简介
2025届中考数学全真模拟卷 【重庆专用】
【满分150分 考试时间120分钟】
一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.[2024年辽宁中考真题]亚洲、欧洲、非洲和南美洲的最低海拔如下表:
大洲 亚洲 欧洲 非洲 南美洲
最低海拔/m
其中最低海拔最小的大洲是( )
A.亚洲 B.欧洲 C.非洲 D.南美洲
2.[2024年黑龙江哈尔滨中考真题]剪纸是我国最古老的民间艺术之一.下列剪纸图案中既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3.[2024年湖南中考真题]下列计算正确的是( )
A. B. C. D.
4.[2024年河南中考真题]信阳毛尖是中国十大名茶之一.如图是信阳毛尖茶叶的包装盒,它的主视图为( )
A. B. C. D.
5.[2024年西藏中考真题]如图,已知直线,于点D,,则的度数是( )
A. B. C. D.
6.[2024年重庆中考真题]已知,则实数m的范围是( )
A. B. C. D.
7.[2024年江苏宿迁中考真题]规定:对于任意实数a、b、c,有,其中等式右面是通常的乘法和加法运算,如.若关于x的方程有两个不相等的实数根,则m的取值范围为( )
A. B. C.且 D.且
8.[2024年黑龙江牡丹江中考真题]如图是由一些同样大小的三角形按照一定规律所组成的图形,第1个图有4个三角形.第2个图有7个三角形,第3个图有10个三角形……按照此规律排列下去,第674个图中三角形的个数是( )
A.2022 B.2023 C.2024 D.2025
9.[2024年河南中考真题]如图,是边长为的等边三角形的外接圆,点D是的中点,连接,.以点D为圆心,的长为半径在内画弧,则阴影部分的面积为( )
A. B. C. D.
10.[2024年浙江中考真题]如图,在中,,相交于点O,,.过点A作的垂线交于点E,记长为x,长为y.当x,y的值发生变化时,下列代数式的值不变的是( )
A. B. C. D.
二、填空题(本大题共6小题,每小题4分,共24分.请把答案填在题中横线上)
11.[2024年甘肃甘南州中考真题]若分式的值为0,则x的值为______.
12.[2024年江苏苏州中考真题]如图,正八边形转盘被分成八个面积相等的三角形,任意转动这个转盘一次,当转盘停止转动时,指针落在阴影部分的概率是______.
13.[2024年山东烟台中考真题]若一元二次方程的两根为m,n,则的值为___________.
14.[2024年四川巴中中考真题]如图,四边形ABCD是的内接四边形,若四边形OABC为菱形,则的度数是__________.
15.[2024年重庆中考真题]若关于x的不等式组至少有2个整数解,且关于y的分式方程的解为非负整数,则所有满足条件的整数a的值之和为______.
16.[2024年四川宜宾中考真题]如图,正方形的边长为1,M、N是边、上的动点.若,则的最小值为__________.
三、解答题(本大题共9小题,共86分.解答应写出必要的文字说明,证明过程或演算步骤)
17.(8分)[2024年内蒙古中考真题]计算:.
18.(8分)[2024年江苏宿迁中考真题]先化简再求值:,其中.
19.(10分)[2024年广西中考真题]如图,在中,,.
(1)尺规作图:作线段的垂直平分线l,分别交,于点D,E:(要求:保留作图痕迹,不写作法,标明字母)
(2)在(1)所作的图中,连接,若,求的长.
20.(10分)[2024年陕西中考真题]水资源问题是全球关注的热点,节约用水已成为全民共识.某校课外兴趣小组想了解居民家庭用水情况,他们从一小区随机抽取了30户家庭,收集了这30户家庭去年7月份的用水量,并对这30个数据进行整理,绘制了如下统计图表:
组别 用水量 组内平均数
A
B
C
D
根据以上信息,解答下列问:
(1)这30个数据的中位数落在________组(填组别);
(2)求这30户家庭去年7月份的总用水量;
(3)该小区有1000户家庭,若每户家庭今年7月份的用水量都比去年7月份各自家庭的用水量节约,请估计这1000户家庭今年7月份的总用水量比去年7月份的总用水量节约多少
21.(10分)为培养学生的创新意识,提高学生的动手能力,某校计划购买一批航空、航海模型,已知商场某品牌航空模型的单价比航海模型的单价多35元,用2000元购买航空模型的数量是用1800元购买航海模型数量的.
(1)求航空和航海模型的单价;
(2)学校采购时恰逢该商场“六一儿童节”促销:航空模型八折优惠.若购买航空、航海模型共120个,且航空模型数量不少于航海模型数量的,请问分别购买多少个航空和航海模型,学校花费最少?
22.(10分)[2024年河南中考真题]如图,矩形的四个顶点都在格点(网格线的交点)上,对角线,相交于点E,反比例函数的图象经过点A.
(1)求这个反比例函数的表达式.
(2)请先描出这个反比例函数图象上不同于点A的三个格点,再画出反比例函数的图象.
(3)将矩形向左平移,当点E落在这个反比例函数的图象上时,平移的距离为________.
23.(10分)[2024年天津中考真题]综合与实践活动中,要用测角仪测量天津海河上一座桥的桥塔的高度(如图①).某学习小组设计了一个方案:如图②,点C,D,E依次在同一条水平直线上,,,垂足为C.在D处测得桥塔顶部B的仰角()为,测得桥塔底部A的俯角()为,又在E处测得桥塔顶部B的仰角()为.
(1)求线段的长(结果取整数);
(2)求桥塔的高度(结果取整数).
参考数据:,.
24.(10分)[2024年山东东营中考真题]如图,在平面直角坐标系中,已知抛物线与x轴交于,两点,与y轴交于点C,点D是抛物线上的一个动点.
(1)求抛物线的表达式;
(2)当点D在直线BC下方的抛物线上时,过点D作y轴的平行线交BC于点E,设点D的横坐标为t,DE的长为l,请写出l关于t的函数表达式,并写出自变量t的取值范围;
(3)在(2)的条件下,连接AD,交BC于点F,求的最大值.
25.(10分)[2024年甘肃甘南州中考真题]某学校数学兴趣小组在数学课外活动中,对多边形内两条互相垂直的线段做了如下探究:
(1)如图1,在正方形中,点E,F分别是,上的两点,连接,,且,猜想并计算的值;
(2)如图2,在矩形中,,点E是上的一点,连接,,且,求的值;
(3)如图3,在四边形中,,点E为上一点,连接,过点C作的垂线交的延长线于点G,交的延长线于点F,求证:.
参考答案
1.答案:A
解析:,,,,
,
,
海拔最低的是亚洲.
故选:A.
2.答案:D
解析:A.图形既不是轴对称图形,也不是中心对称图形,故此选项不符合题意;
B.图形是中心对称图形,但不是轴对称图形,故此选项不合题意;
C.图形是轴对称图形,但不是中心对称图形,故此选项不合题意;
D.图形既是轴对称图形又是中心对称图形,故此选项符合题意.
故选:D.
3.答案:B
解析:A、,故该选项不正确,不符合题意;
B、,故该选项正确,符合题意;
C、,故该选项不正确,不符合题意;
D、,故该选项不正确,不符合题意;
故选:B.
4.答案:A
解析:这个茶叶盒的主视图为:
故选:A.
5.答案:A
解析:∵,,
∴,
∵,
∴,
∴,故A正确.
故选:A.
6.答案:B
解析:,
,
,
故选:B.
7.答案:D
解析:,
,即,
关于x的方程有两个不相等的实数根,
,且,
解得且,
故选:D.
8.答案:B
解析:第1个图案有4个三角形,即,
第2个图案有7个三角形,即,
第3个图案有10个三角形,即,
…,
按此规律摆下去,第n个图案有个三角形,
则第674个图案中三角形的个数为:(个).
故选:B.
9.答案:C
解析:如图,连接、、,交于点H,
为等边三角形,
,
,,
是弧的中点,
,,,
,
,,
为等边三角形,
,
,
故选:C.
10.答案:C
解析:过点D作交的延长线于点F,
的垂线交于点E,
,
四边形是平行四边形,
,,
,
,,
由勾股定理可得,,
,
,
即,解得,
当x,y的值发生变化时,代数式的值不变的是,
故选:C.
11.答案:-2
解析:分式的值为0,
解得:,
故答案为:-2.
12.答案:
解析:根据题意可知,正八边形转盘被分成八个面积相等的三角形,
其中阴影部分的面积为3个面积相等的三角形,
指针落在阴影部分的概率等于阴影部分的面积除以正八边形的面积,即,
故答案为:.
13.答案:6
解析:一元二次方程的两根为m,n,
,,,.
14.答案:
解析:四边形OABC为菱形,
,
由圆周角定理得:,
四边形ABCD为的内接四边形,
,
,解得:,
故答案为:.
15.答案:16
解析:,
解①得:,
解②得:,
关于x的一元一次不等式组至少有两个整数解,
,
解得,
解方程,得,
关于y的分式方程的解为非负整数,
且,是偶数,
解得且,a是偶数,
且,a是偶数,
则所有满足条件的整数a的值之和是,
故答案为:16.
16.答案:/
解析:正方形的边长为1,
,,
将顺时针旋转得到,则,
,,,,
点P、B、M、C共线,
,
,
,,,
,
,
,
设,,则,,
,
∵,
,即,
整理得:,
,
当且仅当,即,也即时,取最小值,
故答案为:.
17.答案:11
解析:
.
18.答案:,
解析:
,
当时,原式.
19.答案:(1)见详解
(2)
解析:(1)如下直线l即为所求.
(2)连接如下图:
为线段的垂直平分线,
,
,
,
为等腰直角三角形,
,
.
20.答案:(1)B
(2)
(3)
解析:(1)根据条形统计图可知:组有10户,B组有12户,C组有6户,D组有2户,
将30个数据从小到大进行排序,排在第15和16的两个数据一定落在B组,
这30个数据的中位数落在B组;
(2)这30户家庭去年7月份的总用水量为:
;
(3)去年每户家庭7月份的用水量约为:,
每户家庭今年7月份的用水量都比去年7月份各自家庭的用水量节约,
今年每户家庭7月份的节约用水量约为:,
估计这1000户家庭今年7月份的总用水量比去年7月份的总用水量节约:
.
21.答案:(1)航空模型的单价为125元,航海模型的单价为90元
(2)购买航空模型40个,航海模型80个,学校花费最少
解析:(1)设航空模型的单价为x元,则航海模型的单价为元,
根据题意,得,
解得,
检验,当时,,
是分式方程的解,且符合题意,
.
答:航空模型的单价为125元,航海模型的单价为90元.
(2)设购买航空模型m个,学校花费W元,则购买航海模型个.
根据题意,得,
解得.
根据题意,得,
,
当时,W取最小值,最小值为,
此时.
答:购买航空模型40个,航海模型80个,学校花费最少.
22.答案:(1)
(2)见解析
(3)
解析:(1)反比例函数的图象经过点,
,
,
这个反比例函数的表达式为;
(2)当时,,
当时,,
当时,,
反比例函数的图象经过,,,
画图如下:
(3)向左平移后,E在反比例函数的图象上,
平移后点E对应点的纵坐标为4,
当时,,解得,
平移距离为,
故答案为:.
23.答案:(1)
(2)
解析:(I)设,由,得.
,垂足为C,
.
在中,,,
.
在中,,,
.
.得.
答:线段的长约为.
(II)在中,,,
.
.
答:桥塔的高度约为.
24.答案:(1)
(2),
(3)
解析:(1)抛物线与x轴交于,两点,
解得
该抛物线的表达式为.
(2)对于,令,则,
,
设直线BC的表达式为.
将,分别代入,
得解得
直线BC的表达式为.
过点D作y轴的平行线交BC于点E,点D的横坐标为t,
,,
点D在直线BC下方的抛物线上,
,,
(3),
求的最大值,即为求的最大值.
如图,过点A作轴,交BC于点G.
则,,
,
把代入,得,
,
当时,的值最大,为.
的最大值为.
25.答案:(1)1
(2)
(3)证明见解析
解析:(1)如图1,设与交于点G,
∵四边形是正方形,
∴,,
∵,
∴,
∴,,
∴,
在和中,
,
∴,
∴,
∴;
(2)如图2,设与交于点G,
∵四边形是矩形,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴;
(3)证明:如图3,过点C作交AF的延长线于点H,
∵,
∴,
∴四边形为矩形,
∴,,
∴,,
∴,
∴,
∴,
∴.
【满分150分 考试时间120分钟】
一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.[2024年辽宁中考真题]亚洲、欧洲、非洲和南美洲的最低海拔如下表:
大洲 亚洲 欧洲 非洲 南美洲
最低海拔/m
其中最低海拔最小的大洲是( )
A.亚洲 B.欧洲 C.非洲 D.南美洲
2.[2024年黑龙江哈尔滨中考真题]剪纸是我国最古老的民间艺术之一.下列剪纸图案中既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3.[2024年湖南中考真题]下列计算正确的是( )
A. B. C. D.
4.[2024年河南中考真题]信阳毛尖是中国十大名茶之一.如图是信阳毛尖茶叶的包装盒,它的主视图为( )
A. B. C. D.
5.[2024年西藏中考真题]如图,已知直线,于点D,,则的度数是( )
A. B. C. D.
6.[2024年重庆中考真题]已知,则实数m的范围是( )
A. B. C. D.
7.[2024年江苏宿迁中考真题]规定:对于任意实数a、b、c,有,其中等式右面是通常的乘法和加法运算,如.若关于x的方程有两个不相等的实数根,则m的取值范围为( )
A. B. C.且 D.且
8.[2024年黑龙江牡丹江中考真题]如图是由一些同样大小的三角形按照一定规律所组成的图形,第1个图有4个三角形.第2个图有7个三角形,第3个图有10个三角形……按照此规律排列下去,第674个图中三角形的个数是( )
A.2022 B.2023 C.2024 D.2025
9.[2024年河南中考真题]如图,是边长为的等边三角形的外接圆,点D是的中点,连接,.以点D为圆心,的长为半径在内画弧,则阴影部分的面积为( )
A. B. C. D.
10.[2024年浙江中考真题]如图,在中,,相交于点O,,.过点A作的垂线交于点E,记长为x,长为y.当x,y的值发生变化时,下列代数式的值不变的是( )
A. B. C. D.
二、填空题(本大题共6小题,每小题4分,共24分.请把答案填在题中横线上)
11.[2024年甘肃甘南州中考真题]若分式的值为0,则x的值为______.
12.[2024年江苏苏州中考真题]如图,正八边形转盘被分成八个面积相等的三角形,任意转动这个转盘一次,当转盘停止转动时,指针落在阴影部分的概率是______.
13.[2024年山东烟台中考真题]若一元二次方程的两根为m,n,则的值为___________.
14.[2024年四川巴中中考真题]如图,四边形ABCD是的内接四边形,若四边形OABC为菱形,则的度数是__________.
15.[2024年重庆中考真题]若关于x的不等式组至少有2个整数解,且关于y的分式方程的解为非负整数,则所有满足条件的整数a的值之和为______.
16.[2024年四川宜宾中考真题]如图,正方形的边长为1,M、N是边、上的动点.若,则的最小值为__________.
三、解答题(本大题共9小题,共86分.解答应写出必要的文字说明,证明过程或演算步骤)
17.(8分)[2024年内蒙古中考真题]计算:.
18.(8分)[2024年江苏宿迁中考真题]先化简再求值:,其中.
19.(10分)[2024年广西中考真题]如图,在中,,.
(1)尺规作图:作线段的垂直平分线l,分别交,于点D,E:(要求:保留作图痕迹,不写作法,标明字母)
(2)在(1)所作的图中,连接,若,求的长.
20.(10分)[2024年陕西中考真题]水资源问题是全球关注的热点,节约用水已成为全民共识.某校课外兴趣小组想了解居民家庭用水情况,他们从一小区随机抽取了30户家庭,收集了这30户家庭去年7月份的用水量,并对这30个数据进行整理,绘制了如下统计图表:
组别 用水量 组内平均数
A
B
C
D
根据以上信息,解答下列问:
(1)这30个数据的中位数落在________组(填组别);
(2)求这30户家庭去年7月份的总用水量;
(3)该小区有1000户家庭,若每户家庭今年7月份的用水量都比去年7月份各自家庭的用水量节约,请估计这1000户家庭今年7月份的总用水量比去年7月份的总用水量节约多少
21.(10分)为培养学生的创新意识,提高学生的动手能力,某校计划购买一批航空、航海模型,已知商场某品牌航空模型的单价比航海模型的单价多35元,用2000元购买航空模型的数量是用1800元购买航海模型数量的.
(1)求航空和航海模型的单价;
(2)学校采购时恰逢该商场“六一儿童节”促销:航空模型八折优惠.若购买航空、航海模型共120个,且航空模型数量不少于航海模型数量的,请问分别购买多少个航空和航海模型,学校花费最少?
22.(10分)[2024年河南中考真题]如图,矩形的四个顶点都在格点(网格线的交点)上,对角线,相交于点E,反比例函数的图象经过点A.
(1)求这个反比例函数的表达式.
(2)请先描出这个反比例函数图象上不同于点A的三个格点,再画出反比例函数的图象.
(3)将矩形向左平移,当点E落在这个反比例函数的图象上时,平移的距离为________.
23.(10分)[2024年天津中考真题]综合与实践活动中,要用测角仪测量天津海河上一座桥的桥塔的高度(如图①).某学习小组设计了一个方案:如图②,点C,D,E依次在同一条水平直线上,,,垂足为C.在D处测得桥塔顶部B的仰角()为,测得桥塔底部A的俯角()为,又在E处测得桥塔顶部B的仰角()为.
(1)求线段的长(结果取整数);
(2)求桥塔的高度(结果取整数).
参考数据:,.
24.(10分)[2024年山东东营中考真题]如图,在平面直角坐标系中,已知抛物线与x轴交于,两点,与y轴交于点C,点D是抛物线上的一个动点.
(1)求抛物线的表达式;
(2)当点D在直线BC下方的抛物线上时,过点D作y轴的平行线交BC于点E,设点D的横坐标为t,DE的长为l,请写出l关于t的函数表达式,并写出自变量t的取值范围;
(3)在(2)的条件下,连接AD,交BC于点F,求的最大值.
25.(10分)[2024年甘肃甘南州中考真题]某学校数学兴趣小组在数学课外活动中,对多边形内两条互相垂直的线段做了如下探究:
(1)如图1,在正方形中,点E,F分别是,上的两点,连接,,且,猜想并计算的值;
(2)如图2,在矩形中,,点E是上的一点,连接,,且,求的值;
(3)如图3,在四边形中,,点E为上一点,连接,过点C作的垂线交的延长线于点G,交的延长线于点F,求证:.
参考答案
1.答案:A
解析:,,,,
,
,
海拔最低的是亚洲.
故选:A.
2.答案:D
解析:A.图形既不是轴对称图形,也不是中心对称图形,故此选项不符合题意;
B.图形是中心对称图形,但不是轴对称图形,故此选项不合题意;
C.图形是轴对称图形,但不是中心对称图形,故此选项不合题意;
D.图形既是轴对称图形又是中心对称图形,故此选项符合题意.
故选:D.
3.答案:B
解析:A、,故该选项不正确,不符合题意;
B、,故该选项正确,符合题意;
C、,故该选项不正确,不符合题意;
D、,故该选项不正确,不符合题意;
故选:B.
4.答案:A
解析:这个茶叶盒的主视图为:
故选:A.
5.答案:A
解析:∵,,
∴,
∵,
∴,
∴,故A正确.
故选:A.
6.答案:B
解析:,
,
,
故选:B.
7.答案:D
解析:,
,即,
关于x的方程有两个不相等的实数根,
,且,
解得且,
故选:D.
8.答案:B
解析:第1个图案有4个三角形,即,
第2个图案有7个三角形,即,
第3个图案有10个三角形,即,
…,
按此规律摆下去,第n个图案有个三角形,
则第674个图案中三角形的个数为:(个).
故选:B.
9.答案:C
解析:如图,连接、、,交于点H,
为等边三角形,
,
,,
是弧的中点,
,,,
,
,,
为等边三角形,
,
,
故选:C.
10.答案:C
解析:过点D作交的延长线于点F,
的垂线交于点E,
,
四边形是平行四边形,
,,
,
,,
由勾股定理可得,,
,
,
即,解得,
当x,y的值发生变化时,代数式的值不变的是,
故选:C.
11.答案:-2
解析:分式的值为0,
解得:,
故答案为:-2.
12.答案:
解析:根据题意可知,正八边形转盘被分成八个面积相等的三角形,
其中阴影部分的面积为3个面积相等的三角形,
指针落在阴影部分的概率等于阴影部分的面积除以正八边形的面积,即,
故答案为:.
13.答案:6
解析:一元二次方程的两根为m,n,
,,,.
14.答案:
解析:四边形OABC为菱形,
,
由圆周角定理得:,
四边形ABCD为的内接四边形,
,
,解得:,
故答案为:.
15.答案:16
解析:,
解①得:,
解②得:,
关于x的一元一次不等式组至少有两个整数解,
,
解得,
解方程,得,
关于y的分式方程的解为非负整数,
且,是偶数,
解得且,a是偶数,
且,a是偶数,
则所有满足条件的整数a的值之和是,
故答案为:16.
16.答案:/
解析:正方形的边长为1,
,,
将顺时针旋转得到,则,
,,,,
点P、B、M、C共线,
,
,
,,,
,
,
,
设,,则,,
,
∵,
,即,
整理得:,
,
当且仅当,即,也即时,取最小值,
故答案为:.
17.答案:11
解析:
.
18.答案:,
解析:
,
当时,原式.
19.答案:(1)见详解
(2)
解析:(1)如下直线l即为所求.
(2)连接如下图:
为线段的垂直平分线,
,
,
,
为等腰直角三角形,
,
.
20.答案:(1)B
(2)
(3)
解析:(1)根据条形统计图可知:组有10户,B组有12户,C组有6户,D组有2户,
将30个数据从小到大进行排序,排在第15和16的两个数据一定落在B组,
这30个数据的中位数落在B组;
(2)这30户家庭去年7月份的总用水量为:
;
(3)去年每户家庭7月份的用水量约为:,
每户家庭今年7月份的用水量都比去年7月份各自家庭的用水量节约,
今年每户家庭7月份的节约用水量约为:,
估计这1000户家庭今年7月份的总用水量比去年7月份的总用水量节约:
.
21.答案:(1)航空模型的单价为125元,航海模型的单价为90元
(2)购买航空模型40个,航海模型80个,学校花费最少
解析:(1)设航空模型的单价为x元,则航海模型的单价为元,
根据题意,得,
解得,
检验,当时,,
是分式方程的解,且符合题意,
.
答:航空模型的单价为125元,航海模型的单价为90元.
(2)设购买航空模型m个,学校花费W元,则购买航海模型个.
根据题意,得,
解得.
根据题意,得,
,
当时,W取最小值,最小值为,
此时.
答:购买航空模型40个,航海模型80个,学校花费最少.
22.答案:(1)
(2)见解析
(3)
解析:(1)反比例函数的图象经过点,
,
,
这个反比例函数的表达式为;
(2)当时,,
当时,,
当时,,
反比例函数的图象经过,,,
画图如下:
(3)向左平移后,E在反比例函数的图象上,
平移后点E对应点的纵坐标为4,
当时,,解得,
平移距离为,
故答案为:.
23.答案:(1)
(2)
解析:(I)设,由,得.
,垂足为C,
.
在中,,,
.
在中,,,
.
.得.
答:线段的长约为.
(II)在中,,,
.
.
答:桥塔的高度约为.
24.答案:(1)
(2),
(3)
解析:(1)抛物线与x轴交于,两点,
解得
该抛物线的表达式为.
(2)对于,令,则,
,
设直线BC的表达式为.
将,分别代入,
得解得
直线BC的表达式为.
过点D作y轴的平行线交BC于点E,点D的横坐标为t,
,,
点D在直线BC下方的抛物线上,
,,
(3),
求的最大值,即为求的最大值.
如图,过点A作轴,交BC于点G.
则,,
,
把代入,得,
,
当时,的值最大,为.
的最大值为.
25.答案:(1)1
(2)
(3)证明见解析
解析:(1)如图1,设与交于点G,
∵四边形是正方形,
∴,,
∵,
∴,
∴,,
∴,
在和中,
,
∴,
∴,
∴;
(2)如图2,设与交于点G,
∵四边形是矩形,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴;
(3)证明:如图3,过点C作交AF的延长线于点H,
∵,
∴,
∴四边形为矩形,
∴,,
∴,,
∴,
∴,
∴,
∴.
同课章节目录
