2025届中考数学全真模拟卷 【山西专用】(含详解)
文档属性
| 名称 | 2025届中考数学全真模拟卷 【山西专用】(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-07 19:33:21 | ||
图片预览



文档简介
2025届中考数学全真模拟卷 【山西专用】
【满分120分】
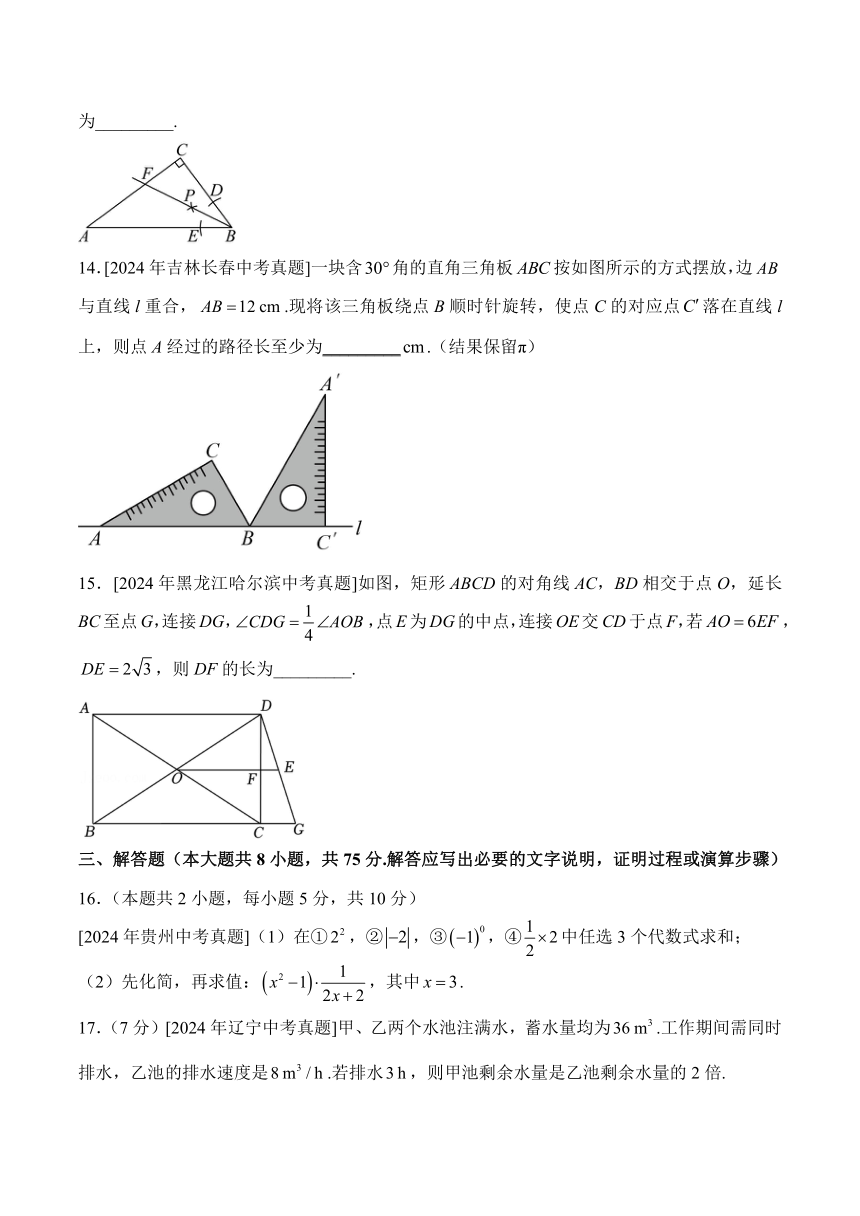
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
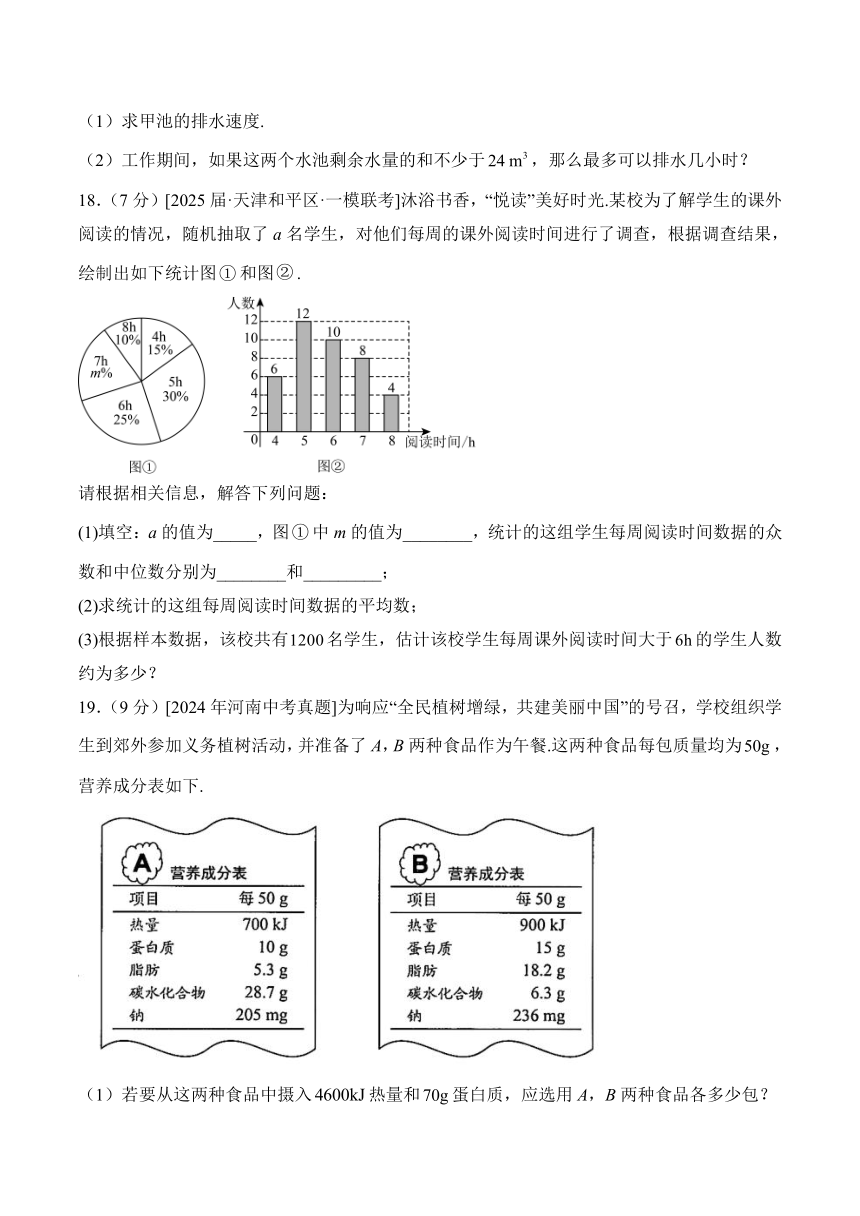
1.[2024年湖南长沙中考真题]“玉兔号”是我国首辆月球车,它和着陆器共同组成“嫦娥三号”探测器.“玉兔号”月球车能够耐受月球表面的最低温度是、最高温度是,则它能够耐受的温差是( )
A. B. C. D.
2.[2025届·江西抚州·二模]下图是江西省部分大学的校徽,忽略各个图案中的文字,其中图案部分是轴对称图形的是( )
A. B. C. D.
3.[2024年山东泰安中考真题]下列运算正确的是( )
A. B.
C. D.
4.[2024年福建中考真题]据《人民日报》3月12日电,世界知识产权组织近日公布数据显示,2023年,全球PCT(《专利合作条约》)国际专利申请总量为27.26万件,中国申请量为69610件,是申请量最大的来源国.数据69610用科学记数法表示为( )
A. B. C. D.
5.[2024年西藏中考真题]如图,为的直径,点B,D在上,,,则的长为( )
A.2 B. C. D.4
6.[2024年黑龙江哈尔滨中考真题]一个有进水管与出水管的容器,从某时刻开始5min内只进水不出水,在随后的10min内既进水又出水,每分的进水量和出水量是两个常数.容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示,当时,( )
A.36L B.38L C.40L D.42L
7.[2025届·山西太原·二模]如图,同学们将平行于凸透镜主光轴的红光和紫光射入同一个凸透镜,折射光线交于点O,与主光轴分别交于点,,由此发现凸透镜的焦点略有偏差.若,,则的度数为( )
A. B. C. D.
8.[2024年天津中考真题]若点,,都在反比例函数的图象上,则,,的大小关系是( )
A. B. C. D.
9.[2024年河南中考真题]豫剧是国家级非物质文化遗产,因其雅俗共赏,深受大众喜爱.正面印有豫剧经典剧目人物的三张卡片如图所示,它们除正面外完全相同.把这三张卡片背面朝上洗匀,从中随机抽取一张,放回洗匀后,再从中随机抽取一张,两次抽取的卡片正面相同的概率为( )
A. B. C. D.
10.[2024年浙江中考真题]如图,在中,,相交于点O,,.过点A作的垂线交于点E,记长为x,长为y.当x,y的值发生变化时,下列代数式的值不变的是( )
A. B. C. D.
二、填空题(本大题共5小题,每小题3分,共15分.请把答案填在题中横线上)
11.[2024年江苏淮安中考真题]计算:______.
12.[2024年山东泰安中考真题]如图所示,是用图形“○”和“●”按一定规律摆成的“小屋子”.
按照此规律继续摆下去,第___________个“小屋子”中图形“○”的个数是图形“●”个数的3倍.
13.[2024年西藏中考真题]如图,在中,,以点B为圆心,适当长为半径作弧,分别交,于点D,E,再分别以点D,E为圆心,大于的长为半径作弧,两弧在的内部相交于点P,作射线交于点F.已知,,则的长为_________.
14.[2024年吉林长春中考真题]一块含角的直角三角板按如图所示的方式摆放,边与直线l重合,.现将该三角板绕点B顺时针旋转,使点C的对应点落在直线l上,则点A经过的路径长至少为_________.(结果保留π)
15.[2024年黑龙江哈尔滨中考真题]如图,矩形ABCD的对角线AC,BD相交于点O,延长BC至点G,连接DG,,点E为DG的中点,连接OE交CD于点F,若,,则DF的长为_________.
三、解答题(本大题共8小题,共75分.解答应写出必要的文字说明,证明过程或演算步骤)
16.(本题共2小题,每小题5分,共10分)
[2024年贵州中考真题](1)在①,②,③,④中任选3个代数式求和;
(2)先化简,再求值:,其中.
17.(7分)[2024年辽宁中考真题]甲、乙两个水池注满水,蓄水量均为.工作期间需同时排水,乙池的排水速度是.若排水,则甲池剩余水量是乙池剩余水量的2倍.
(1)求甲池的排水速度.
(2)工作期间,如果这两个水池剩余水量的和不少于,那么最多可以排水几小时?
18.(7分)[2025届·天津和平区·一模联考]沐浴书香,“悦读”美好时光.某校为了解学生的课外阅读的情况,随机抽取了a名学生,对他们每周的课外阅读时间进行了调查,根据调查结果,绘制出如下统计图和图.
请根据相关信息,解答下列问题:
(1)填空:a的值为_____,图中m的值为________,统计的这组学生每周阅读时间数据的众数和中位数分别为________和_________;
(2)求统计的这组每周阅读时间数据的平均数;
(3)根据样本数据,该校共有名学生,估计该校学生每周课外阅读时间大于的学生人数约为多少?
19.(9分)[2024年河南中考真题]为响应“全民植树增绿,共建美丽中国”的号召,学校组织学生到郊外参加义务植树活动,并准备了A,B两种食品作为午餐.这两种食品每包质量均为,营养成分表如下.
(1)若要从这两种食品中摄入热量和蛋白质,应选用A,B两种食品各多少包?
(2)运动量大的人或青少年对蛋白质的摄入量应更多.若每份午餐选用这两种食品共7包,要使每份午餐中的蛋白质含量不低于,且热量最低,应如何选用这两种食品?
20.(9分)[2024年西藏中考真题]在数学综合实践活动中,次仁和格桑自主设计了“测量家附近的一座小山高度”的探究作业.如图,次仁在A处测得山顶C的仰角为;格桑在B处测得山顶C的仰角为.已知两人所处位置的水平距离米,A处距地面的垂直高度米,B处距地面的垂直高度米,点M,F,N在同一条直线上,求小山的高度.(结果保留根号)
21.(8分)[2025届·山西运城·二模]下面是先锋小组研究性学习报告的部分内容,请认真阅读,并完成相应任务.
关于“相似扇形”的研究报告 先锋小组 研究对象:相似扇形 研究思路:类比研究相似三角形,按“概念—性质—判定—应用”的路径,由一般到特殊进行研究. 研究内容: 【概念理解】圆心角相等的两个扇形叫做相似扇形,其半径的比叫做相似比,如图1,分别以线段 为直径作半圆O与半圆,即可得到一对相似扇形,其相似比为. 【性质探索】可以类比相似三角形的性质,得到相似扇形的性质,如下: 关于弧长:两个相似扇形的相似比为k,则弧长之比为①_______; 关于面积:两个相似扇形的相似比为k,则面积之比为②_____. …… 【判定探索】根据定义,探索相似扇形的判定,得到如下结论: 半径和弧长对应成比例的两个扇形是相似扇形.为说明这一结论正确,分析如下: 如图2,已知扇形与扇形,,只要说明, 即可判断扇形与扇形是相似扇形. ……
任务:
(1)补全材料中“性质探索”中空缺的部分:①_____;②_____;
(2)根据材料中“判定探索”的分析思路,写出推理过程;
(3)如图3,已知扇形,点P是上的一点,扇形与扇形相似,且点P在的垂直平分线上,若的长为l,则的长为_______.(用含l的代数式表示)
22.(12分)[2024年山东济宁中考真题]综合与实践
某校数学课外活动小组用一张矩形纸片(如图(1),矩形ABCD中,且AB足够长)进行探究活动.
【动手操作】
如图(2),第一步,沿点A所在直线折叠,使点D落在AB上的点E处,折痕为AF,连接EF,把纸片展平.第二步,把四边形AEFD折叠,使点A与点E重合,点D与点F重合,折痕为GH,再把纸片展平.
第三步,连接GF.
【探究发现】
根据以上操作,甲、乙两同学分别写出了一个结论.
甲同学的结论:四边形AEFD是正方形.
乙同学的结论:.
(1)请分别判断甲、乙两同学的结论是否正确.若正确,写出证明过程;若不正确,请说明理由.
【继续探究】
在上面操作的基础上,丙同学继续操作.
如图(3),第四步,沿点G所在直线折叠,使点F落在AB上的点M处,折痕为GP,连接PM,把纸片展平.
第五步,连接FM交GP于点N.
根据以上操作,丁同学写出了一个正确结论:.
(2)请证明这个结论.
23.(13分)[2024年辽宁中考真题]已知是自变量x的函数,当时,称函数为函数的“升幂函数”.在平面直角坐标系中,对于函数图象上任意一点,称点为点A“关于的升幂点”,点B在函数的“升幂函数”的图象上.例如:函数,当时,则函数是函数的“升幂函数”.在平面直角坐标系中,函数的图象上任意一点,点为点A“关于的升幂点”,点B在函数的“升幂函数”的图象上.
(1)求函数的“升幂函数”的函数表达式;
(2)如图1,点A在函数的图象上,点A“关于的升幂点”B在点A上方,当时,求点A的坐标;
(3)点A在函数的图象上,点A “关于的升幂点”为点B,设点A的横坐标为m.
①若点B与点A重合,求m的值;
②若点B在点A的上方,过点B作x轴的平行线,与函数的“升幂函数”的图象相交于点C,以,为邻边构造矩形,设矩形的周长为y,求y关于m的函数表达式;
③在②的条件下,当直线与函数y的图象的交点有3个时,从左到右依次记为E,F,G,当直线与函数y的图象的交点有2个时,从左到右依次记为M,N,若,请直接写出的值.
参考答案
1.答案:D
解析:由题意,得,故选D.
2.答案:B
解析:A、不是轴对称图形,不符合题意;
B、是轴对称图形,符合题意;
C、不是轴对称图形,不符合题意;
D、不是轴对称图形,不符合题意;
故选:B.
3.答案:D
解析:A、与不是同类项,不能合并同类项,故不符合题意;
B、,故不符合题意;
C、,故不符合题意;
D、,故符合题意;
故选:D.
4.答案:C
解析:.
故选:C.
5.答案:C
解析:∵为的直径,
∴,
∵,,
∴,
∴,
∵,
∴,
∴,
故选:C.
6.答案:B
解析:设当时的直线方程为:.
图象过、,
.
.
.
令,
.
故选:B.
7.答案:D
解析:如图,
由题意知,
,,
,,
,,
,
,
故选D.
8.答案:B
解析:,
反比例函数的图象分布在第一、三象限,在每个象限内,y随x的增大而减小,
点,,都在反比例函数的图象上,
点分布在第三象限,,分布在第一象限,且,
,,
,
故选:B.
9.答案:D
解析:将三张卡片分别记为A,B,C,
列表如下:
A B C
A
B
C
共有9种等可能的结果,其中两次抽取的卡片,正面相同的结果有3种,
两次抽取的卡片正面相同的概率为.
故选:D.
10.答案:C
解析:过点D作交的延长线于点F,
的垂线交于点E,
,
四边形是平行四边形,
,,
,
,,
由勾股定理可得,,
,
,
即,解得,
当x,y的值发生变化时,代数式的值不变的是,
故选:C.
11.答案:2
解析:原式.
12.答案:12
解析:分析如下:
“小屋子”编号 “小屋子”中“○”个数 “小屋子”中“●”个数
第1个
第2个
第3个
第4个
… … …
第n个
令,解得,.为正整数,.故第12个“小屋子”中图形“○”的个数是图形“●”个数的3倍.
13.答案:
解析:过F作于G,
由作图得:平分,,,
∴,
在中根据勾股定理得:,
,,
,
,
设,则,,
在中,根据勾股定理得:
,
即:,
解得:,
,
在中根据勾股定理得:.
故答案为:.
14.答案:
解析:将该三角板绕点B顺时针旋转,使点C的对应点落在直线l上,
,即,
点A经过的路径长至少为.
故答案为:.
15.答案:
解析:连接,设,
在矩形中,,
则,
,
是中点,
,
,,,
,
,
,
,
,
,
,
,
,
,,
,
,
.
16.答案:(1)见解析
(2),1
解析:(1)选择①,②,③,
;
选择①,②,④,
;
选择①,③,④,
;
选择②,③,④,
;
(2)
;
当时,原式.
17.答案:(1)
(2)
解析:(1)设甲池的排水速度为,
根据题意得,,解得.
答:甲池的排水速度为.
(2)设排水,则,解得.
答:最多可以排水.
18.答案:(1)40,20,5,6;
(2)这组每周阅读时间数据的平均数为5.8;
(3)估计该校学生每周课外阅读时间大于的学生人数约为360人.
解析:由条形统计图可知(人),
∵,
∴,
由条形统计图可知每周阅读时间的人数最多,故众数为5,
∵随机抽取了40名学生,
∴中位数为第20,21名学生的平均数,由条形统计图可知第20,21名学生的平均数为6,
故答案为:40,20,6,6;
(2)解析:观察条形统计图可知,
这组每周阅读时间数据的平均数为
,
答:这组每周阅读时间数据的平均数为5.8;
(3)解析:该校学生每周课外阅读时间大于的学生人数(人),
答:估计该校学生每周课外阅读时间大于的学生人数约为人.
19.答案:(1)选用A种食品4包,B种食品2包
(2)选用A种食品3包,B种食品4包
解析:(1)设选用A种食品x包,B种食品y包
根据题意,得
解得.
答:选用A种食品4包,B种食品2包.
(2)设选用A种食品m包,则选用B种食品包,
根据题意,得.
解得.
设每份午餐的总热量为,则
,随m的增大而减小.
当时,w取得最小值,此时.
答:选用A种食品3包,B种食品4包.
20.答案:米
解析:根据题意可得:,,
∴四边形和四边形为矩形,
∴米,米,,,
∴(米),
设,则米,
∵,,
∴,
∵,,
∴,
∴,,
∵米,
∴,
解得:,
∴米.
21.答案:(1)k,;
(2)证明见解析
(3)
解析:类比相似三角形的性质,得到相似扇形的性质,如下:
关于弧长:两个相似扇形的相似比为k,则弧长之比为k;
关于面积:两个相似扇形的相似比为k,则面积之比为.
(2)解析:∵,
∴,
解得:,
∴扇形与扇形是相似扇形.
(3)解析:∵扇形与扇形相似,
∴,
∵,,
∴,
∵点P在的垂直平分线上,
∴,
∴,
∵,,
∴,
∴,
设,,
∴,
整理得:,
解得:,(舍去),
∴,
∵的长为l,
∴,
∴;
22.答案:(1)甲、乙同学的结论都正确,证明见解析
(2)证明见解析
解析:(1)甲、乙同学的结论都正确.
证明:四边形ABCD是矩形,
.
又由折叠知,
四边形AEFD为矩形.
又,
四边形AEFD为正方形.
故甲同学的结论正确.
如图(1),过点G作于点K.
由折叠知.
设,
则,,
,
,
,
故乙同学的结论正确.
(2)证明:如图(2),过点G作于点O.
由折叠可知,,,,,
四边形ABCD是矩形,,
,
,
,
,
四边形FGMP是菱形,
,,
,
,
.
,
.
,
.
23.答案:(1)
(2)
(3)①或;②;③或
解析:(1)根据题意得:,
故答案为:,
(2)设点,则,
,B在点A上方,
,解得:,
;
(3)①根据题意得:,则,
点B与点A重合,
,解得:或,
②根据题意得:,
对称轴为,B、C关于对称轴对称,
,则,
,解得:,
,,
点B在点A的上方,
,解得:,
,
当,点B在点C右侧时,,,
当,点B在点C左侧时,,,
,
③∵,
,,
当时,,
当时,,
当时,,
,,,
当时,直线与函数y的图象有3个交点,
当时,直线与函数y的图象有2个交点,
直线与函数y交于E、F两点,,即:,
,,,
直线与函数y交于M、N两点,,即:,
,,,
,
,整理得:,
当时,
,解得:或(舍),
,
,解得:,
,
或.
【满分120分】
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.[2024年湖南长沙中考真题]“玉兔号”是我国首辆月球车,它和着陆器共同组成“嫦娥三号”探测器.“玉兔号”月球车能够耐受月球表面的最低温度是、最高温度是,则它能够耐受的温差是( )
A. B. C. D.
2.[2025届·江西抚州·二模]下图是江西省部分大学的校徽,忽略各个图案中的文字,其中图案部分是轴对称图形的是( )
A. B. C. D.
3.[2024年山东泰安中考真题]下列运算正确的是( )
A. B.
C. D.
4.[2024年福建中考真题]据《人民日报》3月12日电,世界知识产权组织近日公布数据显示,2023年,全球PCT(《专利合作条约》)国际专利申请总量为27.26万件,中国申请量为69610件,是申请量最大的来源国.数据69610用科学记数法表示为( )
A. B. C. D.
5.[2024年西藏中考真题]如图,为的直径,点B,D在上,,,则的长为( )
A.2 B. C. D.4
6.[2024年黑龙江哈尔滨中考真题]一个有进水管与出水管的容器,从某时刻开始5min内只进水不出水,在随后的10min内既进水又出水,每分的进水量和出水量是两个常数.容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示,当时,( )
A.36L B.38L C.40L D.42L
7.[2025届·山西太原·二模]如图,同学们将平行于凸透镜主光轴的红光和紫光射入同一个凸透镜,折射光线交于点O,与主光轴分别交于点,,由此发现凸透镜的焦点略有偏差.若,,则的度数为( )
A. B. C. D.
8.[2024年天津中考真题]若点,,都在反比例函数的图象上,则,,的大小关系是( )
A. B. C. D.
9.[2024年河南中考真题]豫剧是国家级非物质文化遗产,因其雅俗共赏,深受大众喜爱.正面印有豫剧经典剧目人物的三张卡片如图所示,它们除正面外完全相同.把这三张卡片背面朝上洗匀,从中随机抽取一张,放回洗匀后,再从中随机抽取一张,两次抽取的卡片正面相同的概率为( )
A. B. C. D.
10.[2024年浙江中考真题]如图,在中,,相交于点O,,.过点A作的垂线交于点E,记长为x,长为y.当x,y的值发生变化时,下列代数式的值不变的是( )
A. B. C. D.
二、填空题(本大题共5小题,每小题3分,共15分.请把答案填在题中横线上)
11.[2024年江苏淮安中考真题]计算:______.
12.[2024年山东泰安中考真题]如图所示,是用图形“○”和“●”按一定规律摆成的“小屋子”.
按照此规律继续摆下去,第___________个“小屋子”中图形“○”的个数是图形“●”个数的3倍.
13.[2024年西藏中考真题]如图,在中,,以点B为圆心,适当长为半径作弧,分别交,于点D,E,再分别以点D,E为圆心,大于的长为半径作弧,两弧在的内部相交于点P,作射线交于点F.已知,,则的长为_________.
14.[2024年吉林长春中考真题]一块含角的直角三角板按如图所示的方式摆放,边与直线l重合,.现将该三角板绕点B顺时针旋转,使点C的对应点落在直线l上,则点A经过的路径长至少为_________.(结果保留π)
15.[2024年黑龙江哈尔滨中考真题]如图,矩形ABCD的对角线AC,BD相交于点O,延长BC至点G,连接DG,,点E为DG的中点,连接OE交CD于点F,若,,则DF的长为_________.
三、解答题(本大题共8小题,共75分.解答应写出必要的文字说明,证明过程或演算步骤)
16.(本题共2小题,每小题5分,共10分)
[2024年贵州中考真题](1)在①,②,③,④中任选3个代数式求和;
(2)先化简,再求值:,其中.
17.(7分)[2024年辽宁中考真题]甲、乙两个水池注满水,蓄水量均为.工作期间需同时排水,乙池的排水速度是.若排水,则甲池剩余水量是乙池剩余水量的2倍.
(1)求甲池的排水速度.
(2)工作期间,如果这两个水池剩余水量的和不少于,那么最多可以排水几小时?
18.(7分)[2025届·天津和平区·一模联考]沐浴书香,“悦读”美好时光.某校为了解学生的课外阅读的情况,随机抽取了a名学生,对他们每周的课外阅读时间进行了调查,根据调查结果,绘制出如下统计图和图.
请根据相关信息,解答下列问题:
(1)填空:a的值为_____,图中m的值为________,统计的这组学生每周阅读时间数据的众数和中位数分别为________和_________;
(2)求统计的这组每周阅读时间数据的平均数;
(3)根据样本数据,该校共有名学生,估计该校学生每周课外阅读时间大于的学生人数约为多少?
19.(9分)[2024年河南中考真题]为响应“全民植树增绿,共建美丽中国”的号召,学校组织学生到郊外参加义务植树活动,并准备了A,B两种食品作为午餐.这两种食品每包质量均为,营养成分表如下.
(1)若要从这两种食品中摄入热量和蛋白质,应选用A,B两种食品各多少包?
(2)运动量大的人或青少年对蛋白质的摄入量应更多.若每份午餐选用这两种食品共7包,要使每份午餐中的蛋白质含量不低于,且热量最低,应如何选用这两种食品?
20.(9分)[2024年西藏中考真题]在数学综合实践活动中,次仁和格桑自主设计了“测量家附近的一座小山高度”的探究作业.如图,次仁在A处测得山顶C的仰角为;格桑在B处测得山顶C的仰角为.已知两人所处位置的水平距离米,A处距地面的垂直高度米,B处距地面的垂直高度米,点M,F,N在同一条直线上,求小山的高度.(结果保留根号)
21.(8分)[2025届·山西运城·二模]下面是先锋小组研究性学习报告的部分内容,请认真阅读,并完成相应任务.
关于“相似扇形”的研究报告 先锋小组 研究对象:相似扇形 研究思路:类比研究相似三角形,按“概念—性质—判定—应用”的路径,由一般到特殊进行研究. 研究内容: 【概念理解】圆心角相等的两个扇形叫做相似扇形,其半径的比叫做相似比,如图1,分别以线段 为直径作半圆O与半圆,即可得到一对相似扇形,其相似比为. 【性质探索】可以类比相似三角形的性质,得到相似扇形的性质,如下: 关于弧长:两个相似扇形的相似比为k,则弧长之比为①_______; 关于面积:两个相似扇形的相似比为k,则面积之比为②_____. …… 【判定探索】根据定义,探索相似扇形的判定,得到如下结论: 半径和弧长对应成比例的两个扇形是相似扇形.为说明这一结论正确,分析如下: 如图2,已知扇形与扇形,,只要说明, 即可判断扇形与扇形是相似扇形. ……
任务:
(1)补全材料中“性质探索”中空缺的部分:①_____;②_____;
(2)根据材料中“判定探索”的分析思路,写出推理过程;
(3)如图3,已知扇形,点P是上的一点,扇形与扇形相似,且点P在的垂直平分线上,若的长为l,则的长为_______.(用含l的代数式表示)
22.(12分)[2024年山东济宁中考真题]综合与实践
某校数学课外活动小组用一张矩形纸片(如图(1),矩形ABCD中,且AB足够长)进行探究活动.
【动手操作】
如图(2),第一步,沿点A所在直线折叠,使点D落在AB上的点E处,折痕为AF,连接EF,把纸片展平.第二步,把四边形AEFD折叠,使点A与点E重合,点D与点F重合,折痕为GH,再把纸片展平.
第三步,连接GF.
【探究发现】
根据以上操作,甲、乙两同学分别写出了一个结论.
甲同学的结论:四边形AEFD是正方形.
乙同学的结论:.
(1)请分别判断甲、乙两同学的结论是否正确.若正确,写出证明过程;若不正确,请说明理由.
【继续探究】
在上面操作的基础上,丙同学继续操作.
如图(3),第四步,沿点G所在直线折叠,使点F落在AB上的点M处,折痕为GP,连接PM,把纸片展平.
第五步,连接FM交GP于点N.
根据以上操作,丁同学写出了一个正确结论:.
(2)请证明这个结论.
23.(13分)[2024年辽宁中考真题]已知是自变量x的函数,当时,称函数为函数的“升幂函数”.在平面直角坐标系中,对于函数图象上任意一点,称点为点A“关于的升幂点”,点B在函数的“升幂函数”的图象上.例如:函数,当时,则函数是函数的“升幂函数”.在平面直角坐标系中,函数的图象上任意一点,点为点A“关于的升幂点”,点B在函数的“升幂函数”的图象上.
(1)求函数的“升幂函数”的函数表达式;
(2)如图1,点A在函数的图象上,点A“关于的升幂点”B在点A上方,当时,求点A的坐标;
(3)点A在函数的图象上,点A “关于的升幂点”为点B,设点A的横坐标为m.
①若点B与点A重合,求m的值;
②若点B在点A的上方,过点B作x轴的平行线,与函数的“升幂函数”的图象相交于点C,以,为邻边构造矩形,设矩形的周长为y,求y关于m的函数表达式;
③在②的条件下,当直线与函数y的图象的交点有3个时,从左到右依次记为E,F,G,当直线与函数y的图象的交点有2个时,从左到右依次记为M,N,若,请直接写出的值.
参考答案
1.答案:D
解析:由题意,得,故选D.
2.答案:B
解析:A、不是轴对称图形,不符合题意;
B、是轴对称图形,符合题意;
C、不是轴对称图形,不符合题意;
D、不是轴对称图形,不符合题意;
故选:B.
3.答案:D
解析:A、与不是同类项,不能合并同类项,故不符合题意;
B、,故不符合题意;
C、,故不符合题意;
D、,故符合题意;
故选:D.
4.答案:C
解析:.
故选:C.
5.答案:C
解析:∵为的直径,
∴,
∵,,
∴,
∴,
∵,
∴,
∴,
故选:C.
6.答案:B
解析:设当时的直线方程为:.
图象过、,
.
.
.
令,
.
故选:B.
7.答案:D
解析:如图,
由题意知,
,,
,,
,,
,
,
故选D.
8.答案:B
解析:,
反比例函数的图象分布在第一、三象限,在每个象限内,y随x的增大而减小,
点,,都在反比例函数的图象上,
点分布在第三象限,,分布在第一象限,且,
,,
,
故选:B.
9.答案:D
解析:将三张卡片分别记为A,B,C,
列表如下:
A B C
A
B
C
共有9种等可能的结果,其中两次抽取的卡片,正面相同的结果有3种,
两次抽取的卡片正面相同的概率为.
故选:D.
10.答案:C
解析:过点D作交的延长线于点F,
的垂线交于点E,
,
四边形是平行四边形,
,,
,
,,
由勾股定理可得,,
,
,
即,解得,
当x,y的值发生变化时,代数式的值不变的是,
故选:C.
11.答案:2
解析:原式.
12.答案:12
解析:分析如下:
“小屋子”编号 “小屋子”中“○”个数 “小屋子”中“●”个数
第1个
第2个
第3个
第4个
… … …
第n个
令,解得,.为正整数,.故第12个“小屋子”中图形“○”的个数是图形“●”个数的3倍.
13.答案:
解析:过F作于G,
由作图得:平分,,,
∴,
在中根据勾股定理得:,
,,
,
,
设,则,,
在中,根据勾股定理得:
,
即:,
解得:,
,
在中根据勾股定理得:.
故答案为:.
14.答案:
解析:将该三角板绕点B顺时针旋转,使点C的对应点落在直线l上,
,即,
点A经过的路径长至少为.
故答案为:.
15.答案:
解析:连接,设,
在矩形中,,
则,
,
是中点,
,
,,,
,
,
,
,
,
,
,
,
,
,,
,
,
.
16.答案:(1)见解析
(2),1
解析:(1)选择①,②,③,
;
选择①,②,④,
;
选择①,③,④,
;
选择②,③,④,
;
(2)
;
当时,原式.
17.答案:(1)
(2)
解析:(1)设甲池的排水速度为,
根据题意得,,解得.
答:甲池的排水速度为.
(2)设排水,则,解得.
答:最多可以排水.
18.答案:(1)40,20,5,6;
(2)这组每周阅读时间数据的平均数为5.8;
(3)估计该校学生每周课外阅读时间大于的学生人数约为360人.
解析:由条形统计图可知(人),
∵,
∴,
由条形统计图可知每周阅读时间的人数最多,故众数为5,
∵随机抽取了40名学生,
∴中位数为第20,21名学生的平均数,由条形统计图可知第20,21名学生的平均数为6,
故答案为:40,20,6,6;
(2)解析:观察条形统计图可知,
这组每周阅读时间数据的平均数为
,
答:这组每周阅读时间数据的平均数为5.8;
(3)解析:该校学生每周课外阅读时间大于的学生人数(人),
答:估计该校学生每周课外阅读时间大于的学生人数约为人.
19.答案:(1)选用A种食品4包,B种食品2包
(2)选用A种食品3包,B种食品4包
解析:(1)设选用A种食品x包,B种食品y包
根据题意,得
解得.
答:选用A种食品4包,B种食品2包.
(2)设选用A种食品m包,则选用B种食品包,
根据题意,得.
解得.
设每份午餐的总热量为,则
,随m的增大而减小.
当时,w取得最小值,此时.
答:选用A种食品3包,B种食品4包.
20.答案:米
解析:根据题意可得:,,
∴四边形和四边形为矩形,
∴米,米,,,
∴(米),
设,则米,
∵,,
∴,
∵,,
∴,
∴,,
∵米,
∴,
解得:,
∴米.
21.答案:(1)k,;
(2)证明见解析
(3)
解析:类比相似三角形的性质,得到相似扇形的性质,如下:
关于弧长:两个相似扇形的相似比为k,则弧长之比为k;
关于面积:两个相似扇形的相似比为k,则面积之比为.
(2)解析:∵,
∴,
解得:,
∴扇形与扇形是相似扇形.
(3)解析:∵扇形与扇形相似,
∴,
∵,,
∴,
∵点P在的垂直平分线上,
∴,
∴,
∵,,
∴,
∴,
设,,
∴,
整理得:,
解得:,(舍去),
∴,
∵的长为l,
∴,
∴;
22.答案:(1)甲、乙同学的结论都正确,证明见解析
(2)证明见解析
解析:(1)甲、乙同学的结论都正确.
证明:四边形ABCD是矩形,
.
又由折叠知,
四边形AEFD为矩形.
又,
四边形AEFD为正方形.
故甲同学的结论正确.
如图(1),过点G作于点K.
由折叠知.
设,
则,,
,
,
,
故乙同学的结论正确.
(2)证明:如图(2),过点G作于点O.
由折叠可知,,,,,
四边形ABCD是矩形,,
,
,
,
,
四边形FGMP是菱形,
,,
,
,
.
,
.
,
.
23.答案:(1)
(2)
(3)①或;②;③或
解析:(1)根据题意得:,
故答案为:,
(2)设点,则,
,B在点A上方,
,解得:,
;
(3)①根据题意得:,则,
点B与点A重合,
,解得:或,
②根据题意得:,
对称轴为,B、C关于对称轴对称,
,则,
,解得:,
,,
点B在点A的上方,
,解得:,
,
当,点B在点C右侧时,,,
当,点B在点C左侧时,,,
,
③∵,
,,
当时,,
当时,,
当时,,
,,,
当时,直线与函数y的图象有3个交点,
当时,直线与函数y的图象有2个交点,
直线与函数y交于E、F两点,,即:,
,,,
直线与函数y交于M、N两点,,即:,
,,,
,
,整理得:,
当时,
,解得:或(舍),
,
,解得:,
,
或.
同课章节目录
