2025届中考数学全真模拟卷 【黑龙江哈尔滨专用】(含详解)
文档属性
| 名称 | 2025届中考数学全真模拟卷 【黑龙江哈尔滨专用】(含详解) | 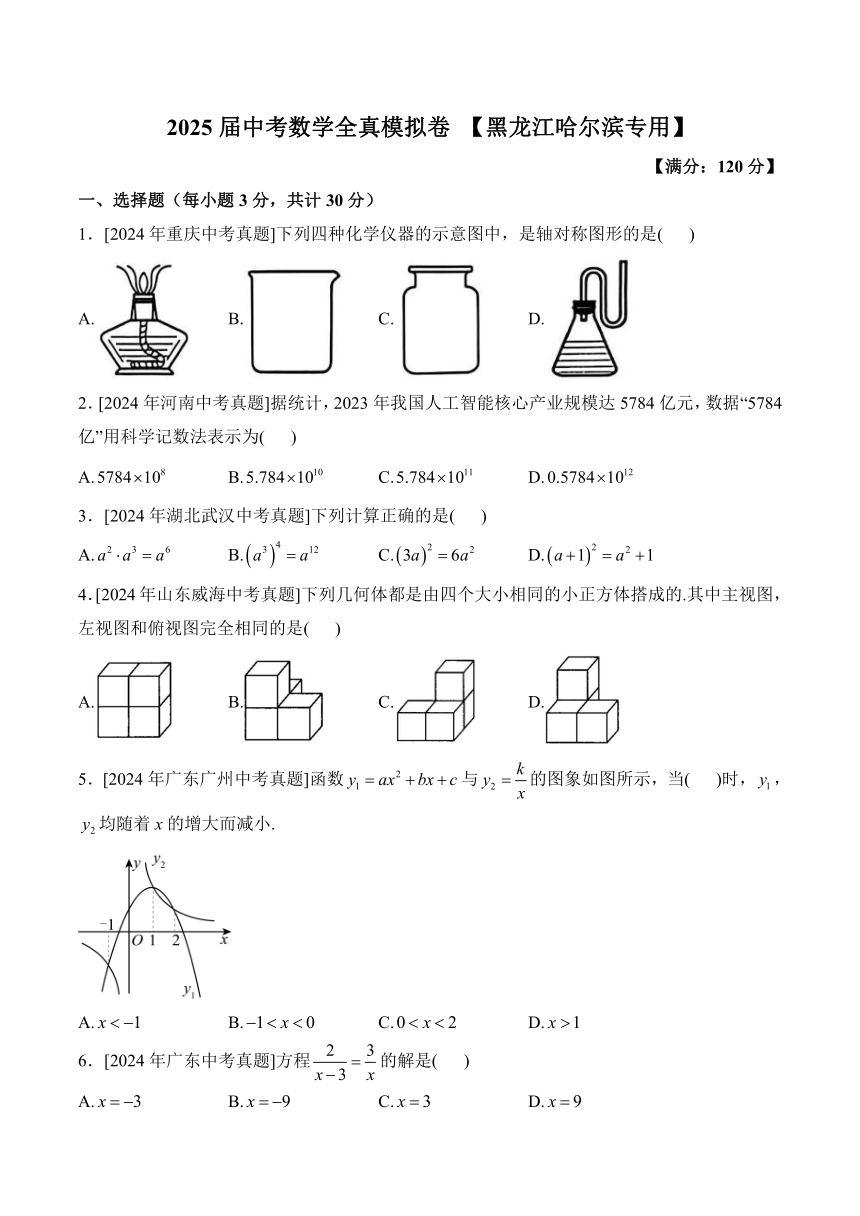 | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-07 19:37:43 | ||
图片预览





文档简介
2025届中考数学全真模拟卷 【黑龙江哈尔滨专用】
【满分:120分】
一、选择题(每小题3分,共计30分)
1.[2024年重庆中考真题]下列四种化学仪器的示意图中,是轴对称图形的是( )
A. B. C. D.
2.[2024年河南中考真题]据统计,2023年我国人工智能核心产业规模达5784亿元,数据“5784亿”用科学记数法表示为( )
A. B. C. D.
3.[2024年湖北武汉中考真题]下列计算正确的是( )
A. B. C. D.
4.[2024年山东威海中考真题]下列几何体都是由四个大小相同的小正方体搭成的.其中主视图,左视图和俯视图完全相同的是( )
A. B. C. D.
5.[2024年广东广州中考真题]函数与的图象如图所示,当( )时,,均随着x的增大而减小.
A. B. C. D.
6.[2024年广东中考真题]方程的解是( )
A. B. C. D.
7.[2024年福建中考真题]如图,已知点A,B在上,,直线与相切,切点为C,且C为的中点,则等于( )
A. B. C. D.
8.[2024年广东东莞中考真题]在中,,,则的值为( )
A. B. C. D.
9.[2024年辽宁中考真题]如图,的对角线,相交于点O,,,若,,则四边形的周长为( )
A.4 B.6 C.8 D.16
10.[2024年湖南中考真题]如图,在中,点D,E分别为边,的中点.下列结论中,错误的是( )
A. B. C. D.
二、填空题(每小题3分,共计30分)
11.[2024年北京中考真题]若在实数范围内有意义,则实数x的取值范围是__________.
12.[2025届·江西抚州·二模]因式分解析:__________.
13.[2024年西藏中考真题]将正比例函数的图象向上平移3个单位长度后得到函数图象的解析式为_________.
14.[2024年湖南长沙中考真题]某乡镇组织“新农村,新气象”春节联欢晚会,进入抽奖环节.抽奖方案如下:不透明的箱子里装有红、黄、蓝三种颜色的球(除颜色外其余都相同),其中红球有2个,黄球有3个,蓝球有5个,每次摇匀后从中随机摸一个球,摸到红球获一等奖,摸到黄球获二等奖,摸到蓝球获三等奖,每个家庭有且只有一次抽奖机会,小明家参与抽奖,获得一等奖的概率为___________.
15.[2024年云南中考真题]若关于x的一元二次方程无实数根,则c的取值范围是________.
16.[2024年广东中考真题]关于x的不等式组中,两个不等式的解集如图所示,则这个不等式组的解集是_______.
17.[2024年江苏淮安中考真题]如图,是的内接三角形,,半径为3,则的长为______.
18.[2024年北京中考真题]如图,在正方形中,点E在上,于点F,于点G.若,,则的面积为__________.
19.[2024年陕西中考真题]已知点和点均在反比例函数的图象上,若,则________0.
20.[2024年浙江中考真题]如图,在菱形中,对角线,相交于点O,.线段与关于过点O的直线l对称,点B的对应点在线段上,交于点E,则与四边形的面积比为___________.
三、解答题(共60分)
21.(7分)[2024年西藏中考真题]先化简,再求值:,请为m选择一个合适的数代入求值.
22.(7分)[2024年湖北武汉中考真题]如图是由小正方形组成的网格,每个小正方形的顶点叫做格点.三个顶点都是格点.仅用无刻度的直尺在给定网格中完成四个画图任务,每个任务的画线不得超过三条.
(1)在图(1)中,画射线交于点D,使平分的面积;
(2)在(1)的基础上,在射线上画点E,使;
(3)在图(2)中,先画点F,使点A绕点F顺时针旋转到点C,再画射线交于点G;
(4)在(3)的基础上,将线段绕点G旋转,画对应线段(点A与点M对应,点B与点N对应).
23.(8分)[2025届·江西抚州·二模]2025年4月24日是第十个“中国航天日”,为迎接中国航天日,某校举行了七、八年级航天知识竞赛,并在七、八年级中各随机抽取了20名学生的竞赛成绩(单位:分.满分100分)进行整理和分析(成绩共分成五组:A.,B.,C.,D.,E.).
【收集、整理数据】
七年级学生竞赛成绩分别为:55,60,67,75,78,78,86,87,87,87,87,88,88,89,90,94,96,98,99,99.
八年级学生竞赛成绩在C组和D组的分别为:72,75,75,75,75,78,85,88,89.
绘制了不完整的统计图.
【分析数据】
两组样本数据的平均数、中位数和众数如下表所示:
年级 平均数 中位数 众数
七年级 84.4 87 b
八年级 81.8 a 75
【问题解决】
请根据上述信息,回答下列问题:
(1)补全频数分布直方图,上表中________,_______,八年级学生成绩D组在扇形统计图中所占扇形的圆心角度数为_______
(2)根据以上数据,你认为此次竞赛该校七年级学生成绩更好,还是八年级学生成绩更好?写出一条理由;
(3)如果该校八年级有600名学生参加此次竞赛,请估计八年级竞赛成绩不低于90分的学生人数.
24.(8分)[2024年湖南中考真题]如图,在四边形中,,点E在边上,.请从“①;②,”这两组条件中任选一组作为已知条件,填在横线上(填序号),再解决下列问题:
(1)求证:四边形为平行四边形;
(2)若,,,求线段的长.
25.(10分)[2024年河南中考真题]为响应“全民植树增绿,共建美丽中国”的号召,学校组织学生到郊外参加义务植树活动,并准备了A,B两种食品作为午餐.这两种食品每包质量均为,营养成分表如下.
(1)若要从这两种食品中摄入热量和蛋白质,应选用A,B两种食品各多少包?
(2)运动量大的人或青少年对蛋白质的摄入量应更多.若每份午餐选用这两种食品共7包,要使每份午餐中的蛋白质含量不低于,且热量最低,应如何选用这两种食品?
26.(10分)[2024年广东东莞中考真题]【概念呈现】设一个钝角三角形的两个锐角为与,如果满足条件,那么我们称这个钝角三角形为倍余三角形,这个锐角叫做倍余角.
(1)【概念理解】当倍余三角形是等腰三角形时,求倍余角的度数;
(2)【拓展探索】如1图,是倍余三角形,是钝角,是倍余角,求证:.
(3)【综合应用】如2图,AB是的直径,点C,D是圆上的两点,弦CD与AB交于点E,连接AC,AD,BD,且,,当是倍余三角形,且为倍余角时,求AD的长.
27.(10分)[2024年山东泰安中考真题]如图,抛物线经过点,与x轴交于点A,点B.
(1)求抛物线的表达式.
(2)将抛物线向右平移1个单位,再向上平移3个单位得到抛物线,求抛物线的表达式,并判断点D是否在抛物线上.
(3)在x轴上方的抛物线上,是否存在点P,使是等腰直角三角形.若存在,请求出点P的坐标;若不存在,请说明理由.
参考答案
1.答案:C
解析:A、不是轴对称图形,故本选项不符合题意;
B、不是轴对称图形,故本选项不符合题意;
C、是轴对称图形,故本选项符合题意;
D、不是轴对称图形,故本选项不符合题意;
故选:C.
2.答案:C
解析:5784亿.
故选:C.
3.答案:B
解析:A.,故该选项不正确,不符合题意;
B.,故该选项正确,符合题意;
C.,故该选项不正确,不符合题意;
D.,故该选项不正确,不符合题意;
故选:B.
4.答案:D
解析:选项A的三视图均不相同,主视图底层是两个正方形,上层是两个正方形;主视图是一列两个正方形俯视图是一行两个正方形,故选项A不符合题意;
选项B的主视图和俯视图相同,底层是两个正方形,上层的左边是一个正方形,左视图的底层是两个正方形,上层的右边是一个正方形,故选项B不符合题意;
选项C的主视图和俯视图相同,底层是两个正方形,上层的右边是一个正方形,左视图的底层是两个正方形,上层的左边是一个正方形,故选项C不符合题意;
选项D的三视图相同,均为底层是两个正方形,上层的左边是一个正方形,故选项D符合题意;
故选:D.
5.答案:D
解析:由函数图象可知,当时,随着x的增大而减小;
位于一、三象限内,且在每一象限内均随着x的增大而减小,
当时,,均随着x的增大而减小,
故选:D.
6.答案:D
解析:,
,
解得:,
检验:当时,,
是原方程的根,
故选:D.
7.答案:A
解析:C为中点,,,,,为的切线,,.故选A.
8.答案:D
解析:如图,
在中,,
设,则,
,
,
故选:D.
9.答案:C
解析:四边形是平行四边形,
,,
,,
四边形是平行四边形,
,,
周长为:,
故选:C.
10.答案:D
解析:点D,E分别为边,的中点,
,,故A、C正确;
,
,故B正确;
,
,
,故D错误;
故选:D.
11.答案:
解析:根据题意得,
解得:.
故答案为:.
12.答案:
解析:
,
故答案为:.
13.答案:
解析:正比例函数的图象向上平移3个单位长度后得到函数图象的解析式为:,
故答案为:.
14.答案:
解析:小明家参与抽奖,获得一等奖的概率为,
故答案为:.
15.答案:
解析:根据题意得,
解得.
故答案为:.
16.答案:
解析:由数轴可知,两个不等式的解集分别为,,
不等式组的解集为,故答案为.
17.答案:
解析:,
,
弧BC的长为:.
故答案为:.
18.答案:
解析:根据正方形的性质,得,,
,
,
,
,
,
,
,
,
的面积为;
故答案为:.
19.答案:<
解析:点和点均在反比例函数的图象上,
,,
,
,
.
故答案为:<.
20.答案:/
解析:四边形是菱形,,
设,,
,,
如图所示,连接,,直线l交于点F,交于点G,
线段与关于过点O的直线l对称,点B的对应点在线段上,
,,,
,
点,D,O三点共线
,,
,
,
,
,
由对称可得,,
,
,
又,
,
,
,
又,,
,
,
.
故答案为:.
21.答案:,取,原式
解析:
,
∵,,
∴,,
∴取,原式.
22.答案:(1)作图见解析
(2)作图见解析
(3)作图见解析
(4)作图见解析
解析:(1)如图所示,点D即为所求.
(2)如图所示,点E即为所求.
(3)如图所示.
(4)如图所示.
23.答案:(1)81.5,87,54
(2)七年级学生成绩更好,见解析
(3)210人
解析:七年级抽取的20名学生的竞赛成绩在组D的人数为(人),
∴补全频数分布直方图如图:
根据扇形统计图得,八年级学生成绩在组的有(人)
八年级学生成绩排在第的是,
;
七年级学生竞赛成绩最多的是87,有4个
;
八年级学生成绩D组在扇形统计图中所占的扇形的圆心角度数为,
故答案为:81.5,87,54.
(2)解析:七年级学生成绩更好,
七年级的平均成绩更高(答案不唯一).
(3)解析:(人).
答:估计八年级竞赛成绩不低于90分的学生人数为210人.
24.答案:(1)①或②,证明见解析
(2)6
解析:(1)选择①,证明:,
,
,
四边形为平行四边形;
选择②,证明:,,
,
,
四边形为平行四边形;
(2)由(1)得,
,,
.
25.答案:(1)选用A种食品4包,B种食品2包
(2)选用A种食品3包,B种食品4包
解析:(1)设选用A种食品x包,B种食品y包
根据题意,得
解得.
答:选用A种食品4包,B种食品2包.
(2)设选用A种食品m包,则选用B种食品包,
根据题意,得.
解得.
设每份午餐的总热量为,则
,随m的增大而减小.
当时,w取得最小值,此时.
答:选用A种食品3包,B种食品4包.
26.答案:(1)
(2)证明见解析
(3)
解析:(1)设倍余角的度数为x,
∵倍余三角形是等腰三角形,∴另一个锐角度数为x,
∴,
∴,
∴当倍余三角形是等腰三角形时,倍余角的度数为.
(2)证明:如图1,作交AC于D,
是倍余三角形,是钝角,是倍余角,
,
,
,
,
.
(3)如图,当是倍余三角形,且为倍余角时,
,,
,,
,是倍余三角形,且为倍余角,
是直径,
,
由(2)得,
,
当是倍余三角形,且为倍余角时,
,,
,
即,
,
,
,
,,
,
作于H,
,
,,
,
,
,
.
27.答案:(1)
(2),点D在抛物线上
(3)存在,点P的坐标为或
解析:(1)抛物线经过点,
,解得,
抛物线的表达式为.
(2)将抛物线向右平移1个单位,再向上平移3个单位得到抛物线,
抛物线.
当时,,
故点D在抛物线上.
(3)存在.
分三种情况讨论.
①当为直角时,点P在y轴右侧抛物线上,如图(1),过点D作直线轴,过点B作于点G,过点P作于点H.
对于,令,得,得,,,.
,,
.
又,,
,
,,
.
当时,,
点P在抛物线上,满足题意.
②当为直角时,点P在y轴左侧抛物线上,如图(2),过点B作直线轴,过点D作于点M,过点P作于点N,
同理可证,
,,
.
当时,,
点P在抛物线上.
③当为直角时,如图(3),过点P作直线轴,过点B作于点K,过点D作于点R,设.
同理可证,
,,即,.
解得,,.
当时,,
此时点P不在抛物线上.
综上,点P的坐标为或.
【满分:120分】
一、选择题(每小题3分,共计30分)
1.[2024年重庆中考真题]下列四种化学仪器的示意图中,是轴对称图形的是( )
A. B. C. D.
2.[2024年河南中考真题]据统计,2023年我国人工智能核心产业规模达5784亿元,数据“5784亿”用科学记数法表示为( )
A. B. C. D.
3.[2024年湖北武汉中考真题]下列计算正确的是( )
A. B. C. D.
4.[2024年山东威海中考真题]下列几何体都是由四个大小相同的小正方体搭成的.其中主视图,左视图和俯视图完全相同的是( )
A. B. C. D.
5.[2024年广东广州中考真题]函数与的图象如图所示,当( )时,,均随着x的增大而减小.
A. B. C. D.
6.[2024年广东中考真题]方程的解是( )
A. B. C. D.
7.[2024年福建中考真题]如图,已知点A,B在上,,直线与相切,切点为C,且C为的中点,则等于( )
A. B. C. D.
8.[2024年广东东莞中考真题]在中,,,则的值为( )
A. B. C. D.
9.[2024年辽宁中考真题]如图,的对角线,相交于点O,,,若,,则四边形的周长为( )
A.4 B.6 C.8 D.16
10.[2024年湖南中考真题]如图,在中,点D,E分别为边,的中点.下列结论中,错误的是( )
A. B. C. D.
二、填空题(每小题3分,共计30分)
11.[2024年北京中考真题]若在实数范围内有意义,则实数x的取值范围是__________.
12.[2025届·江西抚州·二模]因式分解析:__________.
13.[2024年西藏中考真题]将正比例函数的图象向上平移3个单位长度后得到函数图象的解析式为_________.
14.[2024年湖南长沙中考真题]某乡镇组织“新农村,新气象”春节联欢晚会,进入抽奖环节.抽奖方案如下:不透明的箱子里装有红、黄、蓝三种颜色的球(除颜色外其余都相同),其中红球有2个,黄球有3个,蓝球有5个,每次摇匀后从中随机摸一个球,摸到红球获一等奖,摸到黄球获二等奖,摸到蓝球获三等奖,每个家庭有且只有一次抽奖机会,小明家参与抽奖,获得一等奖的概率为___________.
15.[2024年云南中考真题]若关于x的一元二次方程无实数根,则c的取值范围是________.
16.[2024年广东中考真题]关于x的不等式组中,两个不等式的解集如图所示,则这个不等式组的解集是_______.
17.[2024年江苏淮安中考真题]如图,是的内接三角形,,半径为3,则的长为______.
18.[2024年北京中考真题]如图,在正方形中,点E在上,于点F,于点G.若,,则的面积为__________.
19.[2024年陕西中考真题]已知点和点均在反比例函数的图象上,若,则________0.
20.[2024年浙江中考真题]如图,在菱形中,对角线,相交于点O,.线段与关于过点O的直线l对称,点B的对应点在线段上,交于点E,则与四边形的面积比为___________.
三、解答题(共60分)
21.(7分)[2024年西藏中考真题]先化简,再求值:,请为m选择一个合适的数代入求值.
22.(7分)[2024年湖北武汉中考真题]如图是由小正方形组成的网格,每个小正方形的顶点叫做格点.三个顶点都是格点.仅用无刻度的直尺在给定网格中完成四个画图任务,每个任务的画线不得超过三条.
(1)在图(1)中,画射线交于点D,使平分的面积;
(2)在(1)的基础上,在射线上画点E,使;
(3)在图(2)中,先画点F,使点A绕点F顺时针旋转到点C,再画射线交于点G;
(4)在(3)的基础上,将线段绕点G旋转,画对应线段(点A与点M对应,点B与点N对应).
23.(8分)[2025届·江西抚州·二模]2025年4月24日是第十个“中国航天日”,为迎接中国航天日,某校举行了七、八年级航天知识竞赛,并在七、八年级中各随机抽取了20名学生的竞赛成绩(单位:分.满分100分)进行整理和分析(成绩共分成五组:A.,B.,C.,D.,E.).
【收集、整理数据】
七年级学生竞赛成绩分别为:55,60,67,75,78,78,86,87,87,87,87,88,88,89,90,94,96,98,99,99.
八年级学生竞赛成绩在C组和D组的分别为:72,75,75,75,75,78,85,88,89.
绘制了不完整的统计图.
【分析数据】
两组样本数据的平均数、中位数和众数如下表所示:
年级 平均数 中位数 众数
七年级 84.4 87 b
八年级 81.8 a 75
【问题解决】
请根据上述信息,回答下列问题:
(1)补全频数分布直方图,上表中________,_______,八年级学生成绩D组在扇形统计图中所占扇形的圆心角度数为_______
(2)根据以上数据,你认为此次竞赛该校七年级学生成绩更好,还是八年级学生成绩更好?写出一条理由;
(3)如果该校八年级有600名学生参加此次竞赛,请估计八年级竞赛成绩不低于90分的学生人数.
24.(8分)[2024年湖南中考真题]如图,在四边形中,,点E在边上,.请从“①;②,”这两组条件中任选一组作为已知条件,填在横线上(填序号),再解决下列问题:
(1)求证:四边形为平行四边形;
(2)若,,,求线段的长.
25.(10分)[2024年河南中考真题]为响应“全民植树增绿,共建美丽中国”的号召,学校组织学生到郊外参加义务植树活动,并准备了A,B两种食品作为午餐.这两种食品每包质量均为,营养成分表如下.
(1)若要从这两种食品中摄入热量和蛋白质,应选用A,B两种食品各多少包?
(2)运动量大的人或青少年对蛋白质的摄入量应更多.若每份午餐选用这两种食品共7包,要使每份午餐中的蛋白质含量不低于,且热量最低,应如何选用这两种食品?
26.(10分)[2024年广东东莞中考真题]【概念呈现】设一个钝角三角形的两个锐角为与,如果满足条件,那么我们称这个钝角三角形为倍余三角形,这个锐角叫做倍余角.
(1)【概念理解】当倍余三角形是等腰三角形时,求倍余角的度数;
(2)【拓展探索】如1图,是倍余三角形,是钝角,是倍余角,求证:.
(3)【综合应用】如2图,AB是的直径,点C,D是圆上的两点,弦CD与AB交于点E,连接AC,AD,BD,且,,当是倍余三角形,且为倍余角时,求AD的长.
27.(10分)[2024年山东泰安中考真题]如图,抛物线经过点,与x轴交于点A,点B.
(1)求抛物线的表达式.
(2)将抛物线向右平移1个单位,再向上平移3个单位得到抛物线,求抛物线的表达式,并判断点D是否在抛物线上.
(3)在x轴上方的抛物线上,是否存在点P,使是等腰直角三角形.若存在,请求出点P的坐标;若不存在,请说明理由.
参考答案
1.答案:C
解析:A、不是轴对称图形,故本选项不符合题意;
B、不是轴对称图形,故本选项不符合题意;
C、是轴对称图形,故本选项符合题意;
D、不是轴对称图形,故本选项不符合题意;
故选:C.
2.答案:C
解析:5784亿.
故选:C.
3.答案:B
解析:A.,故该选项不正确,不符合题意;
B.,故该选项正确,符合题意;
C.,故该选项不正确,不符合题意;
D.,故该选项不正确,不符合题意;
故选:B.
4.答案:D
解析:选项A的三视图均不相同,主视图底层是两个正方形,上层是两个正方形;主视图是一列两个正方形俯视图是一行两个正方形,故选项A不符合题意;
选项B的主视图和俯视图相同,底层是两个正方形,上层的左边是一个正方形,左视图的底层是两个正方形,上层的右边是一个正方形,故选项B不符合题意;
选项C的主视图和俯视图相同,底层是两个正方形,上层的右边是一个正方形,左视图的底层是两个正方形,上层的左边是一个正方形,故选项C不符合题意;
选项D的三视图相同,均为底层是两个正方形,上层的左边是一个正方形,故选项D符合题意;
故选:D.
5.答案:D
解析:由函数图象可知,当时,随着x的增大而减小;
位于一、三象限内,且在每一象限内均随着x的增大而减小,
当时,,均随着x的增大而减小,
故选:D.
6.答案:D
解析:,
,
解得:,
检验:当时,,
是原方程的根,
故选:D.
7.答案:A
解析:C为中点,,,,,为的切线,,.故选A.
8.答案:D
解析:如图,
在中,,
设,则,
,
,
故选:D.
9.答案:C
解析:四边形是平行四边形,
,,
,,
四边形是平行四边形,
,,
周长为:,
故选:C.
10.答案:D
解析:点D,E分别为边,的中点,
,,故A、C正确;
,
,故B正确;
,
,
,故D错误;
故选:D.
11.答案:
解析:根据题意得,
解得:.
故答案为:.
12.答案:
解析:
,
故答案为:.
13.答案:
解析:正比例函数的图象向上平移3个单位长度后得到函数图象的解析式为:,
故答案为:.
14.答案:
解析:小明家参与抽奖,获得一等奖的概率为,
故答案为:.
15.答案:
解析:根据题意得,
解得.
故答案为:.
16.答案:
解析:由数轴可知,两个不等式的解集分别为,,
不等式组的解集为,故答案为.
17.答案:
解析:,
,
弧BC的长为:.
故答案为:.
18.答案:
解析:根据正方形的性质,得,,
,
,
,
,
,
,
,
,
的面积为;
故答案为:.
19.答案:<
解析:点和点均在反比例函数的图象上,
,,
,
,
.
故答案为:<.
20.答案:/
解析:四边形是菱形,,
设,,
,,
如图所示,连接,,直线l交于点F,交于点G,
线段与关于过点O的直线l对称,点B的对应点在线段上,
,,,
,
点,D,O三点共线
,,
,
,
,
,
由对称可得,,
,
,
又,
,
,
,
又,,
,
,
.
故答案为:.
21.答案:,取,原式
解析:
,
∵,,
∴,,
∴取,原式.
22.答案:(1)作图见解析
(2)作图见解析
(3)作图见解析
(4)作图见解析
解析:(1)如图所示,点D即为所求.
(2)如图所示,点E即为所求.
(3)如图所示.
(4)如图所示.
23.答案:(1)81.5,87,54
(2)七年级学生成绩更好,见解析
(3)210人
解析:七年级抽取的20名学生的竞赛成绩在组D的人数为(人),
∴补全频数分布直方图如图:
根据扇形统计图得,八年级学生成绩在组的有(人)
八年级学生成绩排在第的是,
;
七年级学生竞赛成绩最多的是87,有4个
;
八年级学生成绩D组在扇形统计图中所占的扇形的圆心角度数为,
故答案为:81.5,87,54.
(2)解析:七年级学生成绩更好,
七年级的平均成绩更高(答案不唯一).
(3)解析:(人).
答:估计八年级竞赛成绩不低于90分的学生人数为210人.
24.答案:(1)①或②,证明见解析
(2)6
解析:(1)选择①,证明:,
,
,
四边形为平行四边形;
选择②,证明:,,
,
,
四边形为平行四边形;
(2)由(1)得,
,,
.
25.答案:(1)选用A种食品4包,B种食品2包
(2)选用A种食品3包,B种食品4包
解析:(1)设选用A种食品x包,B种食品y包
根据题意,得
解得.
答:选用A种食品4包,B种食品2包.
(2)设选用A种食品m包,则选用B种食品包,
根据题意,得.
解得.
设每份午餐的总热量为,则
,随m的增大而减小.
当时,w取得最小值,此时.
答:选用A种食品3包,B种食品4包.
26.答案:(1)
(2)证明见解析
(3)
解析:(1)设倍余角的度数为x,
∵倍余三角形是等腰三角形,∴另一个锐角度数为x,
∴,
∴,
∴当倍余三角形是等腰三角形时,倍余角的度数为.
(2)证明:如图1,作交AC于D,
是倍余三角形,是钝角,是倍余角,
,
,
,
,
.
(3)如图,当是倍余三角形,且为倍余角时,
,,
,,
,是倍余三角形,且为倍余角,
是直径,
,
由(2)得,
,
当是倍余三角形,且为倍余角时,
,,
,
即,
,
,
,
,,
,
作于H,
,
,,
,
,
,
.
27.答案:(1)
(2),点D在抛物线上
(3)存在,点P的坐标为或
解析:(1)抛物线经过点,
,解得,
抛物线的表达式为.
(2)将抛物线向右平移1个单位,再向上平移3个单位得到抛物线,
抛物线.
当时,,
故点D在抛物线上.
(3)存在.
分三种情况讨论.
①当为直角时,点P在y轴右侧抛物线上,如图(1),过点D作直线轴,过点B作于点G,过点P作于点H.
对于,令,得,得,,,.
,,
.
又,,
,
,,
.
当时,,
点P在抛物线上,满足题意.
②当为直角时,点P在y轴左侧抛物线上,如图(2),过点B作直线轴,过点D作于点M,过点P作于点N,
同理可证,
,,
.
当时,,
点P在抛物线上.
③当为直角时,如图(3),过点P作直线轴,过点B作于点K,过点D作于点R,设.
同理可证,
,,即,.
解得,,.
当时,,
此时点P不在抛物线上.
综上,点P的坐标为或.
同课章节目录
