2025届中考数学全真模拟卷 【河北专用】(含详解)
文档属性
| 名称 | 2025届中考数学全真模拟卷 【河北专用】(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-07 08:47:21 | ||
图片预览




文档简介
2025届中考数学全真模拟卷 【河北专用】
【满分120分】
一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.[2024年广西中考真题]下列选项记录了我国四个直辖市某年一月份的平均气温,其中气温最低的是( )
A.北京 B.上海 C.天津 D.重庆
2.[2024年吉林长春中考真题]南湖公园是长春市著名旅游景点之一,图①是公园中“四角亭”景观的照片,图②是其航拍照片,则图③是“四角亭”景观的( )
A.主视图 B.俯视图 C.左视图 D.右视图
3.[2024年江西中考真题]“长征是宣言书,长征是宣传队,长征是播种机”.二万五千里长征是中国史上的伟大壮举,也是人类史上的奇迹,25000用科学记数法可表示为( )
A. B. C. D.
4.[2025届·河北张家口·一模]若a,b是正整数,且满足,则下列a与b关系正确的是( )
A. B. C. D.
5.[2024年福建中考真题]在同一平面内,将直尺、含角的三角尺和木工角尺按如图方式摆放,若,则的大小为( )
A. B. C. D.
6.[2024年江苏淮安中考真题]如图,用9个直角三角形纸片拼成一个类似海螺的图形,其中每一个直角三角形都有一条直角边长为1记这个图形的周长(实线部分)为l,则下列整数与l最接近的是( )
A.14 B.13 C.12 D.11
7.[2024年湖北中考真题]《九章算术》中记载这样一个题:牛5头和羊2只共值10金,牛2头和羊5只共值8金,问牛和羊各值多少金?设每头牛值x金,每只羊值y金,可列方程为( )
A. B. C. D.
8.[2024年河南中考真题]豫剧是国家级非物质文化遗产,因其雅俗共赏,深受大众喜爱.正面印有豫剧经典剧目人物的三张卡片如图所示,它们除正面外完全相同.把这三张卡片背面朝上洗匀,从中随机抽取一张,放回洗匀后,再从中随机抽取一张,两次抽取的卡片正面相同的概率为( )
A. B. C. D.
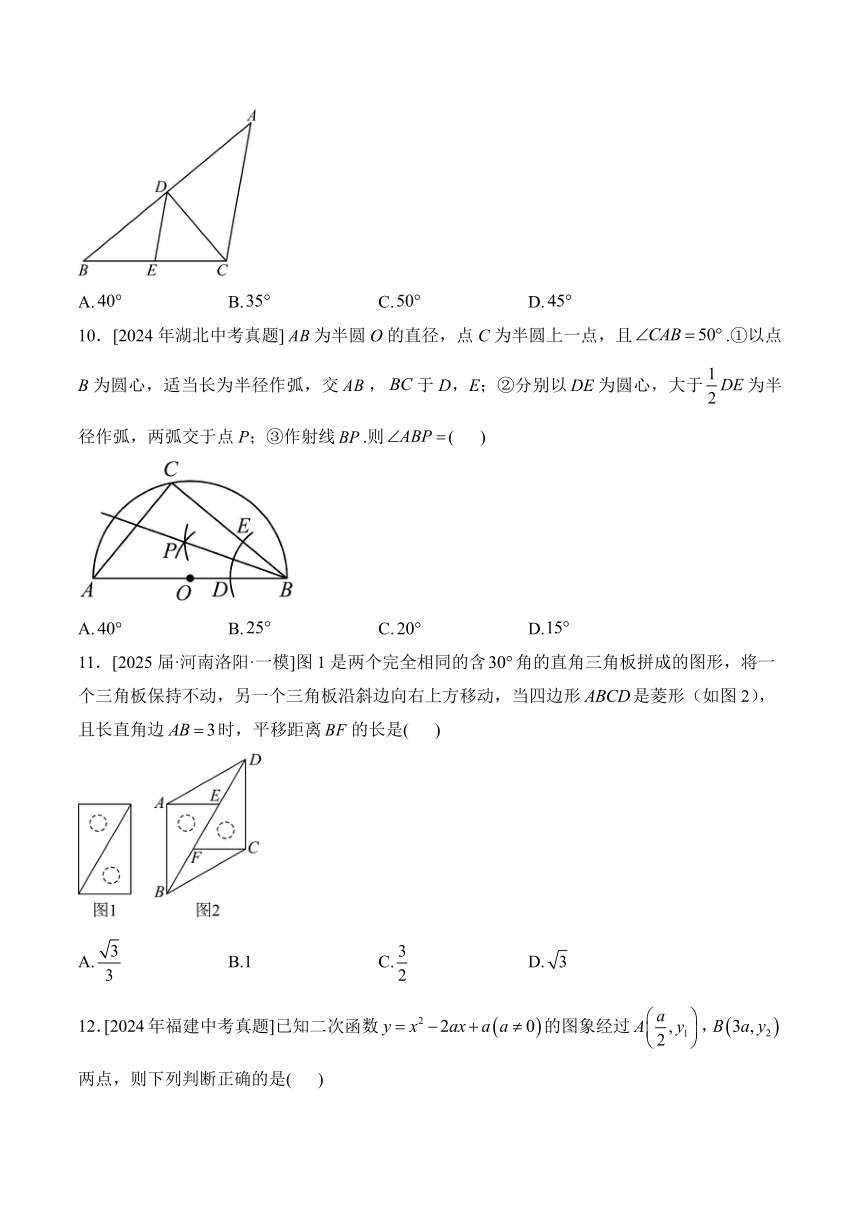
9.[2025届·河南郑州·一模]如图,在等腰中,,点D是边上的中点,,交于点E.若,则的度数是( )
A. B. C. D.
10.[2024年湖北中考真题]为半圆O的直径,点C为半圆上一点,且.①以点B为圆心,适当长为半径作弧,交,于D,E;②分别以为圆心,大于为半径作弧,两弧交于点P;③作射线.则( )
A. B. C. D.
11.[2025届·河南洛阳·一模]图1是两个完全相同的含角的直角三角板拼成的图形,将一个三角板保持不动,另一个三角板沿斜边向右上方移动,当四边形是菱形(如图2),且长直角边时,平移距离的长是( )
A. B.1 C. D.
12.[2024年福建中考真题]已知二次函数的图象经过,两点,则下列判断正确的是( )
A.可以找到一个实数a,使得 B.无论实数a取什么值,都有
C.可以找到一个实数a,使得 D.无论实数a取什么值,都有
二、填空题(本大题共4小题,每小题3分,共12分.请把答案填在题中横线上)
13.[2024年北京中考真题]方程的解为__________.
14.[2025届·河北石家庄·一模]若关于x的一元二次方程的一个根为,则另一个根为________.
15.[2024年广东东莞中考真题]点D是锐角内一点,于点E,点F是线段OE的一个动点,点G是射线OB的一个动点,连接DF、FG、GD,当的周长最小时,与的数量关系式是________
16.[2024年广东广州中考真题]如图,平面直角坐标系中,矩形的顶点B在函数的图象上,,.将线段沿x轴正方向平移得线段(点A平移后的对应点为),交函数的图象于点D,过点D作轴于点E,则下列结论:
①;
②的面积等于四边形的面积;
③的最小值是;
④.
其中正确的结论有______.(填写所有正确结论的序号)
三、解答题(本大题共8小题,共72分.解答应写出必要的文字说明,证明过程或演算步骤)
17.(7分)[2025届·河北石家庄·一模]一个三位数,如果十位数字恰好等于百位数字与个位数字之和的一半,我们称这个三位数为“半和数”.例如,因为,所以是半和数.
(1)已知是半和数,若,,求c的值;
(2)嘉嘉认为任意一个半和数都能被3整除.你同意嘉嘉的看法吗?说明理由.
18.(8分)[2024年山东威海中考真题]定义:我们把数轴上表示数a的点与原点的距离叫做数a的绝对值.数轴上表示数a,b的点A,B之间的距离.特别的,当时,表示数a的点与原点的距离等于.当时,表示数a的点与原点的距离等于.
应用:如图,在数轴上,动点A从表示的点出发,以1个单位长度/秒的速度沿着数轴的正方向运动.同时,动点B从表示12的点出发,以2个单位长度/秒的速度沿着数轴的负方向运动.
(1)经过多长时间,点A,B之间的距离等于3个单位长度?
(2)求点A,B到原点距离之和的最小值.
19.(8分)[2024年山东泰安中考真题]某超市打算购进一批苹果,现从甲、乙两个供应商供应的苹果中各随机抽取10个,测得它们的直径(单位:),并制作统计图如下:
根据以上信息,解答下列问题:
(1)
统计量供应商 平均数 中位数 众数
甲 80 80 b
乙 m a 76
则____________,____________,____________.
(2)苹果直径的方差越小,苹果的大小越整齐,据此判断,____________供应商供应的苹果大小更为整齐.(填“甲”或“乙”)
(3)超市规定直径(含)以上的苹果为大果,超市打算购进甲供应商的苹果3500个,那么大果约有多少个?
20.(8分)[2024年广西中考真题]如图,已知是的外接圆,.点D,E分别是,的中点,连接并延长至点F,使,连接.
(1)求证:四边形是平行四边形;
(2)求证:与相切;
(3)若,,求的半径.
21.(9分)[2024年北京中考真题]在平面直角坐标系中,函数与的图象交于点.
(1)求k,b的值;
(2)当时,对于x的每一个值,函数的值既大于函数的值,也大于函数的值,直接写出m的取值范围.
22.(9分)[2024年广东中考真题]中国新能源汽车为全球应对气候变化和绿色低碳转型作出了巨大贡献.为满足新能源汽车的充电需求,某小区增设了充电站,如图是矩形PQMN充电站的平面示意图,矩形ABCD是其中一个停车位.经测量,,,,,GH是另一个车位的宽,所有车位的长宽相同,按图示并列划定.
根据以上信息回答下列问题:(结果精确到0.1m,参考数据)
(1)求PQ的长;
(2)该充电站有20个停车位,求PN的长.
23.(11分)[2024年江苏淮安中考真题]二次函数的图像经过点,顶点为P.
(1)______;
(2)当时,
①若顶点P到x轴的距离为10,则______;
②直线m过点且垂直于y轴,顶点P到直线m的距离为h,随着b的增大,h的值如何变化?请描述变化过程,并说明理由;
(3)若二次函数图像交x轴于B、C两点,点B坐标为,且的面积不小于20,求a的取值范围.
24.(12分)[2025届·河南郑州·一模]如图1,在矩形中,,,连接,与重合,将绕点A顺时针方向旋转,连接,.
(1)旋转过程中一定是等腰三角形的三角形有______,的值为______.
(2)如图2,当点E落在对角线上时,求的长.
(3)连接,试探究能否构成以为直角边的,若能,直接写出线段的长;若不能,请说明理由.
参考答案
1.答案:A
解析:因为,所以气温最低的是北京,故选A.
2.答案:B
解析:由题意可知图③是从“四角亭”上方看到的,即为俯视图.
故选B.
3.答案:C
解析:;
故选:C.
4.答案:D
解析:,
,
,
,
.
故选:D.
5.答案:A
解析:,
,
,
,
故选:A.
6.答案:B
解析:第一个三角形的斜边长,
第二个三角形的斜边长
第九个三角形的斜边长
则这海螺图形周长
与最接近的整数是3,
与最接近的整数是13,
故选:B.
7.答案:A
解析:设每头牛值x金,每头羊值y金,牛5头,羊2头,共值10金;牛2头,羊5头,共值8金,,故选:A.
8.答案:D
解析:将三张卡片分别记为A,B,C,
列表如下:
A B C
A
B
C
共有9种等可能的结果,其中两次抽取的卡片,正面相同的结果有3种,
两次抽取的卡片正面相同的概率为.
故选:D.
9.答案:C
解析:∵,,
∴,
∴,
∵,点D是边上的中点,
∴,
∵,
∴,
故选:C.
10.答案:C
解析:为半圆O的直径,,,,由作图知,是的角平分线,,故选:C.
11.答案:D
解析:由题意得,
∴
∵四边形是菱形,
∴,
∴,
∴,
∴,
∴,
在中,,
∴,
即平移距离,
故选:D.
12.答案:C
解析:二次函数解析式为,
二次函数开口向上,且对称轴为
顶点坐标为.
当时,
当时,.
故A、B错误,不符合题意;
当时,,由二次函数对称性可知点和点关于对称轴对称,在对称轴右侧,y随z的增大而增大,所以当时,;
当时,,由二次函数对称性可知可知点和点关于对称轴对称,在对称轴左侧,y随z的增大而减小,所以当时不一定大于0,
故C正确,符合题意;D错误,不符合题意;故选:C.
13.答案:
解析:
,
解得:,
经检验:是原方程的解,
所以,原方程的解为,
故答案为:.
14.答案:3
解析:设该方程的另一个根为,
由题意可得:,
∴,
∴另一个根为,
故答案为:.
15.答案:
解析:作D关于OA的对称点,
作D关于OB的对称得,
连接,交OA、OB于F、G,
此时的周长最小,
最小值为,连、、,
由轴对称的性质可知,,,
,,,,
,,
,
,
故答案为.
16.答案:①②④
解析:,,四边形是矩形;
,
,故①符合题意;
如图,连接,,,与的交点为K,
,
,
,
的面积等于四边形的面积;故②符合题意;
如图,连接,
轴,,
四边形为矩形,
,
当最小,则最小,
设,
,
,
的最小值为2,故③不符合题意;
如图,设平移距离为n,
,
反比例函数为,四边形为矩形,
,,
,,,,
,
,
,
,
,
,故④符合题意;
故答案为:①②④.
17.答案:(1)5
(2)同意;理由见解析
解析:∵是“半和数”,∴.
∵,,
∴.
∴;
(2)同意.
设是一个“半和数”,则.
∴.
∵a,c整数,
∴为整数.
∴任意一个“半和数”都能被3整除.
18.答案:(1)4秒或6秒
(2)3
解析:(1)设运动时间为x秒,则点A表示的数为,点B表示的数为,
根据题意,得,
解得或6.
答:经过4秒或6秒,点A,B之间的距离等于3个单位长度.
(2)由(1)知,点A,B到原点距离之和为.
当时,.
,,即.
当时,.
,,即.
当时,.
,,即.
综上可知,点A,B到原点距离之和的最小值为3.
19.答案:(1)80,,83
(2)甲
(3)1050
解析:(1),
对乙的10个数据进行排序为:75,76,76,76,79,80,81,83,86,88,
所以,中位数为,
通过观察甲的数据可知83出现的次数最多,故众数.
故答案为:80,,83.
(2)
所以,甲的方差比乙的方差小,
故答案为:甲.
(3)(个)
所以,大果约有1050个.
20.答案:(1)证明见解析
(2)证明见解析
(3)10
解析:(1)证明:点D,E分别是,的中点,
,,
又,,
,
,,
,,
四边形是平行四边形;
(2)证明:如图,连接,
,D为中点,
,
过圆心,
,
,
而为半径,
为的切线;
(3)如图,过B作于Q,连接,
,
,
设,则,
,
,
,
,
,
,
,,,
,
,
设半径为r,
,
,
解得:,
的半径为10.
21.答案:(1),
(2)
解析:(1)由题意得将代入得:,
解得:,
将,,代入函数中,
得:,
解得:,
,;
(2),,
两个一次函数的解析式分别为,,
当时,对于x的每一个值,函数的值既大于函数的值,也大于函数的值,
即当时,对于x的每一个值,直线的图像在直线和直线的上方,则画出图象为:
由图象得:当直线与直线平行时符合题意或者当与x轴的夹角大于直线与直线平行时的夹角也符合题意,
当直线与直线平行时,,
当时,对于x的每一个值,直线的图像在直线和直线的上方时,,
m的取值范围为.
22.答案:(1)6.1m
(2)66.7m
解析:(1)四边形PQMN是矩形,
,
在中,,,
,,
四边形ABCD是矩形,
,,
,
,
,
,
,
.
(2)中,,
在中,,
该充电站有20个停车位,
,
四边形ABCD是矩形,
.
23.答案:(1)8
(2)①
②见解析
(3)或且
解析:(1)将点A坐标代入抛物线表达式得:
故答案为:8;
(2)①当时,抛物线的表达式为:
,
则,
即,
解得:,
故答案为:;
②顶点P的纵坐标为:,
则,
令,则或,
函数h的大致图象如下:
从图象看,当或时,h随b的最大而增大,当或时,h随b的增大而减小;
(3)设点C、B的横坐标为m,n,
将点B的坐标代入抛物线得:,
则,
即抛物线的表达式为:,
则,,
则,
则的面积,
即,
则或,
解得:或且.
24.答案:(1),,
(2)的长为或
(3)能,或,理由见解析
解析:(1)∵四边形是矩形,,,
∴,,,
∴,
∵与重合,
∴,,,,
∴将绕点A顺时针方向旋转时,,,
∴,是等腰三角形,
∵旋转,
∴,
又,
∴,
∴,
故答案为:,,;
(2)第一种情况,如图所示,点E在上时,
∴,,,
∴,
在中,,
由(1)可得,,
∴;
第二种情况,如图所示,点E在延长线时,
∴,
在中,,
∵,
∴,即,
∴;
综上所述,的长为或;
(3)能,或,理由如下,
第一种情况,如图所示,,是以为直角边的三角形,
由(1)可得,,,
∴设,,
∵旋转,
∴,,,
∴是等腰三角形,
过点A作于点H,交于点K,
∴,
∵,
∴,
∴,
∴,
∴点K是的中点,
∴,
在中,,
∴,
在中,,,
∴,
∴,
在中,,点K是中点,
∴,
在中,,
∴,
整理得,,
解得,(负值舍去),
∴;
第二种情况,如图所示,,是以为直角边的三角形,
∵与重合,
∴,,,,
∴,是等腰三角形,
∴,
过点A作与点G,
∴,,
∴四边形是矩形,
∴,
∴;
综上所述,能构成以为直角边的,线段的长为或6.
【满分120分】
一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.[2024年广西中考真题]下列选项记录了我国四个直辖市某年一月份的平均气温,其中气温最低的是( )
A.北京 B.上海 C.天津 D.重庆
2.[2024年吉林长春中考真题]南湖公园是长春市著名旅游景点之一,图①是公园中“四角亭”景观的照片,图②是其航拍照片,则图③是“四角亭”景观的( )
A.主视图 B.俯视图 C.左视图 D.右视图
3.[2024年江西中考真题]“长征是宣言书,长征是宣传队,长征是播种机”.二万五千里长征是中国史上的伟大壮举,也是人类史上的奇迹,25000用科学记数法可表示为( )
A. B. C. D.
4.[2025届·河北张家口·一模]若a,b是正整数,且满足,则下列a与b关系正确的是( )
A. B. C. D.
5.[2024年福建中考真题]在同一平面内,将直尺、含角的三角尺和木工角尺按如图方式摆放,若,则的大小为( )
A. B. C. D.
6.[2024年江苏淮安中考真题]如图,用9个直角三角形纸片拼成一个类似海螺的图形,其中每一个直角三角形都有一条直角边长为1记这个图形的周长(实线部分)为l,则下列整数与l最接近的是( )
A.14 B.13 C.12 D.11
7.[2024年湖北中考真题]《九章算术》中记载这样一个题:牛5头和羊2只共值10金,牛2头和羊5只共值8金,问牛和羊各值多少金?设每头牛值x金,每只羊值y金,可列方程为( )
A. B. C. D.
8.[2024年河南中考真题]豫剧是国家级非物质文化遗产,因其雅俗共赏,深受大众喜爱.正面印有豫剧经典剧目人物的三张卡片如图所示,它们除正面外完全相同.把这三张卡片背面朝上洗匀,从中随机抽取一张,放回洗匀后,再从中随机抽取一张,两次抽取的卡片正面相同的概率为( )
A. B. C. D.
9.[2025届·河南郑州·一模]如图,在等腰中,,点D是边上的中点,,交于点E.若,则的度数是( )
A. B. C. D.
10.[2024年湖北中考真题]为半圆O的直径,点C为半圆上一点,且.①以点B为圆心,适当长为半径作弧,交,于D,E;②分别以为圆心,大于为半径作弧,两弧交于点P;③作射线.则( )
A. B. C. D.
11.[2025届·河南洛阳·一模]图1是两个完全相同的含角的直角三角板拼成的图形,将一个三角板保持不动,另一个三角板沿斜边向右上方移动,当四边形是菱形(如图2),且长直角边时,平移距离的长是( )
A. B.1 C. D.
12.[2024年福建中考真题]已知二次函数的图象经过,两点,则下列判断正确的是( )
A.可以找到一个实数a,使得 B.无论实数a取什么值,都有
C.可以找到一个实数a,使得 D.无论实数a取什么值,都有
二、填空题(本大题共4小题,每小题3分,共12分.请把答案填在题中横线上)
13.[2024年北京中考真题]方程的解为__________.
14.[2025届·河北石家庄·一模]若关于x的一元二次方程的一个根为,则另一个根为________.
15.[2024年广东东莞中考真题]点D是锐角内一点,于点E,点F是线段OE的一个动点,点G是射线OB的一个动点,连接DF、FG、GD,当的周长最小时,与的数量关系式是________
16.[2024年广东广州中考真题]如图,平面直角坐标系中,矩形的顶点B在函数的图象上,,.将线段沿x轴正方向平移得线段(点A平移后的对应点为),交函数的图象于点D,过点D作轴于点E,则下列结论:
①;
②的面积等于四边形的面积;
③的最小值是;
④.
其中正确的结论有______.(填写所有正确结论的序号)
三、解答题(本大题共8小题,共72分.解答应写出必要的文字说明,证明过程或演算步骤)
17.(7分)[2025届·河北石家庄·一模]一个三位数,如果十位数字恰好等于百位数字与个位数字之和的一半,我们称这个三位数为“半和数”.例如,因为,所以是半和数.
(1)已知是半和数,若,,求c的值;
(2)嘉嘉认为任意一个半和数都能被3整除.你同意嘉嘉的看法吗?说明理由.
18.(8分)[2024年山东威海中考真题]定义:我们把数轴上表示数a的点与原点的距离叫做数a的绝对值.数轴上表示数a,b的点A,B之间的距离.特别的,当时,表示数a的点与原点的距离等于.当时,表示数a的点与原点的距离等于.
应用:如图,在数轴上,动点A从表示的点出发,以1个单位长度/秒的速度沿着数轴的正方向运动.同时,动点B从表示12的点出发,以2个单位长度/秒的速度沿着数轴的负方向运动.
(1)经过多长时间,点A,B之间的距离等于3个单位长度?
(2)求点A,B到原点距离之和的最小值.
19.(8分)[2024年山东泰安中考真题]某超市打算购进一批苹果,现从甲、乙两个供应商供应的苹果中各随机抽取10个,测得它们的直径(单位:),并制作统计图如下:
根据以上信息,解答下列问题:
(1)
统计量供应商 平均数 中位数 众数
甲 80 80 b
乙 m a 76
则____________,____________,____________.
(2)苹果直径的方差越小,苹果的大小越整齐,据此判断,____________供应商供应的苹果大小更为整齐.(填“甲”或“乙”)
(3)超市规定直径(含)以上的苹果为大果,超市打算购进甲供应商的苹果3500个,那么大果约有多少个?
20.(8分)[2024年广西中考真题]如图,已知是的外接圆,.点D,E分别是,的中点,连接并延长至点F,使,连接.
(1)求证:四边形是平行四边形;
(2)求证:与相切;
(3)若,,求的半径.
21.(9分)[2024年北京中考真题]在平面直角坐标系中,函数与的图象交于点.
(1)求k,b的值;
(2)当时,对于x的每一个值,函数的值既大于函数的值,也大于函数的值,直接写出m的取值范围.
22.(9分)[2024年广东中考真题]中国新能源汽车为全球应对气候变化和绿色低碳转型作出了巨大贡献.为满足新能源汽车的充电需求,某小区增设了充电站,如图是矩形PQMN充电站的平面示意图,矩形ABCD是其中一个停车位.经测量,,,,,GH是另一个车位的宽,所有车位的长宽相同,按图示并列划定.
根据以上信息回答下列问题:(结果精确到0.1m,参考数据)
(1)求PQ的长;
(2)该充电站有20个停车位,求PN的长.
23.(11分)[2024年江苏淮安中考真题]二次函数的图像经过点,顶点为P.
(1)______;
(2)当时,
①若顶点P到x轴的距离为10,则______;
②直线m过点且垂直于y轴,顶点P到直线m的距离为h,随着b的增大,h的值如何变化?请描述变化过程,并说明理由;
(3)若二次函数图像交x轴于B、C两点,点B坐标为,且的面积不小于20,求a的取值范围.
24.(12分)[2025届·河南郑州·一模]如图1,在矩形中,,,连接,与重合,将绕点A顺时针方向旋转,连接,.
(1)旋转过程中一定是等腰三角形的三角形有______,的值为______.
(2)如图2,当点E落在对角线上时,求的长.
(3)连接,试探究能否构成以为直角边的,若能,直接写出线段的长;若不能,请说明理由.
参考答案
1.答案:A
解析:因为,所以气温最低的是北京,故选A.
2.答案:B
解析:由题意可知图③是从“四角亭”上方看到的,即为俯视图.
故选B.
3.答案:C
解析:;
故选:C.
4.答案:D
解析:,
,
,
,
.
故选:D.
5.答案:A
解析:,
,
,
,
故选:A.
6.答案:B
解析:第一个三角形的斜边长,
第二个三角形的斜边长
第九个三角形的斜边长
则这海螺图形周长
与最接近的整数是3,
与最接近的整数是13,
故选:B.
7.答案:A
解析:设每头牛值x金,每头羊值y金,牛5头,羊2头,共值10金;牛2头,羊5头,共值8金,,故选:A.
8.答案:D
解析:将三张卡片分别记为A,B,C,
列表如下:
A B C
A
B
C
共有9种等可能的结果,其中两次抽取的卡片,正面相同的结果有3种,
两次抽取的卡片正面相同的概率为.
故选:D.
9.答案:C
解析:∵,,
∴,
∴,
∵,点D是边上的中点,
∴,
∵,
∴,
故选:C.
10.答案:C
解析:为半圆O的直径,,,,由作图知,是的角平分线,,故选:C.
11.答案:D
解析:由题意得,
∴
∵四边形是菱形,
∴,
∴,
∴,
∴,
∴,
在中,,
∴,
即平移距离,
故选:D.
12.答案:C
解析:二次函数解析式为,
二次函数开口向上,且对称轴为
顶点坐标为.
当时,
当时,.
故A、B错误,不符合题意;
当时,,由二次函数对称性可知点和点关于对称轴对称,在对称轴右侧,y随z的增大而增大,所以当时,;
当时,,由二次函数对称性可知可知点和点关于对称轴对称,在对称轴左侧,y随z的增大而减小,所以当时不一定大于0,
故C正确,符合题意;D错误,不符合题意;故选:C.
13.答案:
解析:
,
解得:,
经检验:是原方程的解,
所以,原方程的解为,
故答案为:.
14.答案:3
解析:设该方程的另一个根为,
由题意可得:,
∴,
∴另一个根为,
故答案为:.
15.答案:
解析:作D关于OA的对称点,
作D关于OB的对称得,
连接,交OA、OB于F、G,
此时的周长最小,
最小值为,连、、,
由轴对称的性质可知,,,
,,,,
,,
,
,
故答案为.
16.答案:①②④
解析:,,四边形是矩形;
,
,故①符合题意;
如图,连接,,,与的交点为K,
,
,
,
的面积等于四边形的面积;故②符合题意;
如图,连接,
轴,,
四边形为矩形,
,
当最小,则最小,
设,
,
,
的最小值为2,故③不符合题意;
如图,设平移距离为n,
,
反比例函数为,四边形为矩形,
,,
,,,,
,
,
,
,
,
,故④符合题意;
故答案为:①②④.
17.答案:(1)5
(2)同意;理由见解析
解析:∵是“半和数”,∴.
∵,,
∴.
∴;
(2)同意.
设是一个“半和数”,则.
∴.
∵a,c整数,
∴为整数.
∴任意一个“半和数”都能被3整除.
18.答案:(1)4秒或6秒
(2)3
解析:(1)设运动时间为x秒,则点A表示的数为,点B表示的数为,
根据题意,得,
解得或6.
答:经过4秒或6秒,点A,B之间的距离等于3个单位长度.
(2)由(1)知,点A,B到原点距离之和为.
当时,.
,,即.
当时,.
,,即.
当时,.
,,即.
综上可知,点A,B到原点距离之和的最小值为3.
19.答案:(1)80,,83
(2)甲
(3)1050
解析:(1),
对乙的10个数据进行排序为:75,76,76,76,79,80,81,83,86,88,
所以,中位数为,
通过观察甲的数据可知83出现的次数最多,故众数.
故答案为:80,,83.
(2)
所以,甲的方差比乙的方差小,
故答案为:甲.
(3)(个)
所以,大果约有1050个.
20.答案:(1)证明见解析
(2)证明见解析
(3)10
解析:(1)证明:点D,E分别是,的中点,
,,
又,,
,
,,
,,
四边形是平行四边形;
(2)证明:如图,连接,
,D为中点,
,
过圆心,
,
,
而为半径,
为的切线;
(3)如图,过B作于Q,连接,
,
,
设,则,
,
,
,
,
,
,
,,,
,
,
设半径为r,
,
,
解得:,
的半径为10.
21.答案:(1),
(2)
解析:(1)由题意得将代入得:,
解得:,
将,,代入函数中,
得:,
解得:,
,;
(2),,
两个一次函数的解析式分别为,,
当时,对于x的每一个值,函数的值既大于函数的值,也大于函数的值,
即当时,对于x的每一个值,直线的图像在直线和直线的上方,则画出图象为:
由图象得:当直线与直线平行时符合题意或者当与x轴的夹角大于直线与直线平行时的夹角也符合题意,
当直线与直线平行时,,
当时,对于x的每一个值,直线的图像在直线和直线的上方时,,
m的取值范围为.
22.答案:(1)6.1m
(2)66.7m
解析:(1)四边形PQMN是矩形,
,
在中,,,
,,
四边形ABCD是矩形,
,,
,
,
,
,
,
.
(2)中,,
在中,,
该充电站有20个停车位,
,
四边形ABCD是矩形,
.
23.答案:(1)8
(2)①
②见解析
(3)或且
解析:(1)将点A坐标代入抛物线表达式得:
故答案为:8;
(2)①当时,抛物线的表达式为:
,
则,
即,
解得:,
故答案为:;
②顶点P的纵坐标为:,
则,
令,则或,
函数h的大致图象如下:
从图象看,当或时,h随b的最大而增大,当或时,h随b的增大而减小;
(3)设点C、B的横坐标为m,n,
将点B的坐标代入抛物线得:,
则,
即抛物线的表达式为:,
则,,
则,
则的面积,
即,
则或,
解得:或且.
24.答案:(1),,
(2)的长为或
(3)能,或,理由见解析
解析:(1)∵四边形是矩形,,,
∴,,,
∴,
∵与重合,
∴,,,,
∴将绕点A顺时针方向旋转时,,,
∴,是等腰三角形,
∵旋转,
∴,
又,
∴,
∴,
故答案为:,,;
(2)第一种情况,如图所示,点E在上时,
∴,,,
∴,
在中,,
由(1)可得,,
∴;
第二种情况,如图所示,点E在延长线时,
∴,
在中,,
∵,
∴,即,
∴;
综上所述,的长为或;
(3)能,或,理由如下,
第一种情况,如图所示,,是以为直角边的三角形,
由(1)可得,,,
∴设,,
∵旋转,
∴,,,
∴是等腰三角形,
过点A作于点H,交于点K,
∴,
∵,
∴,
∴,
∴,
∴点K是的中点,
∴,
在中,,
∴,
在中,,,
∴,
∴,
在中,,点K是中点,
∴,
在中,,
∴,
整理得,,
解得,(负值舍去),
∴;
第二种情况,如图所示,,是以为直角边的三角形,
∵与重合,
∴,,,,
∴,是等腰三角形,
∴,
过点A作与点G,
∴,,
∴四边形是矩形,
∴,
∴;
综上所述,能构成以为直角边的,线段的长为或6.
同课章节目录
