【期末押题卷】广东省广州市2024-2025学年六年级下学期数学期末测试押题预测卷二(人教版)(含解析)
文档属性
| 名称 | 【期末押题卷】广东省广州市2024-2025学年六年级下学期数学期末测试押题预测卷二(人教版)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 622.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-06 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
广东省广州市2024-2025学年六年级下学期数学期末押题预测卷
一.选择题(共10小题,满分20分,每小题2分)
1.(2分)(2024 长沙模拟)通常,我们规定海平面的海拔高度为0m,A山的海拔高度是250m,B盆地的海拔高度是﹣150m,A、B两地的海拔高度相距( )米。
A.100 B.﹣100 C.400
2.(2分)(2022 龙里县)直角三角形绕其一条直角边旋转一周可能得到( )
A. B. C.
3.(2分)(2024春 临清市校级期中)从聊城到菏泽,客车要行驶4小时,货车要行驶5小时。客车的速度比货车快( )%。
A.20 B.25 C.80 D.15
4.(2分)(2023 渌口区)把一个底面积是8cm2、高是6cm的圆柱切成4个小圆柱,它的表面积增加( )cm2。
A.24 B.32 C.48 D.64
5.(2分)(2023 吴兴区)一个圆柱和一个圆锥的底面积相等,圆柱的体积是圆锥的。圆柱的高是4厘米,圆锥的高是( )厘米。
A.12 B.36 C.24 D.4
6.(2分)(2024秋 丰台区期末)张阿姨把10000元钱存入银行,存三年定期。按年利率1.95%计算,到期后连本带息可取出多少钱?下面列式正确的是( )
A.10000+10000×1.95%×3
B.(10000+10000×1.95%)×3
C.10000×1.95%×3
D.10000+10000×1.95%
7.(2分)(2024春 嘉祥县期中)小芳家客厅长8m,宽5.6m,画在练习本上,选比例尺( )比较合适。
A.1:100 B.1:10 C.1:1000 D.10:1
8.(2分)(2024 扶沟县)在一个拧紧瓶盖的瓶子里装了一些水,根据图中的数据,可以算出瓶中水的体积占瓶子容积的( )
A. B. C.
9.(2分)学校要建两个大小相同的圆柱形花坛,花坛的直径是2米,要填厚40cm的土,若每立方米的土重约750千克,那么填花坛需要土( )千克。
A.300π B.600π C.1200π D.2400π
10.(2分)(2025春 宝安区期中)在当今时代,芯片堪称各类电子产品的“智慧大脑”,其重要性不言而喻。有一款用于新型智能设备的长方形芯片,它实际长1.5厘米,宽0.9厘米。在技术设计图纸上,这款芯片被绘制为长6分米,宽3.6分米。那么,这张图纸的比例尺是多少呢?( )
A.1:4 B.4:1 C.1:40 D.40:1
二.填空题(共12小题,满分24分,每小题2分)
11.(2分)(2024春 黄石期中)李亮在银行存了10000元压岁钱,利率为2.25%,存满4年后,他能得利息 元,本息一共可以取回 元。
12.(2分)(2023春 蚌山区校级期中)一根长2米,底面直径是4分米的圆柱形木料浮在水面上,如图,小华发现它正好有一半露出水面。
(1)这根木料的体积是 立方分米。
(2)这根木料露出水面部分的面积一共是 平方分米。
13.(2分)(2023 武进区)小明和妈妈乘坐地铁一号线从清凉寺站到环球港站,票价4元。小明刷学生卡,可以享受五折优惠,妈妈用常州地铁APP扫码,可以享受八五折优惠。妈妈乘地铁要支付 元,小明支付的费用比妈妈便宜了。
14.(2分)(2024春 斗门区校级期中)一张底3dm,高5dm的直角三角形纸片,以高为轴旋转一周形成一个 ,它的体积是 dm3。
15.(2分)(2025春 宁乡市期中)16÷20== :5= (小数)= %= 折。
16.(2分)(2023 通辽)如图所示,把一个棱长是12分米的正方体木料削成个最大的圆柱,圆柱的体积是 立方分米;再把该圆柱削成一个最大的圆锥,还要再削去 立方分米。
17.(2分)(2024春 泰兴市期中)一个圆柱高10厘米,把它的高缩短3厘米,表面积就减少94.2平方厘米。这个圆柱原来的底面积是 平方厘米,现在的体积是 立方厘米。
18.(2分)(2022秋 钟山区期末)学校图书室原有图书1400册,今年图书数量增加了12%。把 看作单位“1”,今年图书数量是去年的 %。
19.(2分)(2023 甘谷县)一个圆柱的底面周长是12.56cm,高是3cm,这个圆柱的表面积是 cm2,与它等底等高的圆锥的体积是 cm3。
20.(2分)(2023 巨野县)如果、B都不为零),则A:B= : ,A与B成 比例。
21.(2分)(2024春 商水县期中)判断下面各题中的两种量是否成比例?如果成比例,成什么比例?
(1)买足球的总价一定,买足球的个数与单价。
(2)大米的总质量一定,吃了的和剩下的。
(3)工作时间一定,工作总量与工作效率。
(4)长方体的体积一定,它的底面积与高。
22.(2分)(2022 大兴区)弹簧秤可以用来称物体的质量。悬挂物体的质量不同,弹簧伸长的长度也不同。有一个弹簧秤最多能称6千克重的物体。先观察如表,再填空。
悬挂物体的质量(千克) 1 2 3 ……
弹簧伸长的长度(厘米) 3 6 9 ……
如果悬挂5千克的物体,那么弹簧伸长的长度是 厘米;如果弹簧伸长的长度是7.5厘米,那么悬挂物体的质量是 千克。
三.计算题(共4小题,满分29分)
23.(8分)(2023春 零陵区期中)直接写出得数。
1.25×2.4= 10﹣10%= ×0= =
3.5÷0.2= = 2.4×= 16×0.25=
24.(12分)(2024 平桥区)脱式计算,能简算的要简算。
(1)
(2)
(3)18.67﹣(5.77+4.17)﹣4.23
(4)78×103
25.(6分)(2024 郏县)解方程。
(1)
(2)
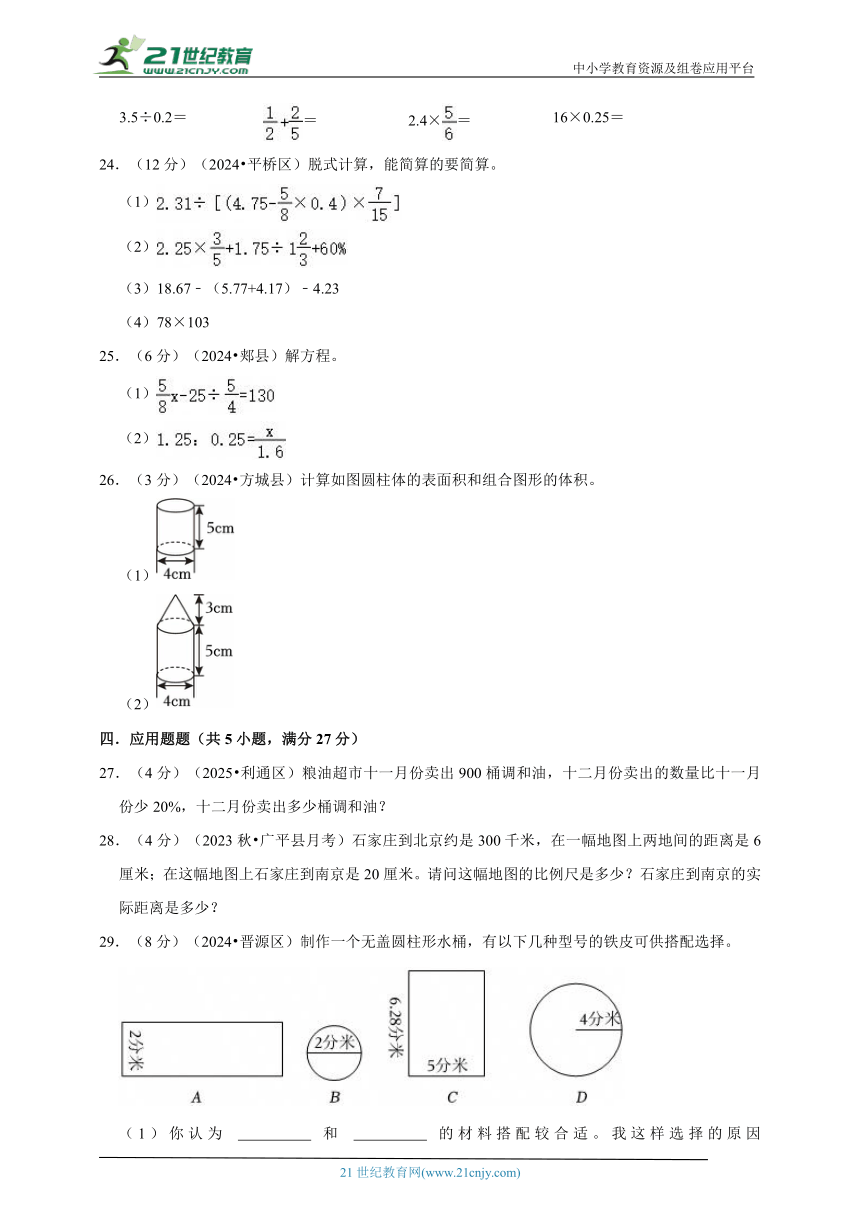
26.(3分)(2024 方城县)计算如图圆柱体的表面积和组合图形的体积。
(1)
(2)
四.应用题题(共5小题,满分27分)
27.(4分)(2025 利通区)粮油超市十一月份卖出900桶调和油,十二月份卖出的数量比十一月份少20%,十二月份卖出多少桶调和油?
28.(4分)(2023秋 广平县月考)石家庄到北京约是300千米,在一幅地图上两地间的距离是6厘米;在这幅地图上石家庄到南京是20厘米。请问这幅地图的比例尺是多少?石家庄到南京的实际距离是多少?
29.(8分)(2024 晋源区)制作一个无盖圆柱形水桶,有以下几种型号的铁皮可供搭配选择。
(1)你认为 和 的材料搭配较合适。我这样选择的原因是: 。
(2)你选择的材料制作水桶的容积是 升。
30.(5分)(2023春 恩平市期中)根据条件求圆柱的表面积。(单位:厘米)
31.(6分)(2024春 汶上县期中)居民小区的健身设施需要定期进行维护和修缮,王伯伯运来一车沙子要用来维护小区的一个沙坑。这些沙子堆成了一个圆锥形,量得底面周长是25.12米,高3米。(π取3.14)
(1)这些沙子的体积是多大?
(2)沙坑长20米、宽12.56米,需要填沙子的厚度是20厘米,这些沙子够用吗?
广东省广州市2024-2025学年六年级下学期数学期末测试押题预测卷
参考答案与试题解析
一.选择题(共10小题,满分20分,每小题2分)
1.(2分)(2024 长沙模拟)通常,我们规定海平面的海拔高度为0m,A山的海拔高度是250m,B盆地的海拔高度是﹣150m,A、B两地的海拔高度相距( )米。
A.100 B.﹣100 C.400
【考点】负数的意义及其应用.
【专题】整数的认识;数据分析观念.
【答案】C
【分析】A、B两地的海拔距离我们可以把它分成两部分,A山的海拔高度到0点的距离为250米,B盆地的海拔高度到0点的距离为150米,两地的距离=A山的海拔高度到0点的距离+B盆地的海拔高度到0点的距离
【解答】解:250+150=400(米)
故答案为:C。
【点评】此题考查正负数在实际生活中的应用,解题关键是理解“正”和“负”的相对性,确定一对具有相反意义的量。
2.(2分)(2022 龙里县)直角三角形绕其一条直角边旋转一周可能得到( )
A. B. C.
【考点】圆锥的特征;将简单图形平移或旋转一定的度数.
【专题】空间观念;几何直观.
【答案】A
【分析】根据“点动成线,线动成面,面动成体”,一个直角三角形绕它的一条直角边旋转一周,可得到一个以旋转轴的直角边为高,另一直角边为底的圆锥。
【解答】解:直角三角形绕其一条直角边旋转一周可能得到。
故选:A。
【点评】此题主要考查学生的空间观念。
3.(2分)(2024春 临清市校级期中)从聊城到菏泽,客车要行驶4小时,货车要行驶5小时。客车的速度比货车快( )%。
A.20 B.25 C.80 D.15
【考点】百分数的实际应用.
【专题】对应法;模型思想.
【答案】B
【分析】把聊城到菏泽的路看作单位“1”,除以相应的行驶时间可得两车的速度,进而求得客车的速度比货车快的百分率。
【解答】解:客车速度:
,
货车速度:
,
客车的速度比货车快:
=
=25%。
答:客车的速度比货车快25%。
故选:B。
【点评】本题考查了百分数的实际应用问题,解答时一定要清楚:求一个数比另一个数多或少百分之几,“是、比、占……”之后的数量为单位“1”,用两个数量之差除以单位“1”表示的数量,最后结果用百分数表示。
4.(2分)(2023 渌口区)把一个底面积是8cm2、高是6cm的圆柱切成4个小圆柱,它的表面积增加( )cm2。
A.24 B.32 C.48 D.64
【考点】圆柱的侧面积和表面积.
【专题】立体图形的认识与计算;几何直观.
【答案】C
【分析】根据题意可知,把这个大圆柱切成4个小圆柱,需要切3次,每切一次就增加两个切面的面积,那么切3次就增加6个切面的面积。
【解答】解:6×8=48(平方厘米)
答:它的表面积增加48cm2。
故选:C。
【点评】解答此题的关键是理解切成后的截面的样子。
5.(2分)(2023 吴兴区)一个圆柱和一个圆锥的底面积相等,圆柱的体积是圆锥的。圆柱的高是4厘米,圆锥的高是( )厘米。
A.12 B.36 C.24 D.4
【考点】圆锥的体积;圆柱的体积.
【专题】立体图形的认识与计算;应用意识.
【答案】B
【分析】根据等底等高的圆柱体积是圆锥体积的3倍,一个圆柱和一个圆锥的底面积相等,圆柱的体积是圆锥的,圆柱的高就是圆锥高的÷3=,圆柱的高是4厘米,圆锥的高是4÷,据此解答。
【解答】解:4÷(÷3)
=4÷
=36(厘米)
答:圆锥的高是36厘米。
故选:B。
【点评】本题考查的是圆柱和圆锥的体积,掌握等底等高的圆柱体积是圆锥体积的3倍是解答关键。
6.(2分)(2024秋 丰台区期末)张阿姨把10000元钱存入银行,存三年定期。按年利率1.95%计算,到期后连本带息可取出多少钱?下面列式正确的是( )
A.10000+10000×1.95%×3
B.(10000+10000×1.95%)×3
C.10000×1.95%×3
D.10000+10000×1.95%
【考点】存款利息与纳税相关问题.
【专题】应用题;应用意识.
【答案】A
【分析】利息=本金×年利率×存期,据此代入数据计算即可求出利息,再加本金即可求出到期后连本带息的钱数。
【解答】解:10000+10000×1.95%×3
=10000+585
=10585(元)
故选:A。
【点评】此题考查学生解答存款利息问题的能力。
7.(2分)(2024春 嘉祥县期中)小芳家客厅长8m,宽5.6m,画在练习本上,选比例尺( )比较合适。
A.1:100 B.1:10 C.1:1000 D.10:1
【考点】比例尺.
【专题】数感;运算能力;应用意识.
【答案】A
【分析】实际距离和比例尺已知,依据“图上距离=实际距离×比例尺”,即可求出小芳家客厅的长和宽的图上距离,再与练习本的实际长度比较即可选出合适的答案。
【解答】解:因为8米=800厘米,5.6米=560厘米
A、800×=8(厘米),560×=5.6(厘米),画在练习本比较合适;
B、800×=80(厘米),560×=56(厘米),画在练习本上,尺寸太大,不符合实际情况,故不合适;
C、800×=0.8(厘米),560×=0.56(厘米),画在练习本上尺寸太小,故不合适;
D、800×=8000(厘米),560×=5600(厘米),画在练习本上尺寸太大,故不合适。
故选:A。
【点评】此题主要考查图上距离、实际距离和比例尺的关系,解答时要注意结合实际情况。
8.(2分)(2024 扶沟县)在一个拧紧瓶盖的瓶子里装了一些水,根据图中的数据,可以算出瓶中水的体积占瓶子容积的( )
A. B. C.
【考点】圆柱的体积.
【专题】应用意识.
【答案】C
【分析】根据体积的意义可知,瓶子无论正放,还是倒放,瓶子里水的体积不变。瓶子的容积相当于以瓶子的底面为底面,高为(16﹣14+10)厘米的圆柱的容积,因为底面积不变,所以高和体积成正比例,正放时瓶子里水的高占(16﹣14+10)厘米的几分之几,也就是瓶中水的体积占瓶子容积的几分之几。据此解答即可。
【解答】解:10÷(16﹣14+10)
=10÷12
=
答:瓶中水的体积占瓶子容积的。
故选:C。
【点评】此题主要考查圆柱的体积(容积)公式的灵活运用,关键是熟记公式。
9.(2分)学校要建两个大小相同的圆柱形花坛,花坛的直径是2米,要填厚40cm的土,若每立方米的土重约750千克,那么填花坛需要土( )千克。
A.300π B.600π C.1200π D.2400π
【考点】圆柱的体积.
【专题】空间观念;应用意识.
【答案】B
【分析】根据圆柱的体积公式:V=πr2h,把数据代入公式求出填两个花坛需要土的体积,然后用土的体积乘每立方米土的质量即可。
【解答】解:40厘米=0.4米
3.14×(2÷2)2×0.4×2×750
=3.14×1×0.4×2×750
=2.512×750
=1884(千克)
答:填花坛需要土1884千克。
故选:B。
【点评】此题主要考查圆柱体积公式的灵活运用,关键是熟记公式。
10.(2分)(2025春 宝安区期中)在当今时代,芯片堪称各类电子产品的“智慧大脑”,其重要性不言而喻。有一款用于新型智能设备的长方形芯片,它实际长1.5厘米,宽0.9厘米。在技术设计图纸上,这款芯片被绘制为长6分米,宽3.6分米。那么,这张图纸的比例尺是多少呢?( )
A.1:4 B.4:1 C.1:40 D.40:1
【考点】比例尺.
【专题】推理能力;应用意识.
【答案】D
【分析】比例尺=图上距离:实际距离,根据题意可直接求得比例尺。
【解答】解:6分米:1.5厘米
=60厘米:1.5厘米
=60:1.5
=40:1
答:这张图纸的比例尺是40:1。
故选:D。
【点评】考查了比例尺的概念,掌握比例尺的计算方法,注意在求比的过程中,单位要统一。
二.填空题(共12小题,满分24分,每小题2分)
11.(2分)(2024春 黄石期中)李亮在银行存了10000元压岁钱,利率为2.25%,存满4年后,他能得利息 900 元,本息一共可以取回 10900 元。
【考点】存款利息与纳税相关问题.
【专题】应用题;应用意识.
【答案】900;10900。
【分析】先利用公式:利息=本金×利率×存期,算出利息是多少,再加本金即可。
【解答】解:10000×2.25%×4
=10000×2.25%×4
=225×4
=900(元)
10000+900=10900(元)
答:他能得利息900元,本息一共可以取回10900元。
故答案为:900;10900。
【点评】主要考查利息的计算公式:利息=本金×利率×存期。
12.(2分)(2023春 蚌山区校级期中)一根长2米,底面直径是4分米的圆柱形木料浮在水面上,如图,小华发现它正好有一半露出水面。
(1)这根木料的体积是 251.2 立方分米。
(2)这根木料露出水面部分的面积一共是 138.16 平方分米。
【考点】圆柱的侧面积、表面积和体积.
【专题】综合填空题;应用意识.
【答案】(1)251.2;(2)138.16。
【分析】(1)根据圆柱体积=底面积×高,列式计算即可;
(2)露出水面部分包括侧面积的一半和两个底面积的一半,两个底面积的一半可以拼成一个底面积,露出水面部分的面积=侧面积÷2+底面积,圆柱侧面积=底面周长×高,据此列式计算。
【解答】解:(1)2米=20分米,4÷2=2(分米)
3.14×2×2×20=251.2(立方分米)
答:体积是251.2立方分米。
(2)3.14×4×20÷2+3.14×2×2
=125.6+12.56
=138.16(平方分米)
答:这根木料露出水面部分的面积一共是138.16平方分米。
故答案为:(1)251.2;(2)138.16。
【点评】本题考查的是圆柱的侧面积、体积公式的应用。
13.(2分)(2023 武进区)小明和妈妈乘坐地铁一号线从清凉寺站到环球港站,票价4元。小明刷学生卡,可以享受五折优惠,妈妈用常州地铁APP扫码,可以享受八五折优惠。妈妈乘地铁要支付 3.4 元,小明支付的费用比妈妈便宜了。
【考点】百分数的实际应用;折扣.
【专题】应用题;应用意识.
【答案】3.4;。
【分析】五折是50%,八五折就是85%,用票价乘85%就是妈妈乘地铁需要支付的钱数;用4乘50%求出小明需要付的钱数,先求出小明比妈妈少付的钱数,再除以妈妈付的钱数即可。
【解答】解:4×85%=3.4(元)
4×50%=2(元)
(3.4﹣2)÷3.4
=2÷2.4
=
答:妈妈乘地铁要支付3.4元,小明支付的费用比妈妈便宜了。
故答案为:3.4;。
【点评】解答此题的关键是找准单位“1”的量。
14.(2分)(2024春 斗门区校级期中)一张底3dm,高5dm的直角三角形纸片,以高为轴旋转一周形成一个 圆锥 ,它的体积是 47.1 dm3。
【考点】圆锥的体积.
【专题】应用题;应用意识.
【答案】圆锥;47.1。
【分析】根据题意可知,这个直角三角形旋转一周得到的是圆锥;其中直角三角形的底是圆锥的底面半径,高是圆锥的高;根据圆锥的体积公式:体积=底面积×高×,代入数据,即可解答。
【解答】解:旋转一周形成一个圆锥。
3.14×32×5×
=3.14×3×5
=3.14×15
=47.1(dm3)
故答案为:圆锥;47.1。
【点评】此题主要考查圆锥体积公式的灵活应用,关键是熟记公式。
15.(2分)(2025春 宁乡市期中)16÷20== 4 :5= 0.8 (小数)= 80 %= 八 折。
【考点】比与分数、除法的关系;小数、分数和百分数之间的关系及其转化;折扣.
【专题】数感.
【答案】10;4;0.8;80;八。
【分析】根据分数与除法的关系16÷20=,再根据分数的基本性质,的分子、分母都除以2就是;根据比与除法的关系16÷20=16:20,再根据比的性质,比的前、后项都除以4就是4:5;16÷20=0.8;把0.8的小数点向右移动两位添上百分号就是80%;根据折扣的意义80%就是八折。
【解答】解:16÷20==4:5=0.8=80%=八折
故答案为:10;4;0.8;80;八。
【点评】此题主要是考查小数、分数、除法、比、百分数、折扣之间的关系及转化。利用它们之间的关系和性质进行转化即可。
16.(2分)(2023 通辽)如图所示,把一个棱长是12分米的正方体木料削成个最大的圆柱,圆柱的体积是 1356.48 立方分米;再把该圆柱削成一个最大的圆锥,还要再削去 904.32 立方分米。
【考点】圆柱的侧面积、表面积和体积;圆锥的体积.
【专题】立体图形的认识与计算.
【答案】1356.48,904.32。
【分析】根据题意,削成一个最大的圆柱体或最大的圆锥体的底面直径为12分米,高为12分米,可根据圆柱或圆锥的体积公式进行计算即可得到答案。
【解答】解:底面半径为:12÷2=6(分米)
圆柱的体积为:
3.14×62×12
=113.04×12
=1356.48(立方分米)
圆锥的体积为:×3.14×62×12
=3.14×36×4
=452.16(立方分米)
1356.48﹣452.16=904.32(立方分米)
答:圆柱的体积是1356.48立方分米,再将圆柱削成一个最大的圆锥,还要再削去904.32立方分米。
故答案为:1356.48,904.32。
【点评】解答此题的关键是确定削成的最大的圆柱体或圆锥体的底面直径和高,然后再根据圆柱和圆锥的体积公式进行计算即可。
17.(2分)(2024春 泰兴市期中)一个圆柱高10厘米,把它的高缩短3厘米,表面积就减少94.2平方厘米。这个圆柱原来的底面积是 78.5 平方厘米,现在的体积是 549.5 立方厘米。
【考点】圆柱的侧面积、表面积和体积.
【专题】应用意识.
【答案】78.5,549.5。
【分析】根据题意可知,把这个圆柱的高缩短3厘米,表面积减少94.2平方厘米,表面积减少的是高为3厘米的圆柱的侧面积,据此可以求出圆柱的底面半径,再根据圆的面积公式:S=πr2,圆柱的体积公式:V=Sh,把数据代入公式解答。
【解答】解:94.2÷3÷3.14÷2
=31.4÷3.14÷2
=5(厘米)
3.14×52
=3.14×25
=78.5(平方厘米)
78.5×(10﹣3)
=78.5×7
=549.5(立方厘米)
答:这个圆柱原来的面积是78.5平方厘米,现在的体积是549.5立方厘米。
故答案为:78.5,549.5。
【点评】此题主要考查圆柱的侧面积公式、体积公式的灵活运用,关键是熟记公式。
18.(2分)(2022秋 钟山区期末)学校图书室原有图书1400册,今年图书数量增加了12%。把 原有图书数量 看作单位“1”,今年图书数量是去年的 112 %。
【考点】百分数的实际应用;单位“1”的认识及确定.
【答案】原有图书数量,112。
【分析】今年图书数量增加了12%也就是今年图书增加的数量相当于原有图书量的12%,是将原有图书数量看作单位“1”,今年图书数量是去年的1+12%;据此解答。
【解答】解:1+12%=112%
学校图书室原有图书1400册,今年图书数量增加了12%。把原有图书数量看作单位“1”,今年图书数量是去年的112%。
故答案为:原有图书数量,112。
【点评】单位“1”怎么找的口诀:“是”“比”“占”“相当于”,后面就是单位“1”;“的”字前面是单位“1”。
19.(2分)(2023 甘谷县)一个圆柱的底面周长是12.56cm,高是3cm,这个圆柱的表面积是 62.8 cm2,与它等底等高的圆锥的体积是 12.56 cm3。
【考点】圆柱的侧面积、表面积和体积;圆锥的体积.
【专题】立体图形的认识与计算;空间观念;运算能力.
【答案】见试题解答内容
【分析】(1)圆柱的底面是一个圆,圆的周长公式:C=2πr,把底面周长12.56cm代入公式求出它的底面半径,然后再根据圆的面积公式:S=πr2,进行计算求出底面积;再根据圆柱的侧面积公式:S=Ch=2πrh,进行计算求出侧面积;根据圆柱的表面积=侧面积+2个底面积,求出表面积;
(2)根据圆柱的体积V=Sh=πr2h进行计算求出体积;再根据等底等高的圆锥的体积是圆柱的体积的,用圆柱的体积乘求出圆锥的体积。
【解答】解:(1)圆柱的底面半径为:12.56÷3.14÷2=2(cm)
底面积:22×3.14
=4×3.14
=12.56(cm2)
侧面积:2×3.14×2×3
=6.28×2×3
=37.68(cm2)
表面积:12.56×2+37.68
=25.12+37.68
=62.8(cm2)
(2)3.14×22×3×
=3.14×4
=12.56(cm3)
答:这个圆柱的表面积是62.8cm2,与它等底等高的圆锥的体积是12.56cm3。
故答案为:62.8;12.56。
【点评】此题主要考查圆柱的底面积、底面周长、侧面积和体积的计算,直接把数据代入它们的公式解答。
20.(2分)(2023 巨野县)如果、B都不为零),则A:B= 4 : 3 ,A与B成 正 比例。
【考点】比例的意义和基本性质.
【专题】运算能力;推理能力.
【答案】4,3;正。
【分析】先根据比例的基本性质求出A与B的比,然后求出比值,再根据比值确定A与B成什么比例。
【解答】解:由A×=B×得:
A:B
=:
=(×6):(×6)
=4:3
=
A与B的比值一定,A与B成正比例。
故答案为:4,3;正。
【点评】解答本题需熟练掌握比例的基本性质,明确化简比的方法,准确辨识两种相关联的量乘说明比例关系。
21.(2分)(2024春 商水县期中)判断下面各题中的两种量是否成比例?如果成比例,成什么比例?
(1)买足球的总价一定,买足球的个数与单价。 成反比例
(2)大米的总质量一定,吃了的和剩下的。 不成比例
(3)工作时间一定,工作总量与工作效率。 成正比例
(4)长方体的体积一定,它的底面积与高。 成反比例
【考点】辨识成正比例的量与成反比例的量.
【专题】推理能力.
【答案】(1)成反比例;(2)不成比例;(3)成正比例;(4)成反比例。
【分析】判断两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例;如果是其它的量一定或乘积、比值不一定,就不成比例。
【解答】解:(1)足球的个数×单价=足球的总价(一定);已知总价一定,也就是数量与单价的乘积一定,所以买足球的个数与单价成反比例。
(2)吃了的质量+吃剩的质量=大米的总质量(一定),是和一定,所以大米的总质量一定,吃了的质量和吃剩的质量不成比例;
(3)工作总量÷工作时间=工作效率(一定),是对应的“比值”一定,所以工作时间与工作总量成正比例;
(4)长方体的体积(一定)=它的底面积×高,它们的乘积一定,所以它的底面积与高成反比例。
故答案为:成反比例;不成比例;成正比例;成反比例。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
22.(2分)(2022 大兴区)弹簧秤可以用来称物体的质量。悬挂物体的质量不同,弹簧伸长的长度也不同。有一个弹簧秤最多能称6千克重的物体。先观察如表,再填空。
悬挂物体的质量(千克) 1 2 3 ……
弹簧伸长的长度(厘米) 3 6 9 ……
如果悬挂5千克的物体,那么弹簧伸长的长度是 15 厘米;如果弹簧伸长的长度是7.5厘米,那么悬挂物体的质量是 2.5 千克。
【考点】正、反比例应用题;数表中的规律.
【答案】15,2.5。
【分析】观察所给出的表知道,物体的重量与弹簧伸出的长度的比是1:3,由此判断物体的重量与弹簧伸长的长度成正比例,设出未知数,列出比例解答即可。
【解答】解:(1)设弹簧伸长的长度是x厘米
5:x=1:3
x=5×3
x=15
(2)设悬挂的物体重x千克
x:7.5=1:3
3x=7.5×1
x=2.5
答:弹簧伸长的长度是15厘米;悬挂的物体重2.5千克。
故答案为:15,2.5。
【点评】解答此题的关键是根据表中给出的物体的重量与弹簧伸出的长度的比值一定,得出物体的重量与弹簧伸出的长度成正比例.
三.计算题(共4小题,满分29分)
23.(8分)(2023春 零陵区期中)直接写出得数。
1.25×2.4= 10﹣10%= ×0= =
3.5÷0.2= = 2.4×= 16×0.25=
【考点】小数乘法;小数除法;分数乘法;分数除法;百分数的加减乘除运算.
【专题】运算能力.
【答案】3;9.9;0;;17.5;;2;4。
【分析】根据百分数减法、小数乘法、小数除法、分数乘法、分数加法、分数除法的计算方法直接写出得数即可。
【解答】解:
1.25×2.4=3 10﹣10%=9.9 ×0=0 =
3.5÷0.2=17.5 = 2.4×=2 16×0.25=4
【点评】本题主要考查了百分数减法、小数乘法、小数除法、分数乘法、分数加法、分数除法的运算,属于基本的计算,在平时注意积累经验,逐步提高运算的速度和准确性。
24.(12分)(2024 平桥区)脱式计算,能简算的要简算。
(1)
(2)
(3)18.67﹣(5.77+4.17)﹣4.23
(4)78×103
【考点】运算定律与简便运算;分数的四则混合运算.
【专题】运算能力.
【答案】(1)1.1;
(2)3;
(3)4.5;
(4)8034。
【分析】(1)先算小括号里面的乘法,再算小括号里面的减法,再算中括号里面的乘法,最后算中括号外面的除法;
(2)(4)根据乘法分配律进行计算;
(3)根据减法的性质进行计算。
【解答】解:(1)
=2.31÷[(4.75﹣0.25)×]
=2.31÷[4.5×]
=2.31÷2.1
=1.1
(2)
=2.25×0.6+1.75×0.6+0.6
=(2.25+1.75+1)×0.6
=5×0.6
=3
(3)18.67﹣(5.77+4.17)﹣4.23
=18.67﹣5.77﹣4.17﹣4.23
=(18.67﹣4.17)﹣(5.77+4.23)
=14.5﹣10
=4.5
(4)78×103
=78×(100+3)
=78×100+78×3
=7800+234
=8034
【点评】考查了运算定律与简便运算,四则混合运算。注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
25.(6分)(2024 郏县)解方程。
(1)
(2)
【考点】分数方程求解;解比例.
【专题】计算题;运算能力.
【答案】(1)x=240;(2)x=8。
【分析】(1),根据等式的性质1和2,两边同时+的商,再同时乘即可;
(2),根据比例的基本性质,先写成0.25x=1.25×1.6的形式,两边同时÷0.25即可。
【解答】解:(1)
x=240
(2)
0.25x=1.25×1.6
0.25x=2
0.25x÷0.25=2÷0.25
x=8
【点评】熟练掌握等式和比例的基本性质是解答本题的关键。
26.(3分)(2024 方城县)计算如图圆柱体的表面积和组合图形的体积。
(1)
(2)
【考点】圆柱的侧面积、表面积和体积;圆锥的体积.
【专题】立体图形的认识与计算;几何直观.
【答案】(1)87.92平方厘米;(2)75.36立方厘米。
【分析】(1)圆柱的表面积=侧面积+两个底面积,用字母表示:S表=2πr2+2πrh;
(2)利用圆柱的体积公式:V=πr2h,求出圆柱的体积;再利用圆锥的体积公式:V=πr2h,求出圆锥的体积,再相加即可。
【解答】解:(1)3.14×4×5+3.14×(4÷2)2×2
=3.14×20+3.14×8
=62.8+25.12
=87.92(平方厘米)
(2)3.14×(4÷2)2×5+×3.14×(4÷2)2×3
=3.14×20+3.14×4
=62.8+12.56
=75.36(立方厘米)
【点评】本题考查了圆柱体的表面积公式及体积公式及圆锥体体积公式的应用。
四.应用题题(共5小题,满分27分)
27.(4分)(2025 利通区)粮油超市十一月份卖出900桶调和油,十二月份卖出的数量比十一月份少20%,十二月份卖出多少桶调和油?
【考点】百分数的实际应用.
【专题】对应法;应用意识.
【答案】720桶。
【分析】读题可知:把十一月份卖出的900桶调和油看作单位“1”,十二月份卖出的调和油比少20%,据此列乘法算式求出它的(1﹣20%)是多少得解。
【解答】解:900×(1﹣20%)
=900×80%
=720(桶)
答:十二月份卖出720桶调和油。
【点评】本题考查了百分数的实际应用问题,解答本题时一定要清楚:单位“1”已知,用乘法作答;单位“1”未知,用除法解答。
28.(4分)(2023秋 广平县月考)石家庄到北京约是300千米,在一幅地图上两地间的距离是6厘米;在这幅地图上石家庄到南京是20厘米。请问这幅地图的比例尺是多少?石家庄到南京的实际距离是多少?
【考点】比例尺.
【专题】比和比例;应用意识.
【答案】;1000千米。
【分析】这幅地图的比例尺=图上距离:实际距离;石家庄到南京的实际距离=图上距离÷比例尺;据此解答。
【解答】解:300千米=30000000厘米
6:30000000=1:5000000
20÷÷100000
=100000000÷100000
=1000(千米)
答:这幅地图的比例尺是 ;石家庄到南京的实际距离是1000千米。
【点评】本题考查比例尺的认识以及应用,掌握应用比例尺求图上距离或实际距离的方法是解题的关键。
29.(8分)(2024 晋源区)制作一个无盖圆柱形水桶,有以下几种型号的铁皮可供搭配选择。
(1)你认为 B 和 C 的材料搭配较合适。我这样选择的原因是: 图C上下拼接后作为圆柱侧面,其底面圆半径是1分米,正好和图B圆半径匹配 。
(2)你选择的材料制作水桶的容积是 15.7 升。
【考点】圆柱的侧面积、表面积和体积.
【专题】综合填空题;应用意识.
【答案】(1)B,C,图C上下拼接后作为圆柱侧面,其底面圆半径是1分米,正好和图B圆半径匹配;(2)15.7。
【分析】(1)图A、C上下或左右拼接后作为圆柱侧面,根据圆柱展开后底面圆周长为长方形的长或宽验证数据是否匹配即可;
(2)通过(1)的选择后匹配的圆柱计算圆柱的体积,根据圆柱的体积计算公式:V=πr2h即可计算。
【解答】解:(1)图A仅知道一条长方形的宽为2分米,上下拼接作为圆柱的侧面,则2分米作为圆柱底面圆周长可知:
2÷3.14÷2≈0.03(分米),即底面圆半径约为0.03分米,图B和图D圆的半径不能和其拼成圆柱。
图B知道长方形的长和宽,上下拼接作为圆柱的侧面,则6.28分米作为圆柱底面圆周长可知:
6.28÷3.14÷2=1(分米),即底面圆半径为1分米,图B圆的半径能和其拼成圆柱。
图B知道长方形的长和宽,上下拼接作为圆柱的侧面,则5分米作为圆柱底面圆周长可知:
5÷3.14÷2≈0.80(分米),即底面圆半径约为0.03分米,图B和图D圆的半径不能和其拼成圆柱。
综上,只有C的长6.28分米作为圆柱底面圆周长时,B可以和C拼成一个圆柱。
答:我认为B和C的材料搭配较合适。我这样选择的原因是:图C上下拼接后作为圆柱侧面,其底面圆半径是1分米,正好和图B圆半径匹配。
(2)3.14×(2÷2)2×5
=3.14×5
=15.7(立方分米)
15.7立方分米=15.7升
答:水桶的容积是15.7升。
故答案为:(1)B,C,图C上下拼接后作为圆柱侧面,其底面圆半径是1分米,正好和图B圆半径匹配;(2)15.7。
【点评】本题考查了图形的拼接以及圆柱体积的计算。
30.(5分)(2023春 恩平市期中)根据条件求圆柱的表面积。(单位:厘米)
【考点】圆柱的侧面积、表面积和体积.
【专题】立体图形的认识与计算;应用意识.
【答案】351.68平方厘米。
【分析】用底面直径除以2求出圆柱底面半径,圆柱的表面积=2πr2+2πrh,代入数据计算即可解答。
【解答】解:8÷2=4(厘米)
3.14×42×2+3.14×8×10
=3.14×16×2+25.12×10
=50.24×2+251.2
=100.48+251.2
=351.68(平方厘米)
答:这个圆柱的表面积是351.68平方厘米。
【点评】此题考查圆柱表面积的计算。掌握圆柱表面积的计算公式是解答的关键。
31.(6分)(2024春 汶上县期中)居民小区的健身设施需要定期进行维护和修缮,王伯伯运来一车沙子要用来维护小区的一个沙坑。这些沙子堆成了一个圆锥形,量得底面周长是25.12米,高3米。(π取3.14)
(1)这些沙子的体积是多大?
(2)沙坑长20米、宽12.56米,需要填沙子的厚度是20厘米,这些沙子够用吗?
【考点】关于圆锥的应用题;长方体和正方体的体积.
【专题】应用意识.
【答案】(1)50.24立方米;
(2)够。
【分析】(1)根据圆锥的体积公式:V=πr2h,把数据代入公式解答。
(2)根据长方体的体积公式:V=abh,把数据代入公式求出需要沙的体积,然后与这堆沙的体积进行比较即可。
【解答】解:(1)×3.14×(25.12÷3.14÷2)2×3
=×3.14×16×3
=50.24(立方米)
答:这些沙的体积是50.24立方米。
(2)20厘米=0.2米
20×12.56×0.2
=251.2×0.2
=50.24(立方米)
50.24=50.24
答:这些沙够。
【点评】此题主要考查圆锥的体积公式、长方体的体积公式的灵活运用,关键是熟记公式。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
广东省广州市2024-2025学年六年级下学期数学期末押题预测卷
一.选择题(共10小题,满分20分,每小题2分)
1.(2分)(2024 长沙模拟)通常,我们规定海平面的海拔高度为0m,A山的海拔高度是250m,B盆地的海拔高度是﹣150m,A、B两地的海拔高度相距( )米。
A.100 B.﹣100 C.400
2.(2分)(2022 龙里县)直角三角形绕其一条直角边旋转一周可能得到( )
A. B. C.
3.(2分)(2024春 临清市校级期中)从聊城到菏泽,客车要行驶4小时,货车要行驶5小时。客车的速度比货车快( )%。
A.20 B.25 C.80 D.15
4.(2分)(2023 渌口区)把一个底面积是8cm2、高是6cm的圆柱切成4个小圆柱,它的表面积增加( )cm2。
A.24 B.32 C.48 D.64
5.(2分)(2023 吴兴区)一个圆柱和一个圆锥的底面积相等,圆柱的体积是圆锥的。圆柱的高是4厘米,圆锥的高是( )厘米。
A.12 B.36 C.24 D.4
6.(2分)(2024秋 丰台区期末)张阿姨把10000元钱存入银行,存三年定期。按年利率1.95%计算,到期后连本带息可取出多少钱?下面列式正确的是( )
A.10000+10000×1.95%×3
B.(10000+10000×1.95%)×3
C.10000×1.95%×3
D.10000+10000×1.95%
7.(2分)(2024春 嘉祥县期中)小芳家客厅长8m,宽5.6m,画在练习本上,选比例尺( )比较合适。
A.1:100 B.1:10 C.1:1000 D.10:1
8.(2分)(2024 扶沟县)在一个拧紧瓶盖的瓶子里装了一些水,根据图中的数据,可以算出瓶中水的体积占瓶子容积的( )
A. B. C.
9.(2分)学校要建两个大小相同的圆柱形花坛,花坛的直径是2米,要填厚40cm的土,若每立方米的土重约750千克,那么填花坛需要土( )千克。
A.300π B.600π C.1200π D.2400π
10.(2分)(2025春 宝安区期中)在当今时代,芯片堪称各类电子产品的“智慧大脑”,其重要性不言而喻。有一款用于新型智能设备的长方形芯片,它实际长1.5厘米,宽0.9厘米。在技术设计图纸上,这款芯片被绘制为长6分米,宽3.6分米。那么,这张图纸的比例尺是多少呢?( )
A.1:4 B.4:1 C.1:40 D.40:1
二.填空题(共12小题,满分24分,每小题2分)
11.(2分)(2024春 黄石期中)李亮在银行存了10000元压岁钱,利率为2.25%,存满4年后,他能得利息 元,本息一共可以取回 元。
12.(2分)(2023春 蚌山区校级期中)一根长2米,底面直径是4分米的圆柱形木料浮在水面上,如图,小华发现它正好有一半露出水面。
(1)这根木料的体积是 立方分米。
(2)这根木料露出水面部分的面积一共是 平方分米。
13.(2分)(2023 武进区)小明和妈妈乘坐地铁一号线从清凉寺站到环球港站,票价4元。小明刷学生卡,可以享受五折优惠,妈妈用常州地铁APP扫码,可以享受八五折优惠。妈妈乘地铁要支付 元,小明支付的费用比妈妈便宜了。
14.(2分)(2024春 斗门区校级期中)一张底3dm,高5dm的直角三角形纸片,以高为轴旋转一周形成一个 ,它的体积是 dm3。
15.(2分)(2025春 宁乡市期中)16÷20== :5= (小数)= %= 折。
16.(2分)(2023 通辽)如图所示,把一个棱长是12分米的正方体木料削成个最大的圆柱,圆柱的体积是 立方分米;再把该圆柱削成一个最大的圆锥,还要再削去 立方分米。
17.(2分)(2024春 泰兴市期中)一个圆柱高10厘米,把它的高缩短3厘米,表面积就减少94.2平方厘米。这个圆柱原来的底面积是 平方厘米,现在的体积是 立方厘米。
18.(2分)(2022秋 钟山区期末)学校图书室原有图书1400册,今年图书数量增加了12%。把 看作单位“1”,今年图书数量是去年的 %。
19.(2分)(2023 甘谷县)一个圆柱的底面周长是12.56cm,高是3cm,这个圆柱的表面积是 cm2,与它等底等高的圆锥的体积是 cm3。
20.(2分)(2023 巨野县)如果、B都不为零),则A:B= : ,A与B成 比例。
21.(2分)(2024春 商水县期中)判断下面各题中的两种量是否成比例?如果成比例,成什么比例?
(1)买足球的总价一定,买足球的个数与单价。
(2)大米的总质量一定,吃了的和剩下的。
(3)工作时间一定,工作总量与工作效率。
(4)长方体的体积一定,它的底面积与高。
22.(2分)(2022 大兴区)弹簧秤可以用来称物体的质量。悬挂物体的质量不同,弹簧伸长的长度也不同。有一个弹簧秤最多能称6千克重的物体。先观察如表,再填空。
悬挂物体的质量(千克) 1 2 3 ……
弹簧伸长的长度(厘米) 3 6 9 ……
如果悬挂5千克的物体,那么弹簧伸长的长度是 厘米;如果弹簧伸长的长度是7.5厘米,那么悬挂物体的质量是 千克。
三.计算题(共4小题,满分29分)
23.(8分)(2023春 零陵区期中)直接写出得数。
1.25×2.4= 10﹣10%= ×0= =
3.5÷0.2= = 2.4×= 16×0.25=
24.(12分)(2024 平桥区)脱式计算,能简算的要简算。
(1)
(2)
(3)18.67﹣(5.77+4.17)﹣4.23
(4)78×103
25.(6分)(2024 郏县)解方程。
(1)
(2)
26.(3分)(2024 方城县)计算如图圆柱体的表面积和组合图形的体积。
(1)
(2)
四.应用题题(共5小题,满分27分)
27.(4分)(2025 利通区)粮油超市十一月份卖出900桶调和油,十二月份卖出的数量比十一月份少20%,十二月份卖出多少桶调和油?
28.(4分)(2023秋 广平县月考)石家庄到北京约是300千米,在一幅地图上两地间的距离是6厘米;在这幅地图上石家庄到南京是20厘米。请问这幅地图的比例尺是多少?石家庄到南京的实际距离是多少?
29.(8分)(2024 晋源区)制作一个无盖圆柱形水桶,有以下几种型号的铁皮可供搭配选择。
(1)你认为 和 的材料搭配较合适。我这样选择的原因是: 。
(2)你选择的材料制作水桶的容积是 升。
30.(5分)(2023春 恩平市期中)根据条件求圆柱的表面积。(单位:厘米)
31.(6分)(2024春 汶上县期中)居民小区的健身设施需要定期进行维护和修缮,王伯伯运来一车沙子要用来维护小区的一个沙坑。这些沙子堆成了一个圆锥形,量得底面周长是25.12米,高3米。(π取3.14)
(1)这些沙子的体积是多大?
(2)沙坑长20米、宽12.56米,需要填沙子的厚度是20厘米,这些沙子够用吗?
广东省广州市2024-2025学年六年级下学期数学期末测试押题预测卷
参考答案与试题解析
一.选择题(共10小题,满分20分,每小题2分)
1.(2分)(2024 长沙模拟)通常,我们规定海平面的海拔高度为0m,A山的海拔高度是250m,B盆地的海拔高度是﹣150m,A、B两地的海拔高度相距( )米。
A.100 B.﹣100 C.400
【考点】负数的意义及其应用.
【专题】整数的认识;数据分析观念.
【答案】C
【分析】A、B两地的海拔距离我们可以把它分成两部分,A山的海拔高度到0点的距离为250米,B盆地的海拔高度到0点的距离为150米,两地的距离=A山的海拔高度到0点的距离+B盆地的海拔高度到0点的距离
【解答】解:250+150=400(米)
故答案为:C。
【点评】此题考查正负数在实际生活中的应用,解题关键是理解“正”和“负”的相对性,确定一对具有相反意义的量。
2.(2分)(2022 龙里县)直角三角形绕其一条直角边旋转一周可能得到( )
A. B. C.
【考点】圆锥的特征;将简单图形平移或旋转一定的度数.
【专题】空间观念;几何直观.
【答案】A
【分析】根据“点动成线,线动成面,面动成体”,一个直角三角形绕它的一条直角边旋转一周,可得到一个以旋转轴的直角边为高,另一直角边为底的圆锥。
【解答】解:直角三角形绕其一条直角边旋转一周可能得到。
故选:A。
【点评】此题主要考查学生的空间观念。
3.(2分)(2024春 临清市校级期中)从聊城到菏泽,客车要行驶4小时,货车要行驶5小时。客车的速度比货车快( )%。
A.20 B.25 C.80 D.15
【考点】百分数的实际应用.
【专题】对应法;模型思想.
【答案】B
【分析】把聊城到菏泽的路看作单位“1”,除以相应的行驶时间可得两车的速度,进而求得客车的速度比货车快的百分率。
【解答】解:客车速度:
,
货车速度:
,
客车的速度比货车快:
=
=25%。
答:客车的速度比货车快25%。
故选:B。
【点评】本题考查了百分数的实际应用问题,解答时一定要清楚:求一个数比另一个数多或少百分之几,“是、比、占……”之后的数量为单位“1”,用两个数量之差除以单位“1”表示的数量,最后结果用百分数表示。
4.(2分)(2023 渌口区)把一个底面积是8cm2、高是6cm的圆柱切成4个小圆柱,它的表面积增加( )cm2。
A.24 B.32 C.48 D.64
【考点】圆柱的侧面积和表面积.
【专题】立体图形的认识与计算;几何直观.
【答案】C
【分析】根据题意可知,把这个大圆柱切成4个小圆柱,需要切3次,每切一次就增加两个切面的面积,那么切3次就增加6个切面的面积。
【解答】解:6×8=48(平方厘米)
答:它的表面积增加48cm2。
故选:C。
【点评】解答此题的关键是理解切成后的截面的样子。
5.(2分)(2023 吴兴区)一个圆柱和一个圆锥的底面积相等,圆柱的体积是圆锥的。圆柱的高是4厘米,圆锥的高是( )厘米。
A.12 B.36 C.24 D.4
【考点】圆锥的体积;圆柱的体积.
【专题】立体图形的认识与计算;应用意识.
【答案】B
【分析】根据等底等高的圆柱体积是圆锥体积的3倍,一个圆柱和一个圆锥的底面积相等,圆柱的体积是圆锥的,圆柱的高就是圆锥高的÷3=,圆柱的高是4厘米,圆锥的高是4÷,据此解答。
【解答】解:4÷(÷3)
=4÷
=36(厘米)
答:圆锥的高是36厘米。
故选:B。
【点评】本题考查的是圆柱和圆锥的体积,掌握等底等高的圆柱体积是圆锥体积的3倍是解答关键。
6.(2分)(2024秋 丰台区期末)张阿姨把10000元钱存入银行,存三年定期。按年利率1.95%计算,到期后连本带息可取出多少钱?下面列式正确的是( )
A.10000+10000×1.95%×3
B.(10000+10000×1.95%)×3
C.10000×1.95%×3
D.10000+10000×1.95%
【考点】存款利息与纳税相关问题.
【专题】应用题;应用意识.
【答案】A
【分析】利息=本金×年利率×存期,据此代入数据计算即可求出利息,再加本金即可求出到期后连本带息的钱数。
【解答】解:10000+10000×1.95%×3
=10000+585
=10585(元)
故选:A。
【点评】此题考查学生解答存款利息问题的能力。
7.(2分)(2024春 嘉祥县期中)小芳家客厅长8m,宽5.6m,画在练习本上,选比例尺( )比较合适。
A.1:100 B.1:10 C.1:1000 D.10:1
【考点】比例尺.
【专题】数感;运算能力;应用意识.
【答案】A
【分析】实际距离和比例尺已知,依据“图上距离=实际距离×比例尺”,即可求出小芳家客厅的长和宽的图上距离,再与练习本的实际长度比较即可选出合适的答案。
【解答】解:因为8米=800厘米,5.6米=560厘米
A、800×=8(厘米),560×=5.6(厘米),画在练习本比较合适;
B、800×=80(厘米),560×=56(厘米),画在练习本上,尺寸太大,不符合实际情况,故不合适;
C、800×=0.8(厘米),560×=0.56(厘米),画在练习本上尺寸太小,故不合适;
D、800×=8000(厘米),560×=5600(厘米),画在练习本上尺寸太大,故不合适。
故选:A。
【点评】此题主要考查图上距离、实际距离和比例尺的关系,解答时要注意结合实际情况。
8.(2分)(2024 扶沟县)在一个拧紧瓶盖的瓶子里装了一些水,根据图中的数据,可以算出瓶中水的体积占瓶子容积的( )
A. B. C.
【考点】圆柱的体积.
【专题】应用意识.
【答案】C
【分析】根据体积的意义可知,瓶子无论正放,还是倒放,瓶子里水的体积不变。瓶子的容积相当于以瓶子的底面为底面,高为(16﹣14+10)厘米的圆柱的容积,因为底面积不变,所以高和体积成正比例,正放时瓶子里水的高占(16﹣14+10)厘米的几分之几,也就是瓶中水的体积占瓶子容积的几分之几。据此解答即可。
【解答】解:10÷(16﹣14+10)
=10÷12
=
答:瓶中水的体积占瓶子容积的。
故选:C。
【点评】此题主要考查圆柱的体积(容积)公式的灵活运用,关键是熟记公式。
9.(2分)学校要建两个大小相同的圆柱形花坛,花坛的直径是2米,要填厚40cm的土,若每立方米的土重约750千克,那么填花坛需要土( )千克。
A.300π B.600π C.1200π D.2400π
【考点】圆柱的体积.
【专题】空间观念;应用意识.
【答案】B
【分析】根据圆柱的体积公式:V=πr2h,把数据代入公式求出填两个花坛需要土的体积,然后用土的体积乘每立方米土的质量即可。
【解答】解:40厘米=0.4米
3.14×(2÷2)2×0.4×2×750
=3.14×1×0.4×2×750
=2.512×750
=1884(千克)
答:填花坛需要土1884千克。
故选:B。
【点评】此题主要考查圆柱体积公式的灵活运用,关键是熟记公式。
10.(2分)(2025春 宝安区期中)在当今时代,芯片堪称各类电子产品的“智慧大脑”,其重要性不言而喻。有一款用于新型智能设备的长方形芯片,它实际长1.5厘米,宽0.9厘米。在技术设计图纸上,这款芯片被绘制为长6分米,宽3.6分米。那么,这张图纸的比例尺是多少呢?( )
A.1:4 B.4:1 C.1:40 D.40:1
【考点】比例尺.
【专题】推理能力;应用意识.
【答案】D
【分析】比例尺=图上距离:实际距离,根据题意可直接求得比例尺。
【解答】解:6分米:1.5厘米
=60厘米:1.5厘米
=60:1.5
=40:1
答:这张图纸的比例尺是40:1。
故选:D。
【点评】考查了比例尺的概念,掌握比例尺的计算方法,注意在求比的过程中,单位要统一。
二.填空题(共12小题,满分24分,每小题2分)
11.(2分)(2024春 黄石期中)李亮在银行存了10000元压岁钱,利率为2.25%,存满4年后,他能得利息 900 元,本息一共可以取回 10900 元。
【考点】存款利息与纳税相关问题.
【专题】应用题;应用意识.
【答案】900;10900。
【分析】先利用公式:利息=本金×利率×存期,算出利息是多少,再加本金即可。
【解答】解:10000×2.25%×4
=10000×2.25%×4
=225×4
=900(元)
10000+900=10900(元)
答:他能得利息900元,本息一共可以取回10900元。
故答案为:900;10900。
【点评】主要考查利息的计算公式:利息=本金×利率×存期。
12.(2分)(2023春 蚌山区校级期中)一根长2米,底面直径是4分米的圆柱形木料浮在水面上,如图,小华发现它正好有一半露出水面。
(1)这根木料的体积是 251.2 立方分米。
(2)这根木料露出水面部分的面积一共是 138.16 平方分米。
【考点】圆柱的侧面积、表面积和体积.
【专题】综合填空题;应用意识.
【答案】(1)251.2;(2)138.16。
【分析】(1)根据圆柱体积=底面积×高,列式计算即可;
(2)露出水面部分包括侧面积的一半和两个底面积的一半,两个底面积的一半可以拼成一个底面积,露出水面部分的面积=侧面积÷2+底面积,圆柱侧面积=底面周长×高,据此列式计算。
【解答】解:(1)2米=20分米,4÷2=2(分米)
3.14×2×2×20=251.2(立方分米)
答:体积是251.2立方分米。
(2)3.14×4×20÷2+3.14×2×2
=125.6+12.56
=138.16(平方分米)
答:这根木料露出水面部分的面积一共是138.16平方分米。
故答案为:(1)251.2;(2)138.16。
【点评】本题考查的是圆柱的侧面积、体积公式的应用。
13.(2分)(2023 武进区)小明和妈妈乘坐地铁一号线从清凉寺站到环球港站,票价4元。小明刷学生卡,可以享受五折优惠,妈妈用常州地铁APP扫码,可以享受八五折优惠。妈妈乘地铁要支付 3.4 元,小明支付的费用比妈妈便宜了。
【考点】百分数的实际应用;折扣.
【专题】应用题;应用意识.
【答案】3.4;。
【分析】五折是50%,八五折就是85%,用票价乘85%就是妈妈乘地铁需要支付的钱数;用4乘50%求出小明需要付的钱数,先求出小明比妈妈少付的钱数,再除以妈妈付的钱数即可。
【解答】解:4×85%=3.4(元)
4×50%=2(元)
(3.4﹣2)÷3.4
=2÷2.4
=
答:妈妈乘地铁要支付3.4元,小明支付的费用比妈妈便宜了。
故答案为:3.4;。
【点评】解答此题的关键是找准单位“1”的量。
14.(2分)(2024春 斗门区校级期中)一张底3dm,高5dm的直角三角形纸片,以高为轴旋转一周形成一个 圆锥 ,它的体积是 47.1 dm3。
【考点】圆锥的体积.
【专题】应用题;应用意识.
【答案】圆锥;47.1。
【分析】根据题意可知,这个直角三角形旋转一周得到的是圆锥;其中直角三角形的底是圆锥的底面半径,高是圆锥的高;根据圆锥的体积公式:体积=底面积×高×,代入数据,即可解答。
【解答】解:旋转一周形成一个圆锥。
3.14×32×5×
=3.14×3×5
=3.14×15
=47.1(dm3)
故答案为:圆锥;47.1。
【点评】此题主要考查圆锥体积公式的灵活应用,关键是熟记公式。
15.(2分)(2025春 宁乡市期中)16÷20== 4 :5= 0.8 (小数)= 80 %= 八 折。
【考点】比与分数、除法的关系;小数、分数和百分数之间的关系及其转化;折扣.
【专题】数感.
【答案】10;4;0.8;80;八。
【分析】根据分数与除法的关系16÷20=,再根据分数的基本性质,的分子、分母都除以2就是;根据比与除法的关系16÷20=16:20,再根据比的性质,比的前、后项都除以4就是4:5;16÷20=0.8;把0.8的小数点向右移动两位添上百分号就是80%;根据折扣的意义80%就是八折。
【解答】解:16÷20==4:5=0.8=80%=八折
故答案为:10;4;0.8;80;八。
【点评】此题主要是考查小数、分数、除法、比、百分数、折扣之间的关系及转化。利用它们之间的关系和性质进行转化即可。
16.(2分)(2023 通辽)如图所示,把一个棱长是12分米的正方体木料削成个最大的圆柱,圆柱的体积是 1356.48 立方分米;再把该圆柱削成一个最大的圆锥,还要再削去 904.32 立方分米。
【考点】圆柱的侧面积、表面积和体积;圆锥的体积.
【专题】立体图形的认识与计算.
【答案】1356.48,904.32。
【分析】根据题意,削成一个最大的圆柱体或最大的圆锥体的底面直径为12分米,高为12分米,可根据圆柱或圆锥的体积公式进行计算即可得到答案。
【解答】解:底面半径为:12÷2=6(分米)
圆柱的体积为:
3.14×62×12
=113.04×12
=1356.48(立方分米)
圆锥的体积为:×3.14×62×12
=3.14×36×4
=452.16(立方分米)
1356.48﹣452.16=904.32(立方分米)
答:圆柱的体积是1356.48立方分米,再将圆柱削成一个最大的圆锥,还要再削去904.32立方分米。
故答案为:1356.48,904.32。
【点评】解答此题的关键是确定削成的最大的圆柱体或圆锥体的底面直径和高,然后再根据圆柱和圆锥的体积公式进行计算即可。
17.(2分)(2024春 泰兴市期中)一个圆柱高10厘米,把它的高缩短3厘米,表面积就减少94.2平方厘米。这个圆柱原来的底面积是 78.5 平方厘米,现在的体积是 549.5 立方厘米。
【考点】圆柱的侧面积、表面积和体积.
【专题】应用意识.
【答案】78.5,549.5。
【分析】根据题意可知,把这个圆柱的高缩短3厘米,表面积减少94.2平方厘米,表面积减少的是高为3厘米的圆柱的侧面积,据此可以求出圆柱的底面半径,再根据圆的面积公式:S=πr2,圆柱的体积公式:V=Sh,把数据代入公式解答。
【解答】解:94.2÷3÷3.14÷2
=31.4÷3.14÷2
=5(厘米)
3.14×52
=3.14×25
=78.5(平方厘米)
78.5×(10﹣3)
=78.5×7
=549.5(立方厘米)
答:这个圆柱原来的面积是78.5平方厘米,现在的体积是549.5立方厘米。
故答案为:78.5,549.5。
【点评】此题主要考查圆柱的侧面积公式、体积公式的灵活运用,关键是熟记公式。
18.(2分)(2022秋 钟山区期末)学校图书室原有图书1400册,今年图书数量增加了12%。把 原有图书数量 看作单位“1”,今年图书数量是去年的 112 %。
【考点】百分数的实际应用;单位“1”的认识及确定.
【答案】原有图书数量,112。
【分析】今年图书数量增加了12%也就是今年图书增加的数量相当于原有图书量的12%,是将原有图书数量看作单位“1”,今年图书数量是去年的1+12%;据此解答。
【解答】解:1+12%=112%
学校图书室原有图书1400册,今年图书数量增加了12%。把原有图书数量看作单位“1”,今年图书数量是去年的112%。
故答案为:原有图书数量,112。
【点评】单位“1”怎么找的口诀:“是”“比”“占”“相当于”,后面就是单位“1”;“的”字前面是单位“1”。
19.(2分)(2023 甘谷县)一个圆柱的底面周长是12.56cm,高是3cm,这个圆柱的表面积是 62.8 cm2,与它等底等高的圆锥的体积是 12.56 cm3。
【考点】圆柱的侧面积、表面积和体积;圆锥的体积.
【专题】立体图形的认识与计算;空间观念;运算能力.
【答案】见试题解答内容
【分析】(1)圆柱的底面是一个圆,圆的周长公式:C=2πr,把底面周长12.56cm代入公式求出它的底面半径,然后再根据圆的面积公式:S=πr2,进行计算求出底面积;再根据圆柱的侧面积公式:S=Ch=2πrh,进行计算求出侧面积;根据圆柱的表面积=侧面积+2个底面积,求出表面积;
(2)根据圆柱的体积V=Sh=πr2h进行计算求出体积;再根据等底等高的圆锥的体积是圆柱的体积的,用圆柱的体积乘求出圆锥的体积。
【解答】解:(1)圆柱的底面半径为:12.56÷3.14÷2=2(cm)
底面积:22×3.14
=4×3.14
=12.56(cm2)
侧面积:2×3.14×2×3
=6.28×2×3
=37.68(cm2)
表面积:12.56×2+37.68
=25.12+37.68
=62.8(cm2)
(2)3.14×22×3×
=3.14×4
=12.56(cm3)
答:这个圆柱的表面积是62.8cm2,与它等底等高的圆锥的体积是12.56cm3。
故答案为:62.8;12.56。
【点评】此题主要考查圆柱的底面积、底面周长、侧面积和体积的计算,直接把数据代入它们的公式解答。
20.(2分)(2023 巨野县)如果、B都不为零),则A:B= 4 : 3 ,A与B成 正 比例。
【考点】比例的意义和基本性质.
【专题】运算能力;推理能力.
【答案】4,3;正。
【分析】先根据比例的基本性质求出A与B的比,然后求出比值,再根据比值确定A与B成什么比例。
【解答】解:由A×=B×得:
A:B
=:
=(×6):(×6)
=4:3
=
A与B的比值一定,A与B成正比例。
故答案为:4,3;正。
【点评】解答本题需熟练掌握比例的基本性质,明确化简比的方法,准确辨识两种相关联的量乘说明比例关系。
21.(2分)(2024春 商水县期中)判断下面各题中的两种量是否成比例?如果成比例,成什么比例?
(1)买足球的总价一定,买足球的个数与单价。 成反比例
(2)大米的总质量一定,吃了的和剩下的。 不成比例
(3)工作时间一定,工作总量与工作效率。 成正比例
(4)长方体的体积一定,它的底面积与高。 成反比例
【考点】辨识成正比例的量与成反比例的量.
【专题】推理能力.
【答案】(1)成反比例;(2)不成比例;(3)成正比例;(4)成反比例。
【分析】判断两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例;如果是其它的量一定或乘积、比值不一定,就不成比例。
【解答】解:(1)足球的个数×单价=足球的总价(一定);已知总价一定,也就是数量与单价的乘积一定,所以买足球的个数与单价成反比例。
(2)吃了的质量+吃剩的质量=大米的总质量(一定),是和一定,所以大米的总质量一定,吃了的质量和吃剩的质量不成比例;
(3)工作总量÷工作时间=工作效率(一定),是对应的“比值”一定,所以工作时间与工作总量成正比例;
(4)长方体的体积(一定)=它的底面积×高,它们的乘积一定,所以它的底面积与高成反比例。
故答案为:成反比例;不成比例;成正比例;成反比例。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
22.(2分)(2022 大兴区)弹簧秤可以用来称物体的质量。悬挂物体的质量不同,弹簧伸长的长度也不同。有一个弹簧秤最多能称6千克重的物体。先观察如表,再填空。
悬挂物体的质量(千克) 1 2 3 ……
弹簧伸长的长度(厘米) 3 6 9 ……
如果悬挂5千克的物体,那么弹簧伸长的长度是 15 厘米;如果弹簧伸长的长度是7.5厘米,那么悬挂物体的质量是 2.5 千克。
【考点】正、反比例应用题;数表中的规律.
【答案】15,2.5。
【分析】观察所给出的表知道,物体的重量与弹簧伸出的长度的比是1:3,由此判断物体的重量与弹簧伸长的长度成正比例,设出未知数,列出比例解答即可。
【解答】解:(1)设弹簧伸长的长度是x厘米
5:x=1:3
x=5×3
x=15
(2)设悬挂的物体重x千克
x:7.5=1:3
3x=7.5×1
x=2.5
答:弹簧伸长的长度是15厘米;悬挂的物体重2.5千克。
故答案为:15,2.5。
【点评】解答此题的关键是根据表中给出的物体的重量与弹簧伸出的长度的比值一定,得出物体的重量与弹簧伸出的长度成正比例.
三.计算题(共4小题,满分29分)
23.(8分)(2023春 零陵区期中)直接写出得数。
1.25×2.4= 10﹣10%= ×0= =
3.5÷0.2= = 2.4×= 16×0.25=
【考点】小数乘法;小数除法;分数乘法;分数除法;百分数的加减乘除运算.
【专题】运算能力.
【答案】3;9.9;0;;17.5;;2;4。
【分析】根据百分数减法、小数乘法、小数除法、分数乘法、分数加法、分数除法的计算方法直接写出得数即可。
【解答】解:
1.25×2.4=3 10﹣10%=9.9 ×0=0 =
3.5÷0.2=17.5 = 2.4×=2 16×0.25=4
【点评】本题主要考查了百分数减法、小数乘法、小数除法、分数乘法、分数加法、分数除法的运算,属于基本的计算,在平时注意积累经验,逐步提高运算的速度和准确性。
24.(12分)(2024 平桥区)脱式计算,能简算的要简算。
(1)
(2)
(3)18.67﹣(5.77+4.17)﹣4.23
(4)78×103
【考点】运算定律与简便运算;分数的四则混合运算.
【专题】运算能力.
【答案】(1)1.1;
(2)3;
(3)4.5;
(4)8034。
【分析】(1)先算小括号里面的乘法,再算小括号里面的减法,再算中括号里面的乘法,最后算中括号外面的除法;
(2)(4)根据乘法分配律进行计算;
(3)根据减法的性质进行计算。
【解答】解:(1)
=2.31÷[(4.75﹣0.25)×]
=2.31÷[4.5×]
=2.31÷2.1
=1.1
(2)
=2.25×0.6+1.75×0.6+0.6
=(2.25+1.75+1)×0.6
=5×0.6
=3
(3)18.67﹣(5.77+4.17)﹣4.23
=18.67﹣5.77﹣4.17﹣4.23
=(18.67﹣4.17)﹣(5.77+4.23)
=14.5﹣10
=4.5
(4)78×103
=78×(100+3)
=78×100+78×3
=7800+234
=8034
【点评】考查了运算定律与简便运算,四则混合运算。注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
25.(6分)(2024 郏县)解方程。
(1)
(2)
【考点】分数方程求解;解比例.
【专题】计算题;运算能力.
【答案】(1)x=240;(2)x=8。
【分析】(1),根据等式的性质1和2,两边同时+的商,再同时乘即可;
(2),根据比例的基本性质,先写成0.25x=1.25×1.6的形式,两边同时÷0.25即可。
【解答】解:(1)
x=240
(2)
0.25x=1.25×1.6
0.25x=2
0.25x÷0.25=2÷0.25
x=8
【点评】熟练掌握等式和比例的基本性质是解答本题的关键。
26.(3分)(2024 方城县)计算如图圆柱体的表面积和组合图形的体积。
(1)
(2)
【考点】圆柱的侧面积、表面积和体积;圆锥的体积.
【专题】立体图形的认识与计算;几何直观.
【答案】(1)87.92平方厘米;(2)75.36立方厘米。
【分析】(1)圆柱的表面积=侧面积+两个底面积,用字母表示:S表=2πr2+2πrh;
(2)利用圆柱的体积公式:V=πr2h,求出圆柱的体积;再利用圆锥的体积公式:V=πr2h,求出圆锥的体积,再相加即可。
【解答】解:(1)3.14×4×5+3.14×(4÷2)2×2
=3.14×20+3.14×8
=62.8+25.12
=87.92(平方厘米)
(2)3.14×(4÷2)2×5+×3.14×(4÷2)2×3
=3.14×20+3.14×4
=62.8+12.56
=75.36(立方厘米)
【点评】本题考查了圆柱体的表面积公式及体积公式及圆锥体体积公式的应用。
四.应用题题(共5小题,满分27分)
27.(4分)(2025 利通区)粮油超市十一月份卖出900桶调和油,十二月份卖出的数量比十一月份少20%,十二月份卖出多少桶调和油?
【考点】百分数的实际应用.
【专题】对应法;应用意识.
【答案】720桶。
【分析】读题可知:把十一月份卖出的900桶调和油看作单位“1”,十二月份卖出的调和油比少20%,据此列乘法算式求出它的(1﹣20%)是多少得解。
【解答】解:900×(1﹣20%)
=900×80%
=720(桶)
答:十二月份卖出720桶调和油。
【点评】本题考查了百分数的实际应用问题,解答本题时一定要清楚:单位“1”已知,用乘法作答;单位“1”未知,用除法解答。
28.(4分)(2023秋 广平县月考)石家庄到北京约是300千米,在一幅地图上两地间的距离是6厘米;在这幅地图上石家庄到南京是20厘米。请问这幅地图的比例尺是多少?石家庄到南京的实际距离是多少?
【考点】比例尺.
【专题】比和比例;应用意识.
【答案】;1000千米。
【分析】这幅地图的比例尺=图上距离:实际距离;石家庄到南京的实际距离=图上距离÷比例尺;据此解答。
【解答】解:300千米=30000000厘米
6:30000000=1:5000000
20÷÷100000
=100000000÷100000
=1000(千米)
答:这幅地图的比例尺是 ;石家庄到南京的实际距离是1000千米。
【点评】本题考查比例尺的认识以及应用,掌握应用比例尺求图上距离或实际距离的方法是解题的关键。
29.(8分)(2024 晋源区)制作一个无盖圆柱形水桶,有以下几种型号的铁皮可供搭配选择。
(1)你认为 B 和 C 的材料搭配较合适。我这样选择的原因是: 图C上下拼接后作为圆柱侧面,其底面圆半径是1分米,正好和图B圆半径匹配 。
(2)你选择的材料制作水桶的容积是 15.7 升。
【考点】圆柱的侧面积、表面积和体积.
【专题】综合填空题;应用意识.
【答案】(1)B,C,图C上下拼接后作为圆柱侧面,其底面圆半径是1分米,正好和图B圆半径匹配;(2)15.7。
【分析】(1)图A、C上下或左右拼接后作为圆柱侧面,根据圆柱展开后底面圆周长为长方形的长或宽验证数据是否匹配即可;
(2)通过(1)的选择后匹配的圆柱计算圆柱的体积,根据圆柱的体积计算公式:V=πr2h即可计算。
【解答】解:(1)图A仅知道一条长方形的宽为2分米,上下拼接作为圆柱的侧面,则2分米作为圆柱底面圆周长可知:
2÷3.14÷2≈0.03(分米),即底面圆半径约为0.03分米,图B和图D圆的半径不能和其拼成圆柱。
图B知道长方形的长和宽,上下拼接作为圆柱的侧面,则6.28分米作为圆柱底面圆周长可知:
6.28÷3.14÷2=1(分米),即底面圆半径为1分米,图B圆的半径能和其拼成圆柱。
图B知道长方形的长和宽,上下拼接作为圆柱的侧面,则5分米作为圆柱底面圆周长可知:
5÷3.14÷2≈0.80(分米),即底面圆半径约为0.03分米,图B和图D圆的半径不能和其拼成圆柱。
综上,只有C的长6.28分米作为圆柱底面圆周长时,B可以和C拼成一个圆柱。
答:我认为B和C的材料搭配较合适。我这样选择的原因是:图C上下拼接后作为圆柱侧面,其底面圆半径是1分米,正好和图B圆半径匹配。
(2)3.14×(2÷2)2×5
=3.14×5
=15.7(立方分米)
15.7立方分米=15.7升
答:水桶的容积是15.7升。
故答案为:(1)B,C,图C上下拼接后作为圆柱侧面,其底面圆半径是1分米,正好和图B圆半径匹配;(2)15.7。
【点评】本题考查了图形的拼接以及圆柱体积的计算。
30.(5分)(2023春 恩平市期中)根据条件求圆柱的表面积。(单位:厘米)
【考点】圆柱的侧面积、表面积和体积.
【专题】立体图形的认识与计算;应用意识.
【答案】351.68平方厘米。
【分析】用底面直径除以2求出圆柱底面半径,圆柱的表面积=2πr2+2πrh,代入数据计算即可解答。
【解答】解:8÷2=4(厘米)
3.14×42×2+3.14×8×10
=3.14×16×2+25.12×10
=50.24×2+251.2
=100.48+251.2
=351.68(平方厘米)
答:这个圆柱的表面积是351.68平方厘米。
【点评】此题考查圆柱表面积的计算。掌握圆柱表面积的计算公式是解答的关键。
31.(6分)(2024春 汶上县期中)居民小区的健身设施需要定期进行维护和修缮,王伯伯运来一车沙子要用来维护小区的一个沙坑。这些沙子堆成了一个圆锥形,量得底面周长是25.12米,高3米。(π取3.14)
(1)这些沙子的体积是多大?
(2)沙坑长20米、宽12.56米,需要填沙子的厚度是20厘米,这些沙子够用吗?
【考点】关于圆锥的应用题;长方体和正方体的体积.
【专题】应用意识.
【答案】(1)50.24立方米;
(2)够。
【分析】(1)根据圆锥的体积公式:V=πr2h,把数据代入公式解答。
(2)根据长方体的体积公式:V=abh,把数据代入公式求出需要沙的体积,然后与这堆沙的体积进行比较即可。
【解答】解:(1)×3.14×(25.12÷3.14÷2)2×3
=×3.14×16×3
=50.24(立方米)
答:这些沙的体积是50.24立方米。
(2)20厘米=0.2米
20×12.56×0.2
=251.2×0.2
=50.24(立方米)
50.24=50.24
答:这些沙够。
【点评】此题主要考查圆锥的体积公式、长方体的体积公式的灵活运用,关键是熟记公式。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
