【期末押题卷】北京市2024-2025学年六年级下学期数学期末测试押题预测卷一(人教版)(含解析)
文档属性
| 名称 | 【期末押题卷】北京市2024-2025学年六年级下学期数学期末测试押题预测卷一(人教版)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-06 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
北京市2024-2025学年六年级下学期数学期末测试押题预测卷
一.选择题(共10小题,满分20分,每小题2分)
1.(2分)(2023春 仓山区期中)若在数轴上表示下面各数,最左边的数是( )
A.﹣8 B.0 C.﹣3
2.(2分)(2020 博白县)如图至少是由( )个小正方体拼成的
A.6 B.12 C.10
3.(2分)(2023 洛龙区)聪聪用三根小棒围成了一个三角形,其中两根小棒的长度分别是4cm和6cm。第三根小棒的长度可能是( )
A.9cm B.10cm C.11cm D.1cm
4.(2分)(2023 吴兴区)两个连续自然数相乘的积______是偶数;两位数乘两位数时,2□×3□的积______是四位数。下列选项正确的是( )
A.可能、不可能 B.一定、不可能
C.可能、可能 D.一定、可能
5.(2分)(2024 温县)“共享经济”为我们的生活提供了便利。某辆共享单车一周的使用次数为a次,已知前6天的平均使用次数为b次/天,则第7天的使用次数是( )次。
A.6b B.a﹣6b C.b D.a+6b
6.(2分)(2023秋 滁州期末)原来学校篮球队队员的平均体重是42千克。吴奇的体重是45千克,加入篮球队后,现在篮球队队员的平均体重与原来的平均体重相比,( )
A.比原来轻 B.与原来同样重
C.比原来重
7.(2分)(2023 任泽区模拟)一张精密零件的图纸,用4厘米表示实际长度2毫米,这张图纸的比例尺为( )
A.1:20 B.20:1 C.1:2
8.(2分)(2024春 灌云县期中)下面说法中,正确的有( )句。
①如果一个圆柱的体积是一个圆锥的3倍,那么圆柱和圆锥一定等底等高;
②如果圆柱的高与它底面半径长度相等,那么圆柱体的侧面积等于两个底面积的和;
③把一个比的前项和后项都扩大3倍得到一个新的比,原来的比与新得到的比能组成比例;
④长方体、正方体和圆柱的体积都可以用“底面积×高”来计算。
A.1 B.2 C.3 D.4
9.(2分)(2022秋 右玉县期末)淘气和妹妹手拉手一起从家出发去上学,途中淘气发现忘带作业本,于是他跑回家,找到作业本后向学校飞奔而去刚好在校门口追上了妹妹。如图正确描述淘气和妹妹上学路上情景的是( )
A. B.
C.
10.(2分)(2023春 漳州期末)小英、小红、小明三人赛跑,小明说:“我不是第一名,但是比小红快。”小明是第( )名。
A.1 B.2 C.3
二.填空题(共7小题,满分14分,每小题2分)
11.(2分)(2022 椒江区)截至2022年5月,全国累计新冠疫苗接种人数达十二亿八千六百零四万九千人,这个数写作 ,把这个数改写成用“亿”作单位,且精确到百分位约为 亿。
12.(2分)(2023春 龙华区期中) ÷8== %= :24。
13.(4分)(2024秋 西固区期中)少年宫在图书馆西偏北30°200米处,则图书馆在少年宫( 偏 ) °200米处。
14.(2分)(2024秋 石狮市期末)在一次交通安全抽查中,通过某路口行人的头盔佩戴率达到90%。赵阳说:“这一时段通过这个路口的10个行人中,一定有9个行人佩戴头盔。”你同意这个说法吗?把你的想法写一写。我 (填“同意”或“不同意”),理由是: 。
15.(1分)解比例的依据是 。
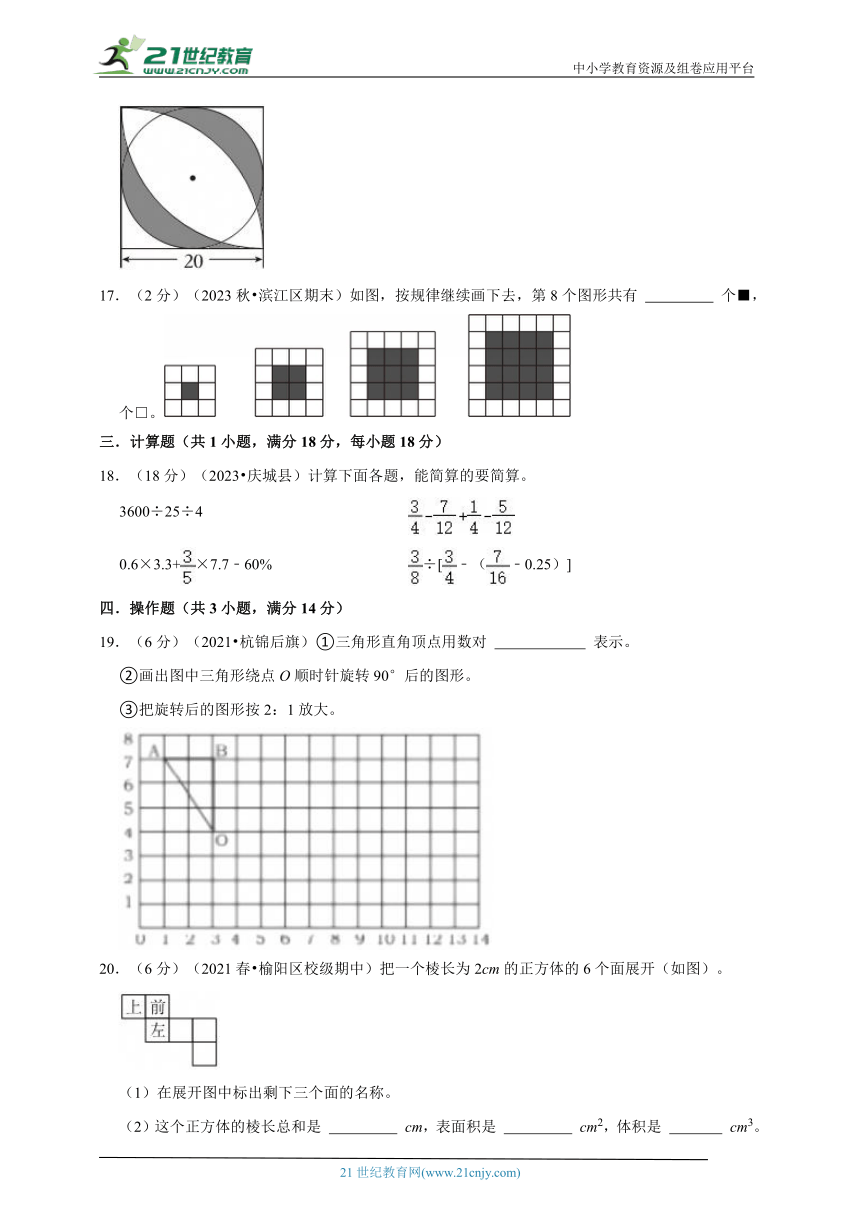
16.(1分)如图所示正方形的边长为20cm,则阴影部分面积为 平方厘米。
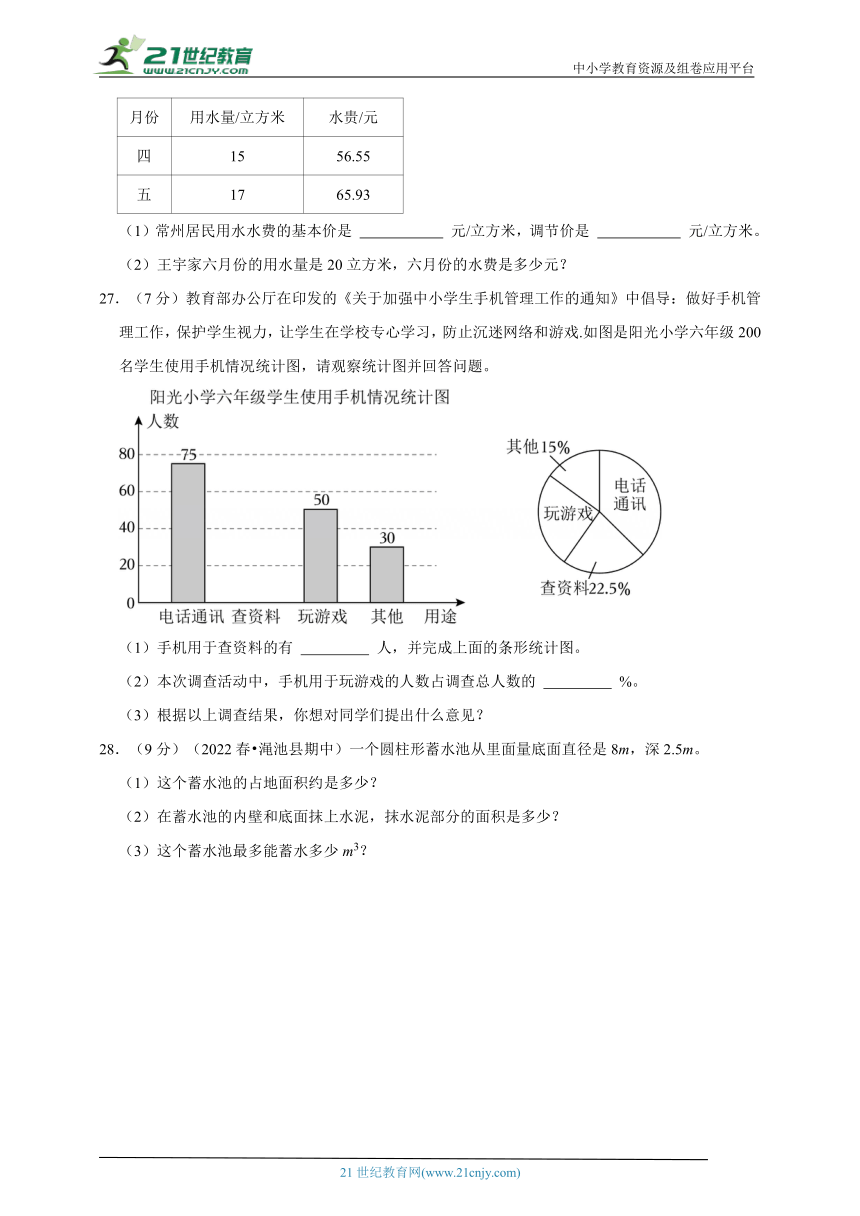
17.(2分)(2023秋 滨江区期末)如图,按规律继续画下去,第8个图形共有 个■, 个□。
三.计算题(共1小题,满分18分,每小题18分)
18.(18分)(2023 庆城县)计算下面各题,能简算的要简算。
3600÷25÷4
0.6×3.3+×7.7﹣60% ÷[﹣(﹣0.25)]
四.操作题(共3小题,满分14分)
19.(6分)(2021 杭锦后旗)①三角形直角顶点用数对 表示。
②画出图中三角形绕点O顺时针旋转90°后的图形。
③把旋转后的图形按2:1放大。
20.(6分)(2021春 榆阳区校级期中)把一个棱长为2cm的正方体的6个面展开(如图)。
(1)在展开图中标出剩下三个面的名称。
(2)这个正方体的棱长总和是 cm,表面积是 cm2,体积是 cm3。
21.(2分)(2023春 福清市期中)在学习正方体的表面积时,我们观察过正方体的展开图。现在请画出一种正方体展开图,并标明6个面的序号。
五.解答题(共7小题,满分34分)
22.(3分)(2021春 邯郸期末)将4克糖放入51克水中,糖占水的,糖占糖水的。
23.(3分)小明读一本书,已经读了全书的,如果再读24页,则读过的页数与未读的页数的比是2:3。这本书有多少页?
24.(3分)(2023秋 简阳市期末)动物运动会将要开幕,兔子家族要选拔一人去参加运动会,派谁去比较合适呢?请通过计算说明理由。
25.(3分)(2023秋 龙岩期中)实验小学四年级3个班学生去大熊猫馆参观,一班48人,二班45人,三班47人。大熊猫馆票价规定如下:
购票人数 1~50 51~100 101~150
票价(元/人) 25 20 18
四年级3个班学生购票最少要花多少元?
26.(6分)(2024 天宁区)我国是一个水资源严重短缺的国家,节约用水是每个人都应该养成的好习惯.为鼓励居民合理用水,常州规定居民用水收费标准如表①。
表①
用水量 收费方式 备注
不超过15立方米 基本价 每户以3人为计算标准。如果每户人口超过3人的,每增加1人,月用水量增加5立方米。
超过15立方米 未超过的部分仍按基本价,超过的部分按调节价收费
王宇家共有3口人,今年四、五月的用水量和水费如表②。
表②
月份 用水量/立方米 水贵/元
四 15 56.55
五 17 65.93
(1)常州居民用水水费的基本价是 元/立方米,调节价是 元/立方米。
(2)王宇家六月份的用水量是20立方米,六月份的水费是多少元?
27.(7分)教育部办公厅在印发的《关于加强中小学生手机管理工作的通知》中倡导:做好手机管理工作,保护学生视力,让学生在学校专心学习,防止沉迷网络和游戏.如图是阳光小学六年级200名学生使用手机情况统计图,请观察统计图并回答问题。
(1)手机用于查资料的有 人,并完成上面的条形统计图。
(2)本次调查活动中,手机用于玩游戏的人数占调查总人数的 %。
(3)根据以上调查结果,你想对同学们提出什么意见?
28.(9分)(2022春 渑池县期中)一个圆柱形蓄水池从里面量底面直径是8m,深2.5m。
(1)这个蓄水池的占地面积约是多少?
(2)在蓄水池的内壁和底面抹上水泥,抹水泥部分的面积是多少?
(3)这个蓄水池最多能蓄水多少m3?
北京市2024-2025学年六年级下学期数学期末测试押题预测卷
参考答案与试题解析
一.选择题(共10小题,满分20分,每小题2分)
1.(2分)(2023春 仓山区期中)若在数轴上表示下面各数,最左边的数是( )
A.﹣8 B.0 C.﹣3
【考点】数轴的认识;负数的意义及其应用.
【专题】综合题;数据分析观念.
【答案】A
【分析】数轴是规定了原点(0点)、方向和单位长度的直线,在原点(0点)左边的点所表示的数都是负数,右边的点表示的数都是正数。
【解答】解:在数轴上表示下面各数,最左边的数是﹣8。
故选:A。
【点评】此题考查了数轴的认识,要求学生能够掌握。
2.(2分)(2020 博白县)如图至少是由( )个小正方体拼成的
A.6 B.12 C.10
【考点】组合图形的计数;简单的立方体切拼问题.
【专题】空间观念.
【答案】C
【分析】从上到下,每层分别有1、3、6个小正方体,然后把个数相加即可。
【解答】解:1+3+6
=4+6
=10(个)
答:至少是由10个小正方体摆成的。
故选:C。
【点评】组合图形的计数实质上就是分类计数图形,要按顺序分类计数,防止遗漏。
3.(2分)(2023 洛龙区)聪聪用三根小棒围成了一个三角形,其中两根小棒的长度分别是4cm和6cm。第三根小棒的长度可能是( )
A.9cm B.10cm C.11cm D.1cm
【考点】三角形边的关系;三角形的特性.
【专题】平面图形的认识与计算;数据分析观念.
【答案】A
【分析】任意三角形的两边之和必须大于第三边,任意两边的差必须小于第三边,据此解答。
【解答】解:4+6=10(厘米)
6﹣4=2(厘米)
根据三角形的三边关系可知,第三边要大于2厘米小于10厘米,9厘米符合题意。
故选:A。
【点评】本题考查了三角形的三边关系的应用。
4.(2分)(2023 吴兴区)两个连续自然数相乘的积______是偶数;两位数乘两位数时,2□×3□的积______是四位数。下列选项正确的是( )
A.可能、不可能 B.一定、不可能
C.可能、可能 D.一定、可能
【考点】事件的确定性与不确定性.
【专题】可能性;应用意识.
【答案】D
【分析】两个连续自然数相乘的积一定是偶数;两位数乘两位数的积可能是三位数,有可能是四位数,据此解答。
【解答】解:两个连续自然数相乘的积一定是偶数;两位数乘两位数时,2□×3□的积可能是四位数。
故选:D。
【点评】本题考查了可能性的应用。
5.(2分)(2024 温县)“共享经济”为我们的生活提供了便利。某辆共享单车一周的使用次数为a次,已知前6天的平均使用次数为b次/天,则第7天的使用次数是( )次。
A.6b B.a﹣6b C.b D.a+6b
【考点】用字母表示数.
【专题】用字母表示数;应用意识.
【答案】B
【分析】首先求出前6天使用的总次数,用一周使用的总次数减去前6天使用的总次数即可求出第7天使用的次数。
【解答】解:6×b=6b(次)
a﹣6b=(a﹣6b)(次)
故选:B。
【点评】此题考查用字母表示数。根据题意理清数量关系,再根据用字母表示数的方法进行解答。
6.(2分)(2023秋 滁州期末)原来学校篮球队队员的平均体重是42千克。吴奇的体重是45千克,加入篮球队后,现在篮球队队员的平均体重与原来的平均体重相比,( )
A.比原来轻 B.与原来同样重
C.比原来重
【考点】平均数的含义及求平均数的方法.
【专题】平均数问题;应用意识.
【答案】C
【分析】用吴奇的体重与篮球队队员的平均体重进行比较,如果吴奇的体重大于篮球队队员的平均体重,那么现在篮球队队员的平均体重比原来的平均体重就要重;如果吴奇的体重小于篮球队队员的平均体重,那么现在篮球队队员的平均体重比原来的平均体重就要轻;据此解答。
【解答】解:45>42
答:现在篮球队队员的平均体重与原来的平均体重相比,比原来重。
故选:C。
【点评】本题考查平均数的认识以及实际应用,掌握平均数的大小与这组数据中每个数据的大小之间的关系是解题的关键。
7.(2分)(2023 任泽区模拟)一张精密零件的图纸,用4厘米表示实际长度2毫米,这张图纸的比例尺为( )
A.1:20 B.20:1 C.1:2
【考点】比例尺.
【专题】应用意识.
【答案】B
【分析】根据比例尺=图上距离:实际距离,代入数据解答即可。
【解答】解:4厘米:2毫米
=40毫米:2毫米
=40:2
=20:1
答:这张图纸的比例尺为20:1。
故选:B。
【点评】熟练掌握比例尺、图上距离、实际距离的关系是解题的关键。
8.(2分)(2024春 灌云县期中)下面说法中,正确的有( )句。
①如果一个圆柱的体积是一个圆锥的3倍,那么圆柱和圆锥一定等底等高;
②如果圆柱的高与它底面半径长度相等,那么圆柱体的侧面积等于两个底面积的和;
③把一个比的前项和后项都扩大3倍得到一个新的比,原来的比与新得到的比能组成比例;
④长方体、正方体和圆柱的体积都可以用“底面积×高”来计算。
A.1 B.2 C.3 D.4
【考点】圆柱的体积;圆锥的体积.
【专题】立体图形的认识与计算;几何直观.
【答案】C
【分析】①虽然等底等高的圆柱的体积是圆锥体积的3倍,但是一个圆柱的体积是一个圆锥的3倍,圆柱和圆锥不一定等底等高。据此判断。
②根据圆柱的侧面积公式:S=πrh,圆的面积公式:S=πr2,把数据代入公式求出圆柱的侧面积、底面积进行比较。据此判断。
③根据比例的意义,表示两个比相等的式子叫作比例。据此判断。
④根据长方体、正方体的统一体积公式:V=Sh,圆柱的体积公式:V=Sh,据此判断。
【解答】解:由分析得:
①如果一个圆柱的体积是一个圆锥的3倍,那么圆柱和圆锥一定等底等高。此说法错误。
②设圆柱的高为h,底面半径为r,
圆柱的侧面积是2πrh,
圆柱的两个底面的面积是2πr2,
2πrh=2πr2,
因此,如果圆柱的高与它底面半径长度相等,那么圆柱体的侧面积等于两个底面积的和。此说法正确。
③把一个比的前项和后项都扩大3倍得到一个新的比,原来的比与新得到的比能组成比例。此说法正确。
④长方体、正方体和圆柱的体积都可以用“底面积×高”来计算。此说法正确。
答:说法正确的有3个。
故选:C。
【点评】此题考查的目的是理解掌握等底等高的圆柱与圆锥体积之间的关系及意义,圆柱的侧面积公式、圆的面积公式及意义,比例的意义及应用,长方体、正方体、圆柱体的体积公式及应用。
9.(2分)(2022秋 右玉县期末)淘气和妹妹手拉手一起从家出发去上学,途中淘气发现忘带作业本,于是他跑回家,找到作业本后向学校飞奔而去刚好在校门口追上了妹妹。如图正确描述淘气和妹妹上学路上情景的是( )
A. B.
C.
【考点】简单的行程问题.
【专题】数据分析观念;应用意识.
【答案】A
【分析】根据题意可知,妹妹没有停留一直走到学校,所以表示妹妹行走的图象是一条直线,淘气和妹妹一起去上学,所以他们一开始的图象是重合在一起的,途中淘气发现忘带作业本,于是他跑回家,拿好作业本,表示淘气行走的图象是一条折线,且在家中拿作业本这段时间形走的距离不变,然后马上向学校飞奔而去,刚好在校门口追上了妹妹。这时表示他们两人行走的图象交于一点,据此对照下面的图象进行选择即可。
【解答】解:由分析得:所以表示妹妹行走的图象是一条直线,表示淘气行走的图象,途中返回是折线,且在家中拿作业本这段时间形走的距离不变,然后马上向学校飞奔而去,刚好在校门口追上了妹妹。这时表示他们两人行走的图象交于一点。由此可知,图A描述的是淘气和妹妹上学路上的情景。
故选:A。
【点评】此题考查的目的是理解掌握复式折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
10.(2分)(2023春 漳州期末)小英、小红、小明三人赛跑,小明说:“我不是第一名,但是比小红快。”小明是第( )名。
A.1 B.2 C.3
【考点】逻辑推理.
【专题】压轴题;推理能力.
【答案】B
【分析】小明说:“我不是第一名,但是比小红快。”说明小明处在中间,即第二名,据此解答即可。
【解答】解:小明说:“我不是第一名,但是比小红快。”说明小明既不是第一名,也不是第三名,即第二名。
答:小明是第2名。
故选:B。
【点评】本题考查了简单的逻辑推理问题。
二.填空题(共7小题,满分14分,每小题2分)
11.(2分)(2022 椒江区)截至2022年5月,全国累计新冠疫苗接种人数达十二亿八千六百零四万九千人,这个数写作 1286049000 ,把这个数改写成用“亿”作单位,且精确到百分位约为 13 亿。
【考点】亿以上数的读写;亿以上数的改写与近似.
【专题】数感.
【答案】1286049000,13。
【分析】整数的写法:从高位到低位,一级一级地写,哪一个数位上一个单位也没有,就在那个数位上写0。
通过四舍五入法求整数的近似数,要对省略的尾数部分的最高位上的数进行四舍五入,若小于5则直接舍去,若大于或等于5,则向前一位进一,并加上“亿”。
【解答】解:截至2022年5月,全国累计新冠疫苗接种人数达十二亿八千六百零四万九千人,这个数写作:1286049000,把这个数改写成用“亿”作单位,且精确到百分位约为13亿。
故答案为:1286049000,13。
【点评】熟练掌握整数写法、整数的改写及近似数的求法,是解答此题的关键。
12.(2分)(2023春 龙华区期中) 6 ÷8== 75 %= 18 :24。
【考点】比与分数、除法的关系.
【专题】分数和百分数;数据分析观念.
【答案】6,75,18。
【分析】解答此题的关键是,根据分数的基本性质,分子、分母都乘6就是,根据比与分数的关系=18:24;根据分数与除法的关系,=3÷4,再根据商不变的性质,被除数、除数都乘2就是6÷8;=3÷4=0.75,把0.75的小数点向右移动两位,添上百分号就是75%,由此进行转化并填空。
【解答】解:6÷8==75%=18:24。
故答案为:6,75,18。
【点评】此题主要是考查除法、小数、分数、百分数、比之间的关系及转化,利用它们之间的关系和性质进行转化即可。
13.(4分)(2024秋 西固区期中)少年宫在图书馆西偏北30°200米处,则图书馆在少年宫( 东 偏 南 ) 30 °200米处。
【考点】根据方向和距离确定物体的位置.
【专题】综合题;空间观念.
【答案】东,南,30。
【分析】两个位置是相对的,分别以它们为观察中心时,看到对方的方向相反,角度和距离相等。
【解答】解:少年宫在图书馆西偏北30°200米处,则图书馆在少年宫东偏南30°200米处。
故答案为:东,南,30。
【点评】本题考查的是根据方向和距离确定物体位置的应用。
14.(2分)(2024秋 石狮市期末)在一次交通安全抽查中,通过某路口行人的头盔佩戴率达到90%。赵阳说:“这一时段通过这个路口的10个行人中,一定有9个行人佩戴头盔。”你同意这个说法吗?把你的想法写一写。我 不同意 (填“同意”或“不同意”),理由是: 90%的头盔佩戴率是一个统计结果,如果观察较多的行人,大约90%的人会佩戴头盔。如果任意选取其中10个行人,那么不一定是9个人佩戴头盔 。
【考点】百分率应用题.
【专题】综合填空题;数据分析观念.
【答案】不同意,90%的头盔佩戴率是一个统计结果,如果观察较多的行人,大约90%的人会佩戴头盔。如果任意选取其中10个行人,那么不一定是9个人佩戴头盔(答案不唯一)。
【分析】百分率表示一个数是另一个数的百分之几的数,通常用百分号(%)来表示;用百分数的形式来表示两个数的比值,据此解答。
【解答】解:我不同意,理由是:90%的头盔佩戴率是一个统计结果,如果观察较多的行人,大约90%的人会佩戴头盔。如果任意选取其中10个行人,那么不一定是9个人佩戴头盔(答案不唯一)。
故答案为:不同意,90%的头盔佩戴率是一个统计结果,如果观察较多的行人,大约90%的人会佩戴头盔。如果任意选取其中10个行人,那么不一定是9个人佩戴头盔(答案不唯一)。
【点评】此题考查了百分率的知识,要求学生掌握。
15.(1分)解比例的依据是 比例的基本性质 。
【考点】解比例.
【专题】比和比例;运算能力.
【答案】比例的基本性质。
【分析】根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个比例中的另外一个未知项。求比例中的未知项,叫做解比例,所以解比例的依据是比例的基本性质。
【解答】解:解比例的依据是比例的基本性质。
故答案为:比例的基本性质。
【点评】此题主要考查了解比例问题,要熟练掌握,注意比例的基本性质的应用。
16.(1分)如图所示正方形的边长为20cm,则阴影部分面积为 129 平方厘米。
【考点】圆与组合图形.
【专题】几何直观.
【答案】129。
【分析】根据图形的特点,边长为20厘米的正方形面积减去半径为20厘米的圆面积的是图中①、②的面积和;
边长为20厘米的正方形面积减去直径为20厘米的圆的面积,然后除以4等于图中①的面积;
然后用①、②的面积和减去①的面积,再乘2就是阴影部分的面积,据此列式解答。
【解答】解:如图:
20×20﹣3.14×202×
=400﹣314
=86(平方厘米)
[20×20﹣3.14×(20÷2)2]÷4
=[400﹣3.14×100]÷4
=[400﹣314]÷4
=86÷4
=21.5(平方厘米)
(86﹣21.5)×2
=64.5×2
=129(平方厘米)
答:阴影部分的面积是129平方厘米。
故答案为:129。
【点评】本题考查了圆与组合图形面积计算知识,解答这类问题,关键是观察分析图形是由哪几部分组成的,是求各部分的面积和、还是求各部分的面积差,再根据相应的面积公式解答即可。
17.(2分)(2023秋 滨江区期末)如图,按规律继续画下去,第8个图形共有 64 个■, 36 个□。
【考点】数与形结合的规律.
【专题】推理能力;模型思想.
【答案】64;36。
【分析】通过数形结合的规律解答此题。观察图形,可得出如下规律:第1个有:,1×1个■,3×3﹣1×1个□;第2个有:2×2个■,4×4﹣2×2个□;第3个有:3×3个■,5×5﹣3×3个□;第4个有:4×4个■,6×6﹣4×4个□;……
以此类推:第n个有:n×n个■,(n+2)×(n+2)﹣n×n个□。据此解答。
【解答】解:观察图形,可得出如下规律:
第1个有:,1×1个■,3×3﹣1×1个□;
第2个有:2×2个■,4×4﹣2×2个□;
第3个有:3×3个■,5×5﹣3×3个□;
第4个有:4×4个■,6×6﹣4×4个□;
……
以此类推:
第n个有:n×n个■,(n+2)×(n+2)﹣n×n个□;
第8个有:8×8=64个■,(8+2)×(8+2)﹣8×8=36个□。
答:第8个图形共有64个■,36个□。
故答案为:64;36。
【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力。
三.计算题(共1小题,满分18分,每小题18分)
18.(18分)(2023 庆城县)计算下面各题,能简算的要简算。
3600÷25÷4
0.6×3.3+×7.7﹣60% ÷[﹣(﹣0.25)]
【考点】整数、分数、小数、百分数四则混合运算;运算定律与简便运算;分数的四则混合运算.
【专题】运算能力.
【答案】36,0,6,。
【分析】(1)根据除法的性质简算;
(2)根据加法交换律和减法的性质简算;
(3)根据乘法分配律简算;
(4)先根据减法的性质简算,再算括号外的除法。
【解答】解:(1)3600÷25÷4
=3600÷(25×4)
=3600÷100
=36
(2)
=(+)﹣(+)
=1﹣1
=0
(3)0.6×3.3+×7.7﹣60%
=0.6×(3.3+7.7﹣1)
=0.6×10
=6
(4)÷[﹣(﹣0.25)]
=÷[+0.25﹣]
=÷[1﹣]
=÷
=
【点评】本题考查了四则混合运算,注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
四.操作题(共3小题,满分14分)
19.(6分)(2021 杭锦后旗)①三角形直角顶点用数对 (3,7) 表示。
②画出图中三角形绕点O顺时针旋转90°后的图形。
③把旋转后的图形按2:1放大。
【考点】数对与位置;作旋转一定角度后的图形;图形的放大与缩小.
【专题】几何直观;应用意识.
【答案】①(3,7);
②如图:
③如图:
【分析】①根据利用数对表示物体位置的方法,用数对表示物体的位置时,列数在前,行数在后。据此用数对表示出直角三角形直角顶点的位置。
②根据图形旋转的性质,图形旋转后,图形的形状和大小不变,只是图形的位置发生了变化。据此画出图中三角形绕点O顺时针旋转90°后的图形。
③根据图形放大的方法,下求出放大2倍后,三角形的底和高各是多少,据此画出放大后的三角形。据此解答。
【解答】解:①三角形直角顶点用数对(3,7)表示。
②将直角三角形ABO绕点O顺时针旋转90°。作图如下:
③放大后三角形的底是:2×2=4
放大后三角形的高是:3×2=6
作图如下:
故答案为:(3,7)。
【点评】此题考查的目的是理解掌握利用数对表示物体位置的方法及应用,图形旋转的性质、图形放大的方法及应用。
20.(6分)(2021春 榆阳区校级期中)把一个棱长为2cm的正方体的6个面展开(如图)。
(1)在展开图中标出剩下三个面的名称。
(2)这个正方体的棱长总和是 24 cm,表面积是 24 cm2,体积是 8 cm3。
【考点】正方体的展开图;长方体和正方体的表面积;长方体和正方体的体积.
【专题】空间观念;几何直观;应用意识.
【答案】(1);
(2)24,24,8。
【分析】(1)此图属于正方体展开图的“1﹣3﹣2”型,折成正方体后,第一行的左边一个正方形(标有“上”)与第二行的中间一个正方形相对;上行的第二个正方形(标有“前”)与第三行的正方形相对;第二行的第一个正方形(标有“左”)的正方形与本行的第三个正方形相对。根据“前﹣后、左﹣右、上﹣下”即可在图中标出剩下三个面的名称。
(2)正方体有12条相等的棱,每条棱的长度乘12,就是这个正方体的棱长总和;根据正方体的表面积计算公式“S=6a2”即可求出这个正方体的表面积;根据正方体的体积计算公式“V=a3”即可求出这个正方体的体积。
【解答】解:(1)
(2)2×12=24(cm)
2×2×6=24(cm2)
2×2×2=8(cm3)
答:这个正方体的棱长总和是24cm,表面积是24cm2,体积是8cm3。
故答案为:24,24,8。
【点评】此题考查的知识点:正方体展开图、正方体的特征、正方体表面积的计算、正方体体积的计算。
21.(2分)(2023春 福清市期中)在学习正方体的表面积时,我们观察过正方体的展开图。现在请画出一种正方体展开图,并标明6个面的序号。
【考点】正方体的展开图.
【专题】空间观念;几何直观.
【答案】(答案不唯一)。
【分析】画法不唯一。根据正方体展开图的11种特征,即可画出一种正方体展开图,并标明6个面的序号。
【解答】解:
(答案不唯一)。
【点评】此题是考查正方体展开图的认识。正方体展开图分四种类型,11种情况,要掌握每种情况的特征。每种情况,哪些面相对是有规律的,也要掌握。
五.解答题(共7小题,满分34分)
22.(3分)(2021春 邯郸期末)将4克糖放入51克水中,糖占水的,糖占糖水的。
【考点】部分占总数的几分之几.
【专题】分数和百分数;数据分析观念.
【答案】,。
【分析】利用糖的质量除以水的质量,利用糖加水求出糖水的质量,再利用糖的质量除以糖水的质量即可。
【解答】解:4÷51=
4÷(4+51)
=4÷55
=
答:糖占水的,糖占糖水的。
故答案为:,。
【点评】本题考查了一个数占另一个数的几分之几的解答方法。
23.(3分)小明读一本书,已经读了全书的,如果再读24页,则读过的页数与未读的页数的比是2:3。这本书有多少页?
【考点】比的应用.
【专题】比和比例.
【答案】160页。
【分析】读过的页数与未读的页数的比是2:3,则读过的页数占总页数的,24页对应的分率是(﹣),求总页数,用除法即可。
【解答】解:由读过的页数与未读的页数的比是2:3,
得,24÷(﹣)
=24÷
=160(页)
答:这本书有160页。
【点评】本题是一道有关比的应用、分数的混合运算的题目。
24.(3分)(2023秋 简阳市期末)动物运动会将要开幕,兔子家族要选拔一人去参加运动会,派谁去比较合适呢?请通过计算说明理由。
【考点】简单的行程问题.
【专题】应用题;数据分析观念.
【答案】黑兔子。
【分析】根据“速度=路程÷时间”,先求出白兔子和黑兔子的速度,进而比较它们的速度,选出速度快的兔子参加运动会。
【解答】解:白兔子:64.8÷8=8.1(米/秒)
黑兔子:136÷16=8.5(米/秒)
8.5>8.1
答:派黑兔子去比较合适。
【点评】此题主要考查路程、速度、时间三者的关系式:路程=速度×时间,速度=路程÷时间,时间=路程÷速度,灵活变形列式解决问题。
25.(3分)(2023秋 龙岩期中)实验小学四年级3个班学生去大熊猫馆参观,一班48人,二班45人,三班47人。大熊猫馆票价规定如下:
购票人数 1~50 51~100 101~150
票价(元/人) 25 20 18
四年级3个班学生购票最少要花多少元?
【考点】最优化问题.
【专题】应用题;应用意识.
【答案】2520元。
【分析】根据价格表可知,购票人数越多,票价越低,即3个班级应合起来一起买票。据此解答。
【解答】解:48+45+47=140(人)
140×18=2520(元)
答:四年级3个班学生购票最少要花2520元。
【点评】本题考查了最优化问题的应用。
26.(6分)(2024 天宁区)我国是一个水资源严重短缺的国家,节约用水是每个人都应该养成的好习惯.为鼓励居民合理用水,常州规定居民用水收费标准如表①。
表①
用水量 收费方式 备注
不超过15立方米 基本价 每户以3人为计算标准。如果每户人口超过3人的,每增加1人,月用水量增加5立方米。
超过15立方米 未超过的部分仍按基本价,超过的部分按调节价收费
王宇家共有3口人,今年四、五月的用水量和水费如表②。
表②
月份 用水量/立方米 水贵/元
四 15 56.55
五 17 65.93
(1)常州居民用水水费的基本价是 3.77 元/立方米,调节价是 4.69 元/立方米。
(2)王宇家六月份的用水量是20立方米,六月份的水费是多少元?
【考点】整数、小数复合应用题.
【专题】综合题;应用意识.
【答案】(1)3.77;4.69。(2)80元。
【分析】(1)根据题意,未超过15立方米时,水费按“基本价”收费,四月份用15立方米未超过15立方米,水费是56.55元,用56.55除以15求出“基本价”;五月份超过15立方米,超出17﹣15=2(立方米),用五月份水费的钱数﹣15立方米的水费钱数,求出超出部分的钱数,再除以超出2立方米即可求出“调节价”;(2)20立方米水分成两部分计算,用15立方米的水费钱数加上超出(20﹣15)立方米的钱数即可。
【解答】解:(1)56.55÷15=3.77(元/立方米)
(65.93﹣56.55)÷(17﹣15)
=9.38÷2
=4.69(元/立方米)
答:常州居民用水水费的基本价是3.77元/立方米,调节价是4.69元/立方米。
(2)56.55+(20﹣15)×4.69
=56.55+5×4.69
=56.55+23.45
=80(元)
答:六月份的水费是80元。
故答案为:3.77;4.69。
【点评】本题考查整数小数复合应用,熟练掌握单价×数量=总价,分段计费的计算方法是解答本题的关键。
27.(7分)教育部办公厅在印发的《关于加强中小学生手机管理工作的通知》中倡导:做好手机管理工作,保护学生视力,让学生在学校专心学习,防止沉迷网络和游戏.如图是阳光小学六年级200名学生使用手机情况统计图,请观察统计图并回答问题。
(1)手机用于查资料的有 45 人,并完成上面的条形统计图。
(2)本次调查活动中,手机用于玩游戏的人数占调查总人数的 25 %。
(3)根据以上调查结果,你想对同学们提出什么意见?
【考点】统计图表的填补;从统计图表中获取信息;扇形统计图.
【专题】数据分析观念;应用意识.
【答案】(1)45;
(2)25;
(3)减少玩手机游戏时间,保护视力。(答案不唯一)
【分析】(1)手机用于查资料的人数=调查总人数200×查资料的人数占总人数的百分率,然后补全条形统计图;
(2)手机用于玩游戏的人数占调查总人数的百分率=手机用于玩游戏的人数÷调查总人数×100%;
(3)建议减少玩手机游戏时间,保护视力。(答案不唯一)
【解答】解:(1)200×22.5%
=200×0.225
=45(人)
(2)50÷200×100%
=0.25×100%
=25%
答:手机用于玩游戏的人数占调查总人数的25%。
(3)建议减少玩手机游戏时间,保护视力。(答案不唯一)
故答案为:45;25。
【点评】本题关键是先读懂扇形统计图,找出各个量之间的关系,再把这一关系在条形统计图上表示出来。
28.(9分)(2022春 渑池县期中)一个圆柱形蓄水池从里面量底面直径是8m,深2.5m。
(1)这个蓄水池的占地面积约是多少?
(2)在蓄水池的内壁和底面抹上水泥,抹水泥部分的面积是多少?
(3)这个蓄水池最多能蓄水多少m3?
【考点】关于圆柱的应用题.
【专题】空间观念;应用意识.
【答案】(1)50.24平方米;
(2)113.04平方米;
(3)125.6立方米。
【分析】(1)根据圆的面积公式:S=πr2,把数据代入公式解答。
(2)因为水池无盖,所以抹水泥部分的面积是这个圆柱的一个底面的面积加上侧面积,根据圆的面积公式:S=πr2,圆柱的侧面积公式:S=πdh,把数据代入公式解答。
(3)根据圆柱的容积(体积)公式:V=Sh,把数据代入公式解答。
【解答】解:(1)3.14×(8÷2)2
=3.14×16
=50.24(平方米)
答:这个蓄水池的占地面积是50.24平方米。
(2)50.24+3.14×8×2.5
=50.24+62.8
=113.04(平方米)
答:抹水泥的面积是113.04平方米。
(3)50.24×2.5=125.6(立方米)
答:这个蓄水池最多能蓄水125.6立方米。
【点评】此题主要考查圆的面积公式、圆柱的侧面积公式、圆柱的体积公式在实际生活中的应用,关键是熟记公式。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
北京市2024-2025学年六年级下学期数学期末测试押题预测卷
一.选择题(共10小题,满分20分,每小题2分)
1.(2分)(2023春 仓山区期中)若在数轴上表示下面各数,最左边的数是( )
A.﹣8 B.0 C.﹣3
2.(2分)(2020 博白县)如图至少是由( )个小正方体拼成的
A.6 B.12 C.10
3.(2分)(2023 洛龙区)聪聪用三根小棒围成了一个三角形,其中两根小棒的长度分别是4cm和6cm。第三根小棒的长度可能是( )
A.9cm B.10cm C.11cm D.1cm
4.(2分)(2023 吴兴区)两个连续自然数相乘的积______是偶数;两位数乘两位数时,2□×3□的积______是四位数。下列选项正确的是( )
A.可能、不可能 B.一定、不可能
C.可能、可能 D.一定、可能
5.(2分)(2024 温县)“共享经济”为我们的生活提供了便利。某辆共享单车一周的使用次数为a次,已知前6天的平均使用次数为b次/天,则第7天的使用次数是( )次。
A.6b B.a﹣6b C.b D.a+6b
6.(2分)(2023秋 滁州期末)原来学校篮球队队员的平均体重是42千克。吴奇的体重是45千克,加入篮球队后,现在篮球队队员的平均体重与原来的平均体重相比,( )
A.比原来轻 B.与原来同样重
C.比原来重
7.(2分)(2023 任泽区模拟)一张精密零件的图纸,用4厘米表示实际长度2毫米,这张图纸的比例尺为( )
A.1:20 B.20:1 C.1:2
8.(2分)(2024春 灌云县期中)下面说法中,正确的有( )句。
①如果一个圆柱的体积是一个圆锥的3倍,那么圆柱和圆锥一定等底等高;
②如果圆柱的高与它底面半径长度相等,那么圆柱体的侧面积等于两个底面积的和;
③把一个比的前项和后项都扩大3倍得到一个新的比,原来的比与新得到的比能组成比例;
④长方体、正方体和圆柱的体积都可以用“底面积×高”来计算。
A.1 B.2 C.3 D.4
9.(2分)(2022秋 右玉县期末)淘气和妹妹手拉手一起从家出发去上学,途中淘气发现忘带作业本,于是他跑回家,找到作业本后向学校飞奔而去刚好在校门口追上了妹妹。如图正确描述淘气和妹妹上学路上情景的是( )
A. B.
C.
10.(2分)(2023春 漳州期末)小英、小红、小明三人赛跑,小明说:“我不是第一名,但是比小红快。”小明是第( )名。
A.1 B.2 C.3
二.填空题(共7小题,满分14分,每小题2分)
11.(2分)(2022 椒江区)截至2022年5月,全国累计新冠疫苗接种人数达十二亿八千六百零四万九千人,这个数写作 ,把这个数改写成用“亿”作单位,且精确到百分位约为 亿。
12.(2分)(2023春 龙华区期中) ÷8== %= :24。
13.(4分)(2024秋 西固区期中)少年宫在图书馆西偏北30°200米处,则图书馆在少年宫( 偏 ) °200米处。
14.(2分)(2024秋 石狮市期末)在一次交通安全抽查中,通过某路口行人的头盔佩戴率达到90%。赵阳说:“这一时段通过这个路口的10个行人中,一定有9个行人佩戴头盔。”你同意这个说法吗?把你的想法写一写。我 (填“同意”或“不同意”),理由是: 。
15.(1分)解比例的依据是 。
16.(1分)如图所示正方形的边长为20cm,则阴影部分面积为 平方厘米。
17.(2分)(2023秋 滨江区期末)如图,按规律继续画下去,第8个图形共有 个■, 个□。
三.计算题(共1小题,满分18分,每小题18分)
18.(18分)(2023 庆城县)计算下面各题,能简算的要简算。
3600÷25÷4
0.6×3.3+×7.7﹣60% ÷[﹣(﹣0.25)]
四.操作题(共3小题,满分14分)
19.(6分)(2021 杭锦后旗)①三角形直角顶点用数对 表示。
②画出图中三角形绕点O顺时针旋转90°后的图形。
③把旋转后的图形按2:1放大。
20.(6分)(2021春 榆阳区校级期中)把一个棱长为2cm的正方体的6个面展开(如图)。
(1)在展开图中标出剩下三个面的名称。
(2)这个正方体的棱长总和是 cm,表面积是 cm2,体积是 cm3。
21.(2分)(2023春 福清市期中)在学习正方体的表面积时,我们观察过正方体的展开图。现在请画出一种正方体展开图,并标明6个面的序号。
五.解答题(共7小题,满分34分)
22.(3分)(2021春 邯郸期末)将4克糖放入51克水中,糖占水的,糖占糖水的。
23.(3分)小明读一本书,已经读了全书的,如果再读24页,则读过的页数与未读的页数的比是2:3。这本书有多少页?
24.(3分)(2023秋 简阳市期末)动物运动会将要开幕,兔子家族要选拔一人去参加运动会,派谁去比较合适呢?请通过计算说明理由。
25.(3分)(2023秋 龙岩期中)实验小学四年级3个班学生去大熊猫馆参观,一班48人,二班45人,三班47人。大熊猫馆票价规定如下:
购票人数 1~50 51~100 101~150
票价(元/人) 25 20 18
四年级3个班学生购票最少要花多少元?
26.(6分)(2024 天宁区)我国是一个水资源严重短缺的国家,节约用水是每个人都应该养成的好习惯.为鼓励居民合理用水,常州规定居民用水收费标准如表①。
表①
用水量 收费方式 备注
不超过15立方米 基本价 每户以3人为计算标准。如果每户人口超过3人的,每增加1人,月用水量增加5立方米。
超过15立方米 未超过的部分仍按基本价,超过的部分按调节价收费
王宇家共有3口人,今年四、五月的用水量和水费如表②。
表②
月份 用水量/立方米 水贵/元
四 15 56.55
五 17 65.93
(1)常州居民用水水费的基本价是 元/立方米,调节价是 元/立方米。
(2)王宇家六月份的用水量是20立方米,六月份的水费是多少元?
27.(7分)教育部办公厅在印发的《关于加强中小学生手机管理工作的通知》中倡导:做好手机管理工作,保护学生视力,让学生在学校专心学习,防止沉迷网络和游戏.如图是阳光小学六年级200名学生使用手机情况统计图,请观察统计图并回答问题。
(1)手机用于查资料的有 人,并完成上面的条形统计图。
(2)本次调查活动中,手机用于玩游戏的人数占调查总人数的 %。
(3)根据以上调查结果,你想对同学们提出什么意见?
28.(9分)(2022春 渑池县期中)一个圆柱形蓄水池从里面量底面直径是8m,深2.5m。
(1)这个蓄水池的占地面积约是多少?
(2)在蓄水池的内壁和底面抹上水泥,抹水泥部分的面积是多少?
(3)这个蓄水池最多能蓄水多少m3?
北京市2024-2025学年六年级下学期数学期末测试押题预测卷
参考答案与试题解析
一.选择题(共10小题,满分20分,每小题2分)
1.(2分)(2023春 仓山区期中)若在数轴上表示下面各数,最左边的数是( )
A.﹣8 B.0 C.﹣3
【考点】数轴的认识;负数的意义及其应用.
【专题】综合题;数据分析观念.
【答案】A
【分析】数轴是规定了原点(0点)、方向和单位长度的直线,在原点(0点)左边的点所表示的数都是负数,右边的点表示的数都是正数。
【解答】解:在数轴上表示下面各数,最左边的数是﹣8。
故选:A。
【点评】此题考查了数轴的认识,要求学生能够掌握。
2.(2分)(2020 博白县)如图至少是由( )个小正方体拼成的
A.6 B.12 C.10
【考点】组合图形的计数;简单的立方体切拼问题.
【专题】空间观念.
【答案】C
【分析】从上到下,每层分别有1、3、6个小正方体,然后把个数相加即可。
【解答】解:1+3+6
=4+6
=10(个)
答:至少是由10个小正方体摆成的。
故选:C。
【点评】组合图形的计数实质上就是分类计数图形,要按顺序分类计数,防止遗漏。
3.(2分)(2023 洛龙区)聪聪用三根小棒围成了一个三角形,其中两根小棒的长度分别是4cm和6cm。第三根小棒的长度可能是( )
A.9cm B.10cm C.11cm D.1cm
【考点】三角形边的关系;三角形的特性.
【专题】平面图形的认识与计算;数据分析观念.
【答案】A
【分析】任意三角形的两边之和必须大于第三边,任意两边的差必须小于第三边,据此解答。
【解答】解:4+6=10(厘米)
6﹣4=2(厘米)
根据三角形的三边关系可知,第三边要大于2厘米小于10厘米,9厘米符合题意。
故选:A。
【点评】本题考查了三角形的三边关系的应用。
4.(2分)(2023 吴兴区)两个连续自然数相乘的积______是偶数;两位数乘两位数时,2□×3□的积______是四位数。下列选项正确的是( )
A.可能、不可能 B.一定、不可能
C.可能、可能 D.一定、可能
【考点】事件的确定性与不确定性.
【专题】可能性;应用意识.
【答案】D
【分析】两个连续自然数相乘的积一定是偶数;两位数乘两位数的积可能是三位数,有可能是四位数,据此解答。
【解答】解:两个连续自然数相乘的积一定是偶数;两位数乘两位数时,2□×3□的积可能是四位数。
故选:D。
【点评】本题考查了可能性的应用。
5.(2分)(2024 温县)“共享经济”为我们的生活提供了便利。某辆共享单车一周的使用次数为a次,已知前6天的平均使用次数为b次/天,则第7天的使用次数是( )次。
A.6b B.a﹣6b C.b D.a+6b
【考点】用字母表示数.
【专题】用字母表示数;应用意识.
【答案】B
【分析】首先求出前6天使用的总次数,用一周使用的总次数减去前6天使用的总次数即可求出第7天使用的次数。
【解答】解:6×b=6b(次)
a﹣6b=(a﹣6b)(次)
故选:B。
【点评】此题考查用字母表示数。根据题意理清数量关系,再根据用字母表示数的方法进行解答。
6.(2分)(2023秋 滁州期末)原来学校篮球队队员的平均体重是42千克。吴奇的体重是45千克,加入篮球队后,现在篮球队队员的平均体重与原来的平均体重相比,( )
A.比原来轻 B.与原来同样重
C.比原来重
【考点】平均数的含义及求平均数的方法.
【专题】平均数问题;应用意识.
【答案】C
【分析】用吴奇的体重与篮球队队员的平均体重进行比较,如果吴奇的体重大于篮球队队员的平均体重,那么现在篮球队队员的平均体重比原来的平均体重就要重;如果吴奇的体重小于篮球队队员的平均体重,那么现在篮球队队员的平均体重比原来的平均体重就要轻;据此解答。
【解答】解:45>42
答:现在篮球队队员的平均体重与原来的平均体重相比,比原来重。
故选:C。
【点评】本题考查平均数的认识以及实际应用,掌握平均数的大小与这组数据中每个数据的大小之间的关系是解题的关键。
7.(2分)(2023 任泽区模拟)一张精密零件的图纸,用4厘米表示实际长度2毫米,这张图纸的比例尺为( )
A.1:20 B.20:1 C.1:2
【考点】比例尺.
【专题】应用意识.
【答案】B
【分析】根据比例尺=图上距离:实际距离,代入数据解答即可。
【解答】解:4厘米:2毫米
=40毫米:2毫米
=40:2
=20:1
答:这张图纸的比例尺为20:1。
故选:B。
【点评】熟练掌握比例尺、图上距离、实际距离的关系是解题的关键。
8.(2分)(2024春 灌云县期中)下面说法中,正确的有( )句。
①如果一个圆柱的体积是一个圆锥的3倍,那么圆柱和圆锥一定等底等高;
②如果圆柱的高与它底面半径长度相等,那么圆柱体的侧面积等于两个底面积的和;
③把一个比的前项和后项都扩大3倍得到一个新的比,原来的比与新得到的比能组成比例;
④长方体、正方体和圆柱的体积都可以用“底面积×高”来计算。
A.1 B.2 C.3 D.4
【考点】圆柱的体积;圆锥的体积.
【专题】立体图形的认识与计算;几何直观.
【答案】C
【分析】①虽然等底等高的圆柱的体积是圆锥体积的3倍,但是一个圆柱的体积是一个圆锥的3倍,圆柱和圆锥不一定等底等高。据此判断。
②根据圆柱的侧面积公式:S=πrh,圆的面积公式:S=πr2,把数据代入公式求出圆柱的侧面积、底面积进行比较。据此判断。
③根据比例的意义,表示两个比相等的式子叫作比例。据此判断。
④根据长方体、正方体的统一体积公式:V=Sh,圆柱的体积公式:V=Sh,据此判断。
【解答】解:由分析得:
①如果一个圆柱的体积是一个圆锥的3倍,那么圆柱和圆锥一定等底等高。此说法错误。
②设圆柱的高为h,底面半径为r,
圆柱的侧面积是2πrh,
圆柱的两个底面的面积是2πr2,
2πrh=2πr2,
因此,如果圆柱的高与它底面半径长度相等,那么圆柱体的侧面积等于两个底面积的和。此说法正确。
③把一个比的前项和后项都扩大3倍得到一个新的比,原来的比与新得到的比能组成比例。此说法正确。
④长方体、正方体和圆柱的体积都可以用“底面积×高”来计算。此说法正确。
答:说法正确的有3个。
故选:C。
【点评】此题考查的目的是理解掌握等底等高的圆柱与圆锥体积之间的关系及意义,圆柱的侧面积公式、圆的面积公式及意义,比例的意义及应用,长方体、正方体、圆柱体的体积公式及应用。
9.(2分)(2022秋 右玉县期末)淘气和妹妹手拉手一起从家出发去上学,途中淘气发现忘带作业本,于是他跑回家,找到作业本后向学校飞奔而去刚好在校门口追上了妹妹。如图正确描述淘气和妹妹上学路上情景的是( )
A. B.
C.
【考点】简单的行程问题.
【专题】数据分析观念;应用意识.
【答案】A
【分析】根据题意可知,妹妹没有停留一直走到学校,所以表示妹妹行走的图象是一条直线,淘气和妹妹一起去上学,所以他们一开始的图象是重合在一起的,途中淘气发现忘带作业本,于是他跑回家,拿好作业本,表示淘气行走的图象是一条折线,且在家中拿作业本这段时间形走的距离不变,然后马上向学校飞奔而去,刚好在校门口追上了妹妹。这时表示他们两人行走的图象交于一点,据此对照下面的图象进行选择即可。
【解答】解:由分析得:所以表示妹妹行走的图象是一条直线,表示淘气行走的图象,途中返回是折线,且在家中拿作业本这段时间形走的距离不变,然后马上向学校飞奔而去,刚好在校门口追上了妹妹。这时表示他们两人行走的图象交于一点。由此可知,图A描述的是淘气和妹妹上学路上的情景。
故选:A。
【点评】此题考查的目的是理解掌握复式折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
10.(2分)(2023春 漳州期末)小英、小红、小明三人赛跑,小明说:“我不是第一名,但是比小红快。”小明是第( )名。
A.1 B.2 C.3
【考点】逻辑推理.
【专题】压轴题;推理能力.
【答案】B
【分析】小明说:“我不是第一名,但是比小红快。”说明小明处在中间,即第二名,据此解答即可。
【解答】解:小明说:“我不是第一名,但是比小红快。”说明小明既不是第一名,也不是第三名,即第二名。
答:小明是第2名。
故选:B。
【点评】本题考查了简单的逻辑推理问题。
二.填空题(共7小题,满分14分,每小题2分)
11.(2分)(2022 椒江区)截至2022年5月,全国累计新冠疫苗接种人数达十二亿八千六百零四万九千人,这个数写作 1286049000 ,把这个数改写成用“亿”作单位,且精确到百分位约为 13 亿。
【考点】亿以上数的读写;亿以上数的改写与近似.
【专题】数感.
【答案】1286049000,13。
【分析】整数的写法:从高位到低位,一级一级地写,哪一个数位上一个单位也没有,就在那个数位上写0。
通过四舍五入法求整数的近似数,要对省略的尾数部分的最高位上的数进行四舍五入,若小于5则直接舍去,若大于或等于5,则向前一位进一,并加上“亿”。
【解答】解:截至2022年5月,全国累计新冠疫苗接种人数达十二亿八千六百零四万九千人,这个数写作:1286049000,把这个数改写成用“亿”作单位,且精确到百分位约为13亿。
故答案为:1286049000,13。
【点评】熟练掌握整数写法、整数的改写及近似数的求法,是解答此题的关键。
12.(2分)(2023春 龙华区期中) 6 ÷8== 75 %= 18 :24。
【考点】比与分数、除法的关系.
【专题】分数和百分数;数据分析观念.
【答案】6,75,18。
【分析】解答此题的关键是,根据分数的基本性质,分子、分母都乘6就是,根据比与分数的关系=18:24;根据分数与除法的关系,=3÷4,再根据商不变的性质,被除数、除数都乘2就是6÷8;=3÷4=0.75,把0.75的小数点向右移动两位,添上百分号就是75%,由此进行转化并填空。
【解答】解:6÷8==75%=18:24。
故答案为:6,75,18。
【点评】此题主要是考查除法、小数、分数、百分数、比之间的关系及转化,利用它们之间的关系和性质进行转化即可。
13.(4分)(2024秋 西固区期中)少年宫在图书馆西偏北30°200米处,则图书馆在少年宫( 东 偏 南 ) 30 °200米处。
【考点】根据方向和距离确定物体的位置.
【专题】综合题;空间观念.
【答案】东,南,30。
【分析】两个位置是相对的,分别以它们为观察中心时,看到对方的方向相反,角度和距离相等。
【解答】解:少年宫在图书馆西偏北30°200米处,则图书馆在少年宫东偏南30°200米处。
故答案为:东,南,30。
【点评】本题考查的是根据方向和距离确定物体位置的应用。
14.(2分)(2024秋 石狮市期末)在一次交通安全抽查中,通过某路口行人的头盔佩戴率达到90%。赵阳说:“这一时段通过这个路口的10个行人中,一定有9个行人佩戴头盔。”你同意这个说法吗?把你的想法写一写。我 不同意 (填“同意”或“不同意”),理由是: 90%的头盔佩戴率是一个统计结果,如果观察较多的行人,大约90%的人会佩戴头盔。如果任意选取其中10个行人,那么不一定是9个人佩戴头盔 。
【考点】百分率应用题.
【专题】综合填空题;数据分析观念.
【答案】不同意,90%的头盔佩戴率是一个统计结果,如果观察较多的行人,大约90%的人会佩戴头盔。如果任意选取其中10个行人,那么不一定是9个人佩戴头盔(答案不唯一)。
【分析】百分率表示一个数是另一个数的百分之几的数,通常用百分号(%)来表示;用百分数的形式来表示两个数的比值,据此解答。
【解答】解:我不同意,理由是:90%的头盔佩戴率是一个统计结果,如果观察较多的行人,大约90%的人会佩戴头盔。如果任意选取其中10个行人,那么不一定是9个人佩戴头盔(答案不唯一)。
故答案为:不同意,90%的头盔佩戴率是一个统计结果,如果观察较多的行人,大约90%的人会佩戴头盔。如果任意选取其中10个行人,那么不一定是9个人佩戴头盔(答案不唯一)。
【点评】此题考查了百分率的知识,要求学生掌握。
15.(1分)解比例的依据是 比例的基本性质 。
【考点】解比例.
【专题】比和比例;运算能力.
【答案】比例的基本性质。
【分析】根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个比例中的另外一个未知项。求比例中的未知项,叫做解比例,所以解比例的依据是比例的基本性质。
【解答】解:解比例的依据是比例的基本性质。
故答案为:比例的基本性质。
【点评】此题主要考查了解比例问题,要熟练掌握,注意比例的基本性质的应用。
16.(1分)如图所示正方形的边长为20cm,则阴影部分面积为 129 平方厘米。
【考点】圆与组合图形.
【专题】几何直观.
【答案】129。
【分析】根据图形的特点,边长为20厘米的正方形面积减去半径为20厘米的圆面积的是图中①、②的面积和;
边长为20厘米的正方形面积减去直径为20厘米的圆的面积,然后除以4等于图中①的面积;
然后用①、②的面积和减去①的面积,再乘2就是阴影部分的面积,据此列式解答。
【解答】解:如图:
20×20﹣3.14×202×
=400﹣314
=86(平方厘米)
[20×20﹣3.14×(20÷2)2]÷4
=[400﹣3.14×100]÷4
=[400﹣314]÷4
=86÷4
=21.5(平方厘米)
(86﹣21.5)×2
=64.5×2
=129(平方厘米)
答:阴影部分的面积是129平方厘米。
故答案为:129。
【点评】本题考查了圆与组合图形面积计算知识,解答这类问题,关键是观察分析图形是由哪几部分组成的,是求各部分的面积和、还是求各部分的面积差,再根据相应的面积公式解答即可。
17.(2分)(2023秋 滨江区期末)如图,按规律继续画下去,第8个图形共有 64 个■, 36 个□。
【考点】数与形结合的规律.
【专题】推理能力;模型思想.
【答案】64;36。
【分析】通过数形结合的规律解答此题。观察图形,可得出如下规律:第1个有:,1×1个■,3×3﹣1×1个□;第2个有:2×2个■,4×4﹣2×2个□;第3个有:3×3个■,5×5﹣3×3个□;第4个有:4×4个■,6×6﹣4×4个□;……
以此类推:第n个有:n×n个■,(n+2)×(n+2)﹣n×n个□。据此解答。
【解答】解:观察图形,可得出如下规律:
第1个有:,1×1个■,3×3﹣1×1个□;
第2个有:2×2个■,4×4﹣2×2个□;
第3个有:3×3个■,5×5﹣3×3个□;
第4个有:4×4个■,6×6﹣4×4个□;
……
以此类推:
第n个有:n×n个■,(n+2)×(n+2)﹣n×n个□;
第8个有:8×8=64个■,(8+2)×(8+2)﹣8×8=36个□。
答:第8个图形共有64个■,36个□。
故答案为:64;36。
【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力。
三.计算题(共1小题,满分18分,每小题18分)
18.(18分)(2023 庆城县)计算下面各题,能简算的要简算。
3600÷25÷4
0.6×3.3+×7.7﹣60% ÷[﹣(﹣0.25)]
【考点】整数、分数、小数、百分数四则混合运算;运算定律与简便运算;分数的四则混合运算.
【专题】运算能力.
【答案】36,0,6,。
【分析】(1)根据除法的性质简算;
(2)根据加法交换律和减法的性质简算;
(3)根据乘法分配律简算;
(4)先根据减法的性质简算,再算括号外的除法。
【解答】解:(1)3600÷25÷4
=3600÷(25×4)
=3600÷100
=36
(2)
=(+)﹣(+)
=1﹣1
=0
(3)0.6×3.3+×7.7﹣60%
=0.6×(3.3+7.7﹣1)
=0.6×10
=6
(4)÷[﹣(﹣0.25)]
=÷[+0.25﹣]
=÷[1﹣]
=÷
=
【点评】本题考查了四则混合运算,注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
四.操作题(共3小题,满分14分)
19.(6分)(2021 杭锦后旗)①三角形直角顶点用数对 (3,7) 表示。
②画出图中三角形绕点O顺时针旋转90°后的图形。
③把旋转后的图形按2:1放大。
【考点】数对与位置;作旋转一定角度后的图形;图形的放大与缩小.
【专题】几何直观;应用意识.
【答案】①(3,7);
②如图:
③如图:
【分析】①根据利用数对表示物体位置的方法,用数对表示物体的位置时,列数在前,行数在后。据此用数对表示出直角三角形直角顶点的位置。
②根据图形旋转的性质,图形旋转后,图形的形状和大小不变,只是图形的位置发生了变化。据此画出图中三角形绕点O顺时针旋转90°后的图形。
③根据图形放大的方法,下求出放大2倍后,三角形的底和高各是多少,据此画出放大后的三角形。据此解答。
【解答】解:①三角形直角顶点用数对(3,7)表示。
②将直角三角形ABO绕点O顺时针旋转90°。作图如下:
③放大后三角形的底是:2×2=4
放大后三角形的高是:3×2=6
作图如下:
故答案为:(3,7)。
【点评】此题考查的目的是理解掌握利用数对表示物体位置的方法及应用,图形旋转的性质、图形放大的方法及应用。
20.(6分)(2021春 榆阳区校级期中)把一个棱长为2cm的正方体的6个面展开(如图)。
(1)在展开图中标出剩下三个面的名称。
(2)这个正方体的棱长总和是 24 cm,表面积是 24 cm2,体积是 8 cm3。
【考点】正方体的展开图;长方体和正方体的表面积;长方体和正方体的体积.
【专题】空间观念;几何直观;应用意识.
【答案】(1);
(2)24,24,8。
【分析】(1)此图属于正方体展开图的“1﹣3﹣2”型,折成正方体后,第一行的左边一个正方形(标有“上”)与第二行的中间一个正方形相对;上行的第二个正方形(标有“前”)与第三行的正方形相对;第二行的第一个正方形(标有“左”)的正方形与本行的第三个正方形相对。根据“前﹣后、左﹣右、上﹣下”即可在图中标出剩下三个面的名称。
(2)正方体有12条相等的棱,每条棱的长度乘12,就是这个正方体的棱长总和;根据正方体的表面积计算公式“S=6a2”即可求出这个正方体的表面积;根据正方体的体积计算公式“V=a3”即可求出这个正方体的体积。
【解答】解:(1)
(2)2×12=24(cm)
2×2×6=24(cm2)
2×2×2=8(cm3)
答:这个正方体的棱长总和是24cm,表面积是24cm2,体积是8cm3。
故答案为:24,24,8。
【点评】此题考查的知识点:正方体展开图、正方体的特征、正方体表面积的计算、正方体体积的计算。
21.(2分)(2023春 福清市期中)在学习正方体的表面积时,我们观察过正方体的展开图。现在请画出一种正方体展开图,并标明6个面的序号。
【考点】正方体的展开图.
【专题】空间观念;几何直观.
【答案】(答案不唯一)。
【分析】画法不唯一。根据正方体展开图的11种特征,即可画出一种正方体展开图,并标明6个面的序号。
【解答】解:
(答案不唯一)。
【点评】此题是考查正方体展开图的认识。正方体展开图分四种类型,11种情况,要掌握每种情况的特征。每种情况,哪些面相对是有规律的,也要掌握。
五.解答题(共7小题,满分34分)
22.(3分)(2021春 邯郸期末)将4克糖放入51克水中,糖占水的,糖占糖水的。
【考点】部分占总数的几分之几.
【专题】分数和百分数;数据分析观念.
【答案】,。
【分析】利用糖的质量除以水的质量,利用糖加水求出糖水的质量,再利用糖的质量除以糖水的质量即可。
【解答】解:4÷51=
4÷(4+51)
=4÷55
=
答:糖占水的,糖占糖水的。
故答案为:,。
【点评】本题考查了一个数占另一个数的几分之几的解答方法。
23.(3分)小明读一本书,已经读了全书的,如果再读24页,则读过的页数与未读的页数的比是2:3。这本书有多少页?
【考点】比的应用.
【专题】比和比例.
【答案】160页。
【分析】读过的页数与未读的页数的比是2:3,则读过的页数占总页数的,24页对应的分率是(﹣),求总页数,用除法即可。
【解答】解:由读过的页数与未读的页数的比是2:3,
得,24÷(﹣)
=24÷
=160(页)
答:这本书有160页。
【点评】本题是一道有关比的应用、分数的混合运算的题目。
24.(3分)(2023秋 简阳市期末)动物运动会将要开幕,兔子家族要选拔一人去参加运动会,派谁去比较合适呢?请通过计算说明理由。
【考点】简单的行程问题.
【专题】应用题;数据分析观念.
【答案】黑兔子。
【分析】根据“速度=路程÷时间”,先求出白兔子和黑兔子的速度,进而比较它们的速度,选出速度快的兔子参加运动会。
【解答】解:白兔子:64.8÷8=8.1(米/秒)
黑兔子:136÷16=8.5(米/秒)
8.5>8.1
答:派黑兔子去比较合适。
【点评】此题主要考查路程、速度、时间三者的关系式:路程=速度×时间,速度=路程÷时间,时间=路程÷速度,灵活变形列式解决问题。
25.(3分)(2023秋 龙岩期中)实验小学四年级3个班学生去大熊猫馆参观,一班48人,二班45人,三班47人。大熊猫馆票价规定如下:
购票人数 1~50 51~100 101~150
票价(元/人) 25 20 18
四年级3个班学生购票最少要花多少元?
【考点】最优化问题.
【专题】应用题;应用意识.
【答案】2520元。
【分析】根据价格表可知,购票人数越多,票价越低,即3个班级应合起来一起买票。据此解答。
【解答】解:48+45+47=140(人)
140×18=2520(元)
答:四年级3个班学生购票最少要花2520元。
【点评】本题考查了最优化问题的应用。
26.(6分)(2024 天宁区)我国是一个水资源严重短缺的国家,节约用水是每个人都应该养成的好习惯.为鼓励居民合理用水,常州规定居民用水收费标准如表①。
表①
用水量 收费方式 备注
不超过15立方米 基本价 每户以3人为计算标准。如果每户人口超过3人的,每增加1人,月用水量增加5立方米。
超过15立方米 未超过的部分仍按基本价,超过的部分按调节价收费
王宇家共有3口人,今年四、五月的用水量和水费如表②。
表②
月份 用水量/立方米 水贵/元
四 15 56.55
五 17 65.93
(1)常州居民用水水费的基本价是 3.77 元/立方米,调节价是 4.69 元/立方米。
(2)王宇家六月份的用水量是20立方米,六月份的水费是多少元?
【考点】整数、小数复合应用题.
【专题】综合题;应用意识.
【答案】(1)3.77;4.69。(2)80元。
【分析】(1)根据题意,未超过15立方米时,水费按“基本价”收费,四月份用15立方米未超过15立方米,水费是56.55元,用56.55除以15求出“基本价”;五月份超过15立方米,超出17﹣15=2(立方米),用五月份水费的钱数﹣15立方米的水费钱数,求出超出部分的钱数,再除以超出2立方米即可求出“调节价”;(2)20立方米水分成两部分计算,用15立方米的水费钱数加上超出(20﹣15)立方米的钱数即可。
【解答】解:(1)56.55÷15=3.77(元/立方米)
(65.93﹣56.55)÷(17﹣15)
=9.38÷2
=4.69(元/立方米)
答:常州居民用水水费的基本价是3.77元/立方米,调节价是4.69元/立方米。
(2)56.55+(20﹣15)×4.69
=56.55+5×4.69
=56.55+23.45
=80(元)
答:六月份的水费是80元。
故答案为:3.77;4.69。
【点评】本题考查整数小数复合应用,熟练掌握单价×数量=总价,分段计费的计算方法是解答本题的关键。
27.(7分)教育部办公厅在印发的《关于加强中小学生手机管理工作的通知》中倡导:做好手机管理工作,保护学生视力,让学生在学校专心学习,防止沉迷网络和游戏.如图是阳光小学六年级200名学生使用手机情况统计图,请观察统计图并回答问题。
(1)手机用于查资料的有 45 人,并完成上面的条形统计图。
(2)本次调查活动中,手机用于玩游戏的人数占调查总人数的 25 %。
(3)根据以上调查结果,你想对同学们提出什么意见?
【考点】统计图表的填补;从统计图表中获取信息;扇形统计图.
【专题】数据分析观念;应用意识.
【答案】(1)45;
(2)25;
(3)减少玩手机游戏时间,保护视力。(答案不唯一)
【分析】(1)手机用于查资料的人数=调查总人数200×查资料的人数占总人数的百分率,然后补全条形统计图;
(2)手机用于玩游戏的人数占调查总人数的百分率=手机用于玩游戏的人数÷调查总人数×100%;
(3)建议减少玩手机游戏时间,保护视力。(答案不唯一)
【解答】解:(1)200×22.5%
=200×0.225
=45(人)
(2)50÷200×100%
=0.25×100%
=25%
答:手机用于玩游戏的人数占调查总人数的25%。
(3)建议减少玩手机游戏时间,保护视力。(答案不唯一)
故答案为:45;25。
【点评】本题关键是先读懂扇形统计图,找出各个量之间的关系,再把这一关系在条形统计图上表示出来。
28.(9分)(2022春 渑池县期中)一个圆柱形蓄水池从里面量底面直径是8m,深2.5m。
(1)这个蓄水池的占地面积约是多少?
(2)在蓄水池的内壁和底面抹上水泥,抹水泥部分的面积是多少?
(3)这个蓄水池最多能蓄水多少m3?
【考点】关于圆柱的应用题.
【专题】空间观念;应用意识.
【答案】(1)50.24平方米;
(2)113.04平方米;
(3)125.6立方米。
【分析】(1)根据圆的面积公式:S=πr2,把数据代入公式解答。
(2)因为水池无盖,所以抹水泥部分的面积是这个圆柱的一个底面的面积加上侧面积,根据圆的面积公式:S=πr2,圆柱的侧面积公式:S=πdh,把数据代入公式解答。
(3)根据圆柱的容积(体积)公式:V=Sh,把数据代入公式解答。
【解答】解:(1)3.14×(8÷2)2
=3.14×16
=50.24(平方米)
答:这个蓄水池的占地面积是50.24平方米。
(2)50.24+3.14×8×2.5
=50.24+62.8
=113.04(平方米)
答:抹水泥的面积是113.04平方米。
(3)50.24×2.5=125.6(立方米)
答:这个蓄水池最多能蓄水125.6立方米。
【点评】此题主要考查圆的面积公式、圆柱的侧面积公式、圆柱的体积公式在实际生活中的应用,关键是熟记公式。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
