专题12 二次函数的图象与性质(50 题)【最新中考模拟题】-2025学年中考数学满分冲刺(全国通用)(含答案+解析)
文档属性
| 名称 | 专题12 二次函数的图象与性质(50 题)【最新中考模拟题】-2025学年中考数学满分冲刺(全国通用)(含答案+解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 451.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-06 22:20:04 | ||
图片预览




文档简介
2025学年中考数学满分冲刺(全国通用)【最新中考模拟题】
专题12 二次函数的图象与性质(50 题)
一、选择题
1.(2025·邛崃模拟)某同学用描点法画二次函数的图象时,列出了下面的表格,请你根据获得的信息分析下列四个结论,其中正确的是( )
A.对称轴为
B.关于的一元二次方程只有一个根
C.当时,随的减小而减小
D.二次函数图象的顶点坐标为
2.(2025·旌阳模拟)如图,二次函数(为常数,)的图象与轴交于点,对称轴是直线,下面说法正确的个数是( )
(1);
(2);
(3)(为任意实数);
(4)若点和点都在抛物线上,则;
A.1个 B.2个 C.3个 D.4个
3.(2025·连州模拟)抛物线与轴相交的坐标为( )
A. B. C. D.
4.(2025·新兴模拟)二次函数与一次函数在同一平面直角坐标系中的大致图象可能是( )
A. B.
C. D.
5.(2025·株洲模拟)对于二次函数的图像性质,下列说法不正确的是( )
A.开口向上 B.过定点
C.有最小值 D.与轴一定有交点
6.(2025·梓潼模拟)如图,二次函数的图象经过点和点.给出下列结论:①;②;③当时,的值小于0.其中正确的是( )
A.①② B.①③ C.②③ D.①②③
7.(2025·平武模拟)如果将抛物线向右平移1个单位长度,再向下平移2个单位长度,那么所得的抛物线的解析式是( )
A. B. C. D.
8.(2025·凉州模拟)在平面直角坐标系中,若二次函数的图象如图所示,则以下结论中正确的是( )
A. B. C. D.
9.(2025·增城模拟)二次函数与反比例函数在同一直角坐标系中的图象可能是( )
A. B.
C. D.
10.(2025·黄埔模拟)抛物线中的的部分对应值如下表:
x … 0 1 3 4 …
y … 7 0 0 …
关于它的图象和性质,下列说法正确的是( )
A.图象开口向下
B.对称轴是直线
C.当时,y随x的增大而增大
D.图象与x轴的交点坐标为和
11.(2025·宁海模拟)二次函数的图象上有,两点.下列正确的选项是( )
A.当时, B.当时,
C.当时, D.当时,
12.(2025·浙江模拟) 已知二次函数 ,当 时,函数的最大值与最小值的和为 2,则 n 的取值范围是( )
A. B. C. D.
13.(2025·浙江二模)在平面直角坐标系中,点在抛物线上.设抛物线的对称轴为直线.若当时,都有,则的取值范围为( )
A. B. C. D.或
14.(2025·浙江模拟) 关于 x 的函数 ,,,当 时,,若 ,则
A. B. C. D.
15.(2025·金东二模) 将二次函数的图象先向下平移2个单位,再向右平移2个单位所得新函数表达式为( )
A. B.
C. D.
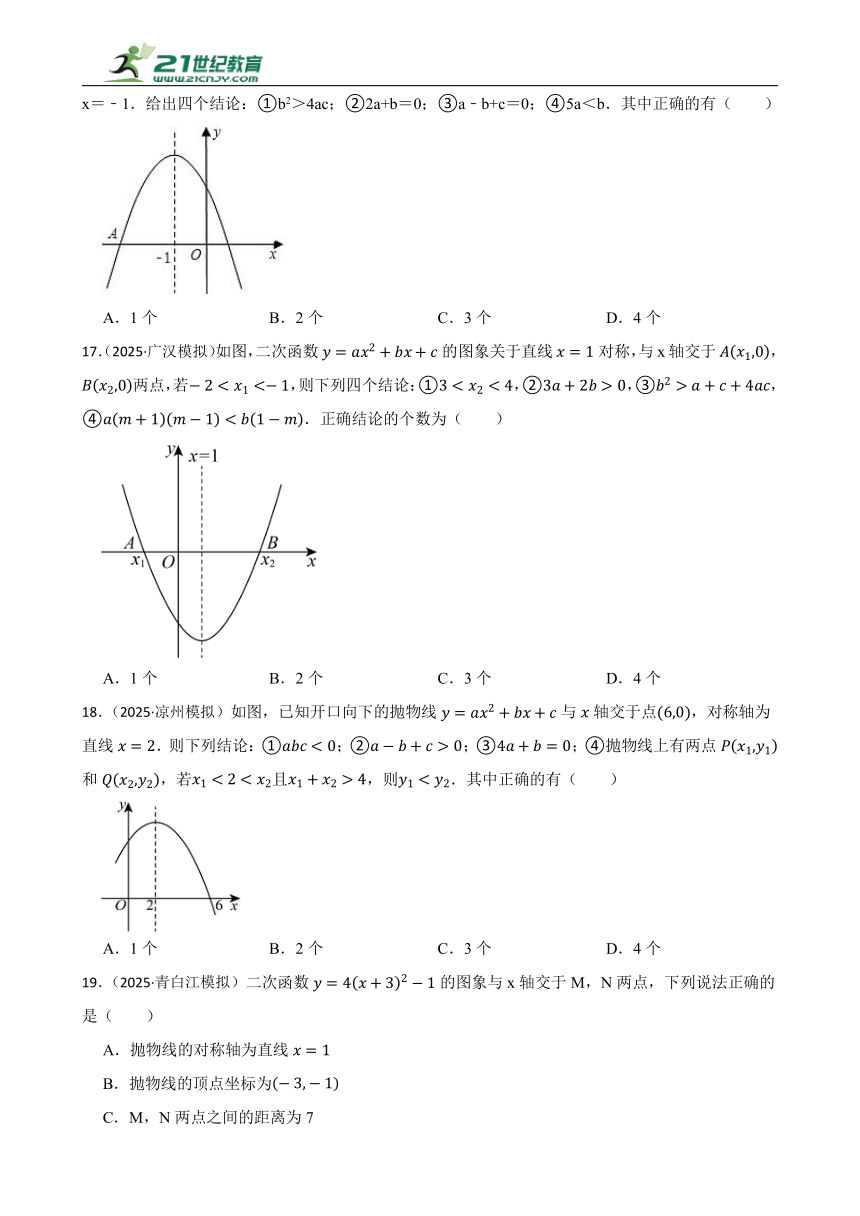
16.(2025·邻水模拟)如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为x=﹣1.给出四个结论:①b2>4ac;②2a+b=0;③a﹣b+c=0;④5a<b.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
17.(2025·广汉模拟)如图,二次函数的图象关于直线对称,与x轴交于,两点,若,则下列四个结论:①,②,③,④.正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
18.(2025·凉州模拟)如图,已知开口向下的抛物线与轴交于点,对称轴为直线.则下列结论:①;②;③;④抛物线上有两点和,若且,则.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
19.(2025·青白江模拟)二次函数的图象与x轴交于M,N两点,下列说法正确的是( )
A.抛物线的对称轴为直线
B.抛物线的顶点坐标为
C.M,N两点之间的距离为7
D.当时,y的值随x值的增大而增大
20.(2025·连州模拟)抛物线如图所示,抛物线与轴交于点,顶点坐标为,下列结论:①;②;③对于任意实数,都有;④当时,.其中正确的个数是( )
A.1 B.2 C.3 D.4
21.(2025·祁阳模拟)已知抛物线,下列结论错误的是( )
A.抛物线开口向上 B.抛物线的对称轴为直线
C.抛物线的顶点坐标为 D.当时,y随x的增大而增大
22.(2025·湖南模拟)在平面直角坐标系中,抛物线 (t为常数)与直线有两个不同的交点,且交点的横坐标都满足,则t的取值范围为( )
A. B. C. D.
23.(2025·萧山模拟)已知二次函数的图象经过点,,若,则下列可能成立的是( )
A.当时, B.当时,
C.当时, D.当时,
24.(2025·凉州模拟)如图,已知二次函数的图象与x轴交于点,顶点为,则下列结论:①;②;③;④若,则.其中正确的有( )
A.①②③ B.①②④ C.①③④ D.②③④
25.(2025·白云模拟)已知二次函数()与轴交于、两点,与轴交点的纵坐标是,且,则以下结论中不正确的是( )
A.
B.
C.抛物线的顶点坐标为
D.若,则或
26.(2025·萧山模拟)已知二次函数的图象经过点,若,则下列可能成立的是( )
A.当时, B.当时,
C.当时, D.当时,
27.(2025·雅安模拟)如图,抛物线,与轴交于点,其对称轴为直线,结合图象给出下列结论:
①; ②;
③; ④对于任意实数.
其中正确的结论有( )
A.1 B.2 C.3 D.4
28.(2025·平武模拟)已知二次函数(a ,b,c为常数)的图象如图所示,则一次函数与反比例函数 在同一平面直角坐标系内的大致图象是( )
A. B.
C. D.
29.(2025·苍溪模拟)如图,已知顶点为的抛物线过点,给出下列结论:①;②对于任意的实数m,均有;③;④若,则;⑤;⑥已知点均在抛物线上,若,,则.其中正确的个数有( )
A.2个 B.3个 C.4个 D.5个
30.(2025·广东模拟)已知抛物线与轴有两个交点为,下列命题错误的个数有( )
①②③④
A. B. C. D.
31.(2025·隆昌模拟)在直角坐标系中,点在二次函数的图象上,对于,当,,时,依次对应的函数值,,中最大的是( )
A. B.
C. D.或()
32.(2024九下·沛县模拟)在平面直角坐标系中,将二次函数的图象向右平移2个单位长度,再向下平移1个单位长度,所得拋物线对应的函数表达式为( )
A. B. C. D.
33.(2025·杭州模拟) 已知二次函数 (a,c 是常数,) 的图象经过点 , , ( )
A.若 , , 则 B.若 , , 则
C.若 , , 则 D.若 , , 则
34.(2025·锦江模拟)已知抛物线的图象及对称轴如图所示,则下列结论错误的是( )
A. B. C. D.
35.(2025·西湖模拟)已知二次函数(是常数,)的图象经过点,,下列说法正确的是( )
A.若,,则 B.若,,则
C.若,,则 D.若,,则
36.(2025·仁寿模拟)如图,抛物线的顶点A的坐标为,与x轴的一个交点的横坐标位于0和之间,则以下结论:①;②;③若抛物线经过点,,则;④若关于x的一元二次方程有实数根,则.其中正确的个数为( )
A.4 B.3 C.2 D.1
37.(2025·祁阳模拟)对于平面直角坐标系 中的抛物线G 和抛物线G 外的点P ,给出如下定义:在抛物线G 上若存在两点M,N,使为等腰直角三角形且, 则称抛物线G为点P的T型线,点P为抛物线G的T型点.若 是抛物线的T型点,则n的取值范围是( )
A. B. C. D.n ≥
38.(2025·长宁模拟)定义:在平面直角坐标系中,横坐标与纵坐标相等的点称为“完美点”.设抛物线与y轴相交于点M,将抛物线L关于y轴对称,且向上平移1个单位后得到抛物线.若抛物线L上的完美点也在抛物线上,则下列结论中:①抛物线L上的完美点是或;②a的值是或;③存在某条定直线l,与抛物线交于点A,使得平行于x轴.正确的是( )
A.①② B.①③ C.②③ D.①②③
39.(2025·叙州模拟)如图,抛物线的图像交轴负半轴于点,交轴正半轴于点,交轴负半轴于点,点为抛物线的顶点,连结、、,且.以下结论:①点坐标为;②;③;④在内存在唯一一点,使得的值最小,若的最小值为,则.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
40.(2025·北川模拟)如图,抛物线与x轴交于两点,且给出下列结论:①;②;③当时,y 随x 的增大而减小;④的值是一个定值;⑤b的取值范围是.其中正确的个数是( )
A.5 B.4 C.3 D.2
二、填空题
41.(2025·冷水滩模拟)我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点、、、分别是“果圆”与坐标轴的交点,抛物线的解析式为,为半圆的直径,则这个“果圆”被轴截得的弦的长为 .
42.(2025·武冈模拟)已知抛物线与x轴交于A,B两点,对称轴与抛物线交于点C,与x轴交于点D,的半径为1,G为上一动点,P为的中点,则的最大值为 .
43.(2025·陇南模拟)将抛物线先向上平移5个单位长度,再向右平移1个单位长度后,得到的抛物线解析式是 .
44.(2025·普陀二模)已知点(m,n)在直线y=x+b(b为常数)上,若mn的最小值为-1,则b= 。
45.(2025·高坪模拟)已知关于x的一元二次方程的两个根分别是1和-3,若二次函数与x轴有两个交点,其中一个交点坐标是(4,0),则另一个交点坐标是 .
46.(2025·高坪模拟)已知关于的二次函数的图象经过点,,,且,对于以下结论:①;②;③对于自变量的任意一个取值,都有;④在中存在一个实数,使得,其中结论正确的是 .(只填写序号)
47.(2025·眉山模拟)将抛物线在轴下方的部分沿轴翻折,图象其余部分不变,得到一个新图象如图所示.
(1)当直线过点时,则的值为 ;
(2)当直线与新图象有四个公共点时,则的取值范围是 .
48.(2025·濠江模拟)若抛物线(是常数)与轴没有交点,则的取值范围是 .
49.(2025·椒江二模) 如图1,在Rt△ABC中,∠ACB=90°,点E是斜边AB上一个动点.过点E作EF⊥AB,垂足为E,交边AC(或边CB)于点F,连接CE,设AE=x,△CEF的面积为y,则y与x之间的函数图象如图2,已知,则tanA= .
50.(2025·香洲模拟)抛物线过两点,将抛物线L向左或向右平移后得到抛物线M,设抛物线M的顶点为C.若是以为斜边的直角三角形,则点C的坐标为 .
答案解析部分
1.D
2.B
3.B
4.D
5.D
6.D
7.A
8.C
9.C
10.C
11.C
12.C
13.C
解:由条件可知:开口向上,离对称轴的距离越近,其对应的函数值也就越小,
∵点A(-2,y1),B(2,y2),C(m,y3)在抛物线
y=ax2+bx+3(a>0)上,且y1>y3>y2,
∴|h+2|>|m-h|>|h-2|,
由条件可得1<|m-h|<2,
∴
解得:1≤h≤3;
故答案为:C.
根据“开口向上,离对称轴的距离越近,其对应的函数值也就越小”可知:|h+2|>|m-h|>|h-2|,然后可得,进而问题可求解.
14.C
15.D
解:将y=-x2的图象先向下平移2个单位长度,再向右平移2个单位长度,则所得二次函数的表达式为:y=-(x-2)2-2.
故答案为:D.
根据抛物线的平移规律:上加下减,左加右减解答即可.
16.B
17.B
18.C
19.B
20.C
21.D
解:抛物线中,a>0,抛物线开口向上,因此A选项正确,不符合题意;
由解析式得,对称轴为直线,因此B选项正确,不符合题意;
由解析式得,当时,y取最小值,最小值为1,所以抛物线的顶点坐标为,因此C选项正确,不符合题意;
因为抛物线开口向上,对称轴为直线,因此当时,y随x的增大而减小,因此D选项错误,符合题意.
故答案为:D.
根据抛物线解析式可得a=1>0,据此判断A;根据抛物线的解析式可得对称轴为直线x=2,顶点坐标为(2,1),据此判断B、C;根据开口方向以及对称轴可判断D.
22.D
23.B
解:、∵二次函数的图象经过点,,
∴,,
∵,
∴,
∴,原选项错误,不符合题意;
、∵,
∴,
∴当时,可能成立,原选项正确,符合题意;
、∵,
∴,即,
若若时,则,原选项可能不成立,不符合题意;
、∵,
∴,
∴,
若时,则,原选项可能不成立,不符合题意;
故选:.
由二次函数图象上点的坐标特征可把点的坐标分别代入解析式得到,,再根据,依次对各选项进行判断即可.
24.B
25.D
26.B
解:
把A(-2,m),B(5,n)代入y=ax2+bx+c中得m=4a-2b+c,n=25a+5b+c,
∵m<n,
∴4a-2b+c<25a+5b+c,
∴3a+b>0,
∴A选项不符合题意;
当a<0时,b-a>-4a>0,a+b>-2a>0,
∴C、D选项不符合题意;
当a>0时,2a+b>-a,
又∵-a<0,
∴2a+b=0是可能的.
∴B选项符合题意.
故答案为:B.
先把点A、B的坐标分别代入解析式得到m=4a-2b+c,n=25a+5b+c,然后利用m<n得到4a-2b+c<25a+5b+c,则3a+b>0,然后依次对各选项进行判断.
27.C
解: ∵对称轴为,
∴,即,
∴;
故①错误,
由图象可知当时,,
∴,
故②正确;
∵抛物线,与轴交于点,其对称轴为直线,
∴抛物线与轴的另一个交点为,
∴当时,,
故选项③正确;
∵抛物线抛物线开口向上,其对称轴为直线,
∴当时,函数有最小值,
∴对于任意实数.
∴对于任意实数n,
故选项④正确,
综上所述正确的有:②③④.
故选:C.
观察图象二次函数的对称轴可得到a、b的关系式,可对①作出判断;利用x=-2时y<0,可对②作出判断;利用二次函数的对称性,可知当x=1时y=0,可对③作出判断;利用二次函数的最值,可对④作出判断;综上所述,可得到正确结论的个数.
28.B
29.B
30.B
31.A
32.B
解:将二次函数y=(x+1)2+3的图象向右平移2个单位长度,再向下平移1个单位长度,所得拋物线对应的函数表达式为y=(x+1-2)2+3-1,即y=(x-1)2+2.
故答案为:B.
根据“左加右减,上加下减”的平移规则进行解答.
33.A
解:二次函数 化为顶点式为
∴该二次函数的对称轴为直线x =1,
当a>0时,二次函数图象开口向上,在对称轴右侧y随x的增大而增大,
若t > 2, 则点( 和 都在对称轴x=1右侧, 且t若t<1时, t+1<2, 则点( 和 都在对称轴x =1左侧,y随x的增大而小,t当1≤t≤2时, 点( 在对称轴左侧,点(t+1,y2)在对称轴右侧,此时无法直接比较y1与y2大小. 当a<0时,二次函数图象开口向下,在对称轴右侧y随x的增大而减小,
若t>2, 则点( 和 都在对称轴x=1右侧,且t1> y2,
若t<1时, t+1<2, 则点( 和 都在对称轴x =1左侧,y随x的增大而增大, t当1≤t≤2时, 点( )在对称轴左侧,点(t+1,y2)在对称轴右侧,此时无法直接比较y1与y2大小. 综上, 当a>0, t>2时,
故答案为:A .
先将二次函数化为顶点式来确定对称轴,再根据a的政府判断函数的开口向上,然后结合点(t,y1)与 的大小关系.
34.C
35.A
解:∵二次函数的图象经过点,,
∴
,
A、若,,
∴,,
∴此选项符合题意;
B、若,,则,正负无法确定,
∴不一定成立,
∴此选项不符合题意;
C、若,,则,
∴,
∴此选项不符合题意;
D、若,,则,正负无法确定,
∴ 不一定成立,
∴此选项不符合题意.
故答案为:A.
根据二次函数图象上点的坐标特征,可求得,再结合各选项即可判断求解.
36.C
37.C
38.D
39.D
40.B
解:①∵抛物线与x轴交于两点,
∴抛物线的对称轴为直线,
∵,
∴,
∴,
∴,
∴,故①错误;
②由函数图象可知抛物线与y轴交于点,代入解析式得,
把代入解析式,得,
∴,
∴,故②正确;
③∵抛物线的开口向下,
∴当时,y随x 的增大而减小,
又∵,
∴当时,y 随x 的增大而减小,故③正确;
④把代入,得,
∵,
∴,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∴,即的值是一个定值,故④正确;
⑤∵,
∴,
∴,
∵,
∴,
解得:,故⑤正确;
综上所述,正确个数有4个,
故答案为:B.
根据抛物线的对称轴可求出,即可判断①;根据抛物线与y轴的交点求出,与x轴的交点求出,利用完全平方公式可判断②;由抛物线的对称轴,利用二次函数的增减性可判断③;把代入解析式,得,再根据,得,由,得,,于是求得,可判断④;由以及得到关于b的不等式组,解不等式组求得b的取值范围可判断⑤.
41.
42.3
43.
44.±2
解:将点(m,n)代入y=x+b中得,
n=m+b,
则mn=m(m+b)=m2+mb,
∵ mn的最小值为-1,
∴m>0,且当时,mn取最小值,
则,
解得:b=±2;
故答案为:±2.
将点(m,n)代入y=x+b中得关于m,n的等式,再根据二次函数的性质,抛物线开口向上,存在最小值,利用二次函数顶点公式求最小值,即可得出关于b的方程,求解即可.
45.( 6,0)
46.①③④
47.;
48.
49.
解:过点C作CD⊥AB于点D,如图,
观察图象可发现:当点E运动到点D时,C,F两点重合,△CEF不存在,当点E运动到点B时,E,F两点重合,△CEF不存在,
则对应函数图象上第二个和第三个零点,
设m=3k,n=7k(k>0),
由函数图象对称的性质可得第二个和第三个零点的值分别为6k,8k,
则AD=6k,BD=2k,
∵∠A+∠ACD=∠A+∠B=90°,
∴∠ACD=∠B,
∵∠ADC=∠BDC=90°,
∴△ACD∽△CBD,
∴,
即CD2=12k2,
∴,
∴
故答案为:.
过点C作CD⊥AB于点D,观察图象可发现:①当点E运动到点D时,C,F两点重合,②当点E运动到点B时,E,F两点重合,△CEF不存在;设m=3k,n=7k(k>0),由函数图象对称的性质,证明△ACD∽△CBD,从而推出正确答案.
50.或
专题12 二次函数的图象与性质(50 题)
一、选择题
1.(2025·邛崃模拟)某同学用描点法画二次函数的图象时,列出了下面的表格,请你根据获得的信息分析下列四个结论,其中正确的是( )
A.对称轴为
B.关于的一元二次方程只有一个根
C.当时,随的减小而减小
D.二次函数图象的顶点坐标为
2.(2025·旌阳模拟)如图,二次函数(为常数,)的图象与轴交于点,对称轴是直线,下面说法正确的个数是( )
(1);
(2);
(3)(为任意实数);
(4)若点和点都在抛物线上,则;
A.1个 B.2个 C.3个 D.4个
3.(2025·连州模拟)抛物线与轴相交的坐标为( )
A. B. C. D.
4.(2025·新兴模拟)二次函数与一次函数在同一平面直角坐标系中的大致图象可能是( )
A. B.
C. D.
5.(2025·株洲模拟)对于二次函数的图像性质,下列说法不正确的是( )
A.开口向上 B.过定点
C.有最小值 D.与轴一定有交点
6.(2025·梓潼模拟)如图,二次函数的图象经过点和点.给出下列结论:①;②;③当时,的值小于0.其中正确的是( )
A.①② B.①③ C.②③ D.①②③
7.(2025·平武模拟)如果将抛物线向右平移1个单位长度,再向下平移2个单位长度,那么所得的抛物线的解析式是( )
A. B. C. D.
8.(2025·凉州模拟)在平面直角坐标系中,若二次函数的图象如图所示,则以下结论中正确的是( )
A. B. C. D.
9.(2025·增城模拟)二次函数与反比例函数在同一直角坐标系中的图象可能是( )
A. B.
C. D.
10.(2025·黄埔模拟)抛物线中的的部分对应值如下表:
x … 0 1 3 4 …
y … 7 0 0 …
关于它的图象和性质,下列说法正确的是( )
A.图象开口向下
B.对称轴是直线
C.当时,y随x的增大而增大
D.图象与x轴的交点坐标为和
11.(2025·宁海模拟)二次函数的图象上有,两点.下列正确的选项是( )
A.当时, B.当时,
C.当时, D.当时,
12.(2025·浙江模拟) 已知二次函数 ,当 时,函数的最大值与最小值的和为 2,则 n 的取值范围是( )
A. B. C. D.
13.(2025·浙江二模)在平面直角坐标系中,点在抛物线上.设抛物线的对称轴为直线.若当时,都有,则的取值范围为( )
A. B. C. D.或
14.(2025·浙江模拟) 关于 x 的函数 ,,,当 时,,若 ,则
A. B. C. D.
15.(2025·金东二模) 将二次函数的图象先向下平移2个单位,再向右平移2个单位所得新函数表达式为( )
A. B.
C. D.
16.(2025·邻水模拟)如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为x=﹣1.给出四个结论:①b2>4ac;②2a+b=0;③a﹣b+c=0;④5a<b.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
17.(2025·广汉模拟)如图,二次函数的图象关于直线对称,与x轴交于,两点,若,则下列四个结论:①,②,③,④.正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
18.(2025·凉州模拟)如图,已知开口向下的抛物线与轴交于点,对称轴为直线.则下列结论:①;②;③;④抛物线上有两点和,若且,则.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
19.(2025·青白江模拟)二次函数的图象与x轴交于M,N两点,下列说法正确的是( )
A.抛物线的对称轴为直线
B.抛物线的顶点坐标为
C.M,N两点之间的距离为7
D.当时,y的值随x值的增大而增大
20.(2025·连州模拟)抛物线如图所示,抛物线与轴交于点,顶点坐标为,下列结论:①;②;③对于任意实数,都有;④当时,.其中正确的个数是( )
A.1 B.2 C.3 D.4
21.(2025·祁阳模拟)已知抛物线,下列结论错误的是( )
A.抛物线开口向上 B.抛物线的对称轴为直线
C.抛物线的顶点坐标为 D.当时,y随x的增大而增大
22.(2025·湖南模拟)在平面直角坐标系中,抛物线 (t为常数)与直线有两个不同的交点,且交点的横坐标都满足,则t的取值范围为( )
A. B. C. D.
23.(2025·萧山模拟)已知二次函数的图象经过点,,若,则下列可能成立的是( )
A.当时, B.当时,
C.当时, D.当时,
24.(2025·凉州模拟)如图,已知二次函数的图象与x轴交于点,顶点为,则下列结论:①;②;③;④若,则.其中正确的有( )
A.①②③ B.①②④ C.①③④ D.②③④
25.(2025·白云模拟)已知二次函数()与轴交于、两点,与轴交点的纵坐标是,且,则以下结论中不正确的是( )
A.
B.
C.抛物线的顶点坐标为
D.若,则或
26.(2025·萧山模拟)已知二次函数的图象经过点,若,则下列可能成立的是( )
A.当时, B.当时,
C.当时, D.当时,
27.(2025·雅安模拟)如图,抛物线,与轴交于点,其对称轴为直线,结合图象给出下列结论:
①; ②;
③; ④对于任意实数.
其中正确的结论有( )
A.1 B.2 C.3 D.4
28.(2025·平武模拟)已知二次函数(a ,b,c为常数)的图象如图所示,则一次函数与反比例函数 在同一平面直角坐标系内的大致图象是( )
A. B.
C. D.
29.(2025·苍溪模拟)如图,已知顶点为的抛物线过点,给出下列结论:①;②对于任意的实数m,均有;③;④若,则;⑤;⑥已知点均在抛物线上,若,,则.其中正确的个数有( )
A.2个 B.3个 C.4个 D.5个
30.(2025·广东模拟)已知抛物线与轴有两个交点为,下列命题错误的个数有( )
①②③④
A. B. C. D.
31.(2025·隆昌模拟)在直角坐标系中,点在二次函数的图象上,对于,当,,时,依次对应的函数值,,中最大的是( )
A. B.
C. D.或()
32.(2024九下·沛县模拟)在平面直角坐标系中,将二次函数的图象向右平移2个单位长度,再向下平移1个单位长度,所得拋物线对应的函数表达式为( )
A. B. C. D.
33.(2025·杭州模拟) 已知二次函数 (a,c 是常数,) 的图象经过点 , , ( )
A.若 , , 则 B.若 , , 则
C.若 , , 则 D.若 , , 则
34.(2025·锦江模拟)已知抛物线的图象及对称轴如图所示,则下列结论错误的是( )
A. B. C. D.
35.(2025·西湖模拟)已知二次函数(是常数,)的图象经过点,,下列说法正确的是( )
A.若,,则 B.若,,则
C.若,,则 D.若,,则
36.(2025·仁寿模拟)如图,抛物线的顶点A的坐标为,与x轴的一个交点的横坐标位于0和之间,则以下结论:①;②;③若抛物线经过点,,则;④若关于x的一元二次方程有实数根,则.其中正确的个数为( )
A.4 B.3 C.2 D.1
37.(2025·祁阳模拟)对于平面直角坐标系 中的抛物线G 和抛物线G 外的点P ,给出如下定义:在抛物线G 上若存在两点M,N,使为等腰直角三角形且, 则称抛物线G为点P的T型线,点P为抛物线G的T型点.若 是抛物线的T型点,则n的取值范围是( )
A. B. C. D.n ≥
38.(2025·长宁模拟)定义:在平面直角坐标系中,横坐标与纵坐标相等的点称为“完美点”.设抛物线与y轴相交于点M,将抛物线L关于y轴对称,且向上平移1个单位后得到抛物线.若抛物线L上的完美点也在抛物线上,则下列结论中:①抛物线L上的完美点是或;②a的值是或;③存在某条定直线l,与抛物线交于点A,使得平行于x轴.正确的是( )
A.①② B.①③ C.②③ D.①②③
39.(2025·叙州模拟)如图,抛物线的图像交轴负半轴于点,交轴正半轴于点,交轴负半轴于点,点为抛物线的顶点,连结、、,且.以下结论:①点坐标为;②;③;④在内存在唯一一点,使得的值最小,若的最小值为,则.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
40.(2025·北川模拟)如图,抛物线与x轴交于两点,且给出下列结论:①;②;③当时,y 随x 的增大而减小;④的值是一个定值;⑤b的取值范围是.其中正确的个数是( )
A.5 B.4 C.3 D.2
二、填空题
41.(2025·冷水滩模拟)我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点、、、分别是“果圆”与坐标轴的交点,抛物线的解析式为,为半圆的直径,则这个“果圆”被轴截得的弦的长为 .
42.(2025·武冈模拟)已知抛物线与x轴交于A,B两点,对称轴与抛物线交于点C,与x轴交于点D,的半径为1,G为上一动点,P为的中点,则的最大值为 .
43.(2025·陇南模拟)将抛物线先向上平移5个单位长度,再向右平移1个单位长度后,得到的抛物线解析式是 .
44.(2025·普陀二模)已知点(m,n)在直线y=x+b(b为常数)上,若mn的最小值为-1,则b= 。
45.(2025·高坪模拟)已知关于x的一元二次方程的两个根分别是1和-3,若二次函数与x轴有两个交点,其中一个交点坐标是(4,0),则另一个交点坐标是 .
46.(2025·高坪模拟)已知关于的二次函数的图象经过点,,,且,对于以下结论:①;②;③对于自变量的任意一个取值,都有;④在中存在一个实数,使得,其中结论正确的是 .(只填写序号)
47.(2025·眉山模拟)将抛物线在轴下方的部分沿轴翻折,图象其余部分不变,得到一个新图象如图所示.
(1)当直线过点时,则的值为 ;
(2)当直线与新图象有四个公共点时,则的取值范围是 .
48.(2025·濠江模拟)若抛物线(是常数)与轴没有交点,则的取值范围是 .
49.(2025·椒江二模) 如图1,在Rt△ABC中,∠ACB=90°,点E是斜边AB上一个动点.过点E作EF⊥AB,垂足为E,交边AC(或边CB)于点F,连接CE,设AE=x,△CEF的面积为y,则y与x之间的函数图象如图2,已知,则tanA= .
50.(2025·香洲模拟)抛物线过两点,将抛物线L向左或向右平移后得到抛物线M,设抛物线M的顶点为C.若是以为斜边的直角三角形,则点C的坐标为 .
答案解析部分
1.D
2.B
3.B
4.D
5.D
6.D
7.A
8.C
9.C
10.C
11.C
12.C
13.C
解:由条件可知:开口向上,离对称轴的距离越近,其对应的函数值也就越小,
∵点A(-2,y1),B(2,y2),C(m,y3)在抛物线
y=ax2+bx+3(a>0)上,且y1>y3>y2,
∴|h+2|>|m-h|>|h-2|,
由条件可得1<|m-h|<2,
∴
解得:1≤h≤3;
故答案为:C.
根据“开口向上,离对称轴的距离越近,其对应的函数值也就越小”可知:|h+2|>|m-h|>|h-2|,然后可得,进而问题可求解.
14.C
15.D
解:将y=-x2的图象先向下平移2个单位长度,再向右平移2个单位长度,则所得二次函数的表达式为:y=-(x-2)2-2.
故答案为:D.
根据抛物线的平移规律:上加下减,左加右减解答即可.
16.B
17.B
18.C
19.B
20.C
21.D
解:抛物线中,a>0,抛物线开口向上,因此A选项正确,不符合题意;
由解析式得,对称轴为直线,因此B选项正确,不符合题意;
由解析式得,当时,y取最小值,最小值为1,所以抛物线的顶点坐标为,因此C选项正确,不符合题意;
因为抛物线开口向上,对称轴为直线,因此当时,y随x的增大而减小,因此D选项错误,符合题意.
故答案为:D.
根据抛物线解析式可得a=1>0,据此判断A;根据抛物线的解析式可得对称轴为直线x=2,顶点坐标为(2,1),据此判断B、C;根据开口方向以及对称轴可判断D.
22.D
23.B
解:、∵二次函数的图象经过点,,
∴,,
∵,
∴,
∴,原选项错误,不符合题意;
、∵,
∴,
∴当时,可能成立,原选项正确,符合题意;
、∵,
∴,即,
若若时,则,原选项可能不成立,不符合题意;
、∵,
∴,
∴,
若时,则,原选项可能不成立,不符合题意;
故选:.
由二次函数图象上点的坐标特征可把点的坐标分别代入解析式得到,,再根据,依次对各选项进行判断即可.
24.B
25.D
26.B
解:
把A(-2,m),B(5,n)代入y=ax2+bx+c中得m=4a-2b+c,n=25a+5b+c,
∵m<n,
∴4a-2b+c<25a+5b+c,
∴3a+b>0,
∴A选项不符合题意;
当a<0时,b-a>-4a>0,a+b>-2a>0,
∴C、D选项不符合题意;
当a>0时,2a+b>-a,
又∵-a<0,
∴2a+b=0是可能的.
∴B选项符合题意.
故答案为:B.
先把点A、B的坐标分别代入解析式得到m=4a-2b+c,n=25a+5b+c,然后利用m<n得到4a-2b+c<25a+5b+c,则3a+b>0,然后依次对各选项进行判断.
27.C
解: ∵对称轴为,
∴,即,
∴;
故①错误,
由图象可知当时,,
∴,
故②正确;
∵抛物线,与轴交于点,其对称轴为直线,
∴抛物线与轴的另一个交点为,
∴当时,,
故选项③正确;
∵抛物线抛物线开口向上,其对称轴为直线,
∴当时,函数有最小值,
∴对于任意实数.
∴对于任意实数n,
故选项④正确,
综上所述正确的有:②③④.
故选:C.
观察图象二次函数的对称轴可得到a、b的关系式,可对①作出判断;利用x=-2时y<0,可对②作出判断;利用二次函数的对称性,可知当x=1时y=0,可对③作出判断;利用二次函数的最值,可对④作出判断;综上所述,可得到正确结论的个数.
28.B
29.B
30.B
31.A
32.B
解:将二次函数y=(x+1)2+3的图象向右平移2个单位长度,再向下平移1个单位长度,所得拋物线对应的函数表达式为y=(x+1-2)2+3-1,即y=(x-1)2+2.
故答案为:B.
根据“左加右减,上加下减”的平移规则进行解答.
33.A
解:二次函数 化为顶点式为
∴该二次函数的对称轴为直线x =1,
当a>0时,二次函数图象开口向上,在对称轴右侧y随x的增大而增大,
若t > 2, 则点( 和 都在对称轴x=1右侧, 且t
若t>2, 则点( 和 都在对称轴x=1右侧,且t1> y2,
若t<1时, t+1<2, 则点( 和 都在对称轴x =1左侧,y随x的增大而增大, t
故答案为:A .
先将二次函数化为顶点式来确定对称轴,再根据a的政府判断函数的开口向上,然后结合点(t,y1)与 的大小关系.
34.C
35.A
解:∵二次函数的图象经过点,,
∴
,
A、若,,
∴,,
∴此选项符合题意;
B、若,,则,正负无法确定,
∴不一定成立,
∴此选项不符合题意;
C、若,,则,
∴,
∴此选项不符合题意;
D、若,,则,正负无法确定,
∴ 不一定成立,
∴此选项不符合题意.
故答案为:A.
根据二次函数图象上点的坐标特征,可求得,再结合各选项即可判断求解.
36.C
37.C
38.D
39.D
40.B
解:①∵抛物线与x轴交于两点,
∴抛物线的对称轴为直线,
∵,
∴,
∴,
∴,
∴,故①错误;
②由函数图象可知抛物线与y轴交于点,代入解析式得,
把代入解析式,得,
∴,
∴,故②正确;
③∵抛物线的开口向下,
∴当时,y随x 的增大而减小,
又∵,
∴当时,y 随x 的增大而减小,故③正确;
④把代入,得,
∵,
∴,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∴,即的值是一个定值,故④正确;
⑤∵,
∴,
∴,
∵,
∴,
解得:,故⑤正确;
综上所述,正确个数有4个,
故答案为:B.
根据抛物线的对称轴可求出,即可判断①;根据抛物线与y轴的交点求出,与x轴的交点求出,利用完全平方公式可判断②;由抛物线的对称轴,利用二次函数的增减性可判断③;把代入解析式,得,再根据,得,由,得,,于是求得,可判断④;由以及得到关于b的不等式组,解不等式组求得b的取值范围可判断⑤.
41.
42.3
43.
44.±2
解:将点(m,n)代入y=x+b中得,
n=m+b,
则mn=m(m+b)=m2+mb,
∵ mn的最小值为-1,
∴m>0,且当时,mn取最小值,
则,
解得:b=±2;
故答案为:±2.
将点(m,n)代入y=x+b中得关于m,n的等式,再根据二次函数的性质,抛物线开口向上,存在最小值,利用二次函数顶点公式求最小值,即可得出关于b的方程,求解即可.
45.( 6,0)
46.①③④
47.;
48.
49.
解:过点C作CD⊥AB于点D,如图,
观察图象可发现:当点E运动到点D时,C,F两点重合,△CEF不存在,当点E运动到点B时,E,F两点重合,△CEF不存在,
则对应函数图象上第二个和第三个零点,
设m=3k,n=7k(k>0),
由函数图象对称的性质可得第二个和第三个零点的值分别为6k,8k,
则AD=6k,BD=2k,
∵∠A+∠ACD=∠A+∠B=90°,
∴∠ACD=∠B,
∵∠ADC=∠BDC=90°,
∴△ACD∽△CBD,
∴,
即CD2=12k2,
∴,
∴
故答案为:.
过点C作CD⊥AB于点D,观察图象可发现:①当点E运动到点D时,C,F两点重合,②当点E运动到点B时,E,F两点重合,△CEF不存在;设m=3k,n=7k(k>0),由函数图象对称的性质,证明△ACD∽△CBD,从而推出正确答案.
50.或
同课章节目录
