专题20 多边形与平行四边形(50 题)【最新中考模拟题】-2025学年中考数学满分冲刺(全国通用)(含答案+解析)
文档属性
| 名称 | 专题20 多边形与平行四边形(50 题)【最新中考模拟题】-2025学年中考数学满分冲刺(全国通用)(含答案+解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-06 22:25:00 | ||
图片预览



文档简介
2025学年中考数学满分冲刺(全国通用)【最新中考模拟题】
专题20 多边形与平行四边形(50 题)
一、选择题
1.(2025·织金模拟)如图,在平行四边形中,,E,F分别是的中点,连接,则( )
A.2 B.3 C.8 D.无法确定
2.(2025·武冈模拟)在中,的角平分线交于点,点分为4和5两部分,则的周长为( )
A.24 B.26 C.28 D.26或28
3.(2025·深圳模拟)如图,某条楼梯及栏杆可以看作三角形与平行四边形构成,若,则该楼梯的坡角的值为( )
A. B. C. D.
4.(2025·衡阳模拟)如图,分别与相切于A、B两点,连接,若,则的度数为( )
A. B. C. D.
5.(2025·玉环模拟)如图,一束太阳光线平行照射在放置于地面的正六边形上,若,则的度数为( )
A. B. C. D.
6.(2024九下·邹平模拟)如图,在平行四边形中,BE平分∠ABC交DC于点E.若,则∠DEB的大小为( )
A.130° B.125° C.120° D.115°
7.(2025·连州模拟)已知正边形的一个外角为,则边形的内角和是( )
A. B. C. D.
8.(2025·双流模拟)如图,四边形是平行四边形,,若对角线的长为,的长为,则边的长为( )
A.8 B.6 C.5 D.4
9.(2024·仪征模拟)若一个凸多边形的内角和为720°,则这个多边形的边数为
A.4 B.5 C.6 D.7
10.(2025·广东模拟)如图,在四个相同的正方形网格中,分别作一个顶点均在格点上的平行四边形ABCD,其中边CD上的高最小的是
A. B.
C. D.
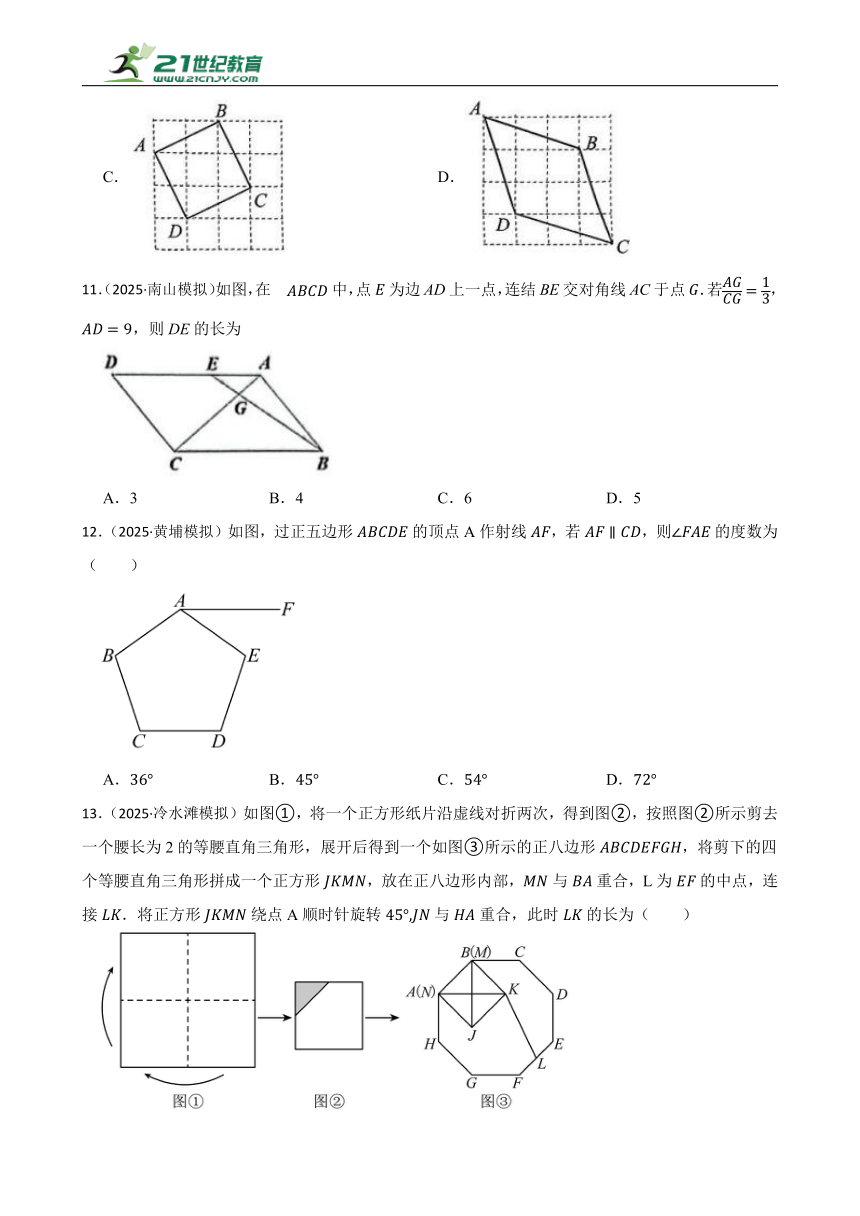
11.(2025·南山模拟)如图,在中,点为边AD上一点,连结BE交对角线AC于点.若,,则DE的长为
A.3 B.4 C.6 D.5
12.(2025·黄埔模拟)如图,过正五边形的顶点A作射线,若,则的度数为( )
A. B. C. D.
13.(2025·冷水滩模拟)如图①,将一个正方形纸片沿虚线对折两次,得到图②,按照图②所示剪去一个腰长为2的等腰直角三角形,展开后得到一个如图③所示的正八边形,将剪下的四个等腰直角三角形拼成一个正方形,放在正八边形内部,与重合,L为的中点,连接.将正方形绕点A顺时针旋转与重合,此时的长为( )
A.3 B. C. D.
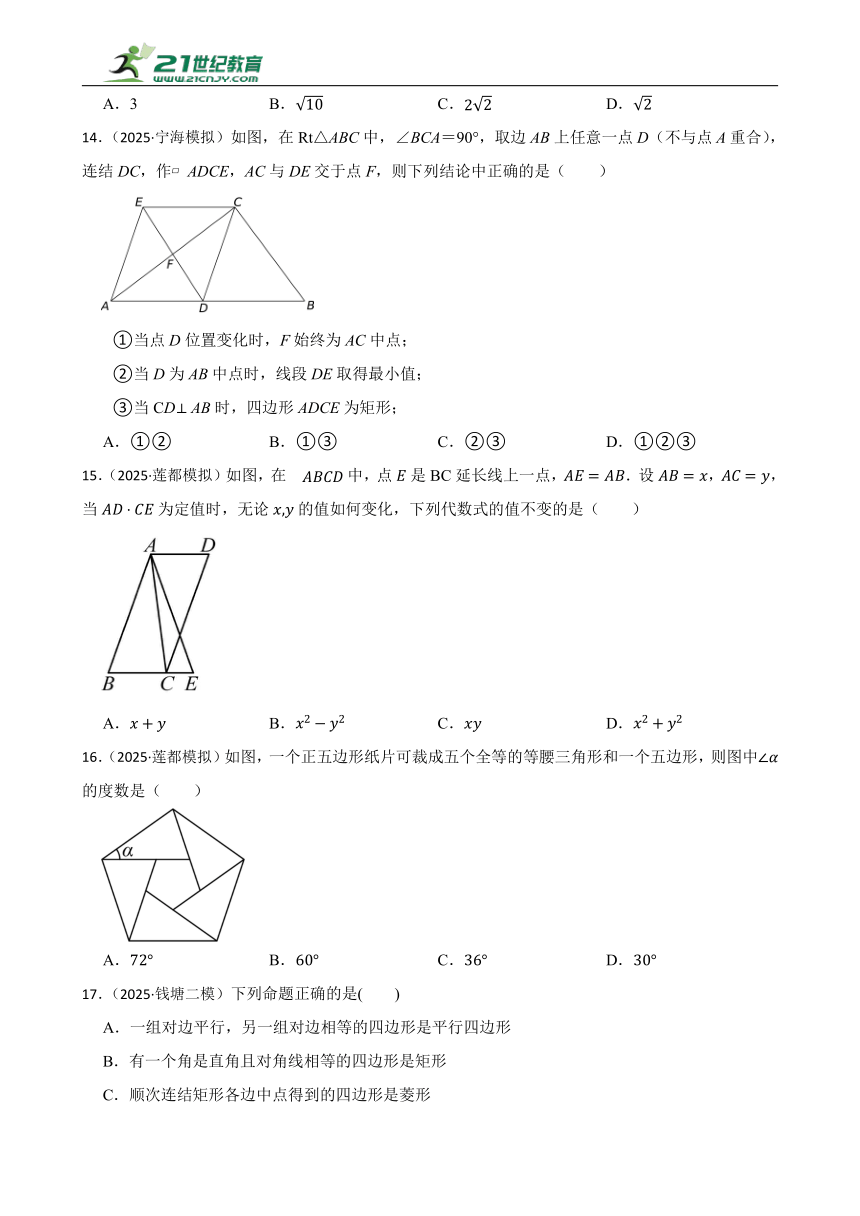
14.(2025·宁海模拟)如图,在Rt△ABC中,∠BCA=90°,取边AB上任意一点D(不与点A重合),连结DC,作 ADCE,AC与DE交于点F,则下列结论中正确的是( )
①当点D位置变化时,F始终为AC中点;
②当D为AB中点时,线段DE取得最小值;
③当CD AB时,四边形ADCE为矩形;
A.①② B.①③ C.②③ D.①②③
15.(2025·莲都模拟)如图,在中,点是BC延长线上一点,.设,,当为定值时,无论的值如何变化,下列代数式的值不变的是( )
A. B. C. D.
16.(2025·莲都模拟)如图,一个正五边形纸片可裁成五个全等的等腰三角形和一个五边形,则图中的度数是( )
A. B. C. D.
17.(2025·钱塘二模)下列命题正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.有一个角是直角且对角线相等的四边形是矩形
C.顺次连结矩形各边中点得到的四边形是菱形
D.对角线互相垂直且相等的四边形是正方形
18.(2025·诸暨二模) 如图,在平行四边形ABCD中,的顶点E,F分别在边AB,AD上,满足,,,,在CE上取一点M,满足,则( )
A.1 B. C. D.2
19.(2025·深圳模拟)如图,菱形中,,垂足为,点在线段上,过点作,,则的值为( )
A. B. C.1 D.
20.(2025·成都模拟)如图,已知平行四边形的顶点,,点B在x轴正半轴上,按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边于点D,E;②分别以点D,E为圆心,大于的长为半径作弧,两弧在内交于点F;③作射线,交边于点G,则点G的坐标为( )
A. B. C. D.
21.(2025·黄岩二模)如图,的对角线相交于点,点是AB的中点,连结OE.若,则的度数为( )
A. B. C. D.
22.(2025·凉州模拟)如图,在中,对角线交于,已知,,,那么到的距离为( )
A. B. C. D.
23.(2025·肇庆模拟)如图,已知在矩形中,是边的中点,与垂直,交直线于点,连接,则下列四个结论中:①;②;③;④.正确的有( )
A.①②③④ B.①②④ C.①③④ D.②③④
24.(2025·邻水模拟)如图,在平行四边形中(),直线经过其对角线的交点O,且分别交、于点M、N,交、的延长线于点E、F,下列结论:①;②;③;④,其中正确的是( )
A.①② B.②③ C.②④ D.③④
25.(2025·仁寿模拟)如图,在中,,以点D为圆心作弧,交于点M、N,分别以点M、N为圆心,大于为半径作弧,两弧交于点F,过点D作直线交于点E,若,则的周长是( )
A.16 B.14 C.12 D.10
26.(2025·广汉模拟)如图,中,以点B为圆心,适当长为半径作弧,分别交,于点E,F,分别以点E和点F为圆心,大于的长为半径作弧,两弧在内交于点O,作射线交于点G,交的延长线于点H,若,,的长为( )
A.4 B. C.5 D.
27.(2025·香洲模拟)如图,点P在平行四边形的对角线上,过点P作,.已知,,,则四边形的面积是( )
A.4 B.5 C.6 D.7
28.(2025·顺庆模拟)如图,反比例函数的图象经过对角线的交点,轴于,,则的值为( )
A.12 B.6 C.4 D.3
29.(2025·莲都模拟)如图,一个正五边形纸片可裁成五个全等的等腰三角形和一个五边形,则图中的度数是( )
A. B. C. D.
30.(2025·婺城模拟)如图,在中,对角线AC,BD交于点,点为BC中点,于点,已知.当x,y发生变化时,下列代数式值不变的是( )
A. B. C. D.
31.(2024九下·永州模拟)如图,的对角线相交于点O,的平分线与边相交于点P,E是的中点,若,则的长为( )
A.1 B. C. D.2
32.(2025·澄海模拟)如图,在平行四边形中,,,,点E是边上的动点,连接,,过点A作于点F.设,,则y与x之间的函数解析式为(不考虑自变量x的取值范围)( )
A. B. C. D.
33.(2025·新兴模拟)如图,在中,是的平分线,延长交的延长线于点.若,,则的长为( )
A.12 B.15 C.18 D.21
34.(2025·惠城模拟)如图是凸透镜成像示意图,是蜡烛通过凸透镜所成的虚像.已知蜡烛的高为,蜡烛离凸透镜的水平距离为,该凸透镜的焦距为,,则像的高为( )
A. B. C. D.
35.(2025·龙华模拟)如图,在四个相同的正方形网格中,分别作一个顶点均在格点上的平行四边形,其中边上的高最小的是( )
A. B.
C. D.
36.(2025·金华模拟)如图,在平行四边形中,的顶点,分别在边,上,满足,,,,在上一取点,满足,则( )
A.1 B. C. D.2
37.(2024九下·莱芜模拟)如图,在平行四边形中,是锐角,于点为的中点,连接,若,则的长是( )
A.6 B.8 C. D.
38.(2025·龙港模拟)如图,在中,分别是,的中点,是对角线上一点(点不与端点重合),过点作交于点,交于点.连结,,若已知的面积,则一定能求出( )
A.的面积 B.的面积 C.的面积 D.的面积
39.(2025·南山模拟)如图,在平面直角坐标系中,点的坐标为,点的坐标为,以OA、OC为边作矩形OABC;动点E,F分别从点O,B同时出发,以每秒1个单位长度的速度沿OA,BC向终点A,C移动;当移动时间为8秒时,的值( )
A.30 B. C.60 D.120
二、填空题
40.(2023·东坡模拟)如图,四边形是平行四边形,以点B为圆心,的长为半径作弧交于E,分别以点C,E为圆心,大于的长为半径作弧,两弧交于点P,作射线交的延长线于点F,,则 .
41.(2025·浙江二模)如图,在□ABCD中,点E是CD的中点,△CEF的面积为2,则∠ABE的面积为 .
42.(2025·黄埔模拟)如图,在平行四边形中,为上一点,且,与相交于点,,则 .
43.(2025·义乌模拟)如图1,在平行四边形中,,.点、分别是线段、上的点,连结、、.将和分别沿、翻折,使点的对应点和点的对应点都落在对角线上,连结、.
(1)如图2,若,则的值为 .
(2)若为钝角,延长交射线于点且,则的值为 .
44.(2025·澧县模拟)如图,在中,,作交的延长线于点,若是的中线,,则四边形的周长为 .
45.(2025·定海模拟)如图,在中,,于点,若,则 .
46.(2025·浙江模拟) 如图,菱形 ABCD中,点 E,F 分别是AB,CD上的点,已知 DF=3BE=6,DE=BF=2,则对角线 BD 的长为 .
47.(2025·瑞安二模) 如图,在 ABCD中,E是对角线BD上一点,过点E作FG//AB,分别交BC,AD于点F,G,将四边形ABFG沿FG翻折,得到四边形A'B'FG,点B'恰好落在BD上. 若,,,则的面积为 .
48.(2025·祁阳模拟)如图,在中,,D、E分别为上一点,,,与交于点P,则 度.
49.(2025·祁阳模拟)如图,平行四边形中,点是对角线的中点,点在边上,连接,取的中点,连接并延长交于点.若,,则线段的长是 .
50.(2025·旺苍模拟)如图,在平行四边形中,以为圆心,长为半径画弧交于点,分别以点,为圆心,大于的长为半径画弧,两弧交于点,连接并延长交于点,连接交于点,过点作于点.若,,则 .
答案解析部分
1.B
2.D
3.C
解:四边形是平行四边形,,
,
,
,
.
故选:C.
根据平行四边形的性质可得,再根据三角形内角和定理即可求出答案.
4.B
解:∵分别与相切于A、B两点,
∴;
∵,
∴;
故答案为:B.
由切线的性质可得,再由四边形内角和定理即可求解.
5.D
解:延长交于点H,如图,
∵六边形是正六边形,
∴,
又∵,
∴,
∴,
又∵,
∴;
故选:D.
根据正六边形得到,然后利用三角形内角和求出的度数,最后根据平行线的性质得出.
6.C
7.D
8.D
9.C
设这个多边形的边数为n,由多边形的内角和是720°,根据多边形的内角和定理得(n-2)180°=720°.解得n=6.故答案为:C.
设这个多边形的边数为n,根据多边形的内角和定理得到(n﹣2)×180°=720°,然后解方程即可.
10.A
解:A:平行四边形面积为:
,则CD边上的高为
B:平行四边形面积为:
,则CD边上的高为
C:该平行四边形为正方形
,则CD边上的高为
D:平行四边形面积为:
,则CD边上的高为
故答案为:A
先求出平行四边形面积,再根据勾股定理求出CD长,再根据面积求出CD边上的高,比较大小即可求出答案.
11.C
解:∵四边形ABCD是平行四边形,AD=8
∴AD∥BC,AD=BC=9
∴△AGE∽△CGB
∴
∵
∴
∵CB=9
∴AE=3
∴DE=AD-AE=6
故答案为:C
根据平行四边形性质可得AD∥BC,AD=BC=9,再根据相似三角形判定定理可得△AGE∽△CGB,则,根据题意可得AE=3,再根据边之间的关系即可求出答案.
12.A
13.B
14.B
15.B
16.C
17.C
解:A、一组对边平行,另一组对边相等的四边形可能是平行四边形也可能是等腰梯形,故原命题错误,不符合题意;
B、有一个角是直角且对角线互相平分的四边形是矩形,故原命题错误,不符合题意;
C、顺次连接矩形各边中点得到的四边形是菱形,正确,符合题意;
D、对角线互相垂直且相等的平行四边形是正方形,故原命题错误,不符合题意.
故答案为:C.
利用平行四边形、矩形、菱形及正方形的判定方法分别判断后即可确定正确的选项.
18.D
19.D
解:∵菱形中,,垂足为,
∴,,
∴,,
∵点在线段上,过点作,
∴,四边形是平行四边形,
∴,,
∴,
∵,
∴,
∴,整理得:,
解得:或(不合题意舍弃).
故选:D.
根据菱形性质可得,,再根据等腰直角三角形的性质以及勾股定理可得、,过点作,根据平行四边形判定定理可得四边形是平行四边形,则,,再根据边之间的关系可得,,再根据三角形面积化简即可求出答案.
20.A
21.A
解:∵四边形ABCD是平行四边形,
∴OA=OC,及O为AC的中点,
∵ E是AB的中点,
∴OE是△ABC的中位线,
∴OE∥BC,
∴∠AOE=∠ACB=88°;
故答案为:A.
根据平行四边形的性质及中点的定义判定OE为三角形中位线,根据中位线定理即可得解.
22.B
23.A
24.B
25.C
26.B
27.B
28.B
29.C
解:
如图,五个全等的等腰三角形拼成内外两个正五边形,
∴∠ABD==108°,∠DBC=∠BAC,
∵∠α+∠ACB+∠BAC=180°,
∴∠ACB=∠BAC=180°-108°=72°,
∴∠α=180°-∠ACB-∠BAC=180°-72°-72°=36°,
故答案为:C.
根据题目描述,五个完全相同的等腰三角形组合构成了内外两个正五边形,通过计算正五边形的内角可知∠ABD为108度,运用三角形内角和为180度的性质,可以推导出∠ACB和∠BAC均为72度(180°-108°),最终即可求得∠α的具体数.
30.C
解:连接OE,如图所示:
由条件可知AB=CD=5,,AO=CO,AD=BC=y,AD//BC,,
∵E为BC的中点,O为BD的中点,
∴OE//CD,,
∴△OPE∽△CPD,
∴
∴,,
∵DE⊥AC,
∴∠OPE=∠EPC=∠CPD=∠OPD=90°,
根据勾股定理得:,
PC2+PD2=52,,
∴,PC2+PD2=25,,
∴,,
∴,
∴x2+y2=5PC2+5PD2=5×25=125,
∴x2+y2为定值.
故答案为:C.
连接OE,根据平行四边形的性质得出AB=CD=5,,AO=CO,AD=BC=y,AD//BC,根据中位线性质得出OE//CD,,证明△OPE∽△CPD,得出,根据勾股定理,即可得出答案.
31.A
32.C
33.C
34.C
35.A
36.D
37.D
38.B
39.D
解:当移动时间为8秒时,OE=8,BF=8
∵四边形OABC是矩形
∴OA=BC,OA∥BC,∠AOC=90°
∵点A的坐标为(18,0)
∴OA=18
∴BC=18
∴AE=10,CF=10
∴AE=CF
∵OA∥BC
∴四边形AECF是平行四边形
∵点C的坐标为(0,6)
∴OC=6
在Rt△COE中,由勾股定理可得
∴CE=AE
∴四边形AECF是菱形
连接AC,EF,则AC⊥EF
∴
∴=2×10×6=120
故答案为:D
当移动时间为8秒时,OE=8,BF=8,根据矩形性质可得OA=BC,OA∥BC,∠AOC=90°,根据点的坐标可得OA=18,再根据边之间的关系可得AE=CF,再根据平行四边形判定定理可得四边形AECF是平行四边形,根据勾股定理可得CE,再根据菱形判定定理可得四边形AECF是菱形,连接AC,EF,则AC⊥EF,再根据菱形面积即可求出答案.
40.
41.12
42.24
43.(1);
44.
45.
46.
47.
解:如图,连接AA',
∵四边形ABCD是平行四边形,
∴AD//BC
∵FG//AB,
∴四边形ABFG是平行四边形,
∴AB=GF,AG=BF,
由折叠可得:四边形A'GFB'是平行四边形,
∴A'B'=GF,A'B'//GF//AB,
∴AB=GF=A'B',
∵由对折可得:AB=A'B',FB=FB',AG=A'G,BE=B'E,
∴
∴HG=AG=A'G,
∴A'在以G为圆心,AH为直径的圆上,
∴∠AA'H=90°,
∵AD//BC,
∴△DGE∽△BFE,
∴,
∴,而AG+ DG= AD= 28,
∴AG=8,DG=20,
∴HG=AG=A'G=8,
∴AH=16,DH=12,
∵A'H = DH,
∴A'H=DH=12,
∴,
∴
∵AB//A'B',AB=A'B',
∴四边形ABB'A'为平行四边形,
∴AA'//DB',
∴△AA'H∽△DB'H,
∴
∴,
故答案为:.
如图,连接AA',由折叠可得:四边形A'GFB'是平行四边形,可得A'B'=GF,A'B'//GF//AB,AB=GF=A'B',,证明,HG=AG=A'G,可得A'在以G为圆心,AH为直径的圆上,∠AA'H=90°,证明出△DGE∽△BFE,可得AG=8,DG=20,,,再进一步利用相似三角形的性质,即可得出结论.
48.135
49.
50.
专题20 多边形与平行四边形(50 题)
一、选择题
1.(2025·织金模拟)如图,在平行四边形中,,E,F分别是的中点,连接,则( )
A.2 B.3 C.8 D.无法确定
2.(2025·武冈模拟)在中,的角平分线交于点,点分为4和5两部分,则的周长为( )
A.24 B.26 C.28 D.26或28
3.(2025·深圳模拟)如图,某条楼梯及栏杆可以看作三角形与平行四边形构成,若,则该楼梯的坡角的值为( )
A. B. C. D.
4.(2025·衡阳模拟)如图,分别与相切于A、B两点,连接,若,则的度数为( )
A. B. C. D.
5.(2025·玉环模拟)如图,一束太阳光线平行照射在放置于地面的正六边形上,若,则的度数为( )
A. B. C. D.
6.(2024九下·邹平模拟)如图,在平行四边形中,BE平分∠ABC交DC于点E.若,则∠DEB的大小为( )
A.130° B.125° C.120° D.115°
7.(2025·连州模拟)已知正边形的一个外角为,则边形的内角和是( )
A. B. C. D.
8.(2025·双流模拟)如图,四边形是平行四边形,,若对角线的长为,的长为,则边的长为( )
A.8 B.6 C.5 D.4
9.(2024·仪征模拟)若一个凸多边形的内角和为720°,则这个多边形的边数为
A.4 B.5 C.6 D.7
10.(2025·广东模拟)如图,在四个相同的正方形网格中,分别作一个顶点均在格点上的平行四边形ABCD,其中边CD上的高最小的是
A. B.
C. D.
11.(2025·南山模拟)如图,在中,点为边AD上一点,连结BE交对角线AC于点.若,,则DE的长为
A.3 B.4 C.6 D.5
12.(2025·黄埔模拟)如图,过正五边形的顶点A作射线,若,则的度数为( )
A. B. C. D.
13.(2025·冷水滩模拟)如图①,将一个正方形纸片沿虚线对折两次,得到图②,按照图②所示剪去一个腰长为2的等腰直角三角形,展开后得到一个如图③所示的正八边形,将剪下的四个等腰直角三角形拼成一个正方形,放在正八边形内部,与重合,L为的中点,连接.将正方形绕点A顺时针旋转与重合,此时的长为( )
A.3 B. C. D.
14.(2025·宁海模拟)如图,在Rt△ABC中,∠BCA=90°,取边AB上任意一点D(不与点A重合),连结DC,作 ADCE,AC与DE交于点F,则下列结论中正确的是( )
①当点D位置变化时,F始终为AC中点;
②当D为AB中点时,线段DE取得最小值;
③当CD AB时,四边形ADCE为矩形;
A.①② B.①③ C.②③ D.①②③
15.(2025·莲都模拟)如图,在中,点是BC延长线上一点,.设,,当为定值时,无论的值如何变化,下列代数式的值不变的是( )
A. B. C. D.
16.(2025·莲都模拟)如图,一个正五边形纸片可裁成五个全等的等腰三角形和一个五边形,则图中的度数是( )
A. B. C. D.
17.(2025·钱塘二模)下列命题正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.有一个角是直角且对角线相等的四边形是矩形
C.顺次连结矩形各边中点得到的四边形是菱形
D.对角线互相垂直且相等的四边形是正方形
18.(2025·诸暨二模) 如图,在平行四边形ABCD中,的顶点E,F分别在边AB,AD上,满足,,,,在CE上取一点M,满足,则( )
A.1 B. C. D.2
19.(2025·深圳模拟)如图,菱形中,,垂足为,点在线段上,过点作,,则的值为( )
A. B. C.1 D.
20.(2025·成都模拟)如图,已知平行四边形的顶点,,点B在x轴正半轴上,按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边于点D,E;②分别以点D,E为圆心,大于的长为半径作弧,两弧在内交于点F;③作射线,交边于点G,则点G的坐标为( )
A. B. C. D.
21.(2025·黄岩二模)如图,的对角线相交于点,点是AB的中点,连结OE.若,则的度数为( )
A. B. C. D.
22.(2025·凉州模拟)如图,在中,对角线交于,已知,,,那么到的距离为( )
A. B. C. D.
23.(2025·肇庆模拟)如图,已知在矩形中,是边的中点,与垂直,交直线于点,连接,则下列四个结论中:①;②;③;④.正确的有( )
A.①②③④ B.①②④ C.①③④ D.②③④
24.(2025·邻水模拟)如图,在平行四边形中(),直线经过其对角线的交点O,且分别交、于点M、N,交、的延长线于点E、F,下列结论:①;②;③;④,其中正确的是( )
A.①② B.②③ C.②④ D.③④
25.(2025·仁寿模拟)如图,在中,,以点D为圆心作弧,交于点M、N,分别以点M、N为圆心,大于为半径作弧,两弧交于点F,过点D作直线交于点E,若,则的周长是( )
A.16 B.14 C.12 D.10
26.(2025·广汉模拟)如图,中,以点B为圆心,适当长为半径作弧,分别交,于点E,F,分别以点E和点F为圆心,大于的长为半径作弧,两弧在内交于点O,作射线交于点G,交的延长线于点H,若,,的长为( )
A.4 B. C.5 D.
27.(2025·香洲模拟)如图,点P在平行四边形的对角线上,过点P作,.已知,,,则四边形的面积是( )
A.4 B.5 C.6 D.7
28.(2025·顺庆模拟)如图,反比例函数的图象经过对角线的交点,轴于,,则的值为( )
A.12 B.6 C.4 D.3
29.(2025·莲都模拟)如图,一个正五边形纸片可裁成五个全等的等腰三角形和一个五边形,则图中的度数是( )
A. B. C. D.
30.(2025·婺城模拟)如图,在中,对角线AC,BD交于点,点为BC中点,于点,已知.当x,y发生变化时,下列代数式值不变的是( )
A. B. C. D.
31.(2024九下·永州模拟)如图,的对角线相交于点O,的平分线与边相交于点P,E是的中点,若,则的长为( )
A.1 B. C. D.2
32.(2025·澄海模拟)如图,在平行四边形中,,,,点E是边上的动点,连接,,过点A作于点F.设,,则y与x之间的函数解析式为(不考虑自变量x的取值范围)( )
A. B. C. D.
33.(2025·新兴模拟)如图,在中,是的平分线,延长交的延长线于点.若,,则的长为( )
A.12 B.15 C.18 D.21
34.(2025·惠城模拟)如图是凸透镜成像示意图,是蜡烛通过凸透镜所成的虚像.已知蜡烛的高为,蜡烛离凸透镜的水平距离为,该凸透镜的焦距为,,则像的高为( )
A. B. C. D.
35.(2025·龙华模拟)如图,在四个相同的正方形网格中,分别作一个顶点均在格点上的平行四边形,其中边上的高最小的是( )
A. B.
C. D.
36.(2025·金华模拟)如图,在平行四边形中,的顶点,分别在边,上,满足,,,,在上一取点,满足,则( )
A.1 B. C. D.2
37.(2024九下·莱芜模拟)如图,在平行四边形中,是锐角,于点为的中点,连接,若,则的长是( )
A.6 B.8 C. D.
38.(2025·龙港模拟)如图,在中,分别是,的中点,是对角线上一点(点不与端点重合),过点作交于点,交于点.连结,,若已知的面积,则一定能求出( )
A.的面积 B.的面积 C.的面积 D.的面积
39.(2025·南山模拟)如图,在平面直角坐标系中,点的坐标为,点的坐标为,以OA、OC为边作矩形OABC;动点E,F分别从点O,B同时出发,以每秒1个单位长度的速度沿OA,BC向终点A,C移动;当移动时间为8秒时,的值( )
A.30 B. C.60 D.120
二、填空题
40.(2023·东坡模拟)如图,四边形是平行四边形,以点B为圆心,的长为半径作弧交于E,分别以点C,E为圆心,大于的长为半径作弧,两弧交于点P,作射线交的延长线于点F,,则 .
41.(2025·浙江二模)如图,在□ABCD中,点E是CD的中点,△CEF的面积为2,则∠ABE的面积为 .
42.(2025·黄埔模拟)如图,在平行四边形中,为上一点,且,与相交于点,,则 .
43.(2025·义乌模拟)如图1,在平行四边形中,,.点、分别是线段、上的点,连结、、.将和分别沿、翻折,使点的对应点和点的对应点都落在对角线上,连结、.
(1)如图2,若,则的值为 .
(2)若为钝角,延长交射线于点且,则的值为 .
44.(2025·澧县模拟)如图,在中,,作交的延长线于点,若是的中线,,则四边形的周长为 .
45.(2025·定海模拟)如图,在中,,于点,若,则 .
46.(2025·浙江模拟) 如图,菱形 ABCD中,点 E,F 分别是AB,CD上的点,已知 DF=3BE=6,DE=BF=2,则对角线 BD 的长为 .
47.(2025·瑞安二模) 如图,在 ABCD中,E是对角线BD上一点,过点E作FG//AB,分别交BC,AD于点F,G,将四边形ABFG沿FG翻折,得到四边形A'B'FG,点B'恰好落在BD上. 若,,,则的面积为 .
48.(2025·祁阳模拟)如图,在中,,D、E分别为上一点,,,与交于点P,则 度.
49.(2025·祁阳模拟)如图,平行四边形中,点是对角线的中点,点在边上,连接,取的中点,连接并延长交于点.若,,则线段的长是 .
50.(2025·旺苍模拟)如图,在平行四边形中,以为圆心,长为半径画弧交于点,分别以点,为圆心,大于的长为半径画弧,两弧交于点,连接并延长交于点,连接交于点,过点作于点.若,,则 .
答案解析部分
1.B
2.D
3.C
解:四边形是平行四边形,,
,
,
,
.
故选:C.
根据平行四边形的性质可得,再根据三角形内角和定理即可求出答案.
4.B
解:∵分别与相切于A、B两点,
∴;
∵,
∴;
故答案为:B.
由切线的性质可得,再由四边形内角和定理即可求解.
5.D
解:延长交于点H,如图,
∵六边形是正六边形,
∴,
又∵,
∴,
∴,
又∵,
∴;
故选:D.
根据正六边形得到,然后利用三角形内角和求出的度数,最后根据平行线的性质得出.
6.C
7.D
8.D
9.C
设这个多边形的边数为n,由多边形的内角和是720°,根据多边形的内角和定理得(n-2)180°=720°.解得n=6.故答案为:C.
设这个多边形的边数为n,根据多边形的内角和定理得到(n﹣2)×180°=720°,然后解方程即可.
10.A
解:A:平行四边形面积为:
,则CD边上的高为
B:平行四边形面积为:
,则CD边上的高为
C:该平行四边形为正方形
,则CD边上的高为
D:平行四边形面积为:
,则CD边上的高为
故答案为:A
先求出平行四边形面积,再根据勾股定理求出CD长,再根据面积求出CD边上的高,比较大小即可求出答案.
11.C
解:∵四边形ABCD是平行四边形,AD=8
∴AD∥BC,AD=BC=9
∴△AGE∽△CGB
∴
∵
∴
∵CB=9
∴AE=3
∴DE=AD-AE=6
故答案为:C
根据平行四边形性质可得AD∥BC,AD=BC=9,再根据相似三角形判定定理可得△AGE∽△CGB,则,根据题意可得AE=3,再根据边之间的关系即可求出答案.
12.A
13.B
14.B
15.B
16.C
17.C
解:A、一组对边平行,另一组对边相等的四边形可能是平行四边形也可能是等腰梯形,故原命题错误,不符合题意;
B、有一个角是直角且对角线互相平分的四边形是矩形,故原命题错误,不符合题意;
C、顺次连接矩形各边中点得到的四边形是菱形,正确,符合题意;
D、对角线互相垂直且相等的平行四边形是正方形,故原命题错误,不符合题意.
故答案为:C.
利用平行四边形、矩形、菱形及正方形的判定方法分别判断后即可确定正确的选项.
18.D
19.D
解:∵菱形中,,垂足为,
∴,,
∴,,
∵点在线段上,过点作,
∴,四边形是平行四边形,
∴,,
∴,
∵,
∴,
∴,整理得:,
解得:或(不合题意舍弃).
故选:D.
根据菱形性质可得,,再根据等腰直角三角形的性质以及勾股定理可得、,过点作,根据平行四边形判定定理可得四边形是平行四边形,则,,再根据边之间的关系可得,,再根据三角形面积化简即可求出答案.
20.A
21.A
解:∵四边形ABCD是平行四边形,
∴OA=OC,及O为AC的中点,
∵ E是AB的中点,
∴OE是△ABC的中位线,
∴OE∥BC,
∴∠AOE=∠ACB=88°;
故答案为:A.
根据平行四边形的性质及中点的定义判定OE为三角形中位线,根据中位线定理即可得解.
22.B
23.A
24.B
25.C
26.B
27.B
28.B
29.C
解:
如图,五个全等的等腰三角形拼成内外两个正五边形,
∴∠ABD==108°,∠DBC=∠BAC,
∵∠α+∠ACB+∠BAC=180°,
∴∠ACB=∠BAC=180°-108°=72°,
∴∠α=180°-∠ACB-∠BAC=180°-72°-72°=36°,
故答案为:C.
根据题目描述,五个完全相同的等腰三角形组合构成了内外两个正五边形,通过计算正五边形的内角可知∠ABD为108度,运用三角形内角和为180度的性质,可以推导出∠ACB和∠BAC均为72度(180°-108°),最终即可求得∠α的具体数.
30.C
解:连接OE,如图所示:
由条件可知AB=CD=5,,AO=CO,AD=BC=y,AD//BC,,
∵E为BC的中点,O为BD的中点,
∴OE//CD,,
∴△OPE∽△CPD,
∴
∴,,
∵DE⊥AC,
∴∠OPE=∠EPC=∠CPD=∠OPD=90°,
根据勾股定理得:,
PC2+PD2=52,,
∴,PC2+PD2=25,,
∴,,
∴,
∴x2+y2=5PC2+5PD2=5×25=125,
∴x2+y2为定值.
故答案为:C.
连接OE,根据平行四边形的性质得出AB=CD=5,,AO=CO,AD=BC=y,AD//BC,根据中位线性质得出OE//CD,,证明△OPE∽△CPD,得出,根据勾股定理,即可得出答案.
31.A
32.C
33.C
34.C
35.A
36.D
37.D
38.B
39.D
解:当移动时间为8秒时,OE=8,BF=8
∵四边形OABC是矩形
∴OA=BC,OA∥BC,∠AOC=90°
∵点A的坐标为(18,0)
∴OA=18
∴BC=18
∴AE=10,CF=10
∴AE=CF
∵OA∥BC
∴四边形AECF是平行四边形
∵点C的坐标为(0,6)
∴OC=6
在Rt△COE中,由勾股定理可得
∴CE=AE
∴四边形AECF是菱形
连接AC,EF,则AC⊥EF
∴
∴=2×10×6=120
故答案为:D
当移动时间为8秒时,OE=8,BF=8,根据矩形性质可得OA=BC,OA∥BC,∠AOC=90°,根据点的坐标可得OA=18,再根据边之间的关系可得AE=CF,再根据平行四边形判定定理可得四边形AECF是平行四边形,根据勾股定理可得CE,再根据菱形判定定理可得四边形AECF是菱形,连接AC,EF,则AC⊥EF,再根据菱形面积即可求出答案.
40.
41.12
42.24
43.(1);
44.
45.
46.
47.
解:如图,连接AA',
∵四边形ABCD是平行四边形,
∴AD//BC
∵FG//AB,
∴四边形ABFG是平行四边形,
∴AB=GF,AG=BF,
由折叠可得:四边形A'GFB'是平行四边形,
∴A'B'=GF,A'B'//GF//AB,
∴AB=GF=A'B',
∵由对折可得:AB=A'B',FB=FB',AG=A'G,BE=B'E,
∴
∴HG=AG=A'G,
∴A'在以G为圆心,AH为直径的圆上,
∴∠AA'H=90°,
∵AD//BC,
∴△DGE∽△BFE,
∴,
∴,而AG+ DG= AD= 28,
∴AG=8,DG=20,
∴HG=AG=A'G=8,
∴AH=16,DH=12,
∵A'H = DH,
∴A'H=DH=12,
∴,
∴
∵AB//A'B',AB=A'B',
∴四边形ABB'A'为平行四边形,
∴AA'//DB',
∴△AA'H∽△DB'H,
∴
∴,
故答案为:.
如图,连接AA',由折叠可得:四边形A'GFB'是平行四边形,可得A'B'=GF,A'B'//GF//AB,AB=GF=A'B',,证明,HG=AG=A'G,可得A'在以G为圆心,AH为直径的圆上,∠AA'H=90°,证明出△DGE∽△BFE,可得AG=8,DG=20,,,再进一步利用相似三角形的性质,即可得出结论.
48.135
49.
50.
同课章节目录
