专题21 特殊的四边形(50 题)【最新中考模拟题】-2025学年中考数学满分冲刺(全国通用)(含答案+解析)
文档属性
| 名称 | 专题21 特殊的四边形(50 题)【最新中考模拟题】-2025学年中考数学满分冲刺(全国通用)(含答案+解析) |

|
|
| 格式 | docx | ||
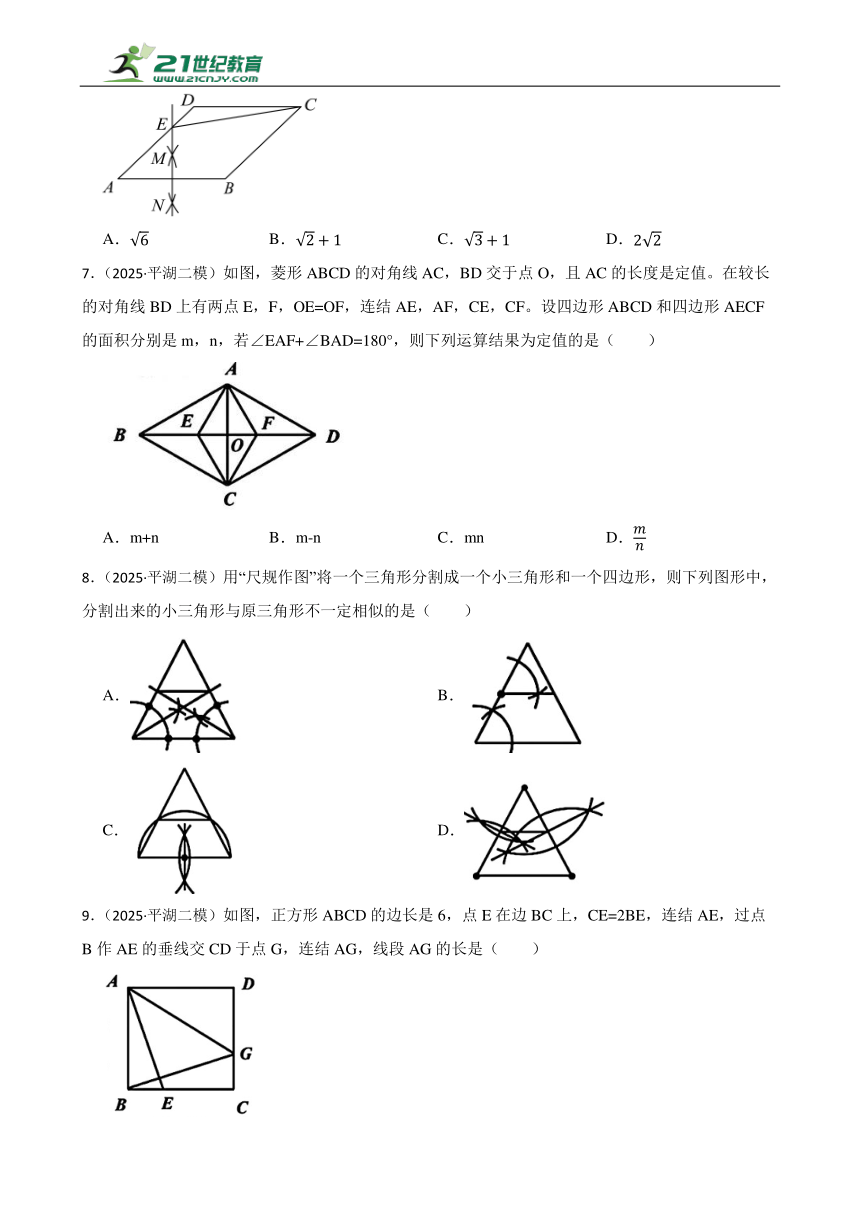
| 文件大小 | 947.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-06 22:23:01 | ||
图片预览

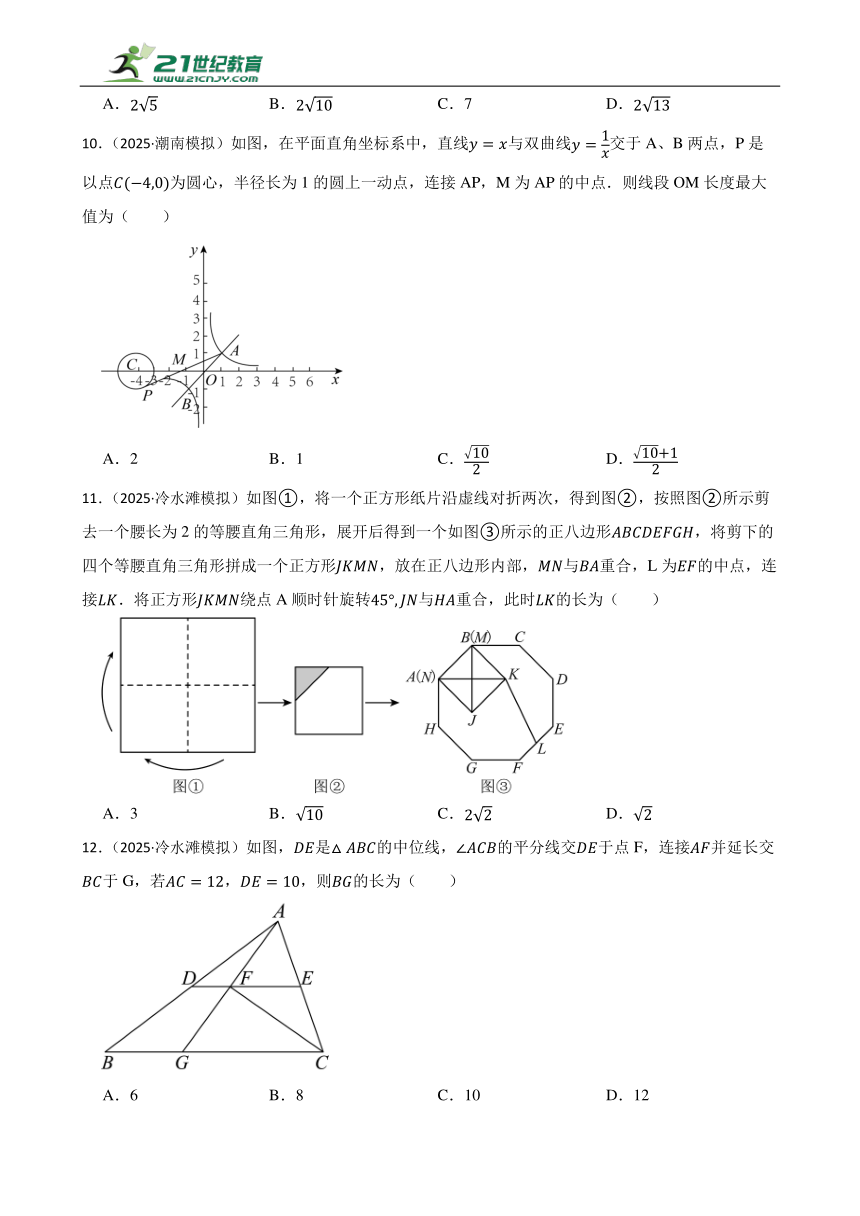


文档简介
2025学年中考数学满分冲刺(全国通用)【最新中考模拟题】
专题21 特殊的四边形(50 题)
一、选择题
1.(2025·从江模拟)在菱形中,两条对角线相交于点O,下列结论不一定成立的是( )
A. B. C. D.
2.(2025·合江模拟)已知菱形的边长为6,一个内角为60°,则菱形较长的对角线长是( )
A. B. C.3 D.6
3.(2025·织金模拟)如图,在平行四边形中,,E,F分别是的中点,连接,则( )
A.2 B.3 C.8 D.无法确定
4.(2025·路桥二模)如图,四边形ABCD是矩形,对角线AC,BD相交于点,若,则OB的长为( )
A.1 B.2 C.3 D.4
5.(2025·仁寿模拟)下列命题中,是假命题的是( )
A.圆周角等于圆心角的一半
B.任意多边形的外角和都是360°
C.对角线互相垂直的平行四边形是菱形
D.平移不改变图形的形状和大小
6.(2025·深圳三模)如图,在菱形中,,分别以点A和B为圆心,以大于的长为半径作弧,两弧相交于点M和N,作直线,交于点E,连接,若,则的长为( )
A. B. C. D.
7.(2025·平湖二模)如图,菱形ABCD的对角线AC,BD交于点O,且AC的长度是定值。在较长的对角线BD上有两点E,F,OE=OF,连结AE,AF,CE,CF。设四边形ABCD和四边形AECF的面积分别是m,n,若∠EAF+∠BAD=180°,则下列运算结果为定值的是( )
A.m+n B.m-n C.mn D.
8.(2025·平湖二模)用“尺规作图”将一个三角形分割成一个小三角形和一个四边形,则下列图形中,分割出来的小三角形与原三角形不一定相似的是( )
A. B.
C. D.
9.(2025·平湖二模)如图,正方形ABCD的边长是6,点E在边BC上,CE=2BE,连结AE,过点B作AE的垂线交CD于点G,连结AG,线段AG的长是( )
A. B. C.7 D.
10.(2025·潮南模拟)如图,在平面直角坐标系中,直线与双曲线交于A、B两点,P是以点为圆心,半径长为1的圆上一动点,连接AP,M为AP的中点.则线段OM长度最大值为( )
A.2 B.1 C. D.
11.(2025·冷水滩模拟)如图①,将一个正方形纸片沿虚线对折两次,得到图②,按照图②所示剪去一个腰长为2的等腰直角三角形,展开后得到一个如图③所示的正八边形,将剪下的四个等腰直角三角形拼成一个正方形,放在正八边形内部,与重合,L为的中点,连接.将正方形绕点A顺时针旋转与重合,此时的长为( )
A.3 B. C. D.
12.(2025·冷水滩模拟)如图,是的中位线,的平分线交于点F,连接并延长交于G,若,,则的长为( )
A.6 B.8 C.10 D.12
13.(2025·浙江模拟) 如图,在菱形 ABCD 中,对角线 AC, BD 相交于点 O,E 是线段 BO 上的一点,连结 AE,。若 ,AC 的长为 ,则 AB 的长为( )
A. B. C. D.
14.(2025·浙江二模)如图,矩形ABCD,点在边AD上,连结BE,CE.若,则CE的长为( )
A. B. C. D.
15.(2025·普陀二模)如图,在矩形ABCD中,E、F分别为CD、AB上的点,且ED=2BF,连结 CF、EF、DF,其中∠CFE=∠CDF,CF=2,则 DF=( )
A. B.3 C. D.
16.(2025·钱塘二模)下列命题正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.有一个角是直角且对角线相等的四边形是矩形
C.顺次连结矩形各边中点得到的四边形是菱形
D.对角线互相垂直且相等的四边形是正方形
17.(2025·诸暨二模) 已知反比例函数 ),第一象限有一点P,过P向坐标轴作垂线,分别交x轴,y轴于A,B点,分别交反比例函数于C,D点,若,,则( )
A.2 B.3 C.4 D.5
18.(2025·诸暨二模) 如图,在正方形 ABCD 中,点 P 是 AB 上一动点(不与 A, B 重合),对角线 AC, BD 相交于点 O,过点 P 分别作 AC, BD 的垂线,分别交 AC, BD 于点 E 与点 F,交 AD, BC 于点 G 与点 H,若正方形的边长是 2,则四边形 OEPF 的周长是( )
A.2 B. C.4 D.
19.(2025·深圳模拟)如图,菱形中,,垂足为,点在线段上,过点作,,则的值为( )
A. B. C.1 D.
20.(2025·黄岩二模)如图,已知的半径长是2,BA,BC分别切于点A,C,连结BO并延长交于点,连结AD,CD.若四边形ABCD是菱形,则BD的长是( )
A.5 B. C.6 D.
21.(2025·椒江二模)菱形ABCD与3个全等的正六边形按如图放置,若正六边形的边长为a,则菱形ABCD的边长为( )
A.2a B.2a C.3a D.4a
22.(2025·玉环二模)如图,在矩形ABCD中,BC>AB,先以点A为圆心,AB长为半径画弧交边AD于点E;再以点D为圆心,DE长为半径画弧交边DC于点F;最后以点C为圆心,CF长为半径画弧交边BC于点G.求BG的长,只需要知道( )
A.线段AB的长 B.线段AD的长 C.线段DE的长 D.线段CF的长
23.(2025·温岭二模)如图,大正方形ABCD由四个全等的直角三角形和中间一个小正方形EFGH组成,,较短直角边与较长直角边和为5,则正方形ABCD的面积为( )
A.5 B. C.10 D.13
24.(2025·福田模拟)如图,在矩形中,边绕点B顺时针旋转到的位置,点A的对应点E落在边的中点,若,则点A旋转到点E的路径长为( )
A. B. C. D.
25.(2025·广汉模拟)某乡镇的4个村庄A、B、C、D恰好位于正方形的4个顶点上,为了解决农民出行难问题,镇政府决定修建连接各村庄的道路系统,使得每两个村庄都有直达的公路,设计人员给出了如下四个设计方案(实线表示连接的道路)
在上述四个方案中最短的道路系统是方案( )
A.一 B.二 C.三 D.四
26.(2025·旌阳模拟)如图,将矩形沿翻折,使点B落在上的点F处,射线与矩形的外角的平分线相交于点,若,,则线段的长为( )
A. B. C. D.
27.(2025·顺庆模拟)如图,是等边的外接圆,,分别为,的中点,延长交于点,若的半径,则的长度为( )
A. B. C. D.
28.(2025·高坪模拟)如图,在正方形中,对角线,相交于点,点在边上,且,连接交于点,过点作,连接并延长,交于点,过点作分别交,于点、,交的延长线于点,现给出下列结论:①;②;③;④.其中正确的结论个数为( )
A.1 B.2 C.3 D.4
29.(2025·乐清二模)如图,在矩形ABCD中,是BC上一点,交AD于点,交对角线AC于点,连接BG,DG,DE.若求阴影部分的面积,则只需要知道( )
A.的面积 B.的面积
C.四边形ABEF的面积 D.四边形CDFE的面积
30.(2025·仁寿模拟)如图,在正方形纸片中,是边的中点,将正方形纸片沿折叠,点落在点处,延长交于点,连接并延长交于点.给出以下结论:
①为等腰三角形;②四边形AECF是平行四边形
③;④.其中正确的结论是( )
A.①② B.①②④ C.②③④ D.①②③
二、填空题
31.(2025·花垣模拟)如图,已知中,,,,M为边上的一个动点,,,则的最小值为 .
32.(2025·金华模拟)如图,四边形中,,,连接,点分别是的中点,则 .
33.(2025·深圳模拟)如图,在平面直角坐标系中,正方形的对角线在x轴的正半轴上,顶点A在反比例函数的图象上,若正方形的周长为,则k的值为 .
34.(2025·冷水滩模拟)如图,矩形的顶点A,C分别在y轴、x轴的正半轴上,且,反比例函数的图象经过点D及矩形的对称中心M,连接.若的面积为3,则k的值为 .
35.(2025·宁海模拟)如图,在矩形中,O为坐标原点,点B在x轴负半轴上,点C在y轴正半轴上,双曲线分别交AC,AB于点D,E,AD=3CD,以ED为边向下方作 DEFG,使 DEFG与矩形面积相等,连结OF,OG,则 ,的面积是 .
36.(2025·宁海模拟)如图,D,E分别是△ABC边AB,AC的中点,点F是AE的中点,连结DE,BF交于点G,
若EG=5,则DG= .
37.(2025·武冈模拟)已知抛物线与x轴交于A,B两点,对称轴与抛物线交于点C,与x轴交于点D,的半径为1,G为上一动点,P为的中点,则的最大值为 .
38.(2025·玉环二模)如图,在中,平分,点是BC的中点,连接DE,则DE的长为 .
39.(2025·金东二模) 将一个矩形按如图所示方式分割成三个相似的直角三角形,按面积从大到小的顺序分别记为,,。将、叠合,得到图1,阴影部分的三角形面积记为;将、叠合,得到图2,阴影部分的四边形面积记为。若,则该矩形的长和宽之比为 。
40.(2025·凉州模拟)如图,矩形中,,将矩形绕着点顺时针旋转得矩形,恰好落在对角线上,连接,如果与边相交,且,那么的长是 .
41.(2025·祁阳模拟)如图,平行四边形中,点是对角线的中点,点在边上,连接,取的中点,连接并延长交于点.若,,则线段的长是 .
42.(2025·文成二模)如图,在中,分别是AB,AC边上的中点,于点,过点作交BC于点,连结GF,则GF的长为 .
43.(2025·路桥二模)如图,D,E分别是的边AB,AC的中点,将线段DE沿AC方向平移得到线段FC,若,则AC的长是 cm.
44.(2025·合江模拟)如图,是等边三角形的边上的动点,连接,将绕点逆时针旋转,得到,连接,,若,则的最小值为 .
45.(2025·平湖二模)如图,点,均在反比例函数的图象上。连结AO,BO并延长,分别与反比例函数的图象交于点,,连结AB,,,。若,,则的值为 .
46.(2025·黄埔模拟)如图,在正方形纸片中,是边的中点,将正方形纸片沿折叠,点落在点处,延长交于点,连结并延长交于点.给出以下结论:①为等腰三角形;②为的中点;③;④.其中正确结论是 .(填序号)
47.(2024·随县模拟)如图.在△ABC中,∠ACB=60°,AC=1,D是边AB的中点,E是边BC上一点.若DE平分△ABC的周长,则DE的长是 .
48.(2025·凉州模拟)如图,点为正方形的边上两个动点,且,,连接,过点作,垂足为,连接,则面积的最大值为 .
49.(2025·邛崃模拟)如图,在矩形中,点为矩形对角线的中点,点为上一点,点为射线上一点,若,,则的最小值为 .
50.(2025·路桥二模)如图,把正方形ABCD的边DA绕点逆时针旋转,得到线段DF,连接BF并延长交DA于点,连接CE,若,则的值是 。
答案解析部分
1.D
2.B
3.B
4.B
5.A
6.A
7.C
8.A
9.D
10.D
11.B
12.B
13.A
14.A
解:在矩形ABCD中,AB=3,BC=BE=5,
∴AD=BC=5,AB=DC=3,∠A=∠D=90°,
在直角三角形ABE中,由勾股定理得:
,
∴DE=5-4=1,
在直角三角形CDE中,由勾股定理得:
,
故答案为:A.
先求出AD=BC=5,AB=DC=3,再根据勾股定理求出DB,进而求出结论.
15.A
解:在矩形ABCD中,AB=CD,AD=BC,
∠A=∠B=90°,
∵∠CFE=∠CDF,∠FCE=∠DCF,
∴△CFE~△CDF,
∴,
由ED=2BF,CF=2
设CD=AB=m,BF=x,ED=2x,
AF=m-x,AD=BC=y,
∴,
∴m2-2mx =4,
在Rt△BCF中,BC2+BF2=FC2,即
y2+x2= 22= 4,
在Rt△ADF中
DF2=AF2+AD2=y(m-x) 2+y2=m2-2mx+x2+y2=4+4=8,
∴DF =,
故答案为:A.
根据矩形的性质,设CD=AB=m,BF=x,ED=2x,AF=m-x,AD=BC=y,先证明△CFE~△CDF,得出关于m,x的方程,在Rt△BCF中,根据勾股定理得出关于x,y的方程,最后在Rt△ADF中,利用勾股定理即可求得DF.
16.C
解:A、一组对边平行,另一组对边相等的四边形可能是平行四边形也可能是等腰梯形,故原命题错误,不符合题意;
B、有一个角是直角且对角线互相平分的四边形是矩形,故原命题错误,不符合题意;
C、顺次连接矩形各边中点得到的四边形是菱形,正确,符合题意;
D、对角线互相垂直且相等的平行四边形是正方形,故原命题错误,不符合题意.
故答案为:C.
利用平行四边形、矩形、菱形及正方形的判定方法分别判断后即可确定正确的选项.
17.B
18.B
19.D
解:∵菱形中,,垂足为,
∴,,
∴,,
∵点在线段上,过点作,
∴,四边形是平行四边形,
∴,,
∴,
∵,
∴,
∴,整理得:,
解得:或(不合题意舍弃).
故选:D.
根据菱形性质可得,,再根据等腰直角三角形的性质以及勾股定理可得、,过点作,根据平行四边形判定定理可得四边形是平行四边形,则,,再根据边之间的关系可得,,再根据三角形面积化简即可求出答案.
20.C
解:连接AO,CO,
∵四边形ABCD是菱形,
∴AB=AD,
∴∠ABD=∠ADB,
由圆周角定理得:∠AOB=2∠ADB,
∴∠AOB=2∠ABD,
∵BA切⊙O于点A,
∴OA⊥AB,
∴∠BAO=90°,
∴∠AOB+∠ABD=90°,
∴∠ABO=30°,
∵AO=2,
∴OB=2OA=4,
∴BD=OB+OD=6,
故答案为:C.
连接AO,CO,根据萎形的性质得到AB=AD,求得∠ABD=∠ADB,根据圆周角定理即可得到∠AOB=2∠ABD,根据切线的性质得到∠BAO=90°,即可得到∠ABO的度数,根据含30°角直角三角形的性质可得OB的长度,进而可得BD的长度.
21.D
解:如图,由正六边形的性质以及菱形的性质可知,
AE=AE=EF=EG=CH=HD
∴当正六边形的边长为a,则菱形ABCD的边长为4a,
故答案为:D.
根据正六边形的性质以及菱形的性质进行计算即可.
22.C
解:∵四边形ABCD是矩形,
∴AB=CD,AD=BC,
∵AB=AE,DE=DF,CF=CG,
∴设AB=AE=CD=x,CF=CG=y,
∴DE=DF=x-y,
∴AD=BC=x+x-y,
∴BG=BC-CG=2x-y-y=2(x-y)=2DE,
∴求BG的长,只需要知道线段DE的长即可;
故答案为:C.
根据矩形的对边相等可得AB=CD,AD=BC,结合图可设AB=AE=CD=x,CF=CG=y,求得BG=BC-CG=2x-y-y=2(x-y)=2DE,即可得出结论.
23.D
解:设直角三角形较短直角边为a,较长直角边为b,
由题意得a+b=5,即a2+b2+2ab=25①,EH=EF=b-a,
∵,
∴(b-a)2+(b-a)2=FH2=2,
∴(b-a)2=1,
∴a2-2ab+b2=1②,
①+②得2(a2+b2)=26,
∴a2+b2=13,
∴正方形ABCD的面积为a2+b2=13,
故答案为:D.
设直角三角形较短直角边为a,较长直角边为b,由题意得a+b=5,求得a2+b2+2ab=25①,由,求得a2-2ab+b2=1②,据此求解即可.
24.B
解:在矩形中,,
∵边绕点B顺时针旋转到的位置,点A的对应点E落在边的中点,,
∴,
∴,
∴,
∴,
∴点A旋转到点E的路径长为,
故选:B
根据旋转性质可得,根据正弦定义及特殊角的三角函数值可得,根据余角可得,再根据弧长公式即可求出答案.
25.D
26.D
27.D
28.D
29.D
解:设AB=BE=x,EC=y,
由FE∥CD得,,
∴,
由GE∥AB得,△GEC∽△ABC,
∴,
即,
∴GE=
则===xy,
又∵SCDFE=EC·DC=xy=,
故答案为:D.
根据平行线间的距离相等,得到阴影部分面积为△GBC面积,设B=BE=x,EC=y,通过相似将GE用x,y的代数式表示,进而可表示△GBC的面积为xy,即为四边形CDFE的一半.
30.B
31.
32.3
33.4
34.4
35.3;
36.2.5
37.3
38.3
39.
解:由题意可得如图,
∵四边形C1B2B3A1是矩形,
∴C1B2=A1B3,
设A2B2=B3C3=a,B2C2=b,
∵△A1B1C1∽△A2B2C2∽△A3B3C3,
∴∠B1A1C1=∠B2A2C2,,
∴,
设图1中A1C1与A2C2交于一点E,过点E作EF⊥A1B1,垂足为F,如图所示,
∵∠B1A1C1=∠B2A2C2,
∴,
∵∠A2FE=∠A2B2C2=90°,∠FA2E=∠B2A2C2,
∴△A2FE∽△A2B2C2,
∴,
∴,
∴,
,
∵,
∴,
解得:(负根舍去),
∴,
∴该矩形的长和宽之比为.
故答案为:.
设,,由题意易得∠B1A1C1=∠B2A2C2,,则有,设图1中A1C1与A2C2交于一点E,过点E作EF⊥A1B1,垂足为F,然后可得,则有,进而问题可求解.
40.
41.
42.4
解:如图,连接ED交GF于点O,
∵AD⊥BC,
∴∠ADC=∠ADB=90°,
又∵点E、F分别是AB、AC的中点,
∴DF=AC=2.5,DE=AB=3,EF=BC=2.5,EF∥GD,
又∵EG∥DF,
∴四边形DFEG是平行四边形,
又∵DF=EF=2.5,
∴平行四边形DFEG是菱形,
∴ED⊥DF,GF=2OF,EO=ED=1.5,
∴OF=,
∴GF=2OF=4.
故答案为:4.
连接ED交GF于点O,由直角三角形斜边中线等于斜边的一半得DF=AC=2.5,DE=AB=3,由三角形的中位线平行于第三边且等于第三边的一半得EF=BC=2.5,EF∥GD,由“两组对边分别平行得四边形是平行四边形”得四边形DFEG是平行四边形,由“一组邻边相等的平行四边形是菱形”得平行四边形DFEG是菱形,由菱形对角线互相垂直平分得ED⊥DF,EO=ED=1.5,GF=2OF,进而利用勾股定理算出OF即可得出答案.
43.12
44.
45.6
46.①②③
47.
48.
49.
50.
专题21 特殊的四边形(50 题)
一、选择题
1.(2025·从江模拟)在菱形中,两条对角线相交于点O,下列结论不一定成立的是( )
A. B. C. D.
2.(2025·合江模拟)已知菱形的边长为6,一个内角为60°,则菱形较长的对角线长是( )
A. B. C.3 D.6
3.(2025·织金模拟)如图,在平行四边形中,,E,F分别是的中点,连接,则( )
A.2 B.3 C.8 D.无法确定
4.(2025·路桥二模)如图,四边形ABCD是矩形,对角线AC,BD相交于点,若,则OB的长为( )
A.1 B.2 C.3 D.4
5.(2025·仁寿模拟)下列命题中,是假命题的是( )
A.圆周角等于圆心角的一半
B.任意多边形的外角和都是360°
C.对角线互相垂直的平行四边形是菱形
D.平移不改变图形的形状和大小
6.(2025·深圳三模)如图,在菱形中,,分别以点A和B为圆心,以大于的长为半径作弧,两弧相交于点M和N,作直线,交于点E,连接,若,则的长为( )
A. B. C. D.
7.(2025·平湖二模)如图,菱形ABCD的对角线AC,BD交于点O,且AC的长度是定值。在较长的对角线BD上有两点E,F,OE=OF,连结AE,AF,CE,CF。设四边形ABCD和四边形AECF的面积分别是m,n,若∠EAF+∠BAD=180°,则下列运算结果为定值的是( )
A.m+n B.m-n C.mn D.
8.(2025·平湖二模)用“尺规作图”将一个三角形分割成一个小三角形和一个四边形,则下列图形中,分割出来的小三角形与原三角形不一定相似的是( )
A. B.
C. D.
9.(2025·平湖二模)如图,正方形ABCD的边长是6,点E在边BC上,CE=2BE,连结AE,过点B作AE的垂线交CD于点G,连结AG,线段AG的长是( )
A. B. C.7 D.
10.(2025·潮南模拟)如图,在平面直角坐标系中,直线与双曲线交于A、B两点,P是以点为圆心,半径长为1的圆上一动点,连接AP,M为AP的中点.则线段OM长度最大值为( )
A.2 B.1 C. D.
11.(2025·冷水滩模拟)如图①,将一个正方形纸片沿虚线对折两次,得到图②,按照图②所示剪去一个腰长为2的等腰直角三角形,展开后得到一个如图③所示的正八边形,将剪下的四个等腰直角三角形拼成一个正方形,放在正八边形内部,与重合,L为的中点,连接.将正方形绕点A顺时针旋转与重合,此时的长为( )
A.3 B. C. D.
12.(2025·冷水滩模拟)如图,是的中位线,的平分线交于点F,连接并延长交于G,若,,则的长为( )
A.6 B.8 C.10 D.12
13.(2025·浙江模拟) 如图,在菱形 ABCD 中,对角线 AC, BD 相交于点 O,E 是线段 BO 上的一点,连结 AE,。若 ,AC 的长为 ,则 AB 的长为( )
A. B. C. D.
14.(2025·浙江二模)如图,矩形ABCD,点在边AD上,连结BE,CE.若,则CE的长为( )
A. B. C. D.
15.(2025·普陀二模)如图,在矩形ABCD中,E、F分别为CD、AB上的点,且ED=2BF,连结 CF、EF、DF,其中∠CFE=∠CDF,CF=2,则 DF=( )
A. B.3 C. D.
16.(2025·钱塘二模)下列命题正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.有一个角是直角且对角线相等的四边形是矩形
C.顺次连结矩形各边中点得到的四边形是菱形
D.对角线互相垂直且相等的四边形是正方形
17.(2025·诸暨二模) 已知反比例函数 ),第一象限有一点P,过P向坐标轴作垂线,分别交x轴,y轴于A,B点,分别交反比例函数于C,D点,若,,则( )
A.2 B.3 C.4 D.5
18.(2025·诸暨二模) 如图,在正方形 ABCD 中,点 P 是 AB 上一动点(不与 A, B 重合),对角线 AC, BD 相交于点 O,过点 P 分别作 AC, BD 的垂线,分别交 AC, BD 于点 E 与点 F,交 AD, BC 于点 G 与点 H,若正方形的边长是 2,则四边形 OEPF 的周长是( )
A.2 B. C.4 D.
19.(2025·深圳模拟)如图,菱形中,,垂足为,点在线段上,过点作,,则的值为( )
A. B. C.1 D.
20.(2025·黄岩二模)如图,已知的半径长是2,BA,BC分别切于点A,C,连结BO并延长交于点,连结AD,CD.若四边形ABCD是菱形,则BD的长是( )
A.5 B. C.6 D.
21.(2025·椒江二模)菱形ABCD与3个全等的正六边形按如图放置,若正六边形的边长为a,则菱形ABCD的边长为( )
A.2a B.2a C.3a D.4a
22.(2025·玉环二模)如图,在矩形ABCD中,BC>AB,先以点A为圆心,AB长为半径画弧交边AD于点E;再以点D为圆心,DE长为半径画弧交边DC于点F;最后以点C为圆心,CF长为半径画弧交边BC于点G.求BG的长,只需要知道( )
A.线段AB的长 B.线段AD的长 C.线段DE的长 D.线段CF的长
23.(2025·温岭二模)如图,大正方形ABCD由四个全等的直角三角形和中间一个小正方形EFGH组成,,较短直角边与较长直角边和为5,则正方形ABCD的面积为( )
A.5 B. C.10 D.13
24.(2025·福田模拟)如图,在矩形中,边绕点B顺时针旋转到的位置,点A的对应点E落在边的中点,若,则点A旋转到点E的路径长为( )
A. B. C. D.
25.(2025·广汉模拟)某乡镇的4个村庄A、B、C、D恰好位于正方形的4个顶点上,为了解决农民出行难问题,镇政府决定修建连接各村庄的道路系统,使得每两个村庄都有直达的公路,设计人员给出了如下四个设计方案(实线表示连接的道路)
在上述四个方案中最短的道路系统是方案( )
A.一 B.二 C.三 D.四
26.(2025·旌阳模拟)如图,将矩形沿翻折,使点B落在上的点F处,射线与矩形的外角的平分线相交于点,若,,则线段的长为( )
A. B. C. D.
27.(2025·顺庆模拟)如图,是等边的外接圆,,分别为,的中点,延长交于点,若的半径,则的长度为( )
A. B. C. D.
28.(2025·高坪模拟)如图,在正方形中,对角线,相交于点,点在边上,且,连接交于点,过点作,连接并延长,交于点,过点作分别交,于点、,交的延长线于点,现给出下列结论:①;②;③;④.其中正确的结论个数为( )
A.1 B.2 C.3 D.4
29.(2025·乐清二模)如图,在矩形ABCD中,是BC上一点,交AD于点,交对角线AC于点,连接BG,DG,DE.若求阴影部分的面积,则只需要知道( )
A.的面积 B.的面积
C.四边形ABEF的面积 D.四边形CDFE的面积
30.(2025·仁寿模拟)如图,在正方形纸片中,是边的中点,将正方形纸片沿折叠,点落在点处,延长交于点,连接并延长交于点.给出以下结论:
①为等腰三角形;②四边形AECF是平行四边形
③;④.其中正确的结论是( )
A.①② B.①②④ C.②③④ D.①②③
二、填空题
31.(2025·花垣模拟)如图,已知中,,,,M为边上的一个动点,,,则的最小值为 .
32.(2025·金华模拟)如图,四边形中,,,连接,点分别是的中点,则 .
33.(2025·深圳模拟)如图,在平面直角坐标系中,正方形的对角线在x轴的正半轴上,顶点A在反比例函数的图象上,若正方形的周长为,则k的值为 .
34.(2025·冷水滩模拟)如图,矩形的顶点A,C分别在y轴、x轴的正半轴上,且,反比例函数的图象经过点D及矩形的对称中心M,连接.若的面积为3,则k的值为 .
35.(2025·宁海模拟)如图,在矩形中,O为坐标原点,点B在x轴负半轴上,点C在y轴正半轴上,双曲线分别交AC,AB于点D,E,AD=3CD,以ED为边向下方作 DEFG,使 DEFG与矩形面积相等,连结OF,OG,则 ,的面积是 .
36.(2025·宁海模拟)如图,D,E分别是△ABC边AB,AC的中点,点F是AE的中点,连结DE,BF交于点G,
若EG=5,则DG= .
37.(2025·武冈模拟)已知抛物线与x轴交于A,B两点,对称轴与抛物线交于点C,与x轴交于点D,的半径为1,G为上一动点,P为的中点,则的最大值为 .
38.(2025·玉环二模)如图,在中,平分,点是BC的中点,连接DE,则DE的长为 .
39.(2025·金东二模) 将一个矩形按如图所示方式分割成三个相似的直角三角形,按面积从大到小的顺序分别记为,,。将、叠合,得到图1,阴影部分的三角形面积记为;将、叠合,得到图2,阴影部分的四边形面积记为。若,则该矩形的长和宽之比为 。
40.(2025·凉州模拟)如图,矩形中,,将矩形绕着点顺时针旋转得矩形,恰好落在对角线上,连接,如果与边相交,且,那么的长是 .
41.(2025·祁阳模拟)如图,平行四边形中,点是对角线的中点,点在边上,连接,取的中点,连接并延长交于点.若,,则线段的长是 .
42.(2025·文成二模)如图,在中,分别是AB,AC边上的中点,于点,过点作交BC于点,连结GF,则GF的长为 .
43.(2025·路桥二模)如图,D,E分别是的边AB,AC的中点,将线段DE沿AC方向平移得到线段FC,若,则AC的长是 cm.
44.(2025·合江模拟)如图,是等边三角形的边上的动点,连接,将绕点逆时针旋转,得到,连接,,若,则的最小值为 .
45.(2025·平湖二模)如图,点,均在反比例函数的图象上。连结AO,BO并延长,分别与反比例函数的图象交于点,,连结AB,,,。若,,则的值为 .
46.(2025·黄埔模拟)如图,在正方形纸片中,是边的中点,将正方形纸片沿折叠,点落在点处,延长交于点,连结并延长交于点.给出以下结论:①为等腰三角形;②为的中点;③;④.其中正确结论是 .(填序号)
47.(2024·随县模拟)如图.在△ABC中,∠ACB=60°,AC=1,D是边AB的中点,E是边BC上一点.若DE平分△ABC的周长,则DE的长是 .
48.(2025·凉州模拟)如图,点为正方形的边上两个动点,且,,连接,过点作,垂足为,连接,则面积的最大值为 .
49.(2025·邛崃模拟)如图,在矩形中,点为矩形对角线的中点,点为上一点,点为射线上一点,若,,则的最小值为 .
50.(2025·路桥二模)如图,把正方形ABCD的边DA绕点逆时针旋转,得到线段DF,连接BF并延长交DA于点,连接CE,若,则的值是 。
答案解析部分
1.D
2.B
3.B
4.B
5.A
6.A
7.C
8.A
9.D
10.D
11.B
12.B
13.A
14.A
解:在矩形ABCD中,AB=3,BC=BE=5,
∴AD=BC=5,AB=DC=3,∠A=∠D=90°,
在直角三角形ABE中,由勾股定理得:
,
∴DE=5-4=1,
在直角三角形CDE中,由勾股定理得:
,
故答案为:A.
先求出AD=BC=5,AB=DC=3,再根据勾股定理求出DB,进而求出结论.
15.A
解:在矩形ABCD中,AB=CD,AD=BC,
∠A=∠B=90°,
∵∠CFE=∠CDF,∠FCE=∠DCF,
∴△CFE~△CDF,
∴,
由ED=2BF,CF=2
设CD=AB=m,BF=x,ED=2x,
AF=m-x,AD=BC=y,
∴,
∴m2-2mx =4,
在Rt△BCF中,BC2+BF2=FC2,即
y2+x2= 22= 4,
在Rt△ADF中
DF2=AF2+AD2=y(m-x) 2+y2=m2-2mx+x2+y2=4+4=8,
∴DF =,
故答案为:A.
根据矩形的性质,设CD=AB=m,BF=x,ED=2x,AF=m-x,AD=BC=y,先证明△CFE~△CDF,得出关于m,x的方程,在Rt△BCF中,根据勾股定理得出关于x,y的方程,最后在Rt△ADF中,利用勾股定理即可求得DF.
16.C
解:A、一组对边平行,另一组对边相等的四边形可能是平行四边形也可能是等腰梯形,故原命题错误,不符合题意;
B、有一个角是直角且对角线互相平分的四边形是矩形,故原命题错误,不符合题意;
C、顺次连接矩形各边中点得到的四边形是菱形,正确,符合题意;
D、对角线互相垂直且相等的平行四边形是正方形,故原命题错误,不符合题意.
故答案为:C.
利用平行四边形、矩形、菱形及正方形的判定方法分别判断后即可确定正确的选项.
17.B
18.B
19.D
解:∵菱形中,,垂足为,
∴,,
∴,,
∵点在线段上,过点作,
∴,四边形是平行四边形,
∴,,
∴,
∵,
∴,
∴,整理得:,
解得:或(不合题意舍弃).
故选:D.
根据菱形性质可得,,再根据等腰直角三角形的性质以及勾股定理可得、,过点作,根据平行四边形判定定理可得四边形是平行四边形,则,,再根据边之间的关系可得,,再根据三角形面积化简即可求出答案.
20.C
解:连接AO,CO,
∵四边形ABCD是菱形,
∴AB=AD,
∴∠ABD=∠ADB,
由圆周角定理得:∠AOB=2∠ADB,
∴∠AOB=2∠ABD,
∵BA切⊙O于点A,
∴OA⊥AB,
∴∠BAO=90°,
∴∠AOB+∠ABD=90°,
∴∠ABO=30°,
∵AO=2,
∴OB=2OA=4,
∴BD=OB+OD=6,
故答案为:C.
连接AO,CO,根据萎形的性质得到AB=AD,求得∠ABD=∠ADB,根据圆周角定理即可得到∠AOB=2∠ABD,根据切线的性质得到∠BAO=90°,即可得到∠ABO的度数,根据含30°角直角三角形的性质可得OB的长度,进而可得BD的长度.
21.D
解:如图,由正六边形的性质以及菱形的性质可知,
AE=AE=EF=EG=CH=HD
∴当正六边形的边长为a,则菱形ABCD的边长为4a,
故答案为:D.
根据正六边形的性质以及菱形的性质进行计算即可.
22.C
解:∵四边形ABCD是矩形,
∴AB=CD,AD=BC,
∵AB=AE,DE=DF,CF=CG,
∴设AB=AE=CD=x,CF=CG=y,
∴DE=DF=x-y,
∴AD=BC=x+x-y,
∴BG=BC-CG=2x-y-y=2(x-y)=2DE,
∴求BG的长,只需要知道线段DE的长即可;
故答案为:C.
根据矩形的对边相等可得AB=CD,AD=BC,结合图可设AB=AE=CD=x,CF=CG=y,求得BG=BC-CG=2x-y-y=2(x-y)=2DE,即可得出结论.
23.D
解:设直角三角形较短直角边为a,较长直角边为b,
由题意得a+b=5,即a2+b2+2ab=25①,EH=EF=b-a,
∵,
∴(b-a)2+(b-a)2=FH2=2,
∴(b-a)2=1,
∴a2-2ab+b2=1②,
①+②得2(a2+b2)=26,
∴a2+b2=13,
∴正方形ABCD的面积为a2+b2=13,
故答案为:D.
设直角三角形较短直角边为a,较长直角边为b,由题意得a+b=5,求得a2+b2+2ab=25①,由,求得a2-2ab+b2=1②,据此求解即可.
24.B
解:在矩形中,,
∵边绕点B顺时针旋转到的位置,点A的对应点E落在边的中点,,
∴,
∴,
∴,
∴,
∴点A旋转到点E的路径长为,
故选:B
根据旋转性质可得,根据正弦定义及特殊角的三角函数值可得,根据余角可得,再根据弧长公式即可求出答案.
25.D
26.D
27.D
28.D
29.D
解:设AB=BE=x,EC=y,
由FE∥CD得,,
∴,
由GE∥AB得,△GEC∽△ABC,
∴,
即,
∴GE=
则===xy,
又∵SCDFE=EC·DC=xy=,
故答案为:D.
根据平行线间的距离相等,得到阴影部分面积为△GBC面积,设B=BE=x,EC=y,通过相似将GE用x,y的代数式表示,进而可表示△GBC的面积为xy,即为四边形CDFE的一半.
30.B
31.
32.3
33.4
34.4
35.3;
36.2.5
37.3
38.3
39.
解:由题意可得如图,
∵四边形C1B2B3A1是矩形,
∴C1B2=A1B3,
设A2B2=B3C3=a,B2C2=b,
∵△A1B1C1∽△A2B2C2∽△A3B3C3,
∴∠B1A1C1=∠B2A2C2,,
∴,
设图1中A1C1与A2C2交于一点E,过点E作EF⊥A1B1,垂足为F,如图所示,
∵∠B1A1C1=∠B2A2C2,
∴,
∵∠A2FE=∠A2B2C2=90°,∠FA2E=∠B2A2C2,
∴△A2FE∽△A2B2C2,
∴,
∴,
∴,
,
∵,
∴,
解得:(负根舍去),
∴,
∴该矩形的长和宽之比为.
故答案为:.
设,,由题意易得∠B1A1C1=∠B2A2C2,,则有,设图1中A1C1与A2C2交于一点E,过点E作EF⊥A1B1,垂足为F,然后可得,则有,进而问题可求解.
40.
41.
42.4
解:如图,连接ED交GF于点O,
∵AD⊥BC,
∴∠ADC=∠ADB=90°,
又∵点E、F分别是AB、AC的中点,
∴DF=AC=2.5,DE=AB=3,EF=BC=2.5,EF∥GD,
又∵EG∥DF,
∴四边形DFEG是平行四边形,
又∵DF=EF=2.5,
∴平行四边形DFEG是菱形,
∴ED⊥DF,GF=2OF,EO=ED=1.5,
∴OF=,
∴GF=2OF=4.
故答案为:4.
连接ED交GF于点O,由直角三角形斜边中线等于斜边的一半得DF=AC=2.5,DE=AB=3,由三角形的中位线平行于第三边且等于第三边的一半得EF=BC=2.5,EF∥GD,由“两组对边分别平行得四边形是平行四边形”得四边形DFEG是平行四边形,由“一组邻边相等的平行四边形是菱形”得平行四边形DFEG是菱形,由菱形对角线互相垂直平分得ED⊥DF,EO=ED=1.5,GF=2OF,进而利用勾股定理算出OF即可得出答案.
43.12
44.
45.6
46.①②③
47.
48.
49.
50.
同课章节目录
