第4章 几何图形初步 小结与复习课件(共26张PPT)
文档属性
| 名称 | 第4章 几何图形初步 小结与复习课件(共26张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 662.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-08 06:33:56 | ||
图片预览




文档简介
(共26张PPT)
小结与复习
第4章 几何图形初步
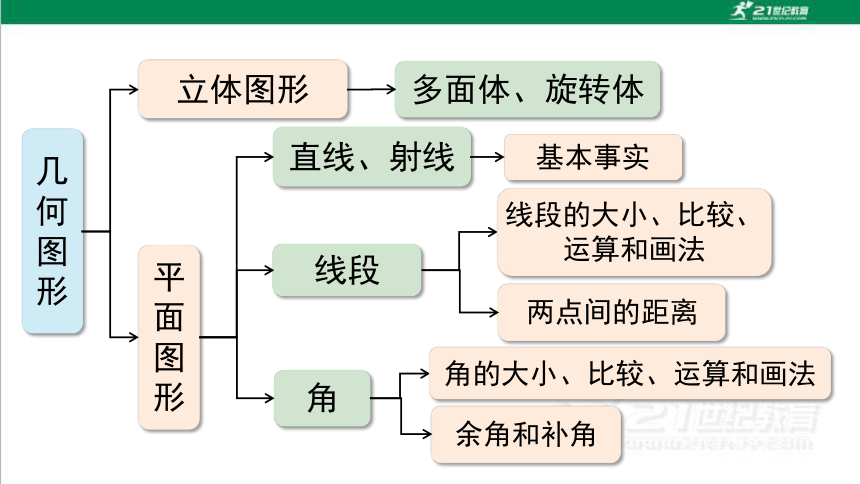
几何图形
立体图形
多面体、旋转体
两点间的距离
平面图形
线段的大小、比较、运算和画法
基本事实
直线、射线
线段
角
余角和补角
角的大小、比较、运算和画法
一、几何图形
1. 几何图形都是由点、线、面、体组成的.
2. 点、线、面、体之间的联系
(1) 体是由面围成,面与面相交成线,线与线相交成点;
(2) 点动成线、线动成面、面动成体.
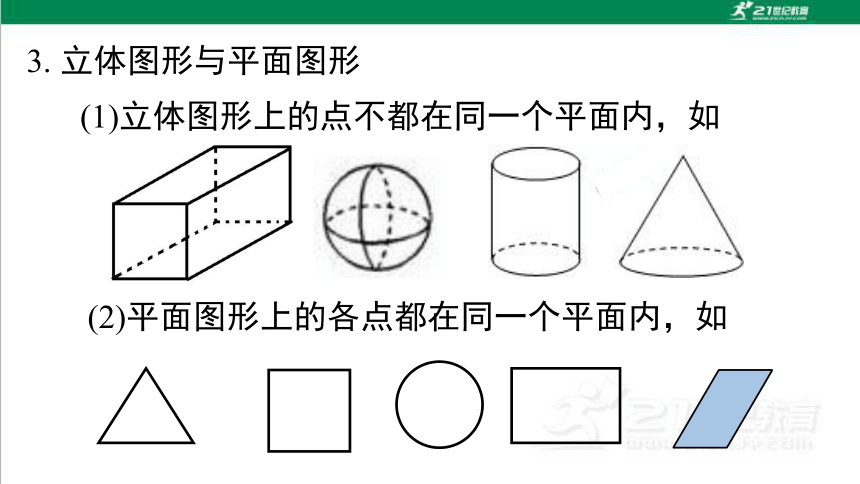
(2)平面图形上的各点都在同一个平面内,如
3. 立体图形与平面图形
(1)立体图形上的点不都在同一个平面内,如
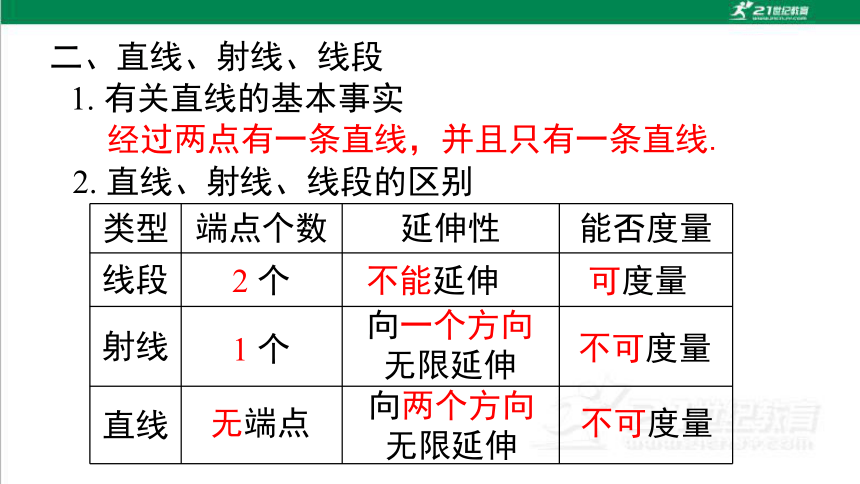
二、直线、射线、线段
1. 有关直线的基本事实
经过两点有一条直线,并且只有一条直线.
2. 直线、射线、线段的区别
类型 端点个数 延伸性 能否度量
线段
射线
直线
2 个
不能延伸
可度量
1 个
向一个方向
无限延伸
不可度量
无端点
向两个方向
无限延伸
不可度量
4. 有关线段的基本事实
两点之间线段最短
3. 线段的中点
应用格式:
A
C
B
因为 C 是线段 AB 的中点,
所以 AC = BC = AB,
AB = 2AC = 2BC.
5. 线段长短的比较方法
度量法或叠合法
三、角
1. 角的定义
(1) 从一个点出发的两条射线组成的图形,叫做角.
(2) 角也可以看做由一条射线绕着它的端点旋转所形成的图形.
2. 角的度量
度、分、秒的互化
1°=60′,1′=60″,
3. 角的大小的比较方法
度量法或叠合法
1″= ′,1′= °
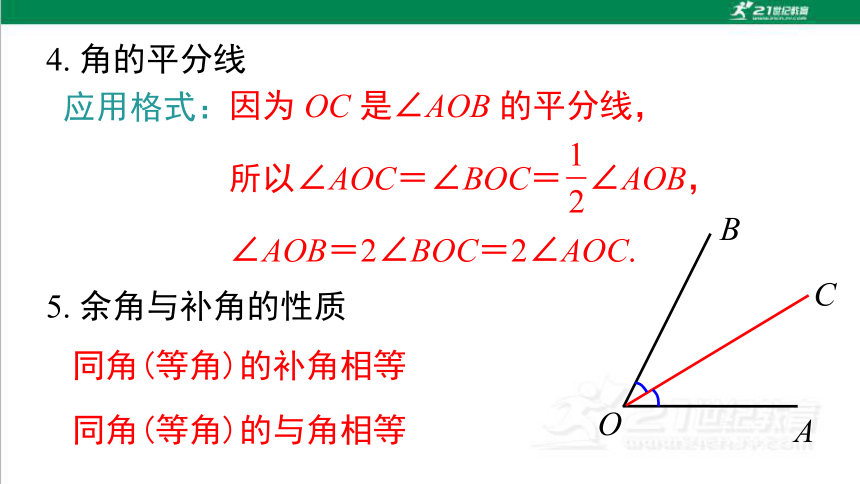
4. 角的平分线
O
B
A
C
应用格式:
5. 余角与补角的性质
同角(等角)的补角相等
同角(等角)的与角相等
因为 OC 是∠AOB 的平分线,
所以∠AOC=∠BOC= ∠AOB,
∠AOB=2∠BOC=2∠AOC.
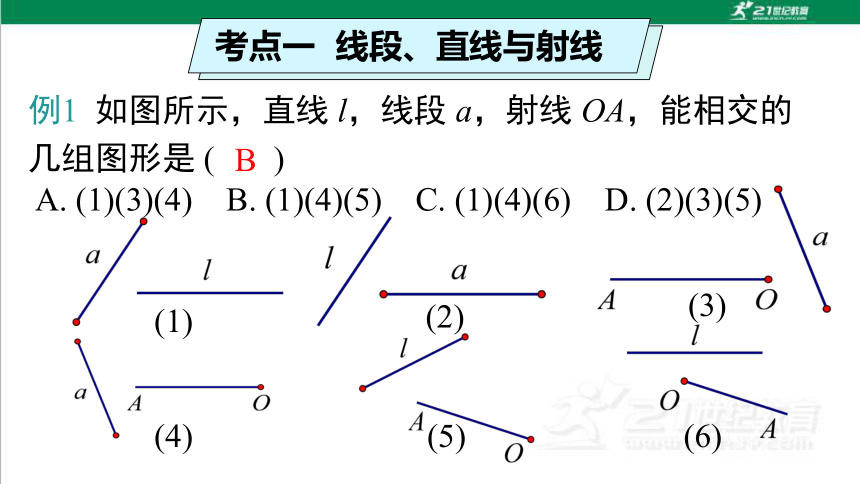
例1 如图所示,直线 l,线段 a,射线 OA,能相交的几组图形是 ( )
B
A. (1)(3)(4) B. (1)(4)(5) C. (1)(4)(6) D. (2)(3)(5)
(1)
(4) (5) (6)
(3)
(2)
考点一 线段、直线与射线
解析:此题相当于一条线段上有 3 个点,有多少种不同的票价即有多少条线段:4 + 3 + 2 + 1 = 10;有多少种车票是要考虑顺序的,则有 10×2 = 20.
1. 往返于甲、乙两地的火车中途要停靠三个站,则有______种不同的票价 (来回票价一样),需准备______种车票.
10
20
针对训练
例2 点 C 在线段 AB 所在的直线上,点 M,N 分别是 AC,BC 的中点.
(1) 如图,AC = 8 cm,CB = 6 cm,求线段 MN 的长;
A M C N B
所以 CM= AC=4 (cm),CN= BC=3 (cm).
解:因为点 M,N 分别是 AC,BC 的中点,
所以 MN=CM+CN=4+3=7 (cm).
考点二 线段长度的计算
(2) 若 C 为线段 AB 上任一点,满足 AC + CB = a cm,
其它条件不变,你能猜想 MN 的长度吗?并说明
理由;
A M C N B
理由:同(1)可得 CM = AC,CN = BC,
所以 MN = CM+CN = AC+ BC
= (AC+BC) = a (cm).
猜想:MN = a cm.
(3) 若C 在线段 AB的延长线上,且满足 AC-BC = b cm,
M,N 分别为 AC,BC 的中点,你能猜想 MN 的长
度吗?请画出图形,并说明理由.
A M B N C
MN = MC-NC = AC- BC
= (AC-BC) = b (cm).
猜想:MN = b cm.
理由:根据题意画出图形,由图可得
2. 已知:点 A,B,C 在一直线上,AB = 12 cm,BC =
4 cm. 点 M,N 分别是线段 AB,BC 的中点. 求线
段 MN 的长度.
A M C N B
图①
所以 BM = AB = ×12 = 6 (cm),
BN = BC = ×4 = 2 (cm).
解:如图①,当 C 在线段 AB 上时,
因为 M,N 分别是 AB,BC 的中点,
所以 MN = BM-BN = 6-2 = 4 (cm).
方法总结:无图条件下,注意多解情况要分类讨论,培养分类意识.
C
A
M
N
B
图②
所以 BM = AB = ×12 = 6 (cm),
BN = BC = ×4 = 2 (cm)
如图②,当 C 在线段 AB 外时,
因为 M,N 分别是 AB,BC 的中点,
所以 MN = BM + BN = 6 + 2 = 8 (cm).
考点三 角的度量及角度的计算
例3 45°52′48″=______°;
126.31°= ____°____′____″;
25°18′÷3=______;
126.31°=126°+0.31×60′=126°+18.6′
=126°18′+0.6×60″=126°18′36″.
解析:45°52′48″=45°+52′+(48÷60)′=45°+52.8′
=45°+(52.8÷60)°=45.88°.
25°18′÷3=8°+1°18′÷3=8°+78′÷3=8°26′.
45.88
126
18
36
8°26′
3. 若∠A=20°18′,∠B=20°15′30″,∠C=20.25°,则 ( )
A.∠A>∠B>∠C B.∠B>∠A>∠C
C.∠A>∠C>∠B D.∠C>∠A>∠B
A
4. 5 点整时,时钟上时针与分钟之间的夹角是 ( )
A. 210° B. 30° C. 150° D. 60°
C
针对训练
例4 如图,∠AOB 是直角,ON 是∠AOC 的平分线,OM 是∠BOC 的平分线.
(1) 当∠AOC = 50° 时,求∠MON 的大小;
O
B
M
A
N
C
提示:先求出∠BOC 的度数,再根据角平分线的定义求出∠COM,∠CON,然后根据∠MON =∠COM-∠CON
代入数据进行计算即可得解.
所以∠MON =∠COM-∠CON = 70°-25° = 45°.
解:因为∠AOB是直角,∠AOC = 50°, 所以∠BOC =∠AOB +∠AOC
= 90° + 50° = 140°.
因为 ON 是∠AOC 的平分线,
OM 是∠BOC 的平分线,
所以∠COM = ∠BOC = ×140° = 70°,
∠CON = ∠AOC = ×50° = 25°.
O
B
M
A
N
C
(2) 当∠AOC=α 时,∠MON 等于多少度?
O
B
M
A
N
C
所以∠MON =∠COM-∠CON = (90° + α)- α = 45°.
解:∠BOC =∠AOB +∠AOC = 90° + α.
因为 ON 是∠AOC 的平分线,
OM 是∠BOC 的平分线,
∠CON = ∠AOC = α.
所以∠COM = ∠BOC = (90° + α),
(3) 当锐角∠AOC 的大小发生改变时,∠MON 的大小
也会发生改变吗?为什么?
解:不会发生变化.
由 (2) 可知∠MON 的大小与∠AOC
无关,总是等于∠AOB 的一半.
O
B
M
A
N
C
5. 如图,长方形纸片 ABCD,点 E、F 分别在边 AB、CD 上,连接 EF.将∠BEF 对折,点 B 落在直线 EF 上的点 B' 处,得折痕 EM;将∠AEF 对折,点 A 落在直线 EF 上的点 A' 处,得折痕 EN,求∠NEM 的度数.
针对训练
解:由折纸过程可知, EM 平分∠BEB' ,EN 平分∠AEA'.
因为∠BEB'+∠AEA'=180°,
所以有∠NEM=∠NEA'+∠MEB'
所以有∠MEB'= ∠BEB',∠NEA'= ∠AEA'.
= (∠AEA'+∠BEB' ) =90°.
= ∠AEA'+ ∠BEB'
考点四 余角和补角
例5 已知∠α 和∠β 互为补角,并且∠β 的一半比∠α 小 30°,求∠α、∠β.
【解析】设∠α=x°,用 x 表示出∠β,列出方程即可.
解:设∠α=x°,则∠β=180°-x°.
根据题意 ∠β=2(∠α-30°),
即 180- x=2(x -30),
解得 x=80.
所以 ,∠α=80°,∠β=100°.
6. 互为余角的两个角之差为 35°,则较大角的补角度数是_______.
117.5°
针对训练
直线与角
几何图形
立体图形
平面图形
概念与性质
运算
直线、射线、线段
角
尺规作图
两点确定一条直线
两点之间线段最短
线段的中点
角平分线
互为余(补)角的概念与性质
线段(角)的和、差、倍、分
线段的和、差、倍、分计算
角的和、差、倍、分计算
度、分、秒的转化
小结与复习
第4章 几何图形初步
几何图形
立体图形
多面体、旋转体
两点间的距离
平面图形
线段的大小、比较、运算和画法
基本事实
直线、射线
线段
角
余角和补角
角的大小、比较、运算和画法
一、几何图形
1. 几何图形都是由点、线、面、体组成的.
2. 点、线、面、体之间的联系
(1) 体是由面围成,面与面相交成线,线与线相交成点;
(2) 点动成线、线动成面、面动成体.
(2)平面图形上的各点都在同一个平面内,如
3. 立体图形与平面图形
(1)立体图形上的点不都在同一个平面内,如
二、直线、射线、线段
1. 有关直线的基本事实
经过两点有一条直线,并且只有一条直线.
2. 直线、射线、线段的区别
类型 端点个数 延伸性 能否度量
线段
射线
直线
2 个
不能延伸
可度量
1 个
向一个方向
无限延伸
不可度量
无端点
向两个方向
无限延伸
不可度量
4. 有关线段的基本事实
两点之间线段最短
3. 线段的中点
应用格式:
A
C
B
因为 C 是线段 AB 的中点,
所以 AC = BC = AB,
AB = 2AC = 2BC.
5. 线段长短的比较方法
度量法或叠合法
三、角
1. 角的定义
(1) 从一个点出发的两条射线组成的图形,叫做角.
(2) 角也可以看做由一条射线绕着它的端点旋转所形成的图形.
2. 角的度量
度、分、秒的互化
1°=60′,1′=60″,
3. 角的大小的比较方法
度量法或叠合法
1″= ′,1′= °
4. 角的平分线
O
B
A
C
应用格式:
5. 余角与补角的性质
同角(等角)的补角相等
同角(等角)的与角相等
因为 OC 是∠AOB 的平分线,
所以∠AOC=∠BOC= ∠AOB,
∠AOB=2∠BOC=2∠AOC.
例1 如图所示,直线 l,线段 a,射线 OA,能相交的几组图形是 ( )
B
A. (1)(3)(4) B. (1)(4)(5) C. (1)(4)(6) D. (2)(3)(5)
(1)
(4) (5) (6)
(3)
(2)
考点一 线段、直线与射线
解析:此题相当于一条线段上有 3 个点,有多少种不同的票价即有多少条线段:4 + 3 + 2 + 1 = 10;有多少种车票是要考虑顺序的,则有 10×2 = 20.
1. 往返于甲、乙两地的火车中途要停靠三个站,则有______种不同的票价 (来回票价一样),需准备______种车票.
10
20
针对训练
例2 点 C 在线段 AB 所在的直线上,点 M,N 分别是 AC,BC 的中点.
(1) 如图,AC = 8 cm,CB = 6 cm,求线段 MN 的长;
A M C N B
所以 CM= AC=4 (cm),CN= BC=3 (cm).
解:因为点 M,N 分别是 AC,BC 的中点,
所以 MN=CM+CN=4+3=7 (cm).
考点二 线段长度的计算
(2) 若 C 为线段 AB 上任一点,满足 AC + CB = a cm,
其它条件不变,你能猜想 MN 的长度吗?并说明
理由;
A M C N B
理由:同(1)可得 CM = AC,CN = BC,
所以 MN = CM+CN = AC+ BC
= (AC+BC) = a (cm).
猜想:MN = a cm.
(3) 若C 在线段 AB的延长线上,且满足 AC-BC = b cm,
M,N 分别为 AC,BC 的中点,你能猜想 MN 的长
度吗?请画出图形,并说明理由.
A M B N C
MN = MC-NC = AC- BC
= (AC-BC) = b (cm).
猜想:MN = b cm.
理由:根据题意画出图形,由图可得
2. 已知:点 A,B,C 在一直线上,AB = 12 cm,BC =
4 cm. 点 M,N 分别是线段 AB,BC 的中点. 求线
段 MN 的长度.
A M C N B
图①
所以 BM = AB = ×12 = 6 (cm),
BN = BC = ×4 = 2 (cm).
解:如图①,当 C 在线段 AB 上时,
因为 M,N 分别是 AB,BC 的中点,
所以 MN = BM-BN = 6-2 = 4 (cm).
方法总结:无图条件下,注意多解情况要分类讨论,培养分类意识.
C
A
M
N
B
图②
所以 BM = AB = ×12 = 6 (cm),
BN = BC = ×4 = 2 (cm)
如图②,当 C 在线段 AB 外时,
因为 M,N 分别是 AB,BC 的中点,
所以 MN = BM + BN = 6 + 2 = 8 (cm).
考点三 角的度量及角度的计算
例3 45°52′48″=______°;
126.31°= ____°____′____″;
25°18′÷3=______;
126.31°=126°+0.31×60′=126°+18.6′
=126°18′+0.6×60″=126°18′36″.
解析:45°52′48″=45°+52′+(48÷60)′=45°+52.8′
=45°+(52.8÷60)°=45.88°.
25°18′÷3=8°+1°18′÷3=8°+78′÷3=8°26′.
45.88
126
18
36
8°26′
3. 若∠A=20°18′,∠B=20°15′30″,∠C=20.25°,则 ( )
A.∠A>∠B>∠C B.∠B>∠A>∠C
C.∠A>∠C>∠B D.∠C>∠A>∠B
A
4. 5 点整时,时钟上时针与分钟之间的夹角是 ( )
A. 210° B. 30° C. 150° D. 60°
C
针对训练
例4 如图,∠AOB 是直角,ON 是∠AOC 的平分线,OM 是∠BOC 的平分线.
(1) 当∠AOC = 50° 时,求∠MON 的大小;
O
B
M
A
N
C
提示:先求出∠BOC 的度数,再根据角平分线的定义求出∠COM,∠CON,然后根据∠MON =∠COM-∠CON
代入数据进行计算即可得解.
所以∠MON =∠COM-∠CON = 70°-25° = 45°.
解:因为∠AOB是直角,∠AOC = 50°, 所以∠BOC =∠AOB +∠AOC
= 90° + 50° = 140°.
因为 ON 是∠AOC 的平分线,
OM 是∠BOC 的平分线,
所以∠COM = ∠BOC = ×140° = 70°,
∠CON = ∠AOC = ×50° = 25°.
O
B
M
A
N
C
(2) 当∠AOC=α 时,∠MON 等于多少度?
O
B
M
A
N
C
所以∠MON =∠COM-∠CON = (90° + α)- α = 45°.
解:∠BOC =∠AOB +∠AOC = 90° + α.
因为 ON 是∠AOC 的平分线,
OM 是∠BOC 的平分线,
∠CON = ∠AOC = α.
所以∠COM = ∠BOC = (90° + α),
(3) 当锐角∠AOC 的大小发生改变时,∠MON 的大小
也会发生改变吗?为什么?
解:不会发生变化.
由 (2) 可知∠MON 的大小与∠AOC
无关,总是等于∠AOB 的一半.
O
B
M
A
N
C
5. 如图,长方形纸片 ABCD,点 E、F 分别在边 AB、CD 上,连接 EF.将∠BEF 对折,点 B 落在直线 EF 上的点 B' 处,得折痕 EM;将∠AEF 对折,点 A 落在直线 EF 上的点 A' 处,得折痕 EN,求∠NEM 的度数.
针对训练
解:由折纸过程可知, EM 平分∠BEB' ,EN 平分∠AEA'.
因为∠BEB'+∠AEA'=180°,
所以有∠NEM=∠NEA'+∠MEB'
所以有∠MEB'= ∠BEB',∠NEA'= ∠AEA'.
= (∠AEA'+∠BEB' ) =90°.
= ∠AEA'+ ∠BEB'
考点四 余角和补角
例5 已知∠α 和∠β 互为补角,并且∠β 的一半比∠α 小 30°,求∠α、∠β.
【解析】设∠α=x°,用 x 表示出∠β,列出方程即可.
解:设∠α=x°,则∠β=180°-x°.
根据题意 ∠β=2(∠α-30°),
即 180- x=2(x -30),
解得 x=80.
所以 ,∠α=80°,∠β=100°.
6. 互为余角的两个角之差为 35°,则较大角的补角度数是_______.
117.5°
针对训练
直线与角
几何图形
立体图形
平面图形
概念与性质
运算
直线、射线、线段
角
尺规作图
两点确定一条直线
两点之间线段最短
线段的中点
角平分线
互为余(补)角的概念与性质
线段(角)的和、差、倍、分
线段的和、差、倍、分计算
角的和、差、倍、分计算
度、分、秒的转化
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
