第5章 数据的收集与整理 小结与复习 课件(共24张PPT)
文档属性
| 名称 | 第5章 数据的收集与整理 小结与复习 课件(共24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-08 06:31:32 | ||
图片预览








文档简介
(共24张PPT)
七年级上册数学(沪科版)
小结与复习
第 5 章
数据的收集与整理
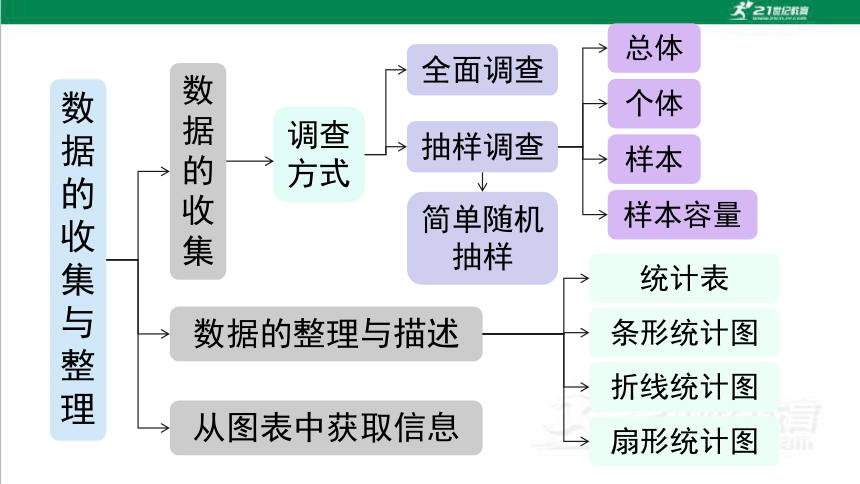
数据的收集与整理
数据的收集
数据的整理与描述
从图表中获取信息
调查方式
全面调查
抽样调查
简单随机抽样
总体
个体
样本
样本容量
统计表
条形统计图
折线统计图
扇形统计图
一、数据的收集
1. 调查是收集数据的重要方法,可分全面调查与抽样调查.
全面调查:对全体对象进行调查.
抽样调查:从被考察的全体对象中抽出一部分进行考察的调查方式.
2. 总体:所要考察对象的全体叫做总体.
个体:总体中的每一个考查对象叫做个体.
样本:从总体中抽取的一部分个体叫做总体的一个样本.
样本容量:样本中个体的数量叫做样本容量.
二、数据的整理
1. 数据的整理方式有统计表与统计图.
统计图包括条形统计图、折线统计图、扇形统计图.
2. 各类统计图描述数据时各具优势.
条形统计图:能清楚的表示出事物的绝对数量.
折线统计图:能清楚的反映事物的变化趋势.
扇形统计图:能清楚的表示各部分占总体的百分率.
(1)将数据分组整理,列出统计表;
(2)分别计算各部分在整体中所占的百分比;
(3)分别计算各部分相应的扇形圆心角的度数;
(4)用圆规画圆,再利用量角器画出各圆心角,从而把圆面按百分比分成若干个扇形;
(5)分别将各部分占整体的百分比以及相应的名称标注在扇形图上;并填写标题.
三、制作扇形统计图的步骤:
考点一 调查的方式
例1 下列调查:①调查本班同学的视力;②调查一批节能灯管的使用寿命;③为保证“嫦娥三号”的成功发射,对其零部件进行检查;④对乘坐某班次客车的乘客进行安检. 其中适合采用抽样调查的是 ( )
A. ① B. ② C. ③ D. ④
B
方法总结
下面的情形常采用抽样调查:
1. 当受客观条件限制,无法对所有个体进行普查时,如考查某市中学生的视力.
2. 当调查具有破坏性,不允许普查时,如考查某一批灯泡的使用寿命.
3. 当总体的容量较大,个体分布较广时,考查受多客观条件限制,宜用抽样调查.
针对训练
1. 下列采用的调查方式中,不合适的是( )
A. 为了了解全国中学生的身高状况,采用抽样调查的方式.
B. 班长要了解本班同学生日,采用普查的方式.
C. 医生要了解某病人体内含病毒的情况,需抽血进行化验,采用普查的方式.
D. 为了了解人们保护水资源的意识,采用抽样调查的方式.
C
考点二 总体、个体、样本、样本容量
例2 我市今年有 4 万名考生参加中考,为了了解这些考生的数学成绩,从中抽取了 2000 名考生的数学成绩进行统计分析,在这个问题中,下列说法:① 这 4 万名考生的数学中考成绩是总体;② 每名考生是个体;③ 2000 名考生是总体的一个样本;④ 样本容量为 2000. 其中说法正确的有 ( )
A. 4 个 B. 3 个 C. 2 个 D. 1 个
C
解析:①正确;②错误,个体应是每名考生的数学中考成绩;③错误,样本应是从中抽取的 2000名考生的数学中考成绩;④正确. 所以其中说法正确的共有 2 个,故选 C.
提示:在统计问题中,总体、个体和样本都是考查的对象,如学生的成绩,产品的质量等,样本容量是样本中所包含的个体数目.
针对训练
2. 某校要了解初三女生的身高,从初三 500 名女生中抽出 50 名进行测量,在这个问题中,总体、个体、样本、样本容量各指什么?
总体:500 名女生的身高;
个体:每一名女生的身高;
样本:抽取的 50 名女生的身高;
样本容量:50.
考点三 统计图的选择
例3 空气是由多种气体混合而成的,为了简明扼要的介绍空气的组成情况,较好的描述数据,最适合使用的统计图示 ( )
A. 扇形图 B. 条形图 C. 折线图 D. 以上均可以
提示:条形统计图:能清楚的表述出事物的绝对数量;
折线统计图:能清楚地反映事物的变化趋势;
扇形统计图:能清楚的表示各部分占总体的百分率.
A
针对训练
3. 要反映我市某一周每天最高气温的变化趋势,宜采用 ( )
A. 扇形图 B. 条形图 C. 折线图 D. 以上均可以
4. 许多电视台都有“模仿秀”“脱口秀”之类的娱乐节目,要比较选手的人气指数,现场大屏幕可以显示观众对选手的支持率,显示结果的时候通常选用( )
A. 扇形图 B. 条形图
C. 折线图 D. 以上均可以
C
B
考点四 统计图的综合应用
例4 为了推动课堂教学改革,打造高效课堂,配合我市“两型课堂”的课题研究,某中学对八年级部分学生就“分组合作学习”方
式的支持程度进行调查,
统计情况如图.
试根据题中提供的信息,回答下列问题:
(1) 求本次被调查的八年级学生的人数,并补全条形统计图.
(2) 若该校八年级学生共有 180
人,请你估计该校八年级有
多少名学生支持“分组合作
学习”方式(含“非常喜欢”
和“喜欢”两种情况的学生)?
分析:
(1) 用喜欢“分组合作学习”方式的圆心角度数和人数计算总人数从而求出非常喜欢“分组合作学习”方式的人数,补全条形统计图.
(2) 求出支持“分组合作学习”方式的人数所占的百分比,再求出人数.
解:(1)因为喜欢“分组合作学习”方式的圆心角度数为 120°,人数为 18,所以被调查的总人数为 (人).
故非常喜欢“分组合作学
习”方式的人数为
54 - 18 - 6 = 30(人),
补全条形统计图如下:
(2) 因为“非常喜欢”和“喜欢”两种情况在扇形统计图中所占圆心角为:120° + 200° = 320°,
所以支持“分组合作学习”方式所占百分比为 ×100%,
所以该校八年级 180 名学生中,有 180× ×100% = 160 名学生支持“分组合作学习”方式.
针对训练
5. 2022 年 12 月份,某市总工会组织该市各单位参加“迎新春长跑活动”,将报名的男运动员分成 3 组:青年组,中年组,老年组,各组人数所占比例如图所示,已知青年组有 120 人,则中年组
与老年组人数分别是 ( )
A. 30,10 B. 60,20
C. 50,30 D. 60,10
B
6. 某市每年都要举办中小学“三独”比赛 (包括独唱、独舞、独奏三个类别),如图是该市 2022 年参加“三独”比赛的不完整的参赛人数统计图.
(1) 该市参加“三独”比赛的总人数是______人,图中独唱所在扇形的圆心角的度数是______度,并把条形图补充完整.
解析:总人数 = 120÷30% = 400 (人),
独唱的人数 = 400 - 120 - 80 = 200 (人),
独唱所在扇形的圆心角的度数为:
400
180
解:估计今年全市获奖人数约有
(人) .
(2) 从这次参赛选手中随机抽取 20 人调查,其中有 9 人获奖,请你估算今年全市约有多少人获奖.
数据的收集与
整理
有关概念
应用
全面调查
抽样调查
总体
个体
样本
样本容量
条形统计图
折线统计图
扇形统计图
1. 选择合适的统计图描述数据;
2. 从图表中的数据获取信息
七年级上册数学(沪科版)
小结与复习
第 5 章
数据的收集与整理
数据的收集与整理
数据的收集
数据的整理与描述
从图表中获取信息
调查方式
全面调查
抽样调查
简单随机抽样
总体
个体
样本
样本容量
统计表
条形统计图
折线统计图
扇形统计图
一、数据的收集
1. 调查是收集数据的重要方法,可分全面调查与抽样调查.
全面调查:对全体对象进行调查.
抽样调查:从被考察的全体对象中抽出一部分进行考察的调查方式.
2. 总体:所要考察对象的全体叫做总体.
个体:总体中的每一个考查对象叫做个体.
样本:从总体中抽取的一部分个体叫做总体的一个样本.
样本容量:样本中个体的数量叫做样本容量.
二、数据的整理
1. 数据的整理方式有统计表与统计图.
统计图包括条形统计图、折线统计图、扇形统计图.
2. 各类统计图描述数据时各具优势.
条形统计图:能清楚的表示出事物的绝对数量.
折线统计图:能清楚的反映事物的变化趋势.
扇形统计图:能清楚的表示各部分占总体的百分率.
(1)将数据分组整理,列出统计表;
(2)分别计算各部分在整体中所占的百分比;
(3)分别计算各部分相应的扇形圆心角的度数;
(4)用圆规画圆,再利用量角器画出各圆心角,从而把圆面按百分比分成若干个扇形;
(5)分别将各部分占整体的百分比以及相应的名称标注在扇形图上;并填写标题.
三、制作扇形统计图的步骤:
考点一 调查的方式
例1 下列调查:①调查本班同学的视力;②调查一批节能灯管的使用寿命;③为保证“嫦娥三号”的成功发射,对其零部件进行检查;④对乘坐某班次客车的乘客进行安检. 其中适合采用抽样调查的是 ( )
A. ① B. ② C. ③ D. ④
B
方法总结
下面的情形常采用抽样调查:
1. 当受客观条件限制,无法对所有个体进行普查时,如考查某市中学生的视力.
2. 当调查具有破坏性,不允许普查时,如考查某一批灯泡的使用寿命.
3. 当总体的容量较大,个体分布较广时,考查受多客观条件限制,宜用抽样调查.
针对训练
1. 下列采用的调查方式中,不合适的是( )
A. 为了了解全国中学生的身高状况,采用抽样调查的方式.
B. 班长要了解本班同学生日,采用普查的方式.
C. 医生要了解某病人体内含病毒的情况,需抽血进行化验,采用普查的方式.
D. 为了了解人们保护水资源的意识,采用抽样调查的方式.
C
考点二 总体、个体、样本、样本容量
例2 我市今年有 4 万名考生参加中考,为了了解这些考生的数学成绩,从中抽取了 2000 名考生的数学成绩进行统计分析,在这个问题中,下列说法:① 这 4 万名考生的数学中考成绩是总体;② 每名考生是个体;③ 2000 名考生是总体的一个样本;④ 样本容量为 2000. 其中说法正确的有 ( )
A. 4 个 B. 3 个 C. 2 个 D. 1 个
C
解析:①正确;②错误,个体应是每名考生的数学中考成绩;③错误,样本应是从中抽取的 2000名考生的数学中考成绩;④正确. 所以其中说法正确的共有 2 个,故选 C.
提示:在统计问题中,总体、个体和样本都是考查的对象,如学生的成绩,产品的质量等,样本容量是样本中所包含的个体数目.
针对训练
2. 某校要了解初三女生的身高,从初三 500 名女生中抽出 50 名进行测量,在这个问题中,总体、个体、样本、样本容量各指什么?
总体:500 名女生的身高;
个体:每一名女生的身高;
样本:抽取的 50 名女生的身高;
样本容量:50.
考点三 统计图的选择
例3 空气是由多种气体混合而成的,为了简明扼要的介绍空气的组成情况,较好的描述数据,最适合使用的统计图示 ( )
A. 扇形图 B. 条形图 C. 折线图 D. 以上均可以
提示:条形统计图:能清楚的表述出事物的绝对数量;
折线统计图:能清楚地反映事物的变化趋势;
扇形统计图:能清楚的表示各部分占总体的百分率.
A
针对训练
3. 要反映我市某一周每天最高气温的变化趋势,宜采用 ( )
A. 扇形图 B. 条形图 C. 折线图 D. 以上均可以
4. 许多电视台都有“模仿秀”“脱口秀”之类的娱乐节目,要比较选手的人气指数,现场大屏幕可以显示观众对选手的支持率,显示结果的时候通常选用( )
A. 扇形图 B. 条形图
C. 折线图 D. 以上均可以
C
B
考点四 统计图的综合应用
例4 为了推动课堂教学改革,打造高效课堂,配合我市“两型课堂”的课题研究,某中学对八年级部分学生就“分组合作学习”方
式的支持程度进行调查,
统计情况如图.
试根据题中提供的信息,回答下列问题:
(1) 求本次被调查的八年级学生的人数,并补全条形统计图.
(2) 若该校八年级学生共有 180
人,请你估计该校八年级有
多少名学生支持“分组合作
学习”方式(含“非常喜欢”
和“喜欢”两种情况的学生)?
分析:
(1) 用喜欢“分组合作学习”方式的圆心角度数和人数计算总人数从而求出非常喜欢“分组合作学习”方式的人数,补全条形统计图.
(2) 求出支持“分组合作学习”方式的人数所占的百分比,再求出人数.
解:(1)因为喜欢“分组合作学习”方式的圆心角度数为 120°,人数为 18,所以被调查的总人数为 (人).
故非常喜欢“分组合作学
习”方式的人数为
54 - 18 - 6 = 30(人),
补全条形统计图如下:
(2) 因为“非常喜欢”和“喜欢”两种情况在扇形统计图中所占圆心角为:120° + 200° = 320°,
所以支持“分组合作学习”方式所占百分比为 ×100%,
所以该校八年级 180 名学生中,有 180× ×100% = 160 名学生支持“分组合作学习”方式.
针对训练
5. 2022 年 12 月份,某市总工会组织该市各单位参加“迎新春长跑活动”,将报名的男运动员分成 3 组:青年组,中年组,老年组,各组人数所占比例如图所示,已知青年组有 120 人,则中年组
与老年组人数分别是 ( )
A. 30,10 B. 60,20
C. 50,30 D. 60,10
B
6. 某市每年都要举办中小学“三独”比赛 (包括独唱、独舞、独奏三个类别),如图是该市 2022 年参加“三独”比赛的不完整的参赛人数统计图.
(1) 该市参加“三独”比赛的总人数是______人,图中独唱所在扇形的圆心角的度数是______度,并把条形图补充完整.
解析:总人数 = 120÷30% = 400 (人),
独唱的人数 = 400 - 120 - 80 = 200 (人),
独唱所在扇形的圆心角的度数为:
400
180
解:估计今年全市获奖人数约有
(人) .
(2) 从这次参赛选手中随机抽取 20 人调查,其中有 9 人获奖,请你估算今年全市约有多少人获奖.
数据的收集与
整理
有关概念
应用
全面调查
抽样调查
总体
个体
样本
样本容量
条形统计图
折线统计图
扇形统计图
1. 选择合适的统计图描述数据;
2. 从图表中的数据获取信息
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
