期末测试卷二(含答案)2024-2025学年人教版数学七年级下册
文档属性
| 名称 | 期末测试卷二(含答案)2024-2025学年人教版数学七年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 224.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-08 09:20:40 | ||
图片预览



文档简介
2024-2025学年七年级下册第期末测试卷二(数学)
题号 一 二 三 四 五 总分
得分
一 、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有 一项是符合题目要求的.
1.下列实数中是无理数的为 ( )
A.-3.14 B.0 C. D.
2.如图,点M 到直线l的距离是 A. 线 段MA的长度 B. 线 段MB 的长度 C.线 段MC 的长度 D. 线 段MD 的长度 ( )
3.估计 的大小在 ( )
A.5 与 6 之 间 B.4 与 5 之 间
C.3 与 4 之 间 D.2 与 3 之 间
4.空气由多种气体混合而成,为了直观介绍空气中各成分的百分比,最适合使用的统计
图 是
A. 条形图 B. 折线图
5. 如 果a>b, 那么下列运算正确的是
A.a-3C.3a<3b
6. 已知 |x+y+1|+ √2x-y=0, 则 x-y 的值为
(
B.-1
)A
C. 直方图
B.a+3D
( )
D. 扇形图
( )
( )
D.1
7.植树节这天有20名同学种了52棵树苗,其中男生每人种树3棵,女生每人种树2棵. 设男生有x 人,女生有y 人,根据题意,下列方程组正确的是 ( )
B. C D.
8.如图,点A,B 的坐标分别为(2,0),(0,1),将线段AB 平移得到A B , 则 a+b 的值 为 ( ) A.2 B.3 C.4 D.5
y↑
B (a,2)
B(0,1) A (3,b)
0 A(2,0) X
第8题图 第9题图
9. 如图,已知∠ FED+∠BGF=180°,∠B=∠D,∠FED-∠AED=55°,∠FED-∠BEF=
65°,则∠BCF 的度数为 ( ) A.50° B.47° C.45° D.40°
10.若关于x 的不等式组 仅有四个整数解,则a 的取值范围是 ( )
A. B
D
二、填空题:本大题共5小题,每小题3分,共15分.
11.若 x =81, 则 x=
12.将一副三角板(∠A=30°,∠E=45°) 按如图所示方式摆放,使AB//EF, 则∠1= °.
13.为了估计湖中有多少条鱼,先从湖中捕捉50条鱼做记号,然后放回湖里,经过一段时 间,等带记号的鱼完全混于鱼群中之后再捕捞,第二次捕鱼共20条,有10条做了记 号,则估计湖里有 条鱼.
14.某运输公司要将300t 的货物运往某地,现有A,B 两种型号的汽车可调用,已知 A 型 汽车每辆可装货物20t,B 型汽车每辆可装货物15t. 在每辆汽车不超载的情况下,要 把这300t 货物一次性装运完成,并且 A 型汽车确定要用7辆,至少调用 B 型汽车的 辆数为
15.在平面直角坐标系中,对于点P(x,y), 我们把点P'(-y+1,x+1) 叫作点P 的伴随点. 已知点A 的伴随点为A ,点 A 的伴随点为A ,点 A 的伴随点为A ,…, 这样依次得 到点A ,A ,A , … ,An, … . 若点A 的坐标为(2,4),则点A 024的坐标为
三、解答题(一):本大题共3小题,每小题7分,共21分.
16.计算: |-3|+(-1)2024— +.
17.解不等式组:
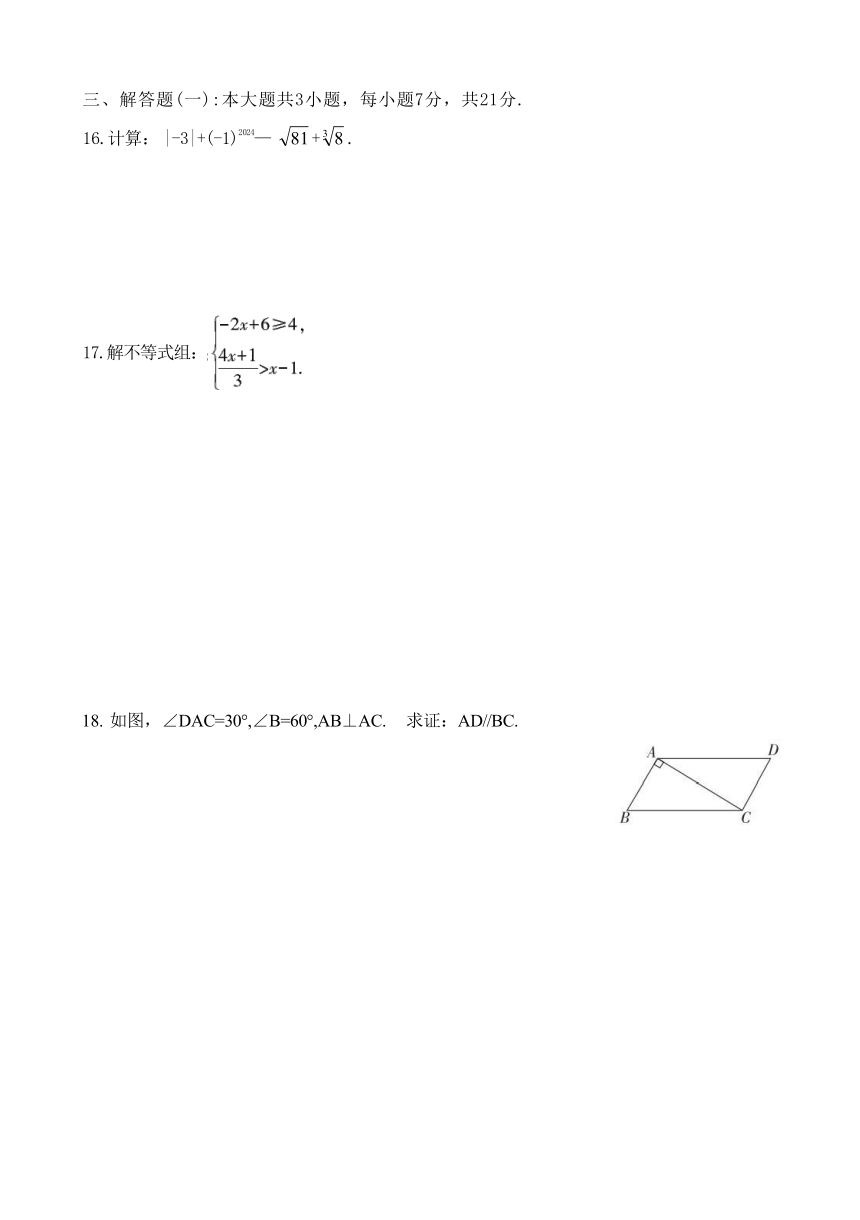
18. 如图,∠DAC=30°,∠B=60°,AB⊥AC. 求证:AD//BC.
四、解答题(二):本大题共3小题,每小题9分,共27分.
19.学生对某小区居民的健身方式进行调查,并将调查结果绘制成如图两幅不完整的统 计图.
快走
跳舞
36%
球类 太极 跑步
图① 图②
请根据所给信息解答下列问题:
(1)本次共调查 人;
(2)补全图①中的条形统计图,图②中“跑步”所在扇形的圆心角度数是 ;
(3)估计该小区居民2000人中喜欢太极的有多少人
20.在解方程时,由于粗心,甲看错了方程组中的a, 解 乙看错了 方程组中的b,解得
(1)甲把a 看成了什么,乙把b 看成了什么
(2)求出原方程组的正确解.
21.某汽车销售公司经销某品牌A,B 两款汽车,今年1,2月销售情况如下表所示:(A,B 两款汽车的销售单价保持不变)
月份 销售数量/辆 销售金额/万元
A款 B款
1 月 3 1 35
2 月 1 3 33
(1)A,B 两款汽车每辆的售价分别为多少万元
(2)若A 款汽车每辆进价为8万元,B 款汽车每辆进价为6万元,公司预计用不多于 105万元且不少于99万元的资金购进这两款汽车共15辆,求出所有的进货方案.
五、解答题(三):本大题共2小题,第22题13分,第23题14分,共27分.
22.如图,A(-1,0),C(1,4), 点 B 在 x 轴上,且AB=3.
(1)求点B 的坐标.
(2)求三角形 ABC的面积.
(3)在y 轴上是否存在点P,使以A,B,P 三点为顶点的三角形的面积为10 若存在, 请求出点P 的坐标;若不存在,请说明理由.
23.已 知AM//CN,点 B 为平面内一点,AB⊥BC 于点B.
(1)如图①,如果∠A=40°, 那么∠C 等于 度.
(2)如图②,过点B 作 BD⊥AM 于点D,探究∠DAB 与∠C 之间的数量关系,并说明理由.
(3)如图③,在(2)问的条件下,点E,F 在 DM 上,连接 BE,BF,CF, 若 BE 平 分 ∠ABD,BF 平分∠DBC,∠FCB+∠NCF=180°,∠BFC=3∠DBE, 求∠EBC 的度数.
图① 图② 图③
期末质量检测卷(二)
1.C 2.B 3.B 4.D 5.D 6.A 7.A 8.A 9.C
10.B 11.±9 12.105 13.100 14.11 15.(3,-1)
16.解:原式=3+1-9+2=-3.
17.解 :
解不等式①,得x≤1.
解不等式②,得x>-4.
∴原不等式组的解集为-418. 证明:∵AB⊥AC, ∠BAC=90° .
∵∠B=60°, ∴∠ACB=180°-∠BAC-∠B=30°. ∵∠DAC=30°, ∴∠DAC=∠ACB. ∴AD//BC.
19.解:(1)50
(2)36°
补全条形统计图如图①所示.
图①
(3)2
答:估计该小区居民2000人中喜欢太极的有120人.
20.解:(1)将’代入原方程组,得 解得
代入原方程组,得 解得
∴甲把a 看成乙把b 看成
(2)由(1)可知原方程组中a=-1,b=10.
∴原方程组为解得
21.解:(1)设A 款汽车每辆的售价为x 万元,B 款汽车每辆 的售价为y 万元.
依题意,得解得
答:A 款汽车每辆的售价为9万元,B 款汽车每辆的售 价为8万元.
(2)设购进m 辆 A款汽车,则购进(15-m)辆 B 款汽车.
依题意,得 ·’解得- ∵m 为整数,∴ m 可以为5,6,7.
∴该公司共有3种进货方案.
方案1:购进5辆A 款汽车,10辆B 款汽车;
方案2:购进6辆A 款汽车,9辆B 款汽车;
方案3:购进7辆A 款汽车,8辆B 款汽车.
22.解:(1)当点B 在点A 的右边时,-1+3=2; 当点B 在点A 的左边时,-1-3=-4.
∴ 点B 的坐标为(2,0)或(-4,0).
(2)三角形ABC的 面 积
(3)存在.设点P 到x 轴的距离为h. 由题意,得 .解得
当点P 在 y 轴正半轴时,
当点P 在 y 轴负半轴时,
综上所述,点P 的坐标为 或
23.解:(1)50
(2)∠DAB+∠C=90°. 理由如下:
如图②,过点B 作 BG//AM. ∵AM//CN,
∴BG//AM//CN.
∴∠DAB=∠ABG,∠C=∠CBG.
∵AB⊥BC,
∴∠ABC=90°.
∴∠ABG+∠CBG=90°.
∴∠DAB+∠C=90°.
(3)如图③,作 BH//AM.
∵AM//CN,
∴BH//AM//CN.
∵BE 平分∠ ABD,BF 平分∠ DBC, ∴设∠ DBE=∠ABE=x,∠AFB=y, 则∠ABD=2x,∠HBF=∠AFB=y, ∠BFC=3∠DBE=3x,
∠DBF=90°-y.
∴∠AFC=3x+y,∠CBF=∠DBF=90°-y.
∵∠AFC+∠NCF=180°,∠FCB+∠NCF=180°, ∴∠FCB=∠AFC=3x+y.
在三角形 BCF 中,∠ CBF+∠BFC+∠FCB=180.o ∴90°-y+3x+3x+y=180° .
∴x=15° .
∵AB⊥BC,
∴∠ABC=90°.
∴∠EBC=15°+90°=105° .
题号 一 二 三 四 五 总分
得分
一 、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有 一项是符合题目要求的.
1.下列实数中是无理数的为 ( )
A.-3.14 B.0 C. D.
2.如图,点M 到直线l的距离是 A. 线 段MA的长度 B. 线 段MB 的长度 C.线 段MC 的长度 D. 线 段MD 的长度 ( )
3.估计 的大小在 ( )
A.5 与 6 之 间 B.4 与 5 之 间
C.3 与 4 之 间 D.2 与 3 之 间
4.空气由多种气体混合而成,为了直观介绍空气中各成分的百分比,最适合使用的统计
图 是
A. 条形图 B. 折线图
5. 如 果a>b, 那么下列运算正确的是
A.a-3
6. 已知 |x+y+1|+ √2x-y=0, 则 x-y 的值为
(
B.-1
)A
C. 直方图
B.a+3
( )
D. 扇形图
( )
( )
D.1
7.植树节这天有20名同学种了52棵树苗,其中男生每人种树3棵,女生每人种树2棵. 设男生有x 人,女生有y 人,根据题意,下列方程组正确的是 ( )
B. C D.
8.如图,点A,B 的坐标分别为(2,0),(0,1),将线段AB 平移得到A B , 则 a+b 的值 为 ( ) A.2 B.3 C.4 D.5
y↑
B (a,2)
B(0,1) A (3,b)
0 A(2,0) X
第8题图 第9题图
9. 如图,已知∠ FED+∠BGF=180°,∠B=∠D,∠FED-∠AED=55°,∠FED-∠BEF=
65°,则∠BCF 的度数为 ( ) A.50° B.47° C.45° D.40°
10.若关于x 的不等式组 仅有四个整数解,则a 的取值范围是 ( )
A. B
D
二、填空题:本大题共5小题,每小题3分,共15分.
11.若 x =81, 则 x=
12.将一副三角板(∠A=30°,∠E=45°) 按如图所示方式摆放,使AB//EF, 则∠1= °.
13.为了估计湖中有多少条鱼,先从湖中捕捉50条鱼做记号,然后放回湖里,经过一段时 间,等带记号的鱼完全混于鱼群中之后再捕捞,第二次捕鱼共20条,有10条做了记 号,则估计湖里有 条鱼.
14.某运输公司要将300t 的货物运往某地,现有A,B 两种型号的汽车可调用,已知 A 型 汽车每辆可装货物20t,B 型汽车每辆可装货物15t. 在每辆汽车不超载的情况下,要 把这300t 货物一次性装运完成,并且 A 型汽车确定要用7辆,至少调用 B 型汽车的 辆数为
15.在平面直角坐标系中,对于点P(x,y), 我们把点P'(-y+1,x+1) 叫作点P 的伴随点. 已知点A 的伴随点为A ,点 A 的伴随点为A ,点 A 的伴随点为A ,…, 这样依次得 到点A ,A ,A , … ,An, … . 若点A 的坐标为(2,4),则点A 024的坐标为
三、解答题(一):本大题共3小题,每小题7分,共21分.
16.计算: |-3|+(-1)2024— +.
17.解不等式组:
18. 如图,∠DAC=30°,∠B=60°,AB⊥AC. 求证:AD//BC.
四、解答题(二):本大题共3小题,每小题9分,共27分.
19.学生对某小区居民的健身方式进行调查,并将调查结果绘制成如图两幅不完整的统 计图.
快走
跳舞
36%
球类 太极 跑步
图① 图②
请根据所给信息解答下列问题:
(1)本次共调查 人;
(2)补全图①中的条形统计图,图②中“跑步”所在扇形的圆心角度数是 ;
(3)估计该小区居民2000人中喜欢太极的有多少人
20.在解方程时,由于粗心,甲看错了方程组中的a, 解 乙看错了 方程组中的b,解得
(1)甲把a 看成了什么,乙把b 看成了什么
(2)求出原方程组的正确解.
21.某汽车销售公司经销某品牌A,B 两款汽车,今年1,2月销售情况如下表所示:(A,B 两款汽车的销售单价保持不变)
月份 销售数量/辆 销售金额/万元
A款 B款
1 月 3 1 35
2 月 1 3 33
(1)A,B 两款汽车每辆的售价分别为多少万元
(2)若A 款汽车每辆进价为8万元,B 款汽车每辆进价为6万元,公司预计用不多于 105万元且不少于99万元的资金购进这两款汽车共15辆,求出所有的进货方案.
五、解答题(三):本大题共2小题,第22题13分,第23题14分,共27分.
22.如图,A(-1,0),C(1,4), 点 B 在 x 轴上,且AB=3.
(1)求点B 的坐标.
(2)求三角形 ABC的面积.
(3)在y 轴上是否存在点P,使以A,B,P 三点为顶点的三角形的面积为10 若存在, 请求出点P 的坐标;若不存在,请说明理由.
23.已 知AM//CN,点 B 为平面内一点,AB⊥BC 于点B.
(1)如图①,如果∠A=40°, 那么∠C 等于 度.
(2)如图②,过点B 作 BD⊥AM 于点D,探究∠DAB 与∠C 之间的数量关系,并说明理由.
(3)如图③,在(2)问的条件下,点E,F 在 DM 上,连接 BE,BF,CF, 若 BE 平 分 ∠ABD,BF 平分∠DBC,∠FCB+∠NCF=180°,∠BFC=3∠DBE, 求∠EBC 的度数.
图① 图② 图③
期末质量检测卷(二)
1.C 2.B 3.B 4.D 5.D 6.A 7.A 8.A 9.C
10.B 11.±9 12.105 13.100 14.11 15.(3,-1)
16.解:原式=3+1-9+2=-3.
17.解 :
解不等式①,得x≤1.
解不等式②,得x>-4.
∴原不等式组的解集为-4
∵∠B=60°, ∴∠ACB=180°-∠BAC-∠B=30°. ∵∠DAC=30°, ∴∠DAC=∠ACB. ∴AD//BC.
19.解:(1)50
(2)36°
补全条形统计图如图①所示.
图①
(3)2
答:估计该小区居民2000人中喜欢太极的有120人.
20.解:(1)将’代入原方程组,得 解得
代入原方程组,得 解得
∴甲把a 看成乙把b 看成
(2)由(1)可知原方程组中a=-1,b=10.
∴原方程组为解得
21.解:(1)设A 款汽车每辆的售价为x 万元,B 款汽车每辆 的售价为y 万元.
依题意,得解得
答:A 款汽车每辆的售价为9万元,B 款汽车每辆的售 价为8万元.
(2)设购进m 辆 A款汽车,则购进(15-m)辆 B 款汽车.
依题意,得 ·’解得- ∵m 为整数,∴ m 可以为5,6,7.
∴该公司共有3种进货方案.
方案1:购进5辆A 款汽车,10辆B 款汽车;
方案2:购进6辆A 款汽车,9辆B 款汽车;
方案3:购进7辆A 款汽车,8辆B 款汽车.
22.解:(1)当点B 在点A 的右边时,-1+3=2; 当点B 在点A 的左边时,-1-3=-4.
∴ 点B 的坐标为(2,0)或(-4,0).
(2)三角形ABC的 面 积
(3)存在.设点P 到x 轴的距离为h. 由题意,得 .解得
当点P 在 y 轴正半轴时,
当点P 在 y 轴负半轴时,
综上所述,点P 的坐标为 或
23.解:(1)50
(2)∠DAB+∠C=90°. 理由如下:
如图②,过点B 作 BG//AM. ∵AM//CN,
∴BG//AM//CN.
∴∠DAB=∠ABG,∠C=∠CBG.
∵AB⊥BC,
∴∠ABC=90°.
∴∠ABG+∠CBG=90°.
∴∠DAB+∠C=90°.
(3)如图③,作 BH//AM.
∵AM//CN,
∴BH//AM//CN.
∵BE 平分∠ ABD,BF 平分∠ DBC, ∴设∠ DBE=∠ABE=x,∠AFB=y, 则∠ABD=2x,∠HBF=∠AFB=y, ∠BFC=3∠DBE=3x,
∠DBF=90°-y.
∴∠AFC=3x+y,∠CBF=∠DBF=90°-y.
∵∠AFC+∠NCF=180°,∠FCB+∠NCF=180°, ∴∠FCB=∠AFC=3x+y.
在三角形 BCF 中,∠ CBF+∠BFC+∠FCB=180.o ∴90°-y+3x+3x+y=180° .
∴x=15° .
∵AB⊥BC,
∴∠ABC=90°.
∴∠EBC=15°+90°=105° .
同课章节目录
