北京市第二中学2024?2025学年高一下学期第五学段数学试题(含详解)
文档属性
| 名称 | 北京市第二中学2024?2025学年高一下学期第五学段数学试题(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-09 00:33:52 | ||
图片预览




文档简介
北京市第二中学2024 2025学年高一下学期第五学段数学试题
一、单选题
1.已知,是两条不同的直线,,是两个不同的平面,则下列命题正确的是( )
A.若,,,则 B.若,,则
C.若,,,则 D.若,,,则
2.设长方体的长、宽、高分别为,其顶点都在一个球面上,则该球的体积为( )
A. B. C. D.
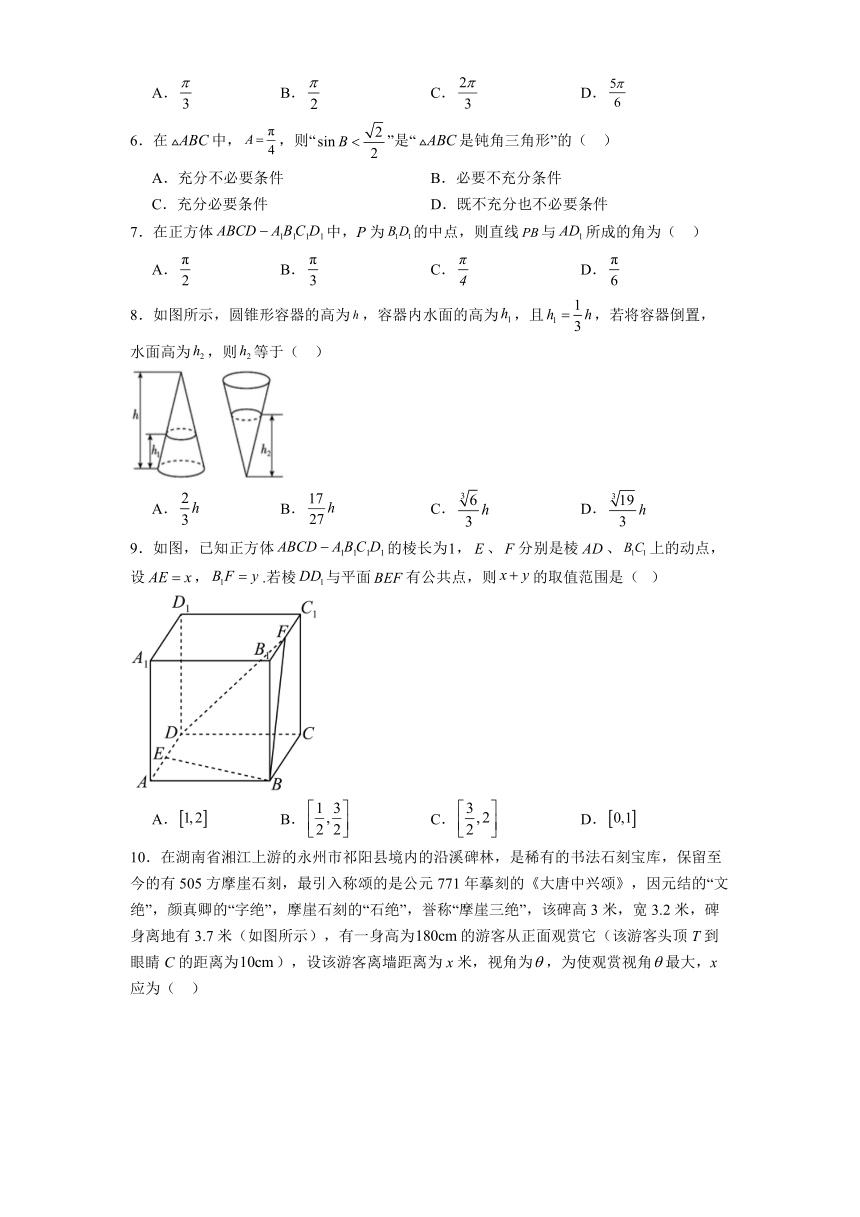
3.如图,点A,B,C,M,N为正方体的顶点或所在棱的中点,则下列各图中,不满足直线平面的是( )
A. B. C. D.
4.如图所示,为的直观图,且的面积为,则中最长的边长为( )
A. B.
C. D.
5.已知单位向量满足,则与的夹角为( )
A. B. C. D.
6.在中,,则“”是“是钝角三角形”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
7.在正方体中,P为的中点,则直线与所成的角为( )
A. B. C. D.
8.如图所示,圆锥形容器的高为,容器内水面的高为,且,若将容器倒置,水面高为,则等于( )
A. B. C. D.
9.如图,已知正方体的棱长为,、分别是棱、上的动点,设,.若棱与平面有公共点,则的取值范围是( )
A. B. C. D.
10.在湖南省湘江上游的永州市祁阳县境内的沿溪碑林,是稀有的书法石刻宝库,保留至今的有505方摩崖石刻,最引入称颂的是公元771年摹刻的《大唐中兴颂》,因元结的“文绝”,颜真卿的“字绝”,摩崖石刻的“石绝”,誉称“摩崖三绝”,该碑高3米,宽3.2米,碑身离地有3.7米(如图所示),有一身高为的游客从正面观赏它(该游客头顶T到眼睛C的距离为),设该游客离墙距离为x米,视角为,为使观赏视角最大,x应为( )
A. B.3 C. D.
11.如图所示,将一副三角板拼成平面四边形,将等腰直角沿向上翻折,得到,设,点分别为棱的中点,为线段上的动点,下列说法错误的是( )
A.在翻折过程中,存在某个位置使得
B.若,则与平面所成角的正切值为
C.三棱锥体积的最大值为
D.当时,的最小值为
12.在单位正方体内任取一个点,过这个点作三个平行于正方体面的平面,将正方体分成个小长方体,则这些小长方体中体积不大于的长方体的个数的最小值是( )
A. B. C. D.
二、填空题
13.在正方体中,二面角的平面角等于 .
14.已知向量.若,则 .
15.已知圆锥的侧面积为,且它的侧面展开图是一个半圆,则这个圆锥的底面半径是 .
16.如图,在正方体中,是棱的中点,记平面与平面的交线为,平面与平面的交线为,若直线分别与,所成的角为 , ,则 , .
17.已知正四面体中,分别在棱上. 若, ,则 .
18.球面三角学是研究球面三角形的边、角关系的一门学科.如图,球的半径为R,A,B,为球面上三点,劣弧BC的弧长记为,设表示以为圆心,且过B,C的圆,同理,圆的劣弧的弧长分别记为,曲面(阴影部分)叫做曲面三角形,,则称其为曲面等边三角形,线段OA,OB,OC与曲面围成的封闭几何体叫做球面三棱锥,记为球面.设.
①若平面是面积为的等边三角形,则;
②若,则;
③若平面为直角三角形,且,则;
④若,则球面的体积;
其中所有正确结论的序号是 .
三、解答题
19.已知函数.
(1)求的最小正周期和单调递增区间;
(2)若,求的最大值和最小值及取得最值时相应的值.
20.如图,在四棱锥中,底面为矩形,平面平面,,,、分别为、的中点.
(Ⅰ)求证:;
(Ⅱ)求证:平面平面;
(Ⅲ)求证:平面.
21.已知的面积为,再从条件①、条件②这两个条件中选择一个作为已知,求:
(1)和的值;
(2)的值.
条件①:,;条件②:,.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
22.如图所示,在三棱柱中,侧棱底面,为棱的中点.,, .
(1)求证:平面;
(2)求证:平面;
(3)在棱上是否存在点,使得平面平面?如果存在,求此时的值;如果不存在,请说明理由.
23.对于n行n列()的数表,定义T变换:任选一组,其中,,对于A中第行和第j列个数,将每个数同时加1,或者将每个数同时减1,其余的数不变,得到一个新数表.
(1)已知对依次进行4次T变换,如下:,写出a,b,c,d的值.
(2)已知,,那么是否可以依次进行有限次T变换,将A变换为B?说明理由.
(3)已知11行11列的数表,那么是否可以依次进行k次T变换,将其变换为?若可以,求k的最小值;若不可以,说明理由.
参考答案
1.【答案】D
【详解】
如图,在正方体中分析选项A、B、C.
A.平面,平面,平面平面,但,A错误.
B.,平面,但平面,B错误.
C.平面平面,平面,,但平面,C错误.
D.取直线的方向向量,直线的方向向量,
∵,,∴分别为平面的法向量,
∵,∴,∴,D正确.
故选D.
2.【答案】B
【详解】由题可知球直径为长方体的体对角线,故半径为,
.
故选B.
3.【答案】D
【详解】对于A,如下图所示,
易得,
则,
又平面,平面,
则平面,故A满足;
对于B,如下图所示,
为所在棱的中点,连接,
易得,
则四边形为平行四边形,
四点共面,
又易知,
又平面,平面,
则平面,故B满足;
对于C,如下图所示,
点为所在棱的中点,连接,
易得四边形为平行四边形,四点共面,
且,
又平面,平面,
则平面,故C满足;
对于D,连接,
由条件及正方体的性质可知四边形是等腰梯形,
所以与所在的直线相交,
故不能推出与平面不平行,故D不满足,
故选D.
4.【答案】B
【详解】设,
由题意可得,则,
所以,
所以在中,,
由,所以,即中最长的边长为.
故选B
5.【答案】C
【详解】化简得,
,
,,
,
故选:C.
6.【答案】A
【分析】先判断如果能不能推出是钝角三角形,再判断如果是钝角三角形,是否一定有即可.
【详解】如果,由于B是三角形的内角,并且,则,
即,是钝角三角形,
所以“”是“是钝角三角形”的充分条件;
如果是钝角三角形,不妨设,则,
所以“”不是“是钝角三角形”的必要条件.
故选A.
【方法总结】充分必要条件和对应集合的关系可根据如下规则转化:
若p是q的必要不充分条件,则q对应集合是p对应集合的真子集;
若p是q的充分不必要条件,则p对应集合是q对应集合的真子集;
(3)若p是q的充要条件,则p对应集合与q对应集合相等;
(4)若p是q的既不充分也不必要条件,则q对应集合与p对应集合互不包含.
7.【答案】D
【详解】如图,连接,因为∥,
所以或其补角为直线与所成的角,
因为平面,所以,又,,
所以平面,所以,
设正方体棱长为2,则,
,所以.
故选D
8.【答案】D
【详解】设容器底面半径为,倒置前液面的半径为,倒置后液面的半径为
则,
则水的体积为,
倒置后水的体积,
所以,
故选D
9.【答案】A
【详解】由题意,若,则棱与平面交于点,符合题意,此时;
若,,则棱与平面交于线段,符合题意,此时.
排除B、C、D选项.
故选A.
10.【答案】A
【详解】设,由图可知,
,
由基本不等式知,当,即时,最大,从而角最大.
故选A
11.【答案】D
【详解】对于A,当平面与平面垂直时,
,平面与平面的交线为,平面,
平面,又平面,
,,故A正确;
对于B,连接,
因为平面,
所以平面,
又平面,所以,
因为为的中点,
所以,
又平面,
所以平面,
则即为与平面所成角的平面角,
在中,,则,
,
所以,
即与平面所成角的正切值为,故B正确;
对于C,三棱锥的体积(为点到平面的距离).
.
当平面平面时,最大,的最大值为,此时,所以三棱锥体积的最大值为,选项C正确.
对于D,当时,因为为的中点,
所以,则,
又因为的中点,所以,
又,所以,
所以,
如图将沿旋转,使其与在同一平面内,
则当三点共线时,最小,
即的最小值为,
在中,,
则,
所以,
所以的最小值为,故D错误.
故选D.
12.【答案】B
【详解】设该正方体的长宽高分别被切成长度为和,和,和的两段,
设,且根据据对称性,可不妨设,
此时,8个长方体的体积分别是
由,可知,
因为,
所以,
又因为,
所以和中至少有一个数不超过,
所以这8个长方体中至少有4个的体积不超过.
当时,8个长方体的体积分别是0.0625;0.061875;0.061875;0.075625;0.151875;0.185625;0.185625;0.226875;
此时这8个长方体中恰有4个的体积不超过.
综上,这些小长方体中体积不大于的长方体个数的最小值为4.
故选:B.
13.【答案】
【详解】
在正方体中,面,面,
所以,因为,,平面,
所以平面,平面,所以,
所以二面角的平面角为,在正方体中易知.
14.【答案】.
【详解】,
,解得.
15.【答案】1
【详解】设圆锥的底面半径为r,圆锥的母线长为l,则,解得:,又,解得:.
16.【答案】;
【解析】本题考查等角定理及其辨析、面面平行
在正方体中,是棱的中点,
如图,延长与延长线交于点,连接,则直线即为直线,,
由,得,又,于是,
由平面平面,平面 平面,平面 平面,
则,又,因此,,
所以.
17.【答案】3或
【详解】
当时,是等边三角形,因此.
在中,由余弦定理可得,
则,解得.
当时,不妨设.
在中分别使用余弦定理可得
由可知是关于的方程的两个相异正实根,
所以
可写为,因此,解得.
即.
18.【答案】①②④
【详解】对于①,因等边三角形的面积为,则,
又,故,则,故①正确;
对于②,由可得,故,即②正确;
对于③,由余弦定理可知,由可得,,
即,化简得,.
取,则,则,故③错误;
对于④,由可得,故,
由正弦定理,的外接圆半径为,点到平面ABC的距离,
则三棱锥的体积,
而球面的体积,故④正确.
19.【答案】(1)最小正周期为,增区间为
(2)当时,,当时,
【详解】(1)函数
,
所以函数的最小正周期为,
由可得,
所以函数的增区间为.
(2)当时,,
故当时,即当时,取最小值,即;
当时,即当时,取最大值,即.
20.【答案】(Ⅰ)见解析;(Ⅱ)见解析;(Ⅲ)见解析.
【详解】(Ⅰ)∵,且为的中点,∴.
∵底面为矩形,∴,∴;
(Ⅱ)∵底面为矩形,∴.
∵平面平面,平面平面,平面,
∴平面,又平面,∴.
又,,、平面,平面,
∵平面,∴平面平面;
(Ⅲ)如图,取中点,连接.
∵分别为和的中点,∴,且.
∵四边形为矩形,且为的中点,∴,
∴,且,∴四边形为平行四边形,
∴,又平面,平面,∴平面.
21.【答案】(1)条件选择,答案见解析;
(2)条件选择,答案见解析.
【详解】(1)选①,在中,由得:,而,
则面积,解得,
由余弦定理得:,
所以,.
选②,在中,由得:,而,即,
则面积,解得,
由余弦定理得:,
所以,.
(2)选①,由(1)及正弦定理得:,则,
,而角为钝角,于是得,
所以.
选②,由(1)知,,
所以.
22.【答案】(1)证明见解析;
(2)证明见解析;
(3)存在,.
【详解】(1)连结交于O,连结
在中,因为M,O分别为AC,中点,所以
又因为平面,平面,所以平面
(2)因为侧棱底面ABC,平面ABC,所以
又M为棱AC中点,,所以
因为,,平面
所以平面,平面,所以
因为M为棱AC中点,,所以,又,
所以在和中,
所以,即,所以
因为,BM,平面,所以平面
(3)当点N为中点时,即,平面平面
设中点为D,连结DM,
因为D,M分别为,AC中点,所以,且
又因为N为中点,所以,且,
所以四边形DMBN是平行四边形,所以,
结合(2)平面,则平面,
又平面,所以平面平面
23.【答案】(1),
(2)不可以,理由见解析
(3)可以,k的最小值为400
【详解】(1)经过变换得到,显然没有变,从1变为2,
所以和均增加1,故,
经过变换得到,显然没有变,从1变为2,
故和均增加1,故,
经过变换得到,满足要求,
综上,,;
(2)不可以,理由如下:
由题可知,每次变换,数表中的所有数的和增加或减少5,
因为中所有数的和为0,所以经过有限次T变换后,各数之和应为5的倍数,
而中所有数的和为9,不合要求,
故不可以依次进行有限次T变换,将A变换为B.
(3)可以,且的最小值为400,
当所选时,所有加1的变换与减1的变换次数之差设为,
当所选且,或者且时,
所有加1的变换与减1的变换次数之差设为,
当所选时,加1的变换与减1的变换次数之差设为,
由于,
由于,,和为100,故,
由于或时,,和为,
故,
由于,故,
联立可得,解得,
所以,
其中符合题意的400次变换构造如下:
当所选时,各进行一次减1的变换,共进行100次变换,得到
当所选且,或者且时,
各进行10次加1的变换,共进行200次变换,得到
当所选时,进行100次减1的变换,得到
一、单选题
1.已知,是两条不同的直线,,是两个不同的平面,则下列命题正确的是( )
A.若,,,则 B.若,,则
C.若,,,则 D.若,,,则
2.设长方体的长、宽、高分别为,其顶点都在一个球面上,则该球的体积为( )
A. B. C. D.
3.如图,点A,B,C,M,N为正方体的顶点或所在棱的中点,则下列各图中,不满足直线平面的是( )
A. B. C. D.
4.如图所示,为的直观图,且的面积为,则中最长的边长为( )
A. B.
C. D.
5.已知单位向量满足,则与的夹角为( )
A. B. C. D.
6.在中,,则“”是“是钝角三角形”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
7.在正方体中,P为的中点,则直线与所成的角为( )
A. B. C. D.
8.如图所示,圆锥形容器的高为,容器内水面的高为,且,若将容器倒置,水面高为,则等于( )
A. B. C. D.
9.如图,已知正方体的棱长为,、分别是棱、上的动点,设,.若棱与平面有公共点,则的取值范围是( )
A. B. C. D.
10.在湖南省湘江上游的永州市祁阳县境内的沿溪碑林,是稀有的书法石刻宝库,保留至今的有505方摩崖石刻,最引入称颂的是公元771年摹刻的《大唐中兴颂》,因元结的“文绝”,颜真卿的“字绝”,摩崖石刻的“石绝”,誉称“摩崖三绝”,该碑高3米,宽3.2米,碑身离地有3.7米(如图所示),有一身高为的游客从正面观赏它(该游客头顶T到眼睛C的距离为),设该游客离墙距离为x米,视角为,为使观赏视角最大,x应为( )
A. B.3 C. D.
11.如图所示,将一副三角板拼成平面四边形,将等腰直角沿向上翻折,得到,设,点分别为棱的中点,为线段上的动点,下列说法错误的是( )
A.在翻折过程中,存在某个位置使得
B.若,则与平面所成角的正切值为
C.三棱锥体积的最大值为
D.当时,的最小值为
12.在单位正方体内任取一个点,过这个点作三个平行于正方体面的平面,将正方体分成个小长方体,则这些小长方体中体积不大于的长方体的个数的最小值是( )
A. B. C. D.
二、填空题
13.在正方体中,二面角的平面角等于 .
14.已知向量.若,则 .
15.已知圆锥的侧面积为,且它的侧面展开图是一个半圆,则这个圆锥的底面半径是 .
16.如图,在正方体中,是棱的中点,记平面与平面的交线为,平面与平面的交线为,若直线分别与,所成的角为 , ,则 , .
17.已知正四面体中,分别在棱上. 若, ,则 .
18.球面三角学是研究球面三角形的边、角关系的一门学科.如图,球的半径为R,A,B,为球面上三点,劣弧BC的弧长记为,设表示以为圆心,且过B,C的圆,同理,圆的劣弧的弧长分别记为,曲面(阴影部分)叫做曲面三角形,,则称其为曲面等边三角形,线段OA,OB,OC与曲面围成的封闭几何体叫做球面三棱锥,记为球面.设.
①若平面是面积为的等边三角形,则;
②若,则;
③若平面为直角三角形,且,则;
④若,则球面的体积;
其中所有正确结论的序号是 .
三、解答题
19.已知函数.
(1)求的最小正周期和单调递增区间;
(2)若,求的最大值和最小值及取得最值时相应的值.
20.如图,在四棱锥中,底面为矩形,平面平面,,,、分别为、的中点.
(Ⅰ)求证:;
(Ⅱ)求证:平面平面;
(Ⅲ)求证:平面.
21.已知的面积为,再从条件①、条件②这两个条件中选择一个作为已知,求:
(1)和的值;
(2)的值.
条件①:,;条件②:,.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
22.如图所示,在三棱柱中,侧棱底面,为棱的中点.,, .
(1)求证:平面;
(2)求证:平面;
(3)在棱上是否存在点,使得平面平面?如果存在,求此时的值;如果不存在,请说明理由.
23.对于n行n列()的数表,定义T变换:任选一组,其中,,对于A中第行和第j列个数,将每个数同时加1,或者将每个数同时减1,其余的数不变,得到一个新数表.
(1)已知对依次进行4次T变换,如下:,写出a,b,c,d的值.
(2)已知,,那么是否可以依次进行有限次T变换,将A变换为B?说明理由.
(3)已知11行11列的数表,那么是否可以依次进行k次T变换,将其变换为?若可以,求k的最小值;若不可以,说明理由.
参考答案
1.【答案】D
【详解】
如图,在正方体中分析选项A、B、C.
A.平面,平面,平面平面,但,A错误.
B.,平面,但平面,B错误.
C.平面平面,平面,,但平面,C错误.
D.取直线的方向向量,直线的方向向量,
∵,,∴分别为平面的法向量,
∵,∴,∴,D正确.
故选D.
2.【答案】B
【详解】由题可知球直径为长方体的体对角线,故半径为,
.
故选B.
3.【答案】D
【详解】对于A,如下图所示,
易得,
则,
又平面,平面,
则平面,故A满足;
对于B,如下图所示,
为所在棱的中点,连接,
易得,
则四边形为平行四边形,
四点共面,
又易知,
又平面,平面,
则平面,故B满足;
对于C,如下图所示,
点为所在棱的中点,连接,
易得四边形为平行四边形,四点共面,
且,
又平面,平面,
则平面,故C满足;
对于D,连接,
由条件及正方体的性质可知四边形是等腰梯形,
所以与所在的直线相交,
故不能推出与平面不平行,故D不满足,
故选D.
4.【答案】B
【详解】设,
由题意可得,则,
所以,
所以在中,,
由,所以,即中最长的边长为.
故选B
5.【答案】C
【详解】化简得,
,
,,
,
故选:C.
6.【答案】A
【分析】先判断如果能不能推出是钝角三角形,再判断如果是钝角三角形,是否一定有即可.
【详解】如果,由于B是三角形的内角,并且,则,
即,是钝角三角形,
所以“”是“是钝角三角形”的充分条件;
如果是钝角三角形,不妨设,则,
所以“”不是“是钝角三角形”的必要条件.
故选A.
【方法总结】充分必要条件和对应集合的关系可根据如下规则转化:
若p是q的必要不充分条件,则q对应集合是p对应集合的真子集;
若p是q的充分不必要条件,则p对应集合是q对应集合的真子集;
(3)若p是q的充要条件,则p对应集合与q对应集合相等;
(4)若p是q的既不充分也不必要条件,则q对应集合与p对应集合互不包含.
7.【答案】D
【详解】如图,连接,因为∥,
所以或其补角为直线与所成的角,
因为平面,所以,又,,
所以平面,所以,
设正方体棱长为2,则,
,所以.
故选D
8.【答案】D
【详解】设容器底面半径为,倒置前液面的半径为,倒置后液面的半径为
则,
则水的体积为,
倒置后水的体积,
所以,
故选D
9.【答案】A
【详解】由题意,若,则棱与平面交于点,符合题意,此时;
若,,则棱与平面交于线段,符合题意,此时.
排除B、C、D选项.
故选A.
10.【答案】A
【详解】设,由图可知,
,
由基本不等式知,当,即时,最大,从而角最大.
故选A
11.【答案】D
【详解】对于A,当平面与平面垂直时,
,平面与平面的交线为,平面,
平面,又平面,
,,故A正确;
对于B,连接,
因为平面,
所以平面,
又平面,所以,
因为为的中点,
所以,
又平面,
所以平面,
则即为与平面所成角的平面角,
在中,,则,
,
所以,
即与平面所成角的正切值为,故B正确;
对于C,三棱锥的体积(为点到平面的距离).
.
当平面平面时,最大,的最大值为,此时,所以三棱锥体积的最大值为,选项C正确.
对于D,当时,因为为的中点,
所以,则,
又因为的中点,所以,
又,所以,
所以,
如图将沿旋转,使其与在同一平面内,
则当三点共线时,最小,
即的最小值为,
在中,,
则,
所以,
所以的最小值为,故D错误.
故选D.
12.【答案】B
【详解】设该正方体的长宽高分别被切成长度为和,和,和的两段,
设,且根据据对称性,可不妨设,
此时,8个长方体的体积分别是
由,可知,
因为,
所以,
又因为,
所以和中至少有一个数不超过,
所以这8个长方体中至少有4个的体积不超过.
当时,8个长方体的体积分别是0.0625;0.061875;0.061875;0.075625;0.151875;0.185625;0.185625;0.226875;
此时这8个长方体中恰有4个的体积不超过.
综上,这些小长方体中体积不大于的长方体个数的最小值为4.
故选:B.
13.【答案】
【详解】
在正方体中,面,面,
所以,因为,,平面,
所以平面,平面,所以,
所以二面角的平面角为,在正方体中易知.
14.【答案】.
【详解】,
,解得.
15.【答案】1
【详解】设圆锥的底面半径为r,圆锥的母线长为l,则,解得:,又,解得:.
16.【答案】;
【解析】本题考查等角定理及其辨析、面面平行
在正方体中,是棱的中点,
如图,延长与延长线交于点,连接,则直线即为直线,,
由,得,又,于是,
由平面平面,平面 平面,平面 平面,
则,又,因此,,
所以.
17.【答案】3或
【详解】
当时,是等边三角形,因此.
在中,由余弦定理可得,
则,解得.
当时,不妨设.
在中分别使用余弦定理可得
由可知是关于的方程的两个相异正实根,
所以
可写为,因此,解得.
即.
18.【答案】①②④
【详解】对于①,因等边三角形的面积为,则,
又,故,则,故①正确;
对于②,由可得,故,即②正确;
对于③,由余弦定理可知,由可得,,
即,化简得,.
取,则,则,故③错误;
对于④,由可得,故,
由正弦定理,的外接圆半径为,点到平面ABC的距离,
则三棱锥的体积,
而球面的体积,故④正确.
19.【答案】(1)最小正周期为,增区间为
(2)当时,,当时,
【详解】(1)函数
,
所以函数的最小正周期为,
由可得,
所以函数的增区间为.
(2)当时,,
故当时,即当时,取最小值,即;
当时,即当时,取最大值,即.
20.【答案】(Ⅰ)见解析;(Ⅱ)见解析;(Ⅲ)见解析.
【详解】(Ⅰ)∵,且为的中点,∴.
∵底面为矩形,∴,∴;
(Ⅱ)∵底面为矩形,∴.
∵平面平面,平面平面,平面,
∴平面,又平面,∴.
又,,、平面,平面,
∵平面,∴平面平面;
(Ⅲ)如图,取中点,连接.
∵分别为和的中点,∴,且.
∵四边形为矩形,且为的中点,∴,
∴,且,∴四边形为平行四边形,
∴,又平面,平面,∴平面.
21.【答案】(1)条件选择,答案见解析;
(2)条件选择,答案见解析.
【详解】(1)选①,在中,由得:,而,
则面积,解得,
由余弦定理得:,
所以,.
选②,在中,由得:,而,即,
则面积,解得,
由余弦定理得:,
所以,.
(2)选①,由(1)及正弦定理得:,则,
,而角为钝角,于是得,
所以.
选②,由(1)知,,
所以.
22.【答案】(1)证明见解析;
(2)证明见解析;
(3)存在,.
【详解】(1)连结交于O,连结
在中,因为M,O分别为AC,中点,所以
又因为平面,平面,所以平面
(2)因为侧棱底面ABC,平面ABC,所以
又M为棱AC中点,,所以
因为,,平面
所以平面,平面,所以
因为M为棱AC中点,,所以,又,
所以在和中,
所以,即,所以
因为,BM,平面,所以平面
(3)当点N为中点时,即,平面平面
设中点为D,连结DM,
因为D,M分别为,AC中点,所以,且
又因为N为中点,所以,且,
所以四边形DMBN是平行四边形,所以,
结合(2)平面,则平面,
又平面,所以平面平面
23.【答案】(1),
(2)不可以,理由见解析
(3)可以,k的最小值为400
【详解】(1)经过变换得到,显然没有变,从1变为2,
所以和均增加1,故,
经过变换得到,显然没有变,从1变为2,
故和均增加1,故,
经过变换得到,满足要求,
综上,,;
(2)不可以,理由如下:
由题可知,每次变换,数表中的所有数的和增加或减少5,
因为中所有数的和为0,所以经过有限次T变换后,各数之和应为5的倍数,
而中所有数的和为9,不合要求,
故不可以依次进行有限次T变换,将A变换为B.
(3)可以,且的最小值为400,
当所选时,所有加1的变换与减1的变换次数之差设为,
当所选且,或者且时,
所有加1的变换与减1的变换次数之差设为,
当所选时,加1的变换与减1的变换次数之差设为,
由于,
由于,,和为100,故,
由于或时,,和为,
故,
由于,故,
联立可得,解得,
所以,
其中符合题意的400次变换构造如下:
当所选时,各进行一次减1的变换,共进行100次变换,得到
当所选且,或者且时,
各进行10次加1的变换,共进行200次变换,得到
当所选时,进行100次减1的变换,得到
同课章节目录
