山东省潍坊市诸城市第一中学2024-2025学年高一下学期诊断考试模拟数学试题(含答案)
文档属性
| 名称 | 山东省潍坊市诸城市第一中学2024-2025学年高一下学期诊断考试模拟数学试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-09 00:00:00 | ||
图片预览



文档简介
高一下学期数学诊断拟试题
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.若则的大小关系是
A. B.
C. D.
2.设是第二象限角,为其终边上一点,且,则
A. B. C. D.
3.要得到函数 的图象,只需将函数 的图象
A.向左平移2个单位长度 B.向右平移π/2个单位长度
C.向右平移2个单位长度 D.向左平移π/2个单位长度
4.若向量,满足||=||=3,且则向量在向量上的投影向量是
C. D.
若函数 在 ]上单调递增,则ω的最大值是
A. B.1 C.2 D.3
6.“七巧板”是我国古代劳动人民的伟大发明,被誉为“东方魔方”.某同学制作了一个“七巧板”玩具,如图所示.其中正方形ABCD的边长为4,点E,O,N分别是线段AB,AC,OC的中点,则
A.-20 B.-14 C.20 D.14
7.已知向量=(1,0),且·=2,·=-3,则|-|的最小值是
A.3 B.4 C.5 D.6
已知A,B 是直线与函数f(x)=2sin(ωx+φ)(ω>0)图象的两个相邻交点,且
|AB| 则ω= A.2 B.4 C.2或6 D.4或8
选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.关于非零向量,,向量,的夹角为,下列说法正确的是( )
B.在向量上的投影向量为
C.若则ā与b的夹角为钝角
10.已知函数f(x)=2sin(x+φ)+ sinx+1的最小值为 ,则φ的值可能是
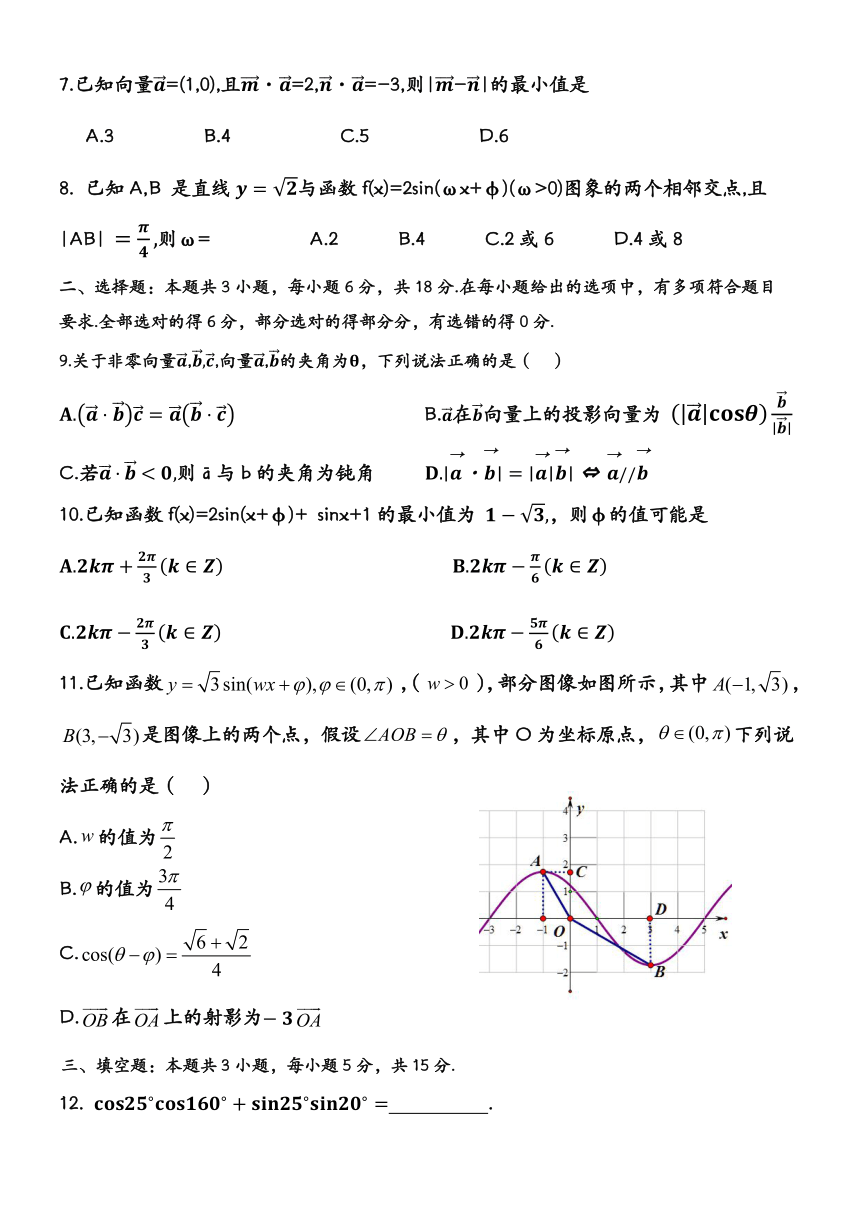
11.已知函数,(),部分图像如图所示,其中,是图像上的两个点,假设,其中O为坐标原点,下列说法正确的是( )
A.的值为
B.的值为
C.
D.在上的射影为
三、填空题:本题共3小题,每小题5分,共15分.
12. .
13.已知,,是函数的两个零点,且的最小值为,若将函数的图象向左平移个单位长度后得到的图象关于对称,则的最大值为 .
14.已知函数 图象经过点(0,l), 若f(x)在 上有且只有两个最值点,则实数ω的取值范围是 .
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(本题满分13分)
设向量,满足 且(3-2)·(5+4)=1.
(1)求向量,的夹角; (2)若 求t 的值.
16.(本题满分15分)
已知 且
(1)求 cosθ的值; (2)求 tanθ的值; (3)求 的值
17.(本题满分15分)某同学用“五点法”画函数 在某一个周期内的图象时,列表并填入了部分数据,如下表:
x
0
0 3 0 0
(1)请将上表数据补充完整,并写出函数的解析式(直接写出结果即可);
(2)根据表格中的数据作出在一个周期内的图象;
(3)将函数图像上所有点的横坐标变为原来的倍,纵坐标变为原来的2倍,再将所得函数图像上所有点向左平移个单位长度得到g(x)的图像,求g(x)的在区间 上的值域.
18.(17分)
如图,在直角梯形ABCD 中,AD⊥AB,AD=CD=4,AB=6,E是线段AB 的中点,F 在线段 BC上(不包含端点),线段AF,DE 相交于点 P.
(1)若 F 是线段BC 的中点,求 的值;
(2)若 求 的值;
(3)若 求 的值.
19.(17分)
若函数,则称为向量a,b的点积函数.例如:向量=(2,x),=(cosx, 则向量,的点积函数=2cosx-x.
(1)若向量=(1,-1),=(acosx, bsinx)(a,b∈R),且向量,的点积函数=2cosx+2sinx,求||的值;
(2)若向量 求向量,的点积函数g(x)的值域、
(3)若向量 的点积函数为h(x),且存在 使得-2≤h(x)+k≤3成立,求k 的取值范围.
高一下学期数学诊断模拟试题答案
单选题DDADCDCC 二、多选题9.BD 10. AC 11. BCD
三、填空题12. 13. 14.(10.16]
四、解答题
15.解:(1)因为(3a-2b)·(5a+4b)=1,所以 …………2分
因为 所以15+2a·b-8×2=1,所以a·b=1, … 4分
则 ……… 5分
故 即向量a,b的夹角为 … 7 分
(2)因为 所以( 即 … 9分
因为 且a·b=1,所以 即 … 11分
解得t=-3或t=1 ...........13分
16.解:(1)因为,所以,所以,
且.................3分
所以...5分
(2)由(1)得:.........7分
所以...................10分
(3)因为,,
,...........12分
所以:..........15分
17(1)由题可知,,所以,.........2分
,,..........4分
,.................5分
则数据补全如下表:
0
0 3 0 0
.............................................................................................7分
(2)由(1),在一个周期内的图象如图所示,
;.........................................10分
(3),................12分
当时,,.......................13分
则,则,
即在区间上的值域为..........................15分
18.(1)以点为坐标原点,分别以为轴,为轴建立平面直角坐标系,
则、、、,则,...........2分
则,
所以...................4分
(2)设,
则,,
若,则,
解得,..................7分
所以,故................9分
(3)设,
由三点共线可得:.......11分
所以...........13分
由,
可得,
所以,即,解得..........................15分
所以......................17分
19.(1)由题意,,
则,即..............2分
所以....................4分.
(2)由题意,......6分
令,
则,对称轴为,
则函数在上单调递增,
当,,
则的值域为..................10分
(3)由题意,
.......................12分
由,得,则,
则,即..................14分
则,
由于存在,使得成立,
则,解得,
即的取值范围为......................17分
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.若则的大小关系是
A. B.
C. D.
2.设是第二象限角,为其终边上一点,且,则
A. B. C. D.
3.要得到函数 的图象,只需将函数 的图象
A.向左平移2个单位长度 B.向右平移π/2个单位长度
C.向右平移2个单位长度 D.向左平移π/2个单位长度
4.若向量,满足||=||=3,且则向量在向量上的投影向量是
C. D.
若函数 在 ]上单调递增,则ω的最大值是
A. B.1 C.2 D.3
6.“七巧板”是我国古代劳动人民的伟大发明,被誉为“东方魔方”.某同学制作了一个“七巧板”玩具,如图所示.其中正方形ABCD的边长为4,点E,O,N分别是线段AB,AC,OC的中点,则
A.-20 B.-14 C.20 D.14
7.已知向量=(1,0),且·=2,·=-3,则|-|的最小值是
A.3 B.4 C.5 D.6
已知A,B 是直线与函数f(x)=2sin(ωx+φ)(ω>0)图象的两个相邻交点,且
|AB| 则ω= A.2 B.4 C.2或6 D.4或8
选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.关于非零向量,,向量,的夹角为,下列说法正确的是( )
B.在向量上的投影向量为
C.若则ā与b的夹角为钝角
10.已知函数f(x)=2sin(x+φ)+ sinx+1的最小值为 ,则φ的值可能是
11.已知函数,(),部分图像如图所示,其中,是图像上的两个点,假设,其中O为坐标原点,下列说法正确的是( )
A.的值为
B.的值为
C.
D.在上的射影为
三、填空题:本题共3小题,每小题5分,共15分.
12. .
13.已知,,是函数的两个零点,且的最小值为,若将函数的图象向左平移个单位长度后得到的图象关于对称,则的最大值为 .
14.已知函数 图象经过点(0,l), 若f(x)在 上有且只有两个最值点,则实数ω的取值范围是 .
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(本题满分13分)
设向量,满足 且(3-2)·(5+4)=1.
(1)求向量,的夹角; (2)若 求t 的值.
16.(本题满分15分)
已知 且
(1)求 cosθ的值; (2)求 tanθ的值; (3)求 的值
17.(本题满分15分)某同学用“五点法”画函数 在某一个周期内的图象时,列表并填入了部分数据,如下表:
x
0
0 3 0 0
(1)请将上表数据补充完整,并写出函数的解析式(直接写出结果即可);
(2)根据表格中的数据作出在一个周期内的图象;
(3)将函数图像上所有点的横坐标变为原来的倍,纵坐标变为原来的2倍,再将所得函数图像上所有点向左平移个单位长度得到g(x)的图像,求g(x)的在区间 上的值域.
18.(17分)
如图,在直角梯形ABCD 中,AD⊥AB,AD=CD=4,AB=6,E是线段AB 的中点,F 在线段 BC上(不包含端点),线段AF,DE 相交于点 P.
(1)若 F 是线段BC 的中点,求 的值;
(2)若 求 的值;
(3)若 求 的值.
19.(17分)
若函数,则称为向量a,b的点积函数.例如:向量=(2,x),=(cosx, 则向量,的点积函数=2cosx-x.
(1)若向量=(1,-1),=(acosx, bsinx)(a,b∈R),且向量,的点积函数=2cosx+2sinx,求||的值;
(2)若向量 求向量,的点积函数g(x)的值域、
(3)若向量 的点积函数为h(x),且存在 使得-2≤h(x)+k≤3成立,求k 的取值范围.
高一下学期数学诊断模拟试题答案
单选题DDADCDCC 二、多选题9.BD 10. AC 11. BCD
三、填空题12. 13. 14.(10.16]
四、解答题
15.解:(1)因为(3a-2b)·(5a+4b)=1,所以 …………2分
因为 所以15+2a·b-8×2=1,所以a·b=1, … 4分
则 ……… 5分
故 即向量a,b的夹角为 … 7 分
(2)因为 所以( 即 … 9分
因为 且a·b=1,所以 即 … 11分
解得t=-3或t=1 ...........13分
16.解:(1)因为,所以,所以,
且.................3分
所以...5分
(2)由(1)得:.........7分
所以...................10分
(3)因为,,
,...........12分
所以:..........15分
17(1)由题可知,,所以,.........2分
,,..........4分
,.................5分
则数据补全如下表:
0
0 3 0 0
.............................................................................................7分
(2)由(1),在一个周期内的图象如图所示,
;.........................................10分
(3),................12分
当时,,.......................13分
则,则,
即在区间上的值域为..........................15分
18.(1)以点为坐标原点,分别以为轴,为轴建立平面直角坐标系,
则、、、,则,...........2分
则,
所以...................4分
(2)设,
则,,
若,则,
解得,..................7分
所以,故................9分
(3)设,
由三点共线可得:.......11分
所以...........13分
由,
可得,
所以,即,解得..........................15分
所以......................17分
19.(1)由题意,,
则,即..............2分
所以....................4分.
(2)由题意,......6分
令,
则,对称轴为,
则函数在上单调递增,
当,,
则的值域为..................10分
(3)由题意,
.......................12分
由,得,则,
则,即..................14分
则,
由于存在,使得成立,
则,解得,
即的取值范围为......................17分
同课章节目录
